Эквивалентность инвариантной массы и энергии покоя. Знаменитая формула Эйнштейна. Вспомним обычные определения энергии и импульса из школьного курса, которые используются в не релятивисте кой механике Ньютона. Энергия обычно разделяется на потенциальную и кинетическую. Потенциальная определяется высотой тела над поверхностью Земли. Её исключим из рассмотрения, предполагая, что нет гравитационного поля Земли. Кинетическая энергия определяется массой и скоростью тела:

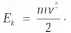
Импульс определяется простой формулой р = mv, m — инвариантная относительно преобразований инерциальная масса тела, масса покоя. Как изменятся эти величины при переходе к другой инерциальной системе? В рамках преобразований Галилея нужно лишь заменить скорость тела ν на ν' = ν + V, где V — скорость движения одной системы относительно другой.

В специальной теории относительности мы имеем дело с релятивистской механикой. В её рамках энергия движущегося тела и его импульс выражаются формулами:

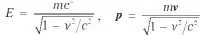
Как релятивистские энергия и импульс преобразуются при переходе от одной инерциальной системы к другой? Ответ простой: с помощью преобразований Лоренца. Релятивистские энергию и компоненты импульса (для сохранения размерности — cp) можно мыслить, как компоненты единого 4–х вектора в пространстве Минковского, который называют вектором энергии–импульса. Строим квадрат длины этого 4–мер но го вектора точно так же, как был построен квадрат интервала между событиями Как и интервал, эта величина инвариантна относительно поворотов Лоренца и всегда имеет значение:

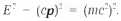
Знак минус и здесь отражает тот факт, что пространство Минковского — псевдоевклидово. Легко видеть, если частица покоится и р = 0, то её полная энергия выражается знаменитой формулой: Е = тс². Это согласуется с релятивистским выражением для энергии, если там положить ν = 0, и приводит к выводу, что вся масса покоя тела может быть превращена в энергию, а энергия может обращаться в массу покоя.

Представим релятивистские энергию и импульс для малых скоростей ν: они переходят в не релятивисте кие Е = mc²- + Е_k (где второе слагаемое — обычная кинетическая энергия, она определена выше) и р = mν. Как видим, здесь не релятивистская энергия отличается от кинетической энергии Ньютона на величину, которую мы уже назвали энергией покоя. То есть в СТО у массивных частиц состояний с нулевой энергией не бывает.

Кроме этих выводов, сделаем ещё один: в СТО естественным образом описываются частицы с нулевой массой покоя m = 0, такие как фотон, для них E² = (cp)². Очевидно, что в пространстве Минковкого они распространяются со скоростью света. Действительно, длина 4–вектора энергии–импульса для них равна нулю, т. е. их мировые линии лежат на световом конусе.

«Утяжеление релятивистской массы». Иногда в литературе, особенно часто — в популярной, встречается понятие «релятивисткой массы», Откуда оно взялось? В выражениях для релятивистских энергии и импульса инвариантную массу покоя можно заменить выражением:

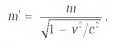
Эта величина и называется релятивистской массой. Тогда релятивистская энергия приобретает форму формулы Эйнштейна Е=m'c², а релятивистский импульс форму обычного импульса p = m'ν. Ясно, что с возрастанием скорости ν, величина m' увеличивается, а при ν = c обращается в бесконечность Возможно, это выглядит как яркий пример в популярной литературе. Но исследователи, как правило, этой величиной не оперируют, чтобы не создавать путаницы, ведь релятивистские энергия и импульс ведут себя точно так же. Действительно, они растут с увеличением скорости, Но для реальных тел ни энергия, ни импульс не могут достигать бесконечных значений. Это значит, что объекты с ненулевой массой покоя не могут достичь скорости света, а их траектория всегда находится внутри светового конуса. Куда удобнее использовать массу покоя, которая является инвариантной величиной.