4. Альтернативные истории
В 1999 году группа австрийских физиков провела эксперимент по обстрелу некой преграды серией молекул, структура которых напоминает рисунок на поверхности футбольного мяча. Эти молекулы, из шестидесяти атомов углерода каждая, иногда называют бакиболами или фуллеренами — в честь американского архитектора Бакминстера Фуллера (1895–1983), который строил здания подобной конструкции. Так называемые геодезические купола Фуллера представляют собой, пожалуй, крупнейшие объекты со структурой футбольного мяча. Бакиболы же — наименьшие из таких объектов. В преграде, на которую ученые их направили, имелось две щели, сквозь которые бакиболы могли пролететь. Позади преграды физики расположили своего рода экран для обнаружения и подсчета проскочивших молекул.
Бакиболы. Бакиболы похожи на микроскопические футбольные мячи, состоящие из атомов углерода.
Если мы поставим аналогичный эксперимент с настоящими футбольными мячами, нам понадобится игрок — не особенно меткий, но способный весьма продолжительное время бить по возникающим перед ним мячам с заданной нами скоростью. Мы расположим этого игрока перед преградой — стенкой, в которой имеется два вертикальных проема. Позади стенки (параллельно ей) натянем очень длинную сетку. Большинство посланных игроком мячей попадет в преграду и отскочит обратно, но некоторые пролетят сквозь тот или другой проем и попадут в сетку. Если проемы будут лишь чуточку больше мяча, то по другую сторону стенки-преграды возникнут два строго параллельных потока. Если же проемы немного расширить, каждый из потоков будет слегка расходиться (см. ил., с. 72).

Футбол через стенку-преграду с двумя проемами. Когда футболист посылает мячи через проемы в стенке, мы можем наблюдать обычную картину.
Если мы закроем один из проемов, то соответствующий ему поток мячей не сможет пролетать через преграду, однако это никак не повлияет на другой поток. Если мы снова откроем тот проем, который был закрыт, это лишь увеличит число мячей, приземлившихся в любой избранной точке по другую сторону стенки, поскольку это будут все мячи, прошедшие через остававшийся открытым проем, плюс другие мячи, прошедшие через вновь открытый проем. Иными словами, если одновременно открыть два проема, мы увидим сумму тех мячей, которая появилась бы за преградой в том случае, когда мы открывали бы поочередно каждый из проемов. Такова реальность, к которой мы привыкли в повседневной жизни. Совсем иную картину увидели австрийские исследователи, когда вели обстрел своими молекулами.
В австрийском эксперименте открытие второго проема действительно увеличивало число молекул, попадавших на определенный участок экрана, но при этом уменьшало их число на другом участке (см. ил., с. 73).

Бакибольный футбол через двухщелевую преграду. Когда молекулы-«мячи» пролетают сквозь щели, на экране появляется узор, соответствующий какому-то квантовому закону.
Фактически были точки, куда бакиболы вообще не попадали, когда были открыты обе щели, но они попадали туда, если открытой оставалась лишь одна из щелей. Это должно выглядеть весьма странным. Как может открытие второй щели уменьшить число молекул, попадающих в определенную точку?
Чтобы получить ключ к ответу, изучим всё детально. В этом эксперименте многие из молекулярных «мячей» попали в пятно, центр которого располагался на полпути между теми местами, куда можно было ожидать попадания мячей, пролетевших через ту и другую щели. В места, расположенные чуть дальше от этой центральной точки, попадало очень мало молекул, но еще чуть дальше снова наблюдалось скопление молекул, прошедших через щель. Этот узор не является суммой узоров, полученных, когда каждая щель открывалась отдельно, но он напоминает картину, характерную для интерферирующих волн, показанную на иллюстрации в главе 3. Участки, куда молекулы не попадали, соответствуют областям, в которые волны, исходящие из двух щелей, приходили в противофазе и создавали деструктивную интерференцию; участки же, куда попадало много молекул, соответствовали областям, которых волны достигали в одинаковой фазе и создавали конструктивную интерференцию.
В течение первых двух тысяч лет развития научной мысли основой для теоретических объяснений служили повседневный опыт и интуиция. По мере того как мы развивали технические устройства и расширяли с их помощью диапазон явлений, доступных нашим наблюдениям, мы стали замечать, что поведение природы все меньше и меньше соответствует нашему повседневному опыту и нашей интуиции, о чем, например, свидетельствует эксперимент с бакиболами. Этот эксперимент типичен для явлений, которые не может объяснить классическая наука, но которые описываются квантовой физикой. Ричард Фейнман считал, что эксперимент с использованием преграды с двумя щелями, подобный описанному выше, «заключает в себе всю тайну квантовой механики».
Принципы квантовой физики были разработаны в первые десятилетия XX века, после того как теорию Ньютона сочли недостаточной для описания природы на атомном и субатомном уровнях. Фундаментальные физические теории описывают силы природы и то, как объекты реагируют на них. Классические теории, такие как теория Ньютона, построены на основе повседневного опыта, где материальные объекты существуют индивидуально, могут располагаться в определенных местах, следуют строго определенным траекториям и т. д. Квантовая физика дает основу для понимания того, как природа действует на атомном и субатомном уровнях, но, как мы расскажем более подробно в дальнейшем, она диктует совершенно иную концептуальную схему — такую, в которой положение объекта, его путь и даже его прошлое и будущее точно не определены. Квантовые теории таких сил, как гравитационная или электромагнитная, построены именно на этой основе.
Могут ли теории, построенные на основе, столь чуждой повседневному опыту, объяснить присущие ему явления, которые столь точно были смоделированы классической физикой?
Оказывается, могут, поскольку и мы, и всё, что нас окружает, это составные объекты, то есть структуры, состоящие из невообразимо большого количества атомов, — этих атомов больше, чем звезд в обозримой части Вселенной. И хотя все эти атомы подчиняются принципам квантовой физики, можно продемонстрировать, что их крупные совокупности, слагающие футбольные мячи, морковки, аэробусы и нас самих, конечно же сумеют избежать дифракции при прохождении через проемы. Поэтому, хотя компоненты обычных объектов и подчиняются квантовой физике, законы Ньютона представляют собой эффективную теорию, которая с высокой точностью описывает поведение сложных структур, образующих наш повседневный мир.
Это может показаться странным, но в науке есть много случаев, когда поведение крупного образования выглядит отличающимся от поведения его индивидуальных компонентов. Реакции одного нейрона едва ли такие же, как у человеческого мозга в целом, а знание свойств молекулы воды вряд ли много расскажет вам о поведении озера. В случае квантовой физики ученые и по сей день работают над тем, чтобы подробно выяснить, как законы Ньютона проистекают из квантовой области. Нам известно лишь, что составляющие элементы всех объектов подчиняются законам квантовой физики, а законы Ньютона представляют собой хорошее приближение для того, чтобы описать, как ведут себя макроскопические объекты, состоящие из таких квантовых компонентов.
Именно поэтому прогнозы теории Ньютона совпадают с нашим видением реальности, которое мы все развиваем по мере знакомства с окружающим миром. Но образ действия отдельных атомов и молекул кардинально отличается от того, с которым мы сталкиваемся в повседневной жизни. Квантовая физика представляет собой новую модель реальности, дающую нам иную картину Вселенной. Это картина, в которой многие понятия, основополагающие для нашего интуитивного понимания реальности, больше не имеют значения.
Впервые эксперимент с двухщелевой преградой провели в 1927 году американские физики-экспериментаторы Клинтон Дэвиссон (1881–1958) и Лестер Джермер (1896–1971) из компании «Белл Лабз». Они изучали, как пучок электронов — объектов, которые гораздо проще, чем бакиболы, — взаимодействует с кристаллом никеля. То, что материальные частицы, электроны, ведут себя подобно волнам на воде, оказалось поразительным экспериментом, который вдохновил квантовую физику. Поскольку на макроскопическом уровне такое поведение не наблюдалось, ученые долго не могли понять, насколько большим и сложным должно быть нечто, чтобы оно все еще продолжало проявлять подобные волновые свойства. Если бы эффект удалось продемонстрировать, используя людей или гиппопотамов, это вызвало бы настоящую сенсацию, но, как мы уже сказали, чем больше объект, тем, как правило, менее очевидными и менее устойчивыми становятся квантовые эффекты. Поэтому вряд ли какое-нибудь животное в зоопарке сможет пройти, подобно волне, сквозь железные прутья клетки. И все же физики-экспериментаторы стали наблюдать волновые свойства у все более крупных «частиц». Ученые надеются когда-нибудь повторить эксперимент с бакиболами, используя вирус, который не только гораздо больше по размерам, но и рассматривается некоторыми как живое существо.
Есть всего несколько аспектов квантовой физики, необходимых для того, чтобы понять рассуждения, которые мы приведем в последующих главах. Одна из основных особенностей — двойственная природа (дуализм) волны-частицы. То, что материальная частица ведет себя подобно волне, удивило всех. То, что свет ведет себя как волна, уже не удивляет никого. Волноподобное поведение света кажется нам естественным и считается общепринятым фактом на протяжении уже почти двух веков. Если в упомянутом выше эксперименте направить луч света на две щели, то появятся две волны, которые и встретятся на экране. В каких-то точках их гребни или впадины совпадут, образовав яркое пятно, а в других местах гребни одной волны наложатся на впадины другой, поглотив их и образовав темный участок. В начале XIX века английский физик Томас Юнг (1773–1829) провел этот эксперимент (известный теперь как опыт Юнга) и убедил всех, что свет — это волна и он не состоит из частиц, как считал Ньютон.
Хотя некоторые могли сделать вывод, что Ньютон был не прав, говоря, что свет — это не волна, но все же он был прав, говоря, что свет может действовать так, как если бы он состоял из частиц. Сегодня мы называем эти частицы фотонами. Как мы состоим из большого числа атомов, так и свет, который мы видим в повседневной жизни, состоит из великого множества фотонов, — даже одноваттный ночник излучает миллиард миллиардов фотонов в секунду. Одиночные фотоны обычно незаметны, но в лаборатории можно создать весьма слабый луч света, состоящий из потока одиночных фотонов, которые мы сможем обнаруживать индивидуально, точно так же, как мы обнаруживаем одиночные электроны или бакиболы. И мы можем повторить опыт Юнга, используя настолько разреженный луч, что фотоны будут достигать преграды поодиночке, с интервалом в несколько секунд. Если мы сделаем это, а потом сложим все отдельные попадания, зафиксированные на расположенном за преградой экране, то обнаружим, что вместе они создают точно такой же интерференционный узор, какой возник бы в том случае, если бы мы провели опыт Дэвиссона — Джермера, но обстреливали бы экран электронами (или бакиболами) поштучно. Для физиков это было потрясающим открытием: если отдельные частицы интерферируют сами с собой, то волновая природа света является свойством не только луча, или большого скопления фотонов, но и отдельной частицы.

Опыт Юнга. Узор, возникающий в эксперименте с бакиболами, был известен из волновой теории света.
Еще одним из основных принципов квантовой физики является принцип неопределенности, который в 1926 году сформулировал немецкий физик Вернер Гейзенберг (1901–1976). Принцип неопределенности говорит о том, что существуют пределы наших возможностей одновременного измерения определенных величин, таких как положение и скорость частицы. Например, согласно принципу неопределенности, если вы умножаете неопределенность положения частицы на неопределенность ее импульса (произведения массы на скорость), то результат не может бьггь меньше некой фиксированной величины, которую называют постоянной Планка. Это звучит как сложная скороговорка, но суть ее может быть выражена просто: чем точнее вы измеряете скорость, тем менее точно можете измерить положение, и наоборот. Например, если вы вдвое уменьшаете неопределенность положения, то вам придется вдвое увеличить неопределенность скорости. Также важно отметить, что по сравнению с обычными единицами измерения, такими как метры, килограммы и секунды, постоянная Планка очень мала. Действительно, если выразить ее в этих единицах, то значение составит примерно 6/10 000 000 000 000 000 000 000 000 000 000 000. В результате, если вы засечете местоположение макроскопического объекта, например футбольного мяча массой в треть килограмма, с точностью до одного миллиметра в каждом направлении, мы все еще сможем измерить его скорость с точностью гораздо большей, чем одна миллиардная миллиардной от одной миллиардной километра в час. Это потому, что измеренная в таких единицах масса футбольного мяча равна 1/3, а неопределенность положения 1/1000. Ни того ни другого не достаточно, чтобы привести ко множеству нулей в постоянной Планка, так что эта роль достается неопределенности в скорости. Но в тех же единицах масса электрона составляет 0,000 000 000 000 000 000 000 000 000 001, поэтому с электронами дело обстоит совершенно по-другому. Если мы измеряем положение электрона с точностью, примерно соответствующей размеру атома, то принцип неопределенности устанавливает, что мы не можем узнать скорость электрона более точно, чем примерно плюс-минус 1000 километров в секунду, что уж никак не назовешь очень точным.

«Если это действительно так, то все, что мы принимали за волну, на самом деле было частицей, а все, что мы принимали за частицу, было волной».
Согласно квантовой физике, независимо от того, сколько информации мы получаем или сколь велики наши вычислительные способности, результаты физических процессов не могут быть предсказаны однозначно, потому что они не имеют однозначной определенности. Наоборот, учитывая данное начальное состояние системы, Природа определяет свое будущее состояние посредством процесса, который существенно неоднозначен. Иными словами, Природа не диктует результат какого-либо процесса или эксперимента даже в простейших ситуациях. Скорее, она предоставляет много различных возможностей, каждая из которых может реализоваться с той или иной степенью вероятности. Это, перефразируя Эйнштейна, как если бы Бог бросал игральные кости, прежде чем решить, каким будет результат каждого физического процесса. Такая идея беспокоила Эйнштейна, и даже будучи одним из отцов квантовой физики, он впоследствии начал критиковать этот взгляд.
Может показаться, будто квантовая физика подрывает саму идею о том, что Природа управляется законами, но дело обстоит не так. Просто это ведет нас к принятию новой формы детерминизма: данное состояние системы в некоторый момент времени и законы природы определяют вероятности различных вариантов будущего и прошлого, но не определяют будущее и прошлое строго однозначно. Ученые, несмотря на то что кому-то это не по вкусу, должны придерживаться тех теорий, которые согласуются с экспериментом, а не с их собственными предвзятыми понятиями.
Возможность проверки — вот что должна требовать наука от теории. Если бы вероятностная природа предсказаний в квантовой физике означала, что подтвердить предсказания невозможно, то квантовые теории не считались бы правомерными. Но несмотря на вероятностную природу их предсказаний, мы все же можем выполнять проверку квантовых теорий. Например, мы можем повторить эксперимент много раз и подтвердить, что частота разных результатов совпадает с предсказанной вероятностью. Вернемся к опыту с бакиболами. Квантовая физика говорит нам, что никакой объект никогда не располагается в определенной точке, потому что, будь это так, неуверенность в импульсе равнялась бы бесконечности. Фактически, согласно квантовой физике, каждая частица имеет некоторую вероятность быть обнаруженной где угодно во Вселенной. Так что даже если шанс обнаружить данный электрон внутри двухщелевого устройства весьма высок, всегда будет сохраняться шанс, что этот электрон может оказаться на обратной стороне звезды альфа Центавра или внутри запеканки, приготовленной в столовой у вас на работе. В результате, если вы ударите по квантовому бакиболу, отправив его в полет, никакая ловкость и никакие знания не помогут вам заранее сказать, где точно он приземлится. Но если вы повторите этот эксперимент многократно, то полученные вами данные покажут вероятность нахождения «мяча» в разных местах и можно будет утверждать, что результаты проведенных опытов согласуются с предсказаниями теории.
Важно осознавать, что вероятности в квантовой физике не похожи на вероятности в Ньютоновой физике или в повседневной жизни. Мы можем понять это, сравнив узоры, созданные непрерывным потоком бакиболов, летящих к экрану, с узором из ямок, оставленных на мишени для игры в дартс дротиками, которыми игроки целились в «яблочко». Если игроки не перебрали пива, то шансы каждого дротика попасть в центр наибольшие, но они уменьшаются, если игрок отдаляется от мишени. Как и в случае с бакиболами, каждый дротик может попасть куда угодно, и через некоторое время на мишени появится узор из ямок, отображающий эту вероятность. В повседневной жизни про данную ситуацию мы могли бы сказать, что дротик имеет определенную вероятность попасть в разные точки; но если мы скажем так, то, в отличие от случая с бакиболами, лишь потому, что не полностью знаем условия в момент броска. Наше описание можно улучшить, если иметь точные сведения об особенностях того, как игрок бросает дротик: под каким углом, с каким вращением, скоростью и т. д. В принципе тогда мы могли бы с любой необходимой для нас точностью предсказать, куда попадет дротик. Поэтому использование нами вероятностных терминов для описания результатов событий, наблюдаемых в повседневной жизни, отражает не внутреннюю природу процесса, а только недостаток наших знаний о некоторых его аспектах.
В квантовой физике вероятности не таковы. В квантовой физике они отражают фундаментальную неупорядоченность природы. Квантовая модель природы содержит в себе принципы, противоречащие не только нашему повседневному опыту, но и нашему интуитивному пониманию реальности. Те, кто считает данные принципы фантастическими и для кого в них трудно поверить, попали в хорошую компанию, оказавшись вместе с такими великими физиками, как Эйнштейн и даже Фейнман, чье описание квантовой теории мы представим далее. Действительно, Фейнман однажды написал: «Думаю, я могу с уверенностью сказать, что квантовую механику не понимает никго». Но квантовая физика согласуется с наблюдениями. Она всегда выдерживала проверки, а проверяли ее больше, чем любую другую научную теорию.
В 1940-х годах американского физика Ричарда Фейнмана осенила потрясающая догадка относительно разницы между квантовым и Ньютоновым мирами. Фейнман заинтересовался, как появляется интерференционный узор в эксперименте с двухщелевой преградой. Напомним, что узор, который образуется, когда мы стреляем молекулами при обеих открытых щелях, не является суммой узоров, возникающей, если эксперимент провести дважды: открыв первый раз одну из щелей, а второй раз другую. Вместо этого при обеих открытых щелях мы обнаруживаем чередование светлых и темных полос. Темные полосы — это области, куда частицы вообще не попадают. Значит, частицы, которые попали бы в это место, если открыта, скажем, только левая щель, не попадают туда, если открыты обе щели. Похоже, будто в неком месте на пути от источника к экрану частицы получают информацию об обеих щелях. Такое поведение частиц резко отличается от поведения предметов в повседневной жизни, когда мяч пролетел бы через одну из щелей независимо от того, открыта вторая или нет.
Согласно Ньютоновой физике (и согласно тому, как выглядел бы эксперимент, выполненный с футбольными мячами, а не с молекулами), каждая частица следует от источника к экрану по единственному, строго определенному маршруту. Эта картина лишена «объезда», при котором частица на пути к цели могла бы посетить окрестности каждой из щелей. Согласно же квантовой модели, частица считается не имеющей определенного положения в течение времени, пока она находится между начальной и конечной точками. Фейнман понял, что не нужно интерпретировать это так, будто частицы не имеют маршрута при своем перемещении от источника до экрана. Напротив, это может означать, что частицы следуют по всем возможным траекториям, соединяющим эти точки. Вот это, заявил Фейнман, и отличает квантовую физику от Ньютоновой. Состояние обеих щелей имеет значение, потому что частицы летят не по единственной определенной траектории, а по всем возможным траекториям и делают это одновременно! Звучит как научная фантастика, но это вовсе не фантастика. Фейнман сформулировал математическое выражение (фейнмановскую сумму по историям), отражающее эту идею и воспроизводящее все законы квантовой физики. В теории Фейнмана математическая и физическая картины отличаются от первоначальной формулировки квантовой физики, но предсказания остаются теми же.
Применительно к двухщелевому эксперименту идеи Фейнмана означают, что частицы движутся по траекториям, проходящим только через левую щель или только через правую щель; что частицы, пролетевшие сквозь левую щель, возвращаются через правую, а потом снова пролетают через левую; что по пути домой они посещают ресторан, где подают замечательные креветки с карри, а потом делают несколько оборотов вокруг Юпитера; что траектории частиц могут далее пролегать туда и обратно через всю Вселенную. По мнению Фейнмана, это объясняет, как частица получает информацию о том, которая из двух щелей открыта, — если щель открыта, частица проходит через нее. Когда открыты обе щели, траектории, по которым частица движется сквозь одну щель, могут накладываться на траектории, по которым она движется сквозь другую щель, что и вызывает интерференцию. Это может показаться безумием, но для задач современной фундаментальной физики (как и для задач этой книги) формулировка Фейнмана оказалась более подходящей, чем первоначальная.
Фейнмановский взгляд на квантовую реальность крайне важен для понимания теорий, которые мы представим далее, поэтому стоит потратить немного времени, чтобы ощутить, как все это работает. Представьте себе простой процесс, в котором частица начинает свой путь в какой-то точке А и свободно движется. В Ньютоновой модели эта частица будет двигаться по прямой.

Траектории частицы. Фейнмановская формулировка квантовой теории дает картину, объясняющую, почему частицы — такие как бакиболы и электроны, — проходя через двухщелевую преграду, образуют на экране интерференционный узор.
Через некоторое точно определенное время мы обнаружим частицу именно в некоторой точке В, расположенной на этой линии. В фейнмановской модели квантовая частица «пробует» каждую траекторию, соединяющую точки А и В, собирая для каждой траектории числа, называемые фазой. Фаза отображает местоположение в цикле волны, то есть находится ли волна в положении гребня или впадины либо в каком-то промежуточном состоянии между ними. Математическое выражение, предложенное Фейнманом для расчета этой фазы, показало: если сложить вместе волны по всем траекториям, получится правильная вероятность того, что частица, начав свой путь в точке А, достигнет точки В.
Фазу, которую каждая отдельная траектория вносит в фейнмановскую сумму (а следовательно, в вероятность движения из точки А в точку В), можно изобразить в виде стрелки, имеющей фиксированную длину, а указывать стрелка может в любом направлении. Чтобы сложить две фазы, вы приставляете стрелку, соответствующую одной фазе, к концу стрелки, соответствующей другой фазе, и получаете новую стрелку, представляющую собой сумму. Чтобы прибавить дополнительные фазы, нужно просто продолжить этот процесс. Заметьте: когда фазы совпадают по направлению, суммарная стрелка может оказаться довольно длинной. Если они указывают в разные стороны, то имеют тенденцию при сложении гасить друг друга, и от стрелки может не остаться почти ничего. Эта идея проиллюстрирована ниже.
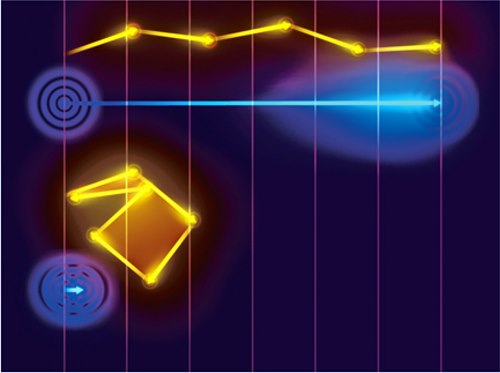
Сложение фейнмановских траекторий. Эффекты из-за различных фейнмановских траекторий могут усиливать или ослаблять друг друга точно так же, как это делают волны. Желтые стрелки — складываемые фазы. Голубые — сумма траекторий (от хвоста первой стрелки до острия последней). Ниже стрелки направлены по-разному, поэтому сумма траекторий очень короткая.
Чтобы выполнить требование Фейнмана для расчета вероятности, с которой частица, вылетевшая из точки А, прилетит в точку В, нужно сложить все фазы, или стрелки, относящиеся к каждой траектории, соединяющей точки А и В. Таких траекторий бесконечное множество, что несколько усложняет математические вычисления, тем не менее результат достижим. Некоторые из путей показаны на рисунке ниже.
Теория Фейнмана дает особенно ясное понимание того, каким образом Ньютонова картина мира проистекает из квантовой физики, которая кажется весьма отличающейся от нее. Согласно теории Фейнмана, фазы, связанные с каждой траекторией, зависят от постоянной Планка. Поскольку постоянная Планка очень мала, то, когда вы суммируете вклады от близких друг к другу траекторий, фазы обычно очень сильно различаются, и поэтому их сумма стремится к нулю (см. ил., с. 88).

Траектории от точки А до точки В. «Классическая» траектория между двумя точками — прямая линия. Фазы траекторий, близких к классической, имеют тенденцию усиливать друг друга, тогда как для фаз удаленных траекторий характерно взаимное ослабление.
Но теория также показывает, что существуют определенные траектории, для которых фазы имеют тенденцию выстраиваться в линию, и потому эти траектории предпочтительны, то есть они дают больший вклад в наблюдаемое поведение частицы. Получается, что для больших объектов траектории, очень близкие к траекториям, предсказанным теорией Ньютона, имеют схожие фазы и суммируются друг с другом, давая гораздо больший вклад в итоговую величину. Поэтому единственным назначением, имеющим вероятность гораздо больше нуля, является направление, предсказываемое теорией Ньютона, а это направление имеет вероятность, очень близкую к единице. Следовательно, большие объекты движутся именно так, как им предписывает теория Ньютона.
До сих пор мы обсуждали идеи Фейнмана в контексте эксперимента с двухщелевой преградой. В том эксперименте частицами обстреливалась преграда в виде стенки со щелями, а на расположенном за преградой экране мы могли определять, в какие места они попадают. Говоря в целом, теория Фейнмана позволяет нам предсказать вероятное поведение не только одной частицы, но и системы, которая может состоять из частицы, множества частиц или даже из целой Вселенной. За время, прошедшее от начального состояния системы до некого более позднего момента, когда мы проводим определения свойств данной системы, происходит какое-то изменение этих свойств, называемое физиками историей системы. Например, в эксперименте с двухщелевой преградой историей частицы является просто ее траектория. В таком эксперименте шанс наблюдать попадание частицы в какую-либо точку зависит от всех путей, которые могут привести туда частицу. Фейнман показал, что точно так же и для любой системы вероятность какого-либо наблюдения составляется из всех возможных историй, которые могли бы привести к данному наблюдению. Поэтому его метод называется в квантовой физике «сумма по историям» или «альтернативные истории».
Теперь, когда мы разобрались с фейнмановским подходом к квантовой физике, наступило время рассмотреть еще один ключевой квантовый принцип, который нам понадобится позже, а именно: наблюдение за системой должно изменять ее ход. Разве нельзя (как мы это делаем, увидев каплю горчицы на подбородке у начальницы) просто наблюдать, но не вмешиваться? Нельзя! Согласно квантовой физике, вы не можете «просто» наблюдать что-либо. То есть квантовая физика считает, что, наблюдая, вы должны взаимодействовать с наблюдаемым объектом. Например, чтобы рассмотреть объект в обычном смысле, мы направляем на него свет. Если свет упадет на тыкву, он, конечно же, окажет на нее слабое влияние. Но попадание даже тусклого света на крошечную квантовую частицу — то есть попадание в нее фотонов — имеет значительный эффект, и эксперименты показывают, что это влияет на результаты опыта именно так, как описывает квантовая физика.
Предположим, что, как и раньше, мы посылаем поток частиц через двухщелевую преграду и собираем данные о первом миллионе частиц, прошедших сквозь щели. Когда мы графически изобразим множество частиц, попавших в разные точки экрана, то получим интерференционный узор (см. ил., с. 73), а когда мы сложим фазы, соответствующие всем возможным путям от точки А — места старта частицы — до точки В — места ее регистрации на экране, — то обнаружим, что рассчитанная вероятность попадания в разные точки совпадает с этими данными.
Теперь предположим, что мы повторяем эксперимент, на этот раз направляя свет на щели так, чтобы мы знали промежуточный пункт — точку С, — через который прошла частица. (Точка С — это положение либо одной, либо другой щели.) Это называется «информация „который путь“», потому что она говорит нам о том, каким путем каждая частица перемещается из точки А в точку В — через щель 1 или через щель 2. Поскольку мы знаем, через какую щель прошла каждая частица, то в нашей сумме траектории для этой частицы будут теперь включать только те пути, которые проходят через щель 1, или только те, что проходят через щель 2. Сумма не будет учитывать траектории, проходящие через обе щели. Поскольку Фейнман объяснил интерференционную картину тем, что траектории, проходящие через одну щель, накладываются на траектории, проходящие через другую, то если вы включите свет, чтобы определить, через какую щель проходят частицы, тем самым лишая их другой возможности, вы получите исчезновение интерференционной картины. И действительно, когда проводился эксперимент, включение света изменяло результаты: вместо интерференционного узора, представленного на с. 73, возникала картина, приведенная на с. 72! Более того, мы можем изменять условия эксперимента, используя свет настолько слабый, что не все частицы взаимодействуют с ним. В этом случае мы можем получить информацию «который путь» только для некоторой группы частиц. Если мы затем разделим данные по частицам в соответствии с тем, получена или нет для них информация «который путь», то обнаружим, что данные, относящиеся к группе, для которой нет такой информации, создадут интерференционный узор, а данные, относящиеся к частицам другой группы — для которых есть информация «который путь», — интерференционной картины не дадут.
Это имеет важные последствия для нашего понимания «прошлого». В теории Ньютона прошлое принималось существующим как определенная последовательность событий. Если вы видите, что ваза, купленная вами в прошлом году в Италии, лежит разбитая на полу, а ваш малыш стоит над ней с растерянным видом, вы можете восстановить события, приведшие к этому случаю: маленькие пальчики не удержали вазу, она упала и, ударившись об пол, разлетелась на тысячу осколков. Действительно, имея полную информацию о настоящем, законы Ньютона позволяют воссоздать полную картину прошлого. Это согласуется с нашим интуитивным пониманием того, что у мира — плохо это или хорошо — имеется определяемое прошлое. Возможно, не было никого, кто наблюдал бы нечто в прошлом, тем не менее существование прошлого столь же несомненно, как если бы оно было запечатлено вами на серии фотоснимков. Но о квантовом бакиболе нельзя сказать, что он прошел вполне определенный путь от источника до экрана. Мы могли бы зафиксировать местоположение бакибола, наблюдая его, но в промежутке между нашими наблюдениями он проходит по всем возможным траекториям. Квантовая физика говорит нам, что, независимо от того, насколько полно наше наблюдение за настоящим, ненаблюдаемое прошлое, как и будущее, выглядит неопределенно и существует только как спектр возможностей. Согласно квантовой физике, Вселенная не имеет единственного прошлого, или единственной истории.
То, что прошлое не имеет определенности, означает, что наши наблюдения за системой, выполняемые в настоящем, влияют на ее прошлое. Это довольно эффектно демонстрирует эксперимент, который предложил американский физик Джон Уилер (1911–2008), — так называемый эксперимент с отложенным выбором. В общих чертах этот эксперимент напоминает только что рассмотренный нами эксперимент с двухщелевой преградой, в котором вы можете наблюдать траекторию движения частицы, за исключением того, что в эксперименте с отложенным выбором вы откладываете свое решение о том, проводить наблюдение за траекторией или нет, до самого последнего мгновения, предшествующего столкновению частицы с экраном.
Эксперимент с отложенным выбором приводит к данным, идентичным тем, что получаются в случае, когда мы решаем наблюдать (или не наблюдать) для получения информации «который путь», следя за самими щелями. Но при отложенном выборе траектория каждой частицы, то есть ее прошлое, определяется намного позже того, как частица пройдет сквозь щели и предположительно уже «решила», проходить ли ей только через одну щель — что не приведет к интерференции — или через обе — что создаст интерференцию.
Уилер даже рассмотрел космическую версию этого эксперимента, в которой частицами являются фотоны, испускаемые мощными квазарами, находящимися на расстоянии в миллиарды световых лет. Такой свет мог бы разделиться на две траектории и снова сфокусироваться в направлении к Земле так называемым гравитационным линзированием с помощью промежуточной галактики. Хотя подобный эксперимент находится за пределами возможностей нынешних технологий, если бы мы смогли собрать достаточно фотонов от такого света, они должны были бы сложиться в интерференционный узор. Однако если мы установим измеряющее устройство для получения информации «который путь» неподалеку от экрана, интерференционная картина не возникнет. Выбор — двигаться по одной или по двум траекториям — в этом случае был бы сделан миллиарды лет назад, еще до того как образовалась Земля, а возможно, даже и само Солнце. И все же наши наблюдения в лаборатории окажут влияние на этот выбор.
В этой главе мы проиллюстрировали использование квантовой физикой эксперимента с двухщелевой преградой. В следующей главе мы рассмотрим фейнмановскую формулировку квантовой механики на примере всей Вселенной. Мы увидим, что, подобно частице, Вселенная имеет не единственную историю, а все возможные истории, каждую со своей собственной вероятностью, а наши наблюдения ее текущего состояния влияют на ее прошлое и определяют различные истории Вселенной точно так же, как наблюдения за частицами в двухщелевом эксперименте влияют на прошлое частиц. Этот анализ покажет, как в результате Большого взрыва возникли законы природы в нашей Вселенной. Но прежде чем рассматривать, как возникают законы, мы немного поговорим о том, что же такое законы, а также о тех загадках, которые они влекут за собой.

Назад: 3. Что такое реальность
Дальше: 5. Теория всего

