Книга: Мир многих миров. Физики в поисках иных вселенных.
Назад: Глава 14 Заурядность, возведенная в принцип
Дальше: Часть IV. До начала
Глава 15
Теория Всего
Что меня по-настоящему интересует — мог ли Бог сотворить мир иным, то есть оставляют ли требования логической простоты хоть какую-то свободу.Альберт Эйнштейн
В поисках окончательной теории
Антропная картина мира держится на предположении, что фундаментальные постоянные могут варьироваться от одного места к другому. Но действительно ли такое возможно? Это вопрос о фундаментальной физической теории: будет ли из нее вытекать один уникальный набор констант или она предоставит более широкий набор возможностей?
Неизвестно, что представляет собой фундаментальная теория, и нет никакой гарантии, что она вообще существует, но поиск окончательной объединенной теории вдохновляет многие современные исследования в области физики элементарных частиц. Есть надежда, что за многочисленностью частиц и различиями четырех фундаментальных взаимодействий стоит единый математический закон, которые управляет всеми первичными явлениями. Из этого закона могут вытекать все свойства частиц, а также законы гравитации, электромагнетизма, сильного и слабого взаимодействий — подобно тому, как все теоремы геометрии следуют из пяти аксиом Евклида.
Характер объяснения свойств элементарных частиц, которое физики надеются получить из окончательной теории, хорошо иллюстрируется тем, как квантовая механика объяснила химические свойства элементов. В начале прошлого века атомы считались фундаментальными кирпичиками материи. Каждый тип атомов представляет определенный химический элемент, и химики накопили огромный объем данных о свойствах каждого из них и об их взаимодействии друг с другом. К тому времени было известно 92 различных элемента — для фундаментальных строительных блоков это было многовато. К счастью, работа русского химика Дмитрия Менделеева в конце XIX века открыла некоторые закономерности в этой горе данных. Менделеев упорядочил элементы по возрастанию их атомного веса и заметил, что похожие химические свойства появляются в таблице через равные интервалы. Никто, однако, не мог объяснить, почему элементы следуют этому периодическому шаблону.
К 1911 году стало ясно, что атомы все-таки не являются фундаментальными частицами. Эрнест Резерфорд продемонстрировал, что атом состоит из роя электронов, обращающихся вокруг маленького тяжелого ядра. Количественное объяснение строения атомов было получено в 1920-х годах, после создания квантовой механики. Оказалось, что электроны, грубо говоря, образуют вокруг ядра серию концентрических оболочек. Каждая оболочка может содержать строго определенное число электронов. С добавлением электронов оболочки постепенно заполняются. Химические свойства атома определяются в основном числом электронов на самой внешней его оболочке. Когда начинает заполняться новая оболочка, свойства элементов меняются аналогично — примерно так, как при заполнении предыдущей оболочки. Этим объясняется периодичность таблицы Менделеева.
В течение нескольких лет казалось, что фундаментальная структура материи наконец понята. Поль Дирак, один из основателей квантовой механики, заявил в статье 1929 года, что "все базовые физические законы, необходимые для построения математической теории большей части физики и всей химии, уже открыты". Но затем одна за другой стали появляться новые "элементарные" частицы.
Для начала атомные ядра оказались составными, сложенными из протонов и нейтронов, удерживаемых вместе сильным ядерным взаимодействием. Затем был открыт позитрон, а за ним мюон. Когда протоны врезаются друг в друга на ускорителях, возникают новые виды короткоживущих частиц. Это вовсе не означает, что протоны состоят из них. Если столкнуть два телевизора, то можно быть уверенным, что разлетающиеся обломки — это части, из которых прежде состояли устройства. Но в случае столкновения протонов некоторые образующиеся частицы будут тяжелее самих протонов. Избыток массы возникает из кинетической энергии их движения. Так что эти эксперименты со столкновениями не раскрывали внутреннее устройство протона, а лишь пополняли зоопарк частиц. К концу 1950-х годов их количество превзошло число известных элементов. Энрико Ферми, один из пионеров физики элементарных частиц, сказал, что если бы он мог запомнить названия всех частиц, то мог бы стать ботаником.
Прорыв, позволивший упорядочить эту хаотичную толпу частиц, совершили независимо друг от друга в начале 1960-х годов Мюррей Гелл-Манн из Калтеха и Ювал Нееман (Yuval Ne'eman), израильский офицер, который ушел в отставку для завершения своей диссертации по физике. Они заметили, что все сильно взаимодействующие частицы подчиняются двум типам симметрии. Позднее Гелл-Манн и — независимо — Георг Цвейг (George Zweig) из ЦЕРНа показали, что эти симметрии можно объяснить, если считать все частицы состоящими из более фундаментальных строительных блоков, которые Гелл-Манн назвал кварками. Это сократило количество элементарных частиц, но не радикально: кварки бывают трех "цветов" и шести "ароматов", так что имеется 18 кварков и столько же антикварков. В 1969 году за открытие симметрии сильно взаимодействующих частиц Гелл-Манн получил Нобелевскую премию.
Параллельно с этим схожая симметрия обнаружилась и для частиц, участвующих в слабом и электромагнитном взаимодействиях. Ключевую роль в формулировании этой электрослабой теории сыграли гарвардские физики Шелдон Глзшоу (Sheldon Glashow) и Стивен Вайнберг, а также пакистанский физик Абдус Салам. За эту работу они разделили Нобелевскую премию 1979 года. Классификация частиц в соответствии с симметриями играет роль, аналогичную периодической таблице в химии. Вдобавок было выявлено три типа частиц-переносчиков для трех фундаментальных взаимодействий: фотоны для электромагнитных сил, W- и Z-частицы для слабого взаимодействия и 8 глюонов для сильного. Все эти ингредиенты легли в основу Стандартной модели физики элементарных частиц.
Разработка Стандартной модели была завершена в 1970-е годы. Получившаяся теория дала точную математическую схему, которая могла использоваться для определения результатов столкновения любых известных частиц. Эта теория проверена в бесчисленных экспериментах на ускорителях, и на сегодня она подтверждается всеми имеющимися данными. Стандартная модель предсказала свойства W- и Z-частиц, а также дополнительных кварков — все они были позднее открыты. По любым меркам это феноменально успешная теория.
И все же Стандартная модель очевидно слишком громоздкая, чтобы признать ее окончательной теорией. Модель включает более 60 элементарных частиц — не слишком большой шаг вперед по сравнению с числом элементов таблицы Менделеева. В модели (чтобы не путать с таблицей) 25 настраиваемых параметров, которые должны выводиться из экспериментов, но с позиций теории их значения совершенно произвольны. Более того, одно важнейшее взаимодействие — гравитация — осталось за бортом этой модели. Успех Стандартной модели говорит о том, что мы на правильном пути, но ее недостатки указывают, что поиск должен продолжаться.
Проблема с гравитацией
Отсутствие гравитации в Стандартной модели — это не просто упущение. На первый взгляд гравитация похожа на электромагнетизм. Например, ньютоновская сила тяготения, так же как и кулоновское электрическое взаимодействие, обратно 'квадратично зависит от расстояния. Однако все попытки разработать квантовую теорию гравитации по аналогии с теорией электромагнитного и других взаимодействий в Стандартной модели сталкивались с непреодолимыми трудностями.
Сила электрического взаимодействия между двумя заряженными частицами возникает вследствие непрерывного обмена фотонами. Частицы подобны двум баскетболистам, которые бегут вдоль площадки, перебрасываясь мячом. Аналогично, гравитационное взаимодействие можно описать как обмен квантами гравитационного поля, которые называют гравитонами. И такое описание действительно работает довольно хорошо, пока взаимодействующие частицы находятся достаточно далеко. В этом случае гравитация слаба, а пространство-время почти плоское. (Помните — гравитация связана с искривлением пространства-времени.) Гравитоны можно представлять как маленькие бугорки, скачущие между частицами на этом плоском фоне. Однако на очень маленьких расстояниях ситуация совершенно иная. Как говорилось в главе 12, квантовые флуктуации на коротких расстояниях придают пространству-времени пенообразную геометрическую структуру (см. рис. 12.1). Мы не знаем, как описывать движение и взаимодействие частиц в такой хаотической среде. Картина частиц, движущихся сквозь гладкое пространство-время и стреляющих друг в друга гравитонами, очевидным образом не подходит к этому состоянию.
Эффекты квантовой гравитации становятся существенными на расстояниях меньше планковской длины — это невообразимо малая величина, в 1025 раз меньше размера атома. Для изучения таких расстояний частицы должны сталкиваться с колоссальной энергией, лежащей далеко за пределами возможностей самых мощных ускорителей. На гораздо больших расстояниях, доступных для наблюдения, квантовые флуктуации геометрии пространства-времени усредняются, и эффектами квантовой гравитации можно безболезненно пренебречь. Однако в поисках окончательных законов природы нельзя игнорировать конфликт между эйнштейновской общей теорией относительности и квантовой механикой. В окончательной теории должны найти отражение как гравитация, так и квантовые явления. Так что оставить гравитацию в стороне — это не выход.
Гармония струн
Большинство физиков ныне возлагает надежды на принципиально новый подход к квантовой гравитации — теорию струн. Она предлагает единое описание всех частиц и их взаимодействий. Это самый многообещающий из всех кандидатов на роль фундаментальной Теории Всего.
Согласно теории струн, частицы, подобные электронам или кваркам, которые кажутся точечными и потому считаются элементарными, на самом деле являются крошечными колеблющимися колечками из струн. Струны бесконечно тонки, а длина колечек сравнима с планковской. Частицы кажутся бесструктурными точками потому, что планковская длина крайне мала.
Струны в крошечных петлях очень сильно натянуты, и это натяжение заставляет их вибрировать подобно колеблющимся струнам скрипки или фортепьяно. На рисунке 15.1 показаны различные режимы вибраций прямой струны. В этих режимах, которые соответствуют разным музыкальным нотам, струна приобретает волнообразную форму с укладывающимися вдоль нее несколькими полуволнами. Чем больше число полуволн, тем выше нота. Режимы вибрации петель в теории струн весьма похожи (рис. 15.2), но теперь они соответствуют не различным нотам, а различным типам частиц. Все свойства частиц, такие как масса, электрический заряд и заряды, участвующие в слабом и сильном взаимодействиях, определяются точным вибрационным состоянием струнной петли. Вместо введения независимой новой сущности для каждого типа частиц мы имеем единственную сущность — струны, из которых состоят все частицы.
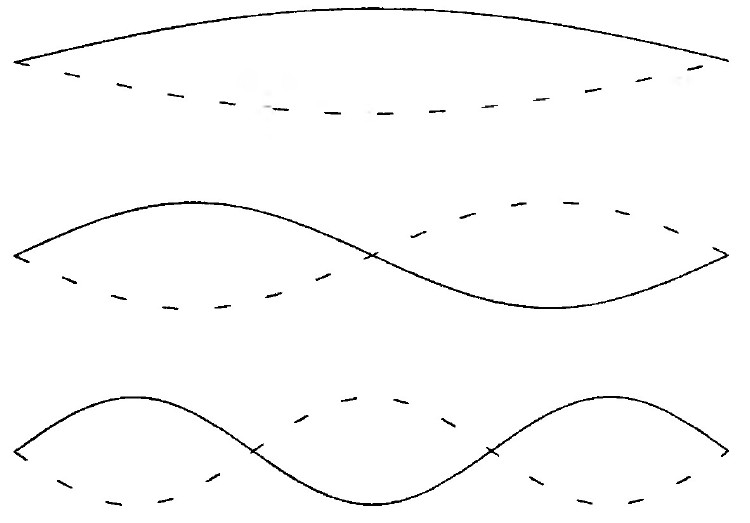
Рис. 15.1. Режимы колебаний струны.
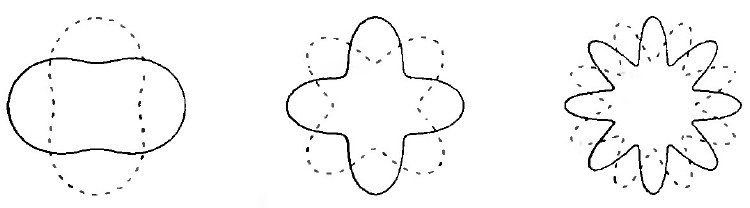
Рис. 15.2. Схематическое представление режимов вибрации струнной петли.
Частицы-переносчики — фотоны, глюоны, W и Z — также представляют собой маленькие вибрирующие колечки, а взаимодействие частиц можно изобразить как разделение и слияние струнных петель. Что особенно замечательно, спектр состояний струн с необходимостью включает гравитон — частицу, переносящую гравитационное взаимодействие. В теории струн нет проблемы объединения гравитации с другими взаимодействиями; наоборот, теорию нельзя построить без гравитации.
Конфликт между гравитацией и квантовой механикой также исчезает. Как уже говорилось, эта проблема связана с квантовыми флуктуациями геометрии пространства-времени. Если частицы — это математические точки, то флуктуации в непосредственной близости от частиц идут вразнос, а гладкий континуум пространства-времени превращается в неистовую пространственно-временную пену. В теории струн крошечные струнные колечки имеют конечные размеры, заданные планковской длиной. Это как раз тот масштаб, ниже которого квантовые флуктуации выходят из-под контроля. Петли невосприимчивы к таким субпланковским флуктуациям: пространственно-временная пена укрощается как раз в тот момент, когда она должна была начать причинять неприятности. Таким образом, впервые мы получаем согласованную квантовую теорию гравитации.
Идею о том, что частицы могут втайне быть струнами, предложили в 1970 году Еитиро Намбу (Yoichiro Nambu) из Чикагского университета, Холгер Нильсен (Holger Nielsen) из Института Нильса Бора и Леонард Сасскинд (Leonard Susskind) из Ешивы-Университета. Первоначально теория струн задумывалась как теория сильного взаимодействия, но вскоре обнаружилось, что она предсказывает существование безмассового бозона, для которого нет соответствия среди сильно взаимодействующих частиц. На ключевую идею о том, что этот безмассовый бозон имеет все свойства гравитона, указали в 1974 году Джон Шварц (John Schwarz) из Калтеха и Джоэл Шерк (Joel Sherk) из Эколь Нормаль Сюпериор. Потребовалось еще 10 лет, чтобы Шварц в сотрудничестве с Майклом Грином (Michael Green) из Колледжа королевы Марии в Лондоне справились с рядом тонких математических проблем и показали, что теория действительно является непротиворечивой.
В теории струн нет произвольных констант, так что она не допускает никаких настроек и подгонок. Все, что мы можем сделать, — это открыть ее математическую структуру и посмотреть, соответствует она реальному миру или нет. К сожалению, математика этой теории невероятно сложна. Сегодня, после 20 лет штурма сотнями талантливых физиков и математиков, она все еще остается не до конца понятной. В то же время эти исследования открыли удивительно богатые и красивые математические структуры. Это в большей мере, чем что-либо другое, указывает физикам, что они находятся на верном пути.
Ландшафт
Как я только что сказал, в теории струн нет подстроечных параметров. Это не преувеличение: их действительно нет, ни одного. Теория жестко фиксирует даже число измерений пространства. Проблема в том, что ответ в результате получается неверный: она требует, чтобы пространство имело 9 измерений вместо 3.
Это звучит довольно странно: почему мы вообще должны рассматривать теорию, которая находится в столь вопиющем противоречии с реальностью? Противоречие это можно, однако, обойти, если 6 лишних измерений свернуты или, как говорят физики, компактифицированы. Соломинка для коктейля — простейший пример компактификации: у нее есть одно большое продольное измерение и другое, свернутое в маленькую окружность. Если смотреть издали, соломинка выглядит одномерной линией, но вблизи видно, что в действительности ее поверхность — это двумерный цилиндр (рис. 15.3). Совершенно аналогично компактные дополнительные измерения могут быть невидимы, если они достаточно малы. В теории струн предполагается, что они не намного превышают планковскую длину.

Рис. 15.3. Соломинка для коктейля имеет двумерную поверхность. Большое измерение идет вдоль нее, а маленькое свернуто в окружность.
Главная проблема с дополнительными измерениями состоит в том, что неясно, каким именно образом они компактифицировались. Если бы существовало одно дополнительное измерение, оно могло бы компактифицироваться только одним способом: свернуться в окружность. Двумерная поверхность компактифицируется в сферу, в бублик или в более сложную поверхность с большим числом "ручек" (рис. 15.4). Количество вариантов растет с увеличением числа измерений. Колебательные состояния струн зависят от размеров и формы дополнительных измерений, так что каждая новая компактификация соответствует новому вакууму с иными типами частиц, имеющими другие массы и другие взаимодействия.

Рис. 15.4. Различные способы компактификации двух дополнительных измерений. Большие, некомпактифицированные измерения не показаны.
Струнные теоретики надеялись, что в итоге теория даст единственную компактификацию, которая описывает наш мир, и мы получим наконец объяснение наблюдаемых значений всех параметров элементарных частиц. На волне энтузиазма, которая последовала за математическими прорывами 1980-х годов, казалось, что эта цель вот-вот будет достигнута, и теорию струн называли будущей "Теорией Всего" — высокое звание для концепции, которой еще только предстоит сделать свои первые наблюдаемые предсказания! Но постепенно стала вырисовываться совершенно иная картина: теория, как выяснилось, допускает тысячи различных компактификаций.
Это было бы полбеды, но в середине 1990-х годов ситуация еще ухудшилась из-за некоторых неожиданных открытий. По мере того как улучшалось понимание математики теории струн, становилось ясно, что вдобавок к одномерным струнам теория должна включать двумерные мембраны, а также их многомерные аналоги. Все эти новые объекты собирательно называются бранами. Маленькие вибрирующие браны должны выглядеть как частицы, но они слишком массивны, чтобы рождаться на ускорителях.
С бранами связан один неприятный эффект: они радикально увеличивают число способов, которыми можно конструировать новые виды вакуума. Брана может как резиновая лента накручиваться на некоторые компактные измерения. Каждая стабильная конфигурация браны дает новый тип вакуума. Можно накрутить одну, две и более бран на каждую ручку компактного пространства, и при большом числе ручек количество вариантов становится просто чудовищным. В уравнениях теории нет подстроечных констант, но их решения, описывающие различные состояния вакуума, характеризуются сотнями параметров: размерами компактных измерений, расположением бран и т.п.
Если у нас есть один параметр, это очень похоже на скалярное поле в обычной физике элементарных частиц. Как говорилось в предыдущих главах, оно ведет себя подобно маленькому шарику на энергетическом ландшафте и катится к ближайшему минимуму плотности энергии. С двумя параметрами ландшафт становится двумерным, как показано на рисунке 15.5. У него есть максимумы (пики) и минимумы (долины), причем последние соответствуют состояниям вакуума. Высота каждого минимума задает соответствующую плотность энергии вакуума (космологическую постоянную).

Рис. 15.5. Двумерный энергетический ландшафт. Каждое измерение (не путать с измерениями обычного пространства) представляет один параметр, характеризующий вакуум теории струн.
Действительный энергетический ландшафт теории струн гораздо сложнее, поскольку он включает куда больше параметров. Этот ландшафт нельзя изобразить на листе бумаги: чтобы учесть все параметры, нужно пространство с несколькими сотнями измерений. Но ландшафт можно анализировать математическими методами. Грубые оценки показывают, что он содержит около 10500 (гугол в пятой степени!) различных вакуумов. Некоторые из них похожи на наш; другие имеют совершенно иные значения фундаментальных постоянных. Третьи отличаются еще радикальнее: они поддерживают совершенно иные частицы и взаимодействия или имеют свыше трех больших измерений.
Когда стали проступать контуры этого ландшафта, надежда вывести из теории струн один уникальный тип вакуума быстро развеялась. Однако струнные теоретики это отрицали и были не готовы признать поражение.
Пузырящаяся Вселенная
Первыми физиками, которые откололись от стаи, были Рафаэль Буссо (Raphael Bousso), ныне работающий в Калифорнийском университете в Беркли, и Джозеф Полчински из Института теоретической физики Кавли в Санта-Барбаре. Помните Полчински? Это тот самый струнный теоретик, который на дух не переносил антропный принцип и обещал бросить физику, если будет открыта космологическая постоянная. К счастью, он изменил свое мнение как по части ухода из физики, так и в отношении антропного принципа.
Буссо и Полчински объединили картину струнного ландшафта с идеями инфляционной космологии и показали, что в ходе вечной инфляции будут порождаться области со всеми возможными вакуумами. Самый высокоэнергичный вакуум будет расширяться быстрее всех. На этом инфляционном фоне будут зарождаться пузырьки менее энергичных вакуумов (как в первоначальном инфляционном сценарии Гута, описанном в главах 5 и 6). Внутренние области пузырьков будут инфлировать в меньшем темпе, и в них будут появляться пузырьки с еще меньшей энергией (рис. 15.6). В результате будет задействован весь ландшафт теории струн — образуется бесчисленное количество пузырьков со всеми возможными типами вакуума.

Рис. 15.6. Пузырьки, заполненные низкоэнергетическим вакуумом, зарождаются на расширяющемся высокоэнергетическом фоне, и еще менее энергетические пузырьки появляются внутри них.
Мы живем в одном из пузырьков, но теория не говорит, в каком именно. Лишь очень малая доля из них пригодна для жизни, и мы должны оказаться именно в одном из таких редких пузырьков. То, что именно такая картина используется в антропных рассуждениях, стало большой неожиданностью для многих струнных теоретиков. Если теория струн действительно окончательная Теория Всего, то, по-видимому, антропное мировоззрение неизбежно.
Надо сказать, что еще далеко не весь ландшафт теории струн картирован. Чтобы получалась реалистичная космология, некоторые склоны должны быть очень пологими, допускающими медленно катящуюся инфляцию. Недавние работы показывают, что такие участки ландшафта действительно существуют. Но надо найти еще более пологие склоны, требуемые для скалярного поля Линде в модели переменной космологической "постоянной" (обсуждавшейся в главе 13). Пока таких не обнаружено. Но Буссо и Полчински полагают, что среди гуголов вакуумов струнного ландшафта найдутся подходящие варианты.
Вместо континуума плотностей энергий вакуума в модели Линде ландшафт теории струн предлагает дискретный набор значений. Это могло бы стать проблемой, поскольку лишь крошечная доля этих значений (примерно 1 из 10120) попадает в небольшой антропно приемлемый диапазон. Если бы у нас было меньше 10120 вакуумов, этот диапазон вполне мог бы оказаться пустым. Но при 10500 разных вакуумов в ландшафте набор значений оказывается столь плотным, что становится почти непрерывным, и можно ожидать, что гуголы вакуумов будут иметь космологическую постоянную в антропно приемлемом интервале. Тем самым, принцип заурядности по-прежнему остается в силе, и в успешном предсказании наблюдаемого значения космологической постоянной ничего не меняется.
Программа на XXI век
Статья Буссо и Полчински, появившаяся в 2000 году, вызвала подвижку, но настоящий обвал начался три года спустя, когда к ним присоединился изобретатель теории струн Леонард Сасскинд из Стэнфорда. Это на удивление независимый мыслитель, а также чрезвычайно привлекательный и харизматичный человек. У него феноменальная способность убеждать; словом, это тот человек, которого хочется иметь на своей стороне.
Сасскинд по-прежнему не соглашался с первой статьей Буссо и Полчински. Он чувствовал, что содержащееся в статье предположение о существовании множества вакуумов является скорее догадкой, чем математическим фактом. Но работы следующих нескольких лет показали, что догадки были весьма глубокими, и в 2003 году Сасскинд стал в полную силу поддерживать то, что он назвал "антропным ландшафтом теории струн". Он доказывал, что разнообразие вакуумов в теории струн впервые дает серьезную научную основу для антропной аргументации. Струнные теоретики, говорил он, должны поэтому поддерживать антропный принцип, а не бороться с ним.
Менее чем через год все вокруг уже говорили о "ландшафте". Число статей, в которых обсуждалась множественность вакуумов и другие антропные вопросы, выросло с четырех в 2002 году до тридцати двух в 2004-м. Конечно, не всем понравился такой поворот дел. "Я ненавижу новую идею ландшафта, — говорил Пол Стейнхардт, — и надеюсь, что она сгинет". Дэвид Гросс, лауреат Нобелевской премии 2004 года, считающий антропный принцип отступлением от идеала единственности, перефразировал Уинстона Черчилля, говоря: "Никогда, никогда, никогда, никогда не отступайте!" Когда я беседовал с ним на конференции в Кливленде, он жаловался, что антропный принцип подобен вирусу. Однажды заразившись, вы потеряны для сообщества. "Эд Виттен терпеть не может эту идею, — говорит Сасскинд, описывая ситуацию, — но, по-моему, его очень беспокоит то, что она может оказаться верной. Ему это не нравится, но, я думаю, он понимает, что все к тому идет".
Если ландшафтные идеи верны, объяснить наблюдаемые значения фундаментальных постоянных будет непросто. Во-первых, нам нужна карта ландшафта. Какие типы вакуумов на ней есть и сколько объектов внутри каждого типа? Конечно, нельзя надеяться детально охарактеризовать все 10500 вакуумов, так что понадобится некое статистическое описание. Необходимо также оценить вероятности появления пузырьков с одним типом вакуума по сравнению с другим. После этого у нас будут все ингредиенты для разработки модели вечно инфлирующей Вселенной с пузырьками внутри пузырьков внутри пузырьков, как показано на рисунке 15.6. Построив эту модель, можно применить принцип заурядности для определения вероятности нашего существования в том или ином типе вакуума.
Сейчас мы делаем лишь первые пробные шаги в этой исследовательской программе, и впереди лежат труднопреодолимые препятствия. "Однако, — пишет Леонард Сасскинд, — я готов держать пари, что к началу XXII века философы и физики будут с ностальгией оглядываться на наше настоящее, вспоминая золотой век, когда узкая и ограниченная концепция Вселенной XX века уступила место гораздо более широкому и масштабному мегаверсу, населяющему ландшафт ошеломительных размеров".
Назад: Глава 14 Заурядность, возведенная в принцип
Дальше: Часть IV. До начала

