Книга: Мир многих миров. Физики в поисках иных вселенных.
Назад: Глава 13 Антропные владения
Дальше: Глава 15 Теория Всего
Глава 14
Заурядность, возведенная в принцип
Я считаю себя средним человеком, за исключением того факта, что я считаю себя средним человеком.Мишель Монтень (1533-1592)
Колоколообразная кривая
Самая серьезная критика антропного принципа связана с тем, что он не дает никаких проверяемых предсказаний. Весь его смысл сводится к тому, что мы можем наблюдать лишь такие значения постоянных, которые позволяют существовать наблюдателям. Это утверждение трудно считать предсказанием, поскольку оно с гарантией истинно. Вопрос в том, можем ли мы предложить что-то получше? Можно ли извлечь из антропных рассуждений какие-то нетривиальные предсказания?
Если величины, которые я собираюсь измерить, могут случайным образом принимать значения в широком диапазоне, то мне не удастся уверенно предсказать результаты измерений. Но я могу по крайней мере сделать статистическое предсказание. Допустим, я хочу предсказать рост первого встречного человека на улице. Согласно "Книге рекордов Гиннесса", самым высоким человеком в истории медицины был американец Роберт Першинг Уэдлоу, чей рост составлял 2,72 метра. Самый низкий взрослый человек, индиец Гал Мохаммед, имел рост 57 сантиметров. Чтобы быть уверенным в успехе, мне следует предсказать, что первый встречный будет иметь рост где-то между этими крайними значениями. Если только рекорды Гиннесса не будут побиты, это предсказание с гарантией окажется правильным.
Чтобы сделать более содержательное предсказание, мне следует изучить статистические данные о росте жителей Соединенных Штатов. Распределение по росту описывается колоколообразной кривой, изображенной на рисунке 14.1, с медианой 1,77 метра (50% людей ниже и 50% — выше этого значения). Вряд ли первый встречный окажется великаном или карликом, поэтому я могу ожидать, что его рост окажется где-то около середины распределения. Чтобы сделать предсказание более определенным, я могу допустить, что он не будет из числа 2,5% самых низкорослых или из 2,5% самых высоких американцев. Остальные 95% имеют рост от 1,63 до 1,90 метра. Если я предскажу, что встречный будет иметь рост в этом диапазоне, а затем многократно проведу эксперимент, можно ожидать, что в 95% случаев я буду прав. Это называется предсказанием с точностью 95%.
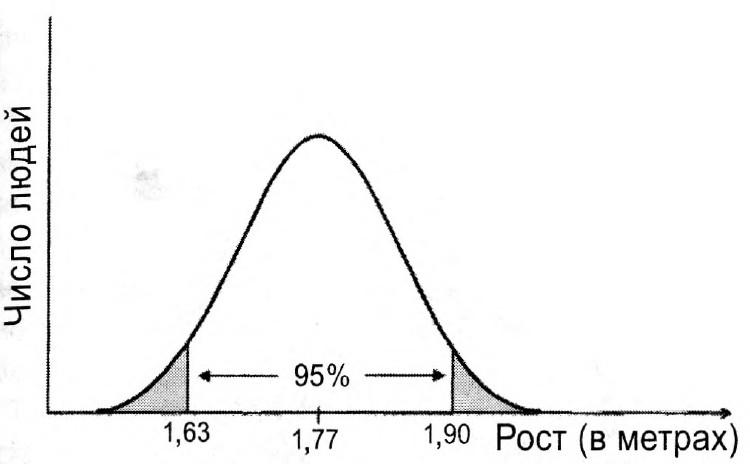
Рис. 14.1. Распределение американцев по росту. Число людей с ростом в определенном интервале пропорционально площади под соответствующим участком кривой. Серые "хвосты" колоколообразной кривой соответствуют 2,5% на нижнем и верхнем участках распределения. Попадание в диапазон между этими отмеченными областями предсказывается с точностью в 95%.
Чтобы сделать предсказание с точностью 99%, мне следует отбросить по 0,5% с обоих концов распределения. Чем выше точность, тем меньше мои шансы ошибиться, но прогнозируемый диапазон роста становится все шире, а само предсказание — все менее интересным.
Можно ли применить аналогичную технику к предсказанию фундаментальных постоянных? Я пытался найти ответ на этот вопрос летом 1994 года, когда гостил у моего друга Тибо Дамура (Thibault Damour) во французском Институте высших научных исследований. Институт расположен в небольшой деревушке Бюр-сюр-Иветт (Bures sur Yvette) в 30 минутах поездом от Парижа. Мне нравится французская провинция, французское вино и — несмотря на всю ее калорийность — французская кухня. Знаменитый российский физик Лев Ландау часто говорил, что один бокал спиртного убивает его вдохновение на неделю. К счастью, это не мой случай. Вечером, воодушевленный замечательным ужином, я прогуливался по лугам вдоль берегов речки Иветт, а мои мысли постепенно вернулись к проблеме антропных предсказаний.
Допустим, что фундаментальная постоянная, назовем ее X, меняется от одной области Вселенной к другой. В некоторых областях присутствие наблюдателей невозможно, а в других они могут существовать, и значение X будет измерено. Предположим также, что некое Статистическое бюро Вселенной собирает и публикует результаты этих измерений. Распределение значений, измеренных различными наблюдателями, будет, скорее всего, иметь колоколообразную форму — подобную той, что на рисунке 14.1. Тогда мы можем отбросить 2,5% с обоих концов распределения и предсказать значение X с точностью 95%.
Рис. 14.2. Наблюдатель, случайным образом вброшенный во Вселенную. Измеренные им значения постоянных могут быть предсказаны по статистическому распределению.
Каков может быть смысл подобного предсказания? Если мы случайно вбросим наблюдателя во Вселенную, обнаруженное им значение X будет находиться в предсказанном интервале в 95% случаев. К сожалению, мы не можем проверить такого рода предсказание, поскольку все области с различными значениями X находятся далеко за горизонтом. Мы можем измерить X только в нашей местной области. Но что мы все-таки можем, так это считать свое положение случайным. Мы — лишь одна из множества цивилизаций, разбросанных по Вселенной. Априори у нас нет оснований считать, что значение X в нашей области очень редкое, иными словами, особое по сравнению с величинами, измеренными другими наблюдателями. Отсюда мы можем с точностью 95% предсказать, что наши измерения дадут значение в указанном диапазоне. Для данного подхода ключевую роль играет предположение о нашей неисключительности; я называю его "принципом заурядности".
Некоторые мои коллеги возражают против такого наименования. Вместо этого они предлагают говорить о "принципе демократии". Конечно, никто не хочет быть заурядным, но зато это слово выражает ностальгию по тем временам, когда люди находились в центре мира. Так заманчиво думать, что мы особенные, но в космологии предположение о нашей заурядности вновь и вновь оказывается очень плодотворной гипотезой.
Такого же рода рассуждения применимы и к предсказанию роста людей. Представьте на мгновение, что вы не знаете собственного роста. Тогда, чтобы предсказать его, вы можете использовать статистические данные для своей страны и пола. Если, например, вы взрослый мужчина, живущий в США, и у вас нет оснований считать себя необычно высоким или низким, то с 95-процентной уверенностью вы можете считать, что ваш рост лежит в интервале от 1,63 до 1,90 метра.
Позднее я узнал: сходные идеи уже высказывали философ Джон Лесли (John Leslie) и — независимо от него — принстонский астрофизик Ричард Готт (Richard Gott). Главным образом их интересовало предсказание долговечности человеческой расы. Они доказывали, что человечество вряд ли проживет намного дольше, чем уже существует, поскольку в противном случае мы находились бы на удивление близко к началу нашей истории. Это так называемый "аргумент судного дня". Он восходит к Брэндону Картеру, изобретателю антропного принципа, который изложил данный аргумент на своей лекции в 1983 году, но никогда не публиковал его в печати (похоже, Картеру и без того хватало спорных идей). Готт также использовал аналогичное рассуждение для предсказания падения Берлинской стены и срока жизни британского журнала Nature, где он опубликовал свою первую статью на эту тему. Последнее предсказание о том, что Nature будет выходить до 6800 года, пока остается непроверенным.
Если у нас есть статистическое распределение для фундаментальных постоянных, измеренных другими наблюдателями, мы можем, опираясь на принцип заурядности, сделать предсказание с заданным уровнем надежности. Но откуда мы получим это распределение? Вместо данных Статистического бюро Вселенной мы можем использовать результаты теоретических расчетов. Статистическое распределение нельзя узнать без теории, описывающей мультиверс с переменными константами. В настоящее время лучший кандидат на роль такой теории — это теория вечной инфляции. Как говорилось в предыдущей главе, квантовые процессы в инфлирующем пространстве-времени порождают множество доменов со всеми возможными значениями постоянных. Мы можем попробовать рассчитать распределение для констант, исходя из теории вечной инфляции, а затем — кто знает! — можем сопоставить результаты с экспериментальными данными. Тем самым, открывается захватывающая перспектива несмотря ни на что сделать вечную инфляцию объектом наблюдательной проверки. Конечно, я не мог упустить такую возможность.
Подсчет наблюдателей
Рассмотрим большой объем пространства — настолько большой, что он охватывает области со всеми возможными значениями констант. Некоторые из этих областей плотно заселены разумными наблюдателями. Другие, менее благоприятные для жизни, больше в объеме, но при этом малонаселенные. Большая часть объема будет занята громадными пустынными доменами, где наблюдателей быть не может.
Число наблюдателей, которые обнаружат определенные значения констант, определяется двумя коэффициентами: объемом тех областей, где константы имеют указанные значения (в кубических световых годах, например), и числом наблюдателей на один кубический световой год. Долю объема можно определить на основе теории инфляции в совокупности с моделью физики элементарных частиц для переменных констант (такой как модель скалярного поля для космологической постоянной). Но второй коэффициент, плотность наблюдателей, вызывает гораздо больше трудностей. Мы очень мало знаем о происхождении жизни, не говоря уже о разуме. Как тогда мы можем надеяться определить число наблюдателей?
Спасительным может стать тот факт, что некоторые константы не влияют непосредственно на физику и химию жизни. В качестве примеров можно привести космологическую постоянную, массу нейтрино и параметр, обычно обозначаемый Q, который характеризует величину первичных возмущений плотности. Изменения таких нейтральных в отношении жизни констант могут повлиять на образование галактик, но не на шансы развития жизни в конкретной галактике. Напротив, такие константы, как масса электрона или ньютоновская гравитационная постоянная, непосредственно влияют на жизненные процессы. Наше неведение относительно жизни и разума можно исключить, если мы сконцентрируемся на тех областях, где влияющие на жизнь константы имеют такие же значения, как и в наших окрестностях, а различаются только значения бионейтральных. Все галактики в таких областях будут содержать примерно одинаковое число наблюдателей, так что их плотность будет просто пропорциональна плотности галактик.
Итак, стратегия состоит в ограничении анализа бионейтральными константами. Проблема тогда сводится к вычислению количества галактик на единицу объема пространства — хорошо исследованной астрофизической задаче. Результат этих расчетов совместно с коэффициентом объема, выведенным из теории инфляции, как раз и даст нам нужное статистическое распределение.
Наступление на космологическую постоянную
Пока я размышлял о наблюдателях в далеких доменах с другими фундаментальными постоянными, было трудно поверить, что уравнения, которые я писал в своем блокноте, имеют отношение к чему-то реальному. Но, оставив этот вопрос в стороне, я смело двинулся вперед: я хотел понять, может ли принцип заурядности пролить хоть какой-то свет на проблему космологической постоянной.
Первый шаг был уже сделан Стивеном Вайнбергом. Он изучил, как влияет космологическая постоянная на образование галактик, и установил антропные границы для этой константы: значение, выше которого энергия вакуума станет доминировать во Вселенной слишком быстро, не позволяя образоваться галактикам. Более того, как я уже отмечал, Вайнберг вывел из своего анализа предсказание. Если между нулем и антропной границей мы выберем произвольное значение, оно вряд ли будет много меньше этой границы — по той же причине, по которой первый встретившийся нам человек вряд ли окажется карликом. Таким образом, Вайнберг утверждал, что значение космологической постоянной в нашей части Вселенной должно быть сравнимо с антропной границей.
Хотя эти рассуждения звучат убедительно, я должен сделать некоторые оговорки. В областях, где космологическая постоянная сравнима с антропной границей, образование галактик вряд ли возможно и плотность наблюдателей очень низка. Большинство наблюдателей окажутся в областях, изобилующих галактиками, где космологическая постоянная заметно ниже границы и достаточно мала, чтобы начать доминировать во Вселенной только после того, как процесс формирования галактик будет более или менее завершен. Принцип заурядности говорит, что мы, скорее всего, обнаружим, что оказались именно среди этих наблюдателей.
Я грубо прикинул, что космологическая постоянная, измеренная типичным наблюдателем, не должна заметно — более чем в 10 раз — превышать среднюю плотность вещества. Намного меньшие значения тоже маловероятны — так же как встреча с карликом. Этот анализ я опубликовал в 1995 году, предсказав, что в нашем регионе мы должны получить значение примерно в десять раз больше плотности вещества. Более тщательные расчеты, также основанные на принципе заурядности, были выполнены позднее оксфордским астрофизиком Джорджем Эфстатиу (George Efstathiou) и Стивеном Вайнбергом, к которым теперь присоединились Хьюго Мартел (Hugo Martel) и Пол Шапиро (Paul Shapiro). Они пришли к аналогичным выводам.
Я был крайне воодушевлен возможностью превратить антропные рассуждения в проверяемые предсказания. Но лишь очень немногие разделяли мой энтузиазм. Ведущий специалист по теории струн Джозеф Полчински Goseph Polchinski) однажды сказал, что бросит физику, если будет открыто ненулевое значение космологической постоянной. Полчински понимал, что единственное объяснение малой космологической постоянной — антропное, и он просто не мог смириться с этой мыслью. Ответом на мои доклады об антропных предсказаниях часто служила напряженная тишина. После одного из выступлений некий выдающийся принстонский космолог поднялся и сказал: "Если кто-то хочет работать над антропным принципом — пусть работает". Тон этого замечания не оставлял сомнений в том, что такие люди зря теряют время.
Спасительные сверхновые
Как я уже упоминал в предыдущих главах, первая публикация данных о ненулевом значении космологической постоянной стала настоящим шоком для большинства физиков. Результаты основывались на изучении взрывов далеких сверхновых особого вида — так называемых сверхновых типа Ia.
Считается, что эти гигантские взрывы происходят в двойных звездных системах, состоящих из активной звезды и белого карлика — компактного остатка звезды, исчерпавшей свое ядерное топливо. Одиночному белому карлику положено медленно затухать, но при наличии компаньона его жизнь может закончиться грандиозным фейерверком. Он должен захватывать часть газа, выбрасываемого звездой-компаньоном, так что его масса будет неуклонно расти. Между тем существует максимальная масса, которую может иметь белый карлик — так называемый предел Чандрасекара, — за которым гравитация вызывает коллапс, приводящий к колоссальному термоядерному взрыву. Именно его мы и наблюдаем как сверхновую типа Ia.
На небе появляется яркая точка — на пике своего блеска сверхновая может светить как 4 миллиарда звезд. В галактике вроде нашей сверхновые типа Ia вспыхивают примерно один раз в 300 лет. Чтобы засечь десятки таких взрывов, астрономы несколько лет следили за тысячами галактик. Но их усилия были вознаграждены. Сверхновые типа Ia очень близки к давней мечте астрономов о стандартной свече — классе космических объектов, которые имеют в точности одинаковую мощность излучения. Расстояния до стандартных свеч можно определить по их видимому блеску — точно так же, как расстояние до 100-ваттной лампочки определяется по создаваемой ею освещенности. Без таких волшебных объектов определение расстояний в астрономии становится удручающе сложной задачей.
Сверхновые типа Ia имеют почти одинаковую мощность, поскольку взрывающиеся белые карлики обладают одинаковой массой, равной пределу Чандрасекара. Зная эту мощность, можно определить расстояние до сверхновой, а раз нам известно расстояние, то легко найти и время взрыва — просто подсчитав, за какой срок свет покроет эту дистанцию. Кроме того, для определения скорости, с которой в то время расширялась Вселенная, можно использовать покраснение, или доплеровское смещение света. Таким образом, анализируя свет далеких сверхновых, можно выяснить историю космологического расширения.
Этот метод был усовершенствован двумя конкурирующими группами астрономов, одна из которых называлась Supernova Cosmology Project, а другая High-Z Supernova Search Team. Эти две группы соревновались в определении темпов замедления космологического расширения под действием гравитации. Но обнаружили они нечто совершенно иное. В 1998 году команда High-Z сообщила, что вместо замедления уверенно наблюдает ускорение расширения Вселенной на протяжении последних примерно пяти миллиардов лет. Чтобы сделать такое заявление, требовалась определенная смелость, поскольку ускоренное расширение было недвусмысленным признаком космологической постоянной. Когда одного из руководителей группы, Брайана Шмидта (Brian Schmidt), попросили выразить свое отношение к этому результату, он ответил: "Нечто среднее между удивлением и ужасом".
Несколько месяцев спустя команда Supernova Cosmology Project сообщила об очень похожих результатах. Как выразился руководитель этой группы Сол Перлмуттер (Saul Perl-mutter), результаты двух команд находились "в отчаянном согласии".
Открытие породило в физическом сообществе настоящую взрывную волну. Некоторые просто отказывались верить полученным результатам. Слава Муханов предложил мне поспорить на бутылку бордо, что свидетельства космологической постоянной вскоре бесследно исчезнут. Когда в итоге Муханов выставил бутылку, мы вместе насладились вином, и, похоже, присутствие космологической постоянной не повлияло на его букет.
Было также предположение, что на яркость сверхновых могут влиять факторы, отличные от расстояния. Например, если бы свет рассеивался частицами пыли в межгалактическом пространстве, сверхновые выглядели бы более тусклыми, вводя нас в заблуждение и заставляя думать, что они находятся дальше, чем есть. Эти сомнения были рассеяны спустя несколько лет Адамом Райессом (Adam Riess) из Института космического телескопа в Балтиморе, который изучал самую далекую сверхновую, известную на тот момент, — SN 1997ff. Если бы ослабление было вызвано экранирующей пылью, эффект лишь возрастал бы с расстоянием. Но эта сверхновая была ярче, а не слабее, чем должна быть в "пограничной" Вселенной, которая не ускоряется и не тормозится. Объяснение состояло в том, что она взорвалась через 3 миллиарда лет ПБВ, в эпоху, когда энергия вакуума еще не доминировала, и ускоренное расширение не началось.
По мере того как свидетельства в пользу ускоренного расширения становились все сильнее, космологи начинали понимать, что с определенной точки зрения возвращение космологической постоянной — не такая уж плохая вещь. Во-первых, как говорилось в главе 9, она обеспечивает недостающую массу, делая общую плотность Вселенной равной критической. А во-вторых, она разрешает давнюю проблему несоответствия космических возрастов. Возраст Вселенной, вычисленный без космологической постоянной, оказывался меньше возраста самых старых звезд. Если же космологическое расширение ускоряется, значит, в прошлом оно шло медленнее, и Вселенной потребовалось больше времени, чтобы расшириться до своего нынешнего размера. Космологическая постоянная делает Вселенную старше, устраняя несоответствие возрастов.
Итак, спустя всего несколько лет после открытия космологического расширения было уже трудно представить себе, как мы вообще могли без него жить. И сегодня дебаты сместились к вопросу о том, что же оно собой представляет.
Объясняя совпадение
Наблюдавшееся значение плотности энергии вакуума — примерно втрое превосходящее среднюю плотность вещества — в первом приближении соответствовало значениям, которые тремя годами раньше были предсказаны на основе принципа заурядности. Обычно физики считают успешные предсказания сильным доводом в пользу теории. Но в этот раз они не спешили признавать антропную аргументацию. В первые годы после открытия многие физики прикладывали неимоверные усилия в попытках объяснить ускоренное расширение без обращения к антропным аргументам. Самой популярной среди этих попыток была модель квинтэссенции, разработанная Полом Стейнхардтом (Paul Steinhardt) с коллегами.
Идея квинтэссенции состоит в том, что энергия вакуума не постоянна, а постепенно убывает с расширением Вселенной. Ныне она так мала потому, что Вселенная весьма стара. Точнее говоря, квинтэссенция — это скалярное поле, энергетический ландшафт которого будто специально спроектирован для скоростного лыжного спуска (рис. 14.3). Предполагается, что в ранней Вселенной поле было высоко на холме, но к настоящему времени скатилось вниз, что соответствует низкой плотности энергии вакуума.
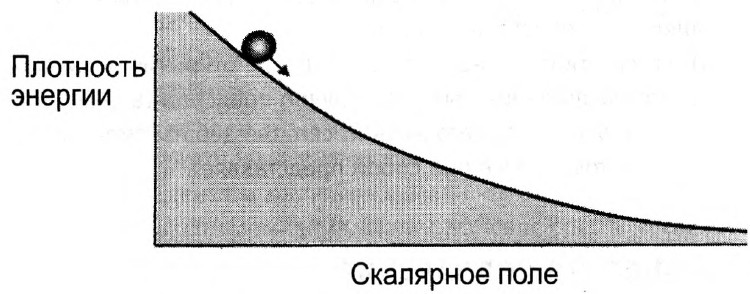
Рис. 14.3. Энергетический ландшафт квинтэссенции.
Недостаток этой модели состоит в том, что она не решает загадку совпадения — почему современная плотность энергии вакуума оказалась сравнимой с плотностью вещества (см. главу 12). Форму энергетического холма можно подобрать так, чтобы это произошло, но это будет простой подгонкой, а не объяснением данных.
С другой стороны, антропный подход предлагает естественное решение. Согласно принципу заурядности, большинство наблюдателей живет в таких областях, где плотность материи сравнялась с космологической постоянной как раз вблизи эпохи образования галактик. Формирование гигантских спиральных галактик, подобных нашей, завершилось в относительно недавнем космологическом прошлом — примерно через несколько миллиардов лет ПБВ. С тех пор плотность вещества стала ниже, чем у вакуума, но не намного (в нашей области — примерно в три раза).
Несмотря на многочисленные попытки, никакого другого способа правдоподобно объяснить это совпадение предложено не было. Постепенно коллективное сознание физиков стало привыкать к мысли, что антропная картина мира может закрепиться надолго.
За и против
Нетрудно понять, почему многие физики не хотят мириться с антропным объяснением. Стандарты точности в физике очень высоки, можно сказать, неограниченны. Впечатляющий пример дает вычисление магнитного момента электрона. Электрон можно рассматривать как крошечный магнит. Его сила характеризуется магнитным моментом, который впервые вычислил Поль Дирак в 1930-х годах. Результат очень точно согласовывался с экспериментом, но физики вскоре поняли, что имеется небольшая поправка к дираковскому значению, вызванная квантовыми флуктуациями вакуума. В результате началась гонка между теоретиками, которые выполняли все более точные расчеты, и экспериментаторами, измерявшими магнитный момент с все более и более высокой точностью. Самый последний результат измерений дает для поправочного множителя значение 1,001159652188 с погрешностью в последней цифре. Теоретическое значение еще точнее. Удивительно, что согласие между этими двумя величинами наблюдается до 11-го знака после запятой. На самом деле, если бы такого согласия не было, пусть даже расхождение наблюдалось бы только в 11-м знаке, это стало бы сигналом тревоги, указывающим на пробел в нашем понимании электрона.
Антропные предсказания не таковы. Самое большее, на что мы можем надеяться, — это вычислить колоколообразную статистическую кривую. Но даже если рассчитать ее очень точно, мы сможем предсказать только диапазон, в который значение попадет с заданной вероятностью. Дальнейшее совершенствование вычислений не приведет к впечатляющему повышению точности предсказаний. Если наблюдаемая величина попадет в предсказанный интервал, все равно еще надолго останутся сомнения, не произошло ли это в результате чисто случайного совпадения. В случае же промаха можно допустить, что теория все же верна, просто нам довелось оказаться в числе немногих наблюдателей в хвостах колоколообразной кривой.
Неудивительно, что, стоя перед таким выбором, физики не спешат отказываться от своей старой парадигмы в пользу антропной селекции. Но природа уже сделала свой выбор. Мы только выяснили, каким же он был. Если фундаментальные постоянные меняются от одной части Вселенной к другой, то, нравится нам это или нет, лучшее, что можно сделать, — это дать статистическое предсказание на основе принципа заурядности.
Наблюдаемое значение космологической постоянной — сильный довод в пользу существования действительно колоссального мультиверса. Оно попадает в диапазон значений, предсказанный из антропных соображений, а правдоподобных альтернатив, по-видимому, нет. Конечно, это свидетельство в пользу мультиверса — непрямое и всегда останется таковым. Это дело построено на косвенных уликах, и в нем не предполагается заслушивать свидетелей-очевидцев или изучать орудие преступления. Но если при некотором везении мы сделаем еще несколько удачных предсказаний, то сможем считать дело раскрытым за отсутствием обоснованных сомнений.
Назад: Глава 13 Антропные владения
Дальше: Глава 15 Теория Всего

