Стандартное отклонение

Книга: Разумное распределение активов. Как построить портфель с максимальной доходностью и минимальным риском

Теперь мы готовы рассчитать риск актива «А». Для этого рассчитывается стандартное отклонение, служащее мерой разброса множества чисел. Расчеты можно произвести вручную, однако это чересчур утомительно. Обычно они производятся с помощью электронных таблиц или финансового калькулятора. В приведенном выше примере расчета доходности за восьмилетний период стандартное отклонение доходности составило 11,46 %.

Что делать со стандартным отклонением? Прежде всего, следует ознакомиться с ним как с мерой риска. Обычно стандартное отклонение доходности для различных классов активов таково:

• денежный рынок (наличность): 2–3 %;

• краткосрочные облигации: 3–5 %;

• долгосрочные облигации: 6–8 %;

• акции компаний США (консервативные активы): 10–14 %;

• акции компаний США (агрессивные активы): 15–25 %;

• акции иностранных компаний: 15–25 %;

• акции компаний развивающихся стран: 25–35 %.

Рейтинговые службы практически всех взаимных фондов приводят в своих отчетах величины стандартного отклонения. Morningstar (www.morningstar.com), компания, занимающаяся сбором информации и анализом деятельности взаимных фондов, указывает стандартные отклонения годовой доходности за предыдущие 3, 5 и 10 лет. В некоторых случаях вы можете иметь доход только за один или два года. Тогда стандартное отклонение годовой доходности можно определить, умножив стандартное отклонение квартальной доходности на 2 или стандартное отклонение месячной доходности на 3,46. Каждый раз, когда продавец или брокер пытается продать вам какую-либо ценную бумагу, узнайте у него величину стандартного отклонения годовой доходности (или ожидаемую величину отклонения, если идет речь о первичном размещении). Если ответа нет, даже не думайте о покупке. Если вашему брокеру незнакомо понятие стандартного отклонения доходности, найдите другого.

Что в действительности означает стандартное отклонение? Оно означает, что две третьих всего времени годовая доходность актива будет находиться между одним стандартным отклонением выше и одним стандартным отклонением ниже среднего значения. В случае с активом «А» это означает, что две третьих всего времени этот показатель будет находиться между значениями –1,46 % (10 минус 11,46) и 21,46 % (10 плюс 11,46). На рис. 1.2 я изобразил обратную сторону актива «А». Можно видеть, что существует один шанс из шести получить убыток, превышающий 1,46 %. Существует один шанс из 44 получить убыток, превышающий 12,92 % (на два стандартных отклонения меньше среднего), и один шанс из 740 получить убыток, превышающий 24,38 % (на три стандартных отклонения меньше среднего).

Математические подробности: другие меры риска
Те из вас, кто имеет серьезную математическую подготовку, осознают ограничения использования стандартного отклонения (SD, от standard deviation) как меры риска. Например, в реальном мире инвестиций доходности не следуют модели классического «нормального распределения», а гораздо ближе подходят к логарифмически-нормальному распределению. Далее, существует некоторая степень асимметричности относительно среднего значения (асимметрия), а также более высокая частота событий ближе к экстремумам диапазона (эксцесс). Наиболее значимый недостаток стандартного отклонения как меры риска в том, что одинаково важное значение придается доходностям выше и ниже среднего, в то время как только события, происходящие ниже среднего значения, важны при измерении риска инвестиций. Это навело некоторых ученых и практиков на мысль ввести полудисперсию, или среднее отклонение событий, происходящих ниже среднего значения, как более реалистичное измерение риска. Однако на практике как дисперсия, так и полудисперсия дают очень похожие результаты, и дисперсия / стандартное отклонение остается превосходной мерой риска. По сути, простая дисперсия / стандартное отклонение имеет дополнительное преимущество, дважды давая возможность поймать избыточную волатильность. В печально известном случае с компанией Long Term Capital Management она едва не оказалась на грани банкротства из-за того, что ей не удавалось достичь значительной отрицательной полудисперсии. Обычный расчет показателя стандартного отклонения / дисперсии ежемесячной доходности предупредил бы о надвигающихся проблемах за несколько лет.
Определений риска существует так же много, как и ученых в области финансов. В число возможных мер риска входят вероятность номинального убытка, или убытка с поправкой на инфляцию, «стандартное отклонение убытка», или вероятность получения более низкой доходности, чем по какому-либо индексу (например, S&P 500) или по казначейским векселям. Большинство отдает предпочтение мере, связанной с вероятностью того, что доходность инвестиций окажется ниже доходности безрискового актива, обычно казначейских векселей. Это легко рассчитать, используя кумулятивную функцию стандартного нормального распределения, подобную функции биноминального распределения, которую использовал наш воображаемый профессор статистики.
Вы можете придумать собственную меру риска. Такие индивидуальные меры риска и доходности называются функциями полезности.

Рис. 1.2. Распределение доходности актива «А»

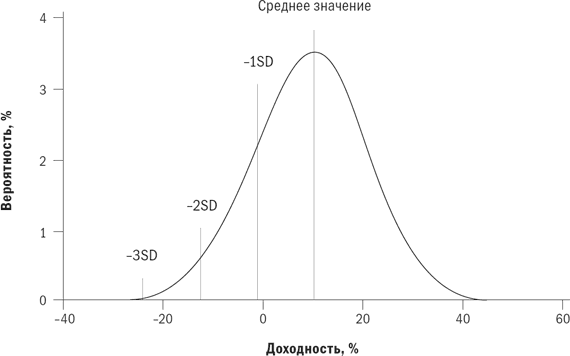
В качестве более простого примера рассмотрим фонд, состоящий из акций латиноамериканских компаний, с ожидаемой доходностью в 15 % и очень высоким стандартным отклонением в 35 %. Это сигнализирует о вероятности убытка в 20 % или выше каждые шесть лет, убытка выше 55 % каждые 44 года и убытка выше 90 % каждые 740 лет. Очень сомневаюсь, что кто-либо из торговых агентов фонда или брокеров, продвигающих подобные фонды, в последние годы сообщал такую информацию своим клиентам. По сути, одним из характерных признаков сильно перекупленного рынка является общая недооценка рисков.

Если до сих пор вы понимали весь материал этой главы, то вы либо очень старались, либо хорошо оперируете числами (или прослушали курс статистики). Сегодня больше не читайте – отложите книгу, отдохните, займитесь другими делами. В следующий раз начнем с вами рассматривать реальные активы.

Назад: 1. Общие положения

Дальше: 2. Риск и доходность