Спиралью называется плоская кривая, описываемая точкой, удаляющейся от центра при совершении кругового движения в плоскости чертежа вокруг центра спирали. На практике различают спирали с постоянным и постепенно возрастающим расстоянием между завитками. Обычно спирали строят по точкам и вычерчивают с помощью лекала.

Для того чтобы расчертить спираль, необходимо наметить не менее двух ее центров. Если вычерчивают спираль из трех или более центров, то обычно центрами спирали являются вершины правильного треугольника или правильного многоугольника. Каждую дугу проводят из последующей вершины до пересечения с лучом из угла треугольника или многоугольника. Радиус при этом каждый раз увеличивается на длину, равную длине стороны треугольника или многоугольника.

Рассмотрим, например, как начертить так называемую «архимедову спираль» (рис. 17, а). Для этого нужно провести горизонтальную линию и отметить на ней две точки О1 и О2, отстоящие одна от другой примерно на 3 мм. Поставив ножку циркуля в одну из этих точек (О1), проведите дугу радиусом 3 мм (R1), равную половине окружности. Концы этой дуги должны опираться на горизонтальную ось (в данном примере – сверху).

Затем перенесите ножку циркуля во вторую из отмеченных точек и увеличьте его раствор так, чтобы карандаш попал в конец первой дуги. Снова проведите половину окружности радиусом R2, опирающуюся на горизонтальную линию, но уже с противоположной стороны (снизу). Таким же образом, переставляя ножку циркуля то в первую, то во вторую точку и каждый раз увеличивая его раствор, продолжайте разворачивать спираль. На рис. 17, а, изображено четыре полных оборота.

Для построения спирали, имеющей три центра (рис. 17, б), находящихся на равных расстояниях один от другого, необходимо предварительно построить равносторонний треугольник 1–2–3 (заштрихован) и продолжить его стороны так, как это показано на рисунке (линии 1–1’, 2–2’ и 3–3’).

Из центра 1 проводим дугу 3–1’ радиусом R1, равным длине стороны треугольника, до пересечения с продолжением стороны 1–1’. Затем из центра 2 описываем дугу радиусом R2 = 2R1 до пересечения с продолжением стороны 2 (линия 2–2’). После этого из центра 3 проводим дугу радиусом R3 = 3R1 до пересечения с продолжением стороны 3 (линия 3–3’) в точке 3’. После этого возвращаемся в центр 1 и продолжаем построение в такой же последовательности, каждый раз увеличивая радиус дуги на величину стороны треугольника.

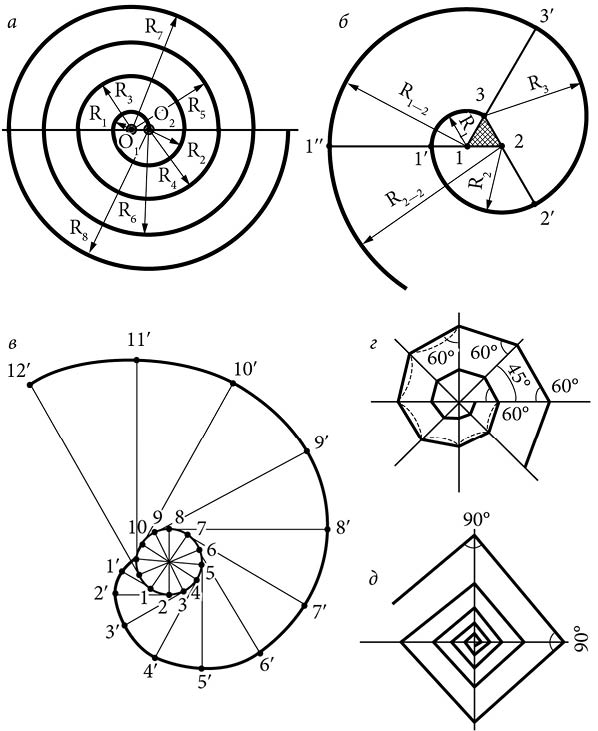
Рис. 17. Построение спиралей: а – «архимедова спираль» с двумя центрами; б – трехцентровая спираль; в – эвольвента круга; г, д – ломаные (хордовые) спирали.

Аналогично выполняют спирали с четырьмя, пятью и т. д. центрами.

Эвольвента круга (рис. 17, в) – это плоская кривая, образуемая точкой на прямой, которая перемещается без скольжения по неподвижной окружности заданного радиуса. Эта кривая иногда называется разверткой окружности. Построение эвольвенты начинается с деления заданной окружности на произвольное число равных частей, например 12. В каждой точке деления проводим касательные к окружности. На каждой из этих касательных последовательно откладываем длину окружности, равную πd/12: в точке 1 – πd/12, в точке 2 – 2πd/12, в точке 3 – 3πd/12 и т. д. На касательной к точке 12 откладываем длину окружности, равную πd. Соединяя последовательно плавной кривой по лекалу полученные на касательных точки 1’, 2’, 3’ и т. д., получим кривую, называемую эвольвентой.

Схема построения ломаных спиралей показана на рис. 17, г, д. Они строятся так же, как и циркульные, но дуги заменяются соответствующими хордами.