Главной задачей в поисках художественного образа или идеи являются размеры и пропорции. Говоря о пропорциях (соотношении размерных величин), мы учитываем их в формате плоского изображения (картина, маркетри), в соотношениях габаритных размеров (длина, высота, ширина) объемного предмета, в соотношении двух различных по высоте или длине предметов одного ансамбля, в соотношении размеров двух явно выделяющихся частей одного и того же предмета и т. д.

В классике изобразительного искусства на протяжении многих веков прослеживается прием построения пропорций, называемый золотым сечением, или золотым числом (этот термин ввел Леонардо да Винчи). Принцип золотого сечения, или динамичной симметрии, заключается в том, что отношение между двумя частями единого целого равно отношению его большей части к целому (или соответственно целого к большей части).

Математически это число получают с помощью формулы (√5+1)/2, что в результате дает 1,6180339… или, после округления, 1,62. Это число означает соотношение большей величины в пропорции к ее меньшей величине. Более точно это отношение выражается следующим образом: 5:3, 8:5, 13:8, 21:13 и т. д., или 2,2:3, 3:5, 5:8,8 и т. д.

В графике золотое сечение выражается соотношением отрезков, которые получаются при различных построениях. Простое и удобное построение в золотом сечении показано на рис. 11, а: если к диагонали полуквадрата добавить его короткую сторону, то получится величина в отношении золотого числа к его длинной стороне.

Пропорция двух величин золотого сечения создает зрительное ощущение гармонии и равновесия. Есть и другое гармоничное соотношение двух смежных величин, выражаемое числом 1,12. Оно является функцией золотого числа: если взять разность двух величин золотого сечения, разделить ее также в золотой пропорции и каждую долю добавить к меньшей величине исходного золотого сечения, то получится число 1,12 (рис. 11, б). В таком соотношении часто расположены «полочки» (средние элементы) в написании букв, например Н, Р, Я, А и др., используются пропорции высоты и ширины для широких букв. Это отношение повсеместно встречается и в природе.

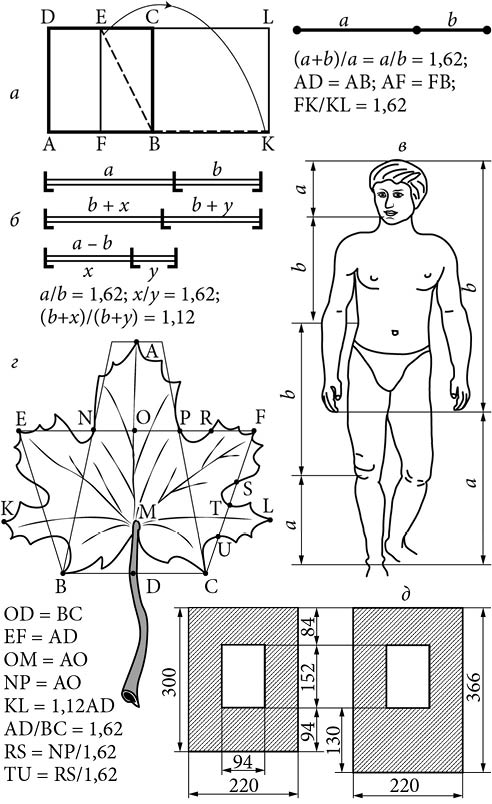
Рис. 11. Применение золотого сечения: а – геометрическое построение прямоугольника в золотом сечении 1,62: 1 и золотое число 1,62 в отношении отрезков а и b; б – графическое построение функции золотой пропорции 1,12: 1; в – золотые пропорции строения гармонично развитого человеческого тела; г – построение кленового листа; д – рамки, построенные по различным закономерностям.

Золотое число наблюдается в пропорциях строения тела гармонично развитого человека (рис. 11, в): длина головы делит в золотом сечении расстояние от талии до макушки; коленная чашечка также делит расстояние от талии до подошвы ног; кончик среднего пальца вытянутой вниз руки делит в золотой пропорции весь рост человека; отношение фаланг пальцев – тоже золотое число. Это же явление наблюдается и в иных конструкциях природы: в спиралях моллюсков, в венчиках цветков и др.

В резьбовых орнаментах растительные мотивы, особенно изображения листьев, – наиболее популярные элементы. Все листья, как правило, выполняются в пропорциях золотых чисел 1,62 и 1,12. Для примера на рис. 11, г, представлено строение листа клена. При соотношении ширины к длине в 1,12 лист имеет несколько пропорций с числом 1,62. Это так называемая десятка гармоничных пропорций кленового листа: AD/BC = EF/BC = EF/OD == OD/OM = OD/AO = OM/MD = BC/NP = NP/RS = RS/TU == 1,62; KL/AD = 1,12.

За основу построения такого листа взяты две трапеции, у которых отношение высоты и длины основания выражается золотым числом. Строение листа может быть описано такими основными соотношениями: OD = BC; EF = AD; OM = AO; NP = AO; KL = 1,12AD; AD/BC = 1,62; RS = NP/1,62; TU = RS/1,62.

Варианты поиска гармоничной пропорции можно рассмотреть на примере рамки (рис. 11, д). Внешние размеры рамки (изображенной слева) золотой пропорции не дадут: отношение ее длины и ширины (330 × 220) несколько меньше золотого числа, а именно равно 1,5, а ширина поперечных звеньев (84 и 94) соответственно увеличена по сравнению с боковыми сторонами (63). Но это позволяет выйти на размеры помещенной в рамку картины, дающие пропорции золотого сечения (152 × 94). Отношение же ширины нижнего звена рамки (94) к ширине ее верхнего звена (84) подогнано к другому золотому числу – 1,12. Кроме того, отношение ширины нижнего звена (94) к ширине бокового (63) близко к 1,5.

Таким образом, удалось сохранить пропорции картины, формата рамки и ее элементов приближенными к классической гармонии.

Если же длинную сторону рамки увеличить до 366 мм за счет ширины нижнего звена (130), то отношение внешних размеров рамки (366/220) и отношение поперечных звеньев (130/84) будет приближено к золотому числу 1,62 вместо 1,12. В результате получится новая композиция (рамка, изображенная справа), которая может быть применена в каком-либо ином изделии, но для рамки возникает желание сделать ее короче. Закройте ее нижнюю часть линейкой настолько, чтобы глаз «принял» получившуюся пропорцию, и мы получим длину 330 мм, то есть вернемся к исходному варианту.