Джеймс Клерк Максвелл, живший в XIX веке, придумал замечательный мысленный эксперимент, при помощи которого можно было бы найти лазейку во Втором законе термодинамики. Максвелл представил себе емкость, наполненную молекулами газа, и быстрыми, и медленными, основательно перемешанными, так что достигнуто состояние высокой энтропии. В середине емкости есть перегородка, отделяющая левую половину от правой, а в перегородке – малюсенькая дверца. Каждый раз, когда с левой стороны коробки к дверце приближается холодная молекула (то есть молекула, которая движется со скоростью меньше средней), очень умный демон открывает дверцу и пропускает молекулу в правую сторону емкости. Точно так же, когда справа приближается горячая молекула, демон открывает дверцу и пропускает молекулу в левую сторону емкости. В остальное время дверца закрыта.

Казалось бы, все очень просто, однако если бы такое было возможно, нам никогда больше не пришлось бы потратить ни цента на кондиционеры. Демон, не покладая рук, трудится над тем, чтобы в емкости с одной стороны было жарко, с другой холодно – совсем как в «Макдоналдсе».

Впервые я столкнулся с этой задачей, когда учился на старших курсах, и она не произвела на меня ни малейшего впечатления. Молекула туда, молекула сюда – кому это интересно? Кроме того, Второй закон термодинамики по природе своей статистический – так зачем вообще искать в нем лазейку, какой в этом смысл?

Еще какой, мой юный я. Еще какой.

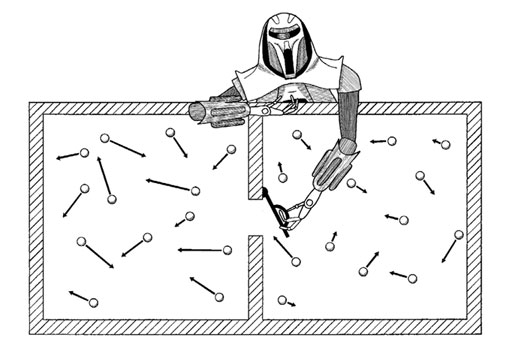
Вспомним, как должен действовать Второй закон: тепло обязано перетекать из жарких областей в прохладные. Для этого и учебник физики, пожалуй, не нужен. Большинство энергии, питающей наши машины, уходит в тепло, вот почему нам нужно постоянно жечь уголь, бензин и природный газ. Если бы мы могли нанять несколько миллионов демонов Максвелла, чтобы превращать тепло обратно в полезную энергию, у нас были бы вечные двигатели!

Я получил вполне достаточно писем от физиков-любителей, где излагались теории, грозившие, по мнению создателей, перевернуть все наши представления о вселенной. Сразу отбрасывать любые гипотезы и проекты, опровергающие Второй закон или предполагающие вечный двигатель – стандартная процедура. А вот Максвеллу положено послабление. Может быть, он и в самом деле открыл потайную дверь к тому, чтобы как-то снизить энтропию во вселенной. Если вы больше не в силах пребывать в напряженном ожидании развязки, не волнуйтесь: Второй закон цел и невредим, но чтобы понять, почему, придется залезть в голову демону.

В 1948 году Клод Шеннон, исследователь из лабораторий Белла, основал научную отрасль под названием «теория информации». Подобно тому как квантовая механика сделала физически возможным существование современной вычислительной техники, теория информации произвела переворот в криптографии и коммуникациях и сделала возможными новаторские решения вроде Интернета.

Один из главных результатов теории информации состоит в том, что информация тесно взаимосвязана с энтропией. Подобно тому, как энтропия газа описывает количество способов, какими молекулы можно переставить, информация сигнала описывает количество разных посланий, которые можно передать.

Представим себе, что я отправляю послание длиной ровно в две буквы. В принципе, поскольку в английском алфавите 26 букв, я мог бы передать вам 26 × 26 = 676 разных посланий, однако большинство подобных буквосочетаний совершенно бессмысленны. Двухбуквенных слов совсем немного (в словаре для игры в «Скрабл» их 101).

Если среди вас есть специалисты по информатике, отмечу, что это значит, что хотя в принципе для дифференциации всех возможных комбинаций из двух букв потребуется около 10 бит (единиц и нулей, используемых для хранения данных), если вы знаете, что передаете слово, достаточно всего 7 бит. Экономия!

Коммуникацию можно значительно сократить, если отметить, что некоторые буквы используются гораздо реже прочих. Например, в английском языке Е встречается значительно чаще, чем Z. Если играешь в «виселицу», простое знание, что в слове есть Z, резко сокращает число вариантов. Вот почему Е в «Скрабле» стоит всего одно очко, а Z – целых десять, и вот почему Е в азбуке Морзе обозначается ., а Z – . ..

Отстучать Z занимает заметно больше времени, но это не страшно, потому что это приходится делать гораздо реже. Чем сложнее (или непредсказуемее) послание, тем больше информации в нем содержится и тем больше байтов данных потребуется, чтобы хранить его в компьютере.

Что заставляет нас вернуться к демону Максвелла. Давайте уберем из уравнения нейрофизиологию и предположим, что Демон на самом деле какой-то фантастический робот, который хранит свои данные в цифровом виде. Компьютерная память – это последовательность нулей и единиц. Неважно, есть у нас на диске файлы или нет, главное – что существует конечное количество разных комбинаций нулей и единиц, которые можно хранить. Какое именно это число, можно подсчитать, если умножать 2 × 2 × 2… – по двойке на каждый бит на диске. Чем больше битов, тем больше разных комбинаций.

Каждый раз, когда демону надо решить, пропускать ли в дверцу очередную молекулу, он измеряет ее скорость и записывает результат. А теперь предположим, что у него есть особый диск, очень маленький, отведенный исключительно для того, чтобы хранить запись скорости молекулы до тех пор, пока не будет принято решение, пропускать ли ее в дверцу. В начале эксперимента все регистры на диске стоят в положении «ноль» – конфигурация с очень низкой энтропией.

С другой стороны, если диск наполнен случайным на вид набором нулей и единиц, там либо содержится уйма информации, либо набор действительно случаен и это просто высокий уровень энтропии.

Однако наш демон начинает с чистого листа.

К дверце подлетает первая молекула, демон измеряет ее скорость, прилежно сохраняет данные на диск и решает пропустить молекулу. Подлетает вторая молекула, но тут – вот досада! – диск оказывается полностью забит данными первого измерения. У демона не остается выхода: приходится стереть первую запись, прежде чем можно будет продолжать работу, и именно тут мысленный эксперимент Максвелла терпит полный крах.

В 1961 году специалист по информатике Рольф Ландауэр сделал одно примечательное наблюдение: если уничтожаешь бит информации, обязательно создаешь эквивалентное количество энтропии во вселенной. Создание и последующее уничтожение записей о движении молекул высвобождает по крайней мере столько же энтропии, сколько демон, как предполагалось, экономил, когда распределял молекулы по скорости. Играя в свои игры с газом, демон на самом деле не снижал общую энтропию во вселенной. Он ее просто перераспределял.

Прежде чем двигаться дальше, стоит посвятить еще несколько минут устройству памяти демона. Мы исходим из предположения, что когда он измеряет скорость молекул или еще что-нибудь, то начинает с чистого листа – то есть, возможно, из конфигурации из всех нулей. Но что если не исходить из такого предположения?

Очевидно, среди всех возможных конфигураций памяти есть некие особые, незаурядные конфигурации. Примерно как буквы в «Скрабле»: про большинство комбинаций из нулей и единиц сразу понятно, что они яйца выеденного не стоят, но все равно можно случайно вытянуть из мешочка буквы, из которых составится настоящее слово. Беда в том, что сгенерированная случайным образом (но при этом в целом осмысленная) последовательность букв на доске выглядит точь-в-точь как настоящее слово, которое кто-то преднамеренно выставил.

Если вы найдете жесткий диск, полный случайных на вид нулей и единиц, то с полным правом предположите, что все эти биты – это настоящие данные, записанные на диск. Подобным же образом, если бы вы были роботом, который прочитал диск и обнаружил сложную последовательность чисел, вы бы предположили, что это настоящие данные. С точки зрения робота, данные на диске – это в точности то же самое, что память, и нет никакой разницы между настоящей памятью, которая сформировалась благодаря опыту, и памятью, которая сформировалась в результате процессов, эквивалентных вытягиванию из мешка случайных фишек с буквами.

Иными словами, мы в целом предполагаем, что любые сложные последовательности, которые записаны у нас в мозгу, на доске для «Скрабла» или в физике вселенной, так или иначе представляют собой точное отражение каких-то реальных событий в прошлом.

Философ Дэвид Альберт выдвинул «Гипотезу прошлого» как предположение, что в прошлом энтропия была ниже, чем в настоящем. Если бы мы имели дело с компьютером, это означало бы, что мы начинаем с обнуления всех регистров, а потом добавляем данные. Если «Гипотеза прошлого» верна, то информация, закодированная в памяти – это реалистическая интерпретация произошедшего в прошлом. Если бы запись на диске компьютера начиналась с состояния высокой энтропии, у нас не было бы ни малейшего представления о том, что там настоящие воспоминания, а что – шум. Чтобы хоть как-то разбираться в прошлом, нам придется предположить, что и мы сами, и вселенная в более широком смысле в начале своего существования пребывали в состоянии крайне низкой энтропии.

А это подводит нас к крайне болезненному вопросу о ранних этапах существования вселенной…