Если заряженная частица помещена в электрическое поле, она под действием этого поля начнет двигаться. Направление движения будет определяться направлением электрического поля и знаком электрического заряда. При этом протоны и электроны двигаются в противоположных направлениях. Возникает электрический ток, направление которого чисто условно принято считать обратным направлению движения электронов (т. е. совпадающим с направлением движения протонов). Для того чтобы рассчитать величину этого электрического тока, надо величину электрического поля умножить на проводимость среды, в которой ток течет. Как известно, проводимость твердых или жидких веществ отличается от проводимости газов. Нас интересуют газы, а точнее, частично ионизованная плазма, в которой только часть атомов и молекул ионизована.

Такая относительно простая картина имеет место в случае плазмы, помещенной в электрическое поле. Ситуация сильно усложняется, если на эту плазму с электрическим полем «наложить» еще и магнитное поле.

Так, если без магнитного поля электроны и протоны двигались в противоположных направлениях и создавали электрический ток, то в присутствии магнитного поля при действии того же электрического поля электроны и протоны начнут перемещаться в одном и том же направлении. При равенстве их концентраций это движение не будет представлять собой электрического тока, поскольку суммарный перемещающийся электрический заряд равен нулю. Кроме того, в присутствии магнитного поля заряженные частицы перемещаются не вдоль (или против) направления электрического поля, а поперек этих полей, но в случае, если оба эти поля перпендикулярны друг другу.

В отсутствии магнитного поля мы говорили просто о проводимости плазмы (ионизованного газа). В присутствии же магнитного — мы должны говорить о нескольких типах проводимости: вдоль магнитного поля, поперек него и т. п. Электрически заряженным частицам отнюдь не одинаково легко двигаться в этих направлениях. Другими словами, среда, которая до наложения магнитного поля была изотропной, т. е. ее свойства не зависели от направления, после наложения становится анизотропной.

Вся проблема солнечно-земной физики связана с частично или полностью ионизованной плазмой, помещенной в магнитное поле (магнитное поле солнечных пятен, межпланетное магнитное поле, магнитное поле Земли). Причем на эту плазму действуют различные силы (силовые поля): электрическое поле, силы притяжения и силы, связанные с градиентами давления, градиентами и конфигурацией магнитного поля и т. п. Поэтому необходимо проанализировать, как же движутся заряженные частицы в таких ситуациях.

Рассмотрим возможные варианты.

1. Электрически заряженная частица движется вдоль магнитного поля. Легко показать, что в этом случае она не чувствует его наличие и движется так же, как и в его отсутствии. Это благоприятные условия для движения заряженных частиц. Поскольку силовые линии магнитного поля Земли почти вертикальны в высоких широтах в обоих полушариях, то это и создает благоприятные условия для осаждения (соскальзывания) заряженных частиц в атмосферу этих широт. В низких широтах и на экваторе частицам пришлось бы прорываться поперек силовых линий магнитного поля Земли, а это для частиц с энергиями, при которых они вызывают полярные сияния, непреодолимо трудно.

2. Заряженные частицы движутся поперек магнитного поля. В этом случае на частицу начинает действовать сила (рис. 10), которая норовит закрутить ее вокруг силовой линии магнитного поля (сила Лоренца). Как только траектория частицы закручивается, начинает действовать центробежная (направленная от центра кривизны) сила, прямо пропорциональная массе и квадрату скорости частиц (их произведению) и обратно пропорциональная радиусу кривизны траектории частицы. Движение будет установившимся, если эти силы уравновесятся. Из их равенства получим, что радиус окружности, по которой будет вращаться частица (так называемый радиус Лармора) равен

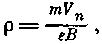
а угловая скорость ω и период вращения Т при этом равны

где е — величина электрического заряда частицы, m - масса частицы, V_n — скорость частицы поперек магнитного поля, В — величина магнитного поля.

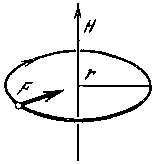
Рис. 10. Направление силы Лоренца при движении частицы перпендикулярно магнитному полю

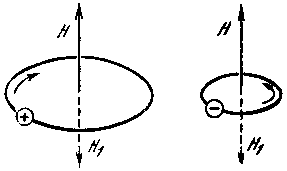
Рис. 11. Направление вращения положительно и отрицательно заряженных частиц вокруг силовой линии магнитного поля H

H₁ — магнитное поле, создаваемое движущимся электрическим зарядом

 

Отсюда следует, что заряженные частицы, которые не движутся строго вдоль силовых линий магнитного поля Земли, будут вращаться вокруг силовых линий (рис. 11). В одном и том же магнитном поле одной и той же скорости движения радиус протонов почти в 2000 раз больше радиуса электронов, т. е. ровно во столько раз, во сколько раз отличаются их массы (1840 раз). Это весьма существенно для физики околоземного пространства. Круговая частота вращения для электронов и протонов также зависит от их массы, только уже не прямо, а обратно пропорционально. Частота вращения протонов (гирочастота) в 1840 раз меньше гирочастоты электронов. Гирочастоты входят в выражения для проводимостей, значит, и в условия распространения радиоволн. Очень важно для продвижения частицы, сумеет ли она большую часть времени вращаться вокруг силовой линии (тогда она оказывается как бы привязанной к данной силовой линии), или будет часто выталкиваться при соударениях с другими частицами от одной силовой линии к другой, не успев совершить даже одного полного оборота вокруг магнитной силовой линии. Другими словами, важно соотношение частоты вращения и частоты столкновений данной частицы с другими частицами. Если частота вращения (гирочастота) много больше частоты столкновений, то частицы плазмы «вморожены» в магнитное поле.

3. Заряженная частица движется под определенным углом к направлению магнитного поля. Этот угол называется питч-углом. Это движение всегда можно разложить па две составляющие — поперек магнитного поля и одновременно вдоль магнитного поля. Оба эти случая мы выше рассмотрели. Применив описанные выше результаты к этому более общему случаю, получим, что частица, которая имеет составляющие скорости движения и вдоль и поперек магнитного поля одновременно, движется по спирали, накручиваясь на магнитную силовую линию (рис. 12). Шаг спирали будет зависеть от величины продольной скорости, а величина радиуса — от величины поперечной энергии частицы, которая при заданной массе определяется поперечной к магнитному полю скоростью частицы.

4. Заряженная частица движется в магнитном поле и на нее одновременно действует также электрическое поле. В этом случае электрическое поле добавляет частице скорость поперек магнитного поля и одновременно поперек электрического (рис. 13). Величина этой скорости зависит прямо пропорционально от величины последнего и обратно пропорционально от величины первого. Направление дрейфового движения не зависит от знака электрического заряда. Картина движения в этом случае выглядит так: электроны и протоны вращаются по спиралям вокруг магнитных силовых линий в обратных направлениях с разными радиусами и угловыми частотами. Одновременно и те и другие (под действием электрического поля) дрейфуют в одном и том же направлении с одной и той же дрейфовой скоростью (которая не зависит ни от заряда, ни от массы и скорости частицы) поперек как магнитного, так и электрического поля, которые, в свою очередь, перпендикулярны друг другу. Такую картину мы наблюдаем в хвосте магнитосферы, где на магнитное поле Земли наложено крупномасштабное электрическое поле, направленное с утренней стороны на вечернюю.

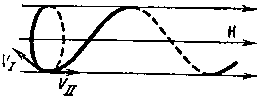
Рис. 12. Движение заряженной частицы по спирали вокруг силовых линий магнитного поля

 

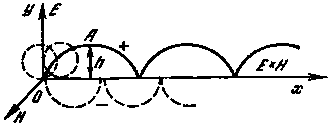
Рис. 13. Движение заряженных частиц в скрещенных полях по циклоидам

Электрическое поле направлено снизу вверх

 

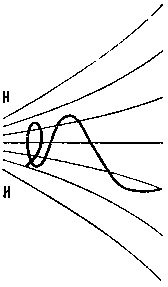
Рис. 14. Траектория заряженной частицы, двигающейся в сторону возрастающего магнитного поля Н

 

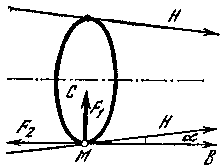
Рис. 15. Силы, действующие на частицу в магнитном поле со сходящимися силовыми линиями:

F₁ — поддерживает ларморовское вращение; F₂ — выталкивает частицу в сторону ослабевающего поля

 

5. Заряженная частица движется в неоднородном магнитном поле. Другими словами, магнитное поле имеет градиент, т. е. изменяется от одной точки пространства к другой.

Если частица движется по спирали вокруг силовой линии магнитного поля, которое по мере продвижения частицы увеличивается (т, е. силовые линии сходятся), то по мере увеличения магнитного поля она замедляет свое поступательное движение вдоль силовой линии (рис. 14) и при определенном поле отразится и будет продолжать двигаться в обратном направлении, т. е. в сторону уменьшения магнитного поля (рис. 15). В магнитосфере силовые линии магнитного поля сходятся по мере их приближения к поверхности Земли в высоких широтах. Поэтому электроны и протоны, вращаясь вокруг таких силовых линий по спиралям и подходя к местам сгущения силовых линий, отражаются и направляются в другое полушарие (рис. 16). Там они так же отражаются и движутся обратно в прежнее полушарие. Так происходит до тех пор, пока по какой-либо причине они не попадут в область плотной атмосферы, где в соударениях с нейтральными частицами потеряют свою энергию. Такая критическая ситуация может создаться во время геомагнитной бури, когда нарушается структура силовых линий.

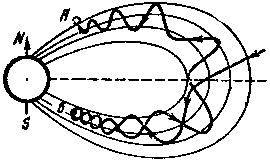
Рис. 16. Движение заряженной частицы в магнитном поле Земли (в меридиональной плоскости)

А и Б — точки отражения или зеркальные точки

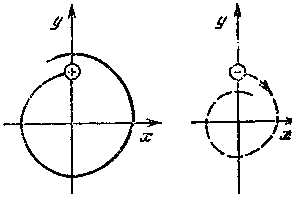
Рис. 17. Дрейф заряженных частиц, двигающихся в неоднородном магнитном поле в плоскости, перпендикулярной к H

 

Кроме описанного явления, в неоднородном магнитном поле заряженная частица приобретает дрейфовую скорость, перпендикулярную магнитной силовой линии и одновременно направлению наибольшего изменения магнитного поля, т. е. градиента поля (рис. 17). В случае магнитного поля Земли электроны начнут дрейфовать на восток, а протоны — на запад, поскольку градиент магнитного поля направлен по радиусу. В отличие от дрейфа за счет действия электрического поля, когда электроны и протоны дрейфуют вместе, т. е. в одном направлении и с одинаковой по величине скоростью, дрейф электронов и протонов за счет градиента геомагнитного поля создает электрический ток; направление их дрейфа противоположно. Именно этому дрейфу обязан своим происхождением кольцевой ток, текущий в магнитосфере вокруг Земли и изменяющий свою интенсивность в зависимости от поступления заряженных частиц.

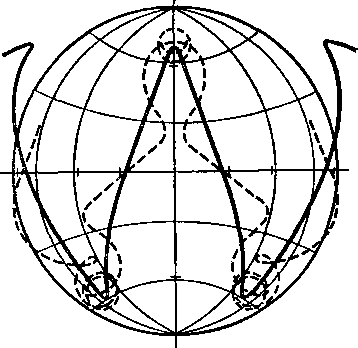
Рис. 18. Схематическое изображение траектории заряженной частицы в магнитном поле Земли

 

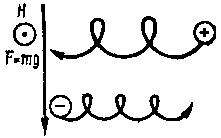
Рис. 19. Дрейф частиц в поле тяжести, перпендикулярном к магнитному полю Н

 

Магнитное поле Земли неоднородно не только в радиальном направлении, его силовые линии изогнуты — они выходят из южного полушария и входят в северное, удаляясь на самое большое расстояние от Земли в экваториальной плоскости. Этот факт также отразится на движении заряженных частиц. В результате электроны и протоны будут дрейфовать в противоположных направлениях (восток—запад). Это движение также приводит к образованию электрического тока (рис. 18).

Полученные выше результаты можно приложить к любой действующей на частоту силе. В частности, такой может быть сила земного притяжения, под действием которой заряженные частицы дополнительно приобретают скорость дрейфа, направленную поперек этой силы и одновременно поперек силовым линиям магнитного поля (рис. 19). Это движение также порождает электрический ток, поскольку электроны и протоны (положительные ионы) дрейфуют в противоположных направлениях.

Подведем итог возможных ситуаций в околоземном космическом пространстве. Заряженные частицы вращаются вдоль магнитных силовых линий и одновременно смещаются вдоль силовой линии, т. е. движутся по спиралям. Попадая в области более интенсивного магнитного поля, они отражаются и, продолжая двигаться по спирали, дрейфуют в противоположное полушарие. Затем, отразившись и там, снова возвращаются и т. д. За счет неоднородности геомагнитного поля одновременно с описанным движением, частицы постепенно дрейфуют от одной силовой линии к другой в направлении восток—запад. Этот азимутальный дрейф создает электрический ток, окружающий Землю.

Законы движения заряженных частиц в геомагнитном поле состоят в сохранении трех физических величин: магнитного момента частицы, интеграла действия вдоль силовой линии и магнитного потока через оболочку. Движение заряженных частиц по окружности (вокруг силовой линии магнитного поля) эквивалентно круговому току. Магнитное поле этого кругового тока может быть представлено как поле точечного диполя с магнитным моментом μ:

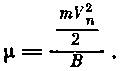
Магнитный момент определяется отношением «поперечной» кинетической энергии частицы к величине магнитного поля. Можно показать, что величина магнитного момента при движении заряженной частицы в магнитном поле остается постоянной. Другими словами, магнитный момент является адиабатическим инвариантом.

Второй, продольный инвариант I равен интегралу (сумме) действия (т. е. mV_s) вдоль силовой линии между точками отражения.

Сохранение μ и I позволяет объяснить образование пояса захваченных вокруг Земли заряженных частиц. Положим, что нам известна величина магнитного поля в данной точке на экваторе, равная B₀, угол между направлением движения частицы и этим полем в данной точке (питч-угол) α₀ и значение I для данной частицы. Рассмотрим, где может оказаться эта частица при последующем движении.

Первый инвариант дает нам, что частица всегда будет отражаться на поверхности В = В_m, которая определяется из условия (sin²α)/B = 1/B_m. Однако это еще не означает, что частица всегда будет оставаться на силовой линии, для которой значение поля на экваторе равно В₀. Первый инвариант не накладывает в этом отношении никаких ограничений, и в частности не препятствует тому, чтобы частица вследствие дрейфа изменила долготу и отразилась на экваторе, т. е. при В_т = В₀.

Второй инвариант полагает дополнительное требование на движение частицы. Она не только должна иметь точки отражения на поверхности В = В_m, но и интеграл вдоль силовой линии должен оставаться величиной постоянной. На заданной долготе это условие определяет одну единственную силовую линию, вдоль которой частица должна совершать колебания по широте. Закон сохранения второго адиабатического инварианта позволяет установить, вокруг какой силовой линии будет происходить движение частицы при ее азимутальном дрейфе.

Третьим инвариантом движения частицы является инвариант потока. Он связан с долготным азимутальным дрейфом и наиболее легко нарушается. Этот инвариант равен полному потоку вектора магнитного поля В через поверхность, ограниченную поверхностью дрейфа частицы по долготе, т. е. поверхностью одинаковых величин второго инварианта.

Все описанные инварианты в общем случае позволяют предсказать движение частицы.