Книга: Быстрая математика: секреты устного счета
Назад: Глава 13 Стандартное деление столбиком
Дальше: Глава 15 Деление посредством сложения
Глава 14
Прямое деление
Если вы легко выполняете деление на однозначные числа, то деление столбиком не должно представлять для вас труда. Если вы делите на число, не являющееся простым (то есть на число, которое может быть разложено на множители), то задача не представляет особого труда. Деление на большие числа также не должно создавать проблем, если вы используете принцип приближенной оценки посредством множителей. Ниже я предлагаю альтернативный метод, который может быть использован для деления на двузначные и трехзначные числа.
Деление на двузначные числа
Рассмотрим пример:
2590: 73 =
Прежде всего округляем 73 до 70 и будем делить на 10 и 7, делая по ходу поправку на 3, которое держим в уме.
Делим число на 10. Это переместит запятую на одну позицию влево.
2590: 10 = 259,0
Теперь делим 259,0 на 7, делая одновременно поправку на 3.
25 делится на 7 три раза (3 х 7 = 21) с остатком 4. Таким образом, 3 — это первая цифра ответа. Переносим остаток, как при обычном способе деления. Приписав 4 к следующей цифре делимого (9), получаем 49. Внесем поправку путем умножения предыдущей цифры ответа (3) на цифру единиц (3) в исходном делителе (73). Получаем: 3 х 3 = 9. Вычтем 9 из 49 и получим 40. Теперь разделим 40 на 7. В ответе получается 5, поскольку 5 х 7 = 35 (остаток 5). 5 — это вторая цифра искомого ответа. Переносим остаток к следующей цифре, после чего работаем с числом 50.
Умножим последнюю полученную цифру ответа (5) на цифру единиц в исходном делителе (3). Получаем 15. Вычитаем 15 из 50 и получаем 35. Делим 35 на 7. Имеет место деление нацело, и в ответе получается 5. Остатка у нас нет, и в связи с этим у нас возникает проблема, что переносить к следующей цифре. Уменьшаем полученный ответ на 1 и получаем 4 с остатком 7 (замечание: 4 х 7 + 7 (остаток) = 5 х 7, то есть мы просто иначе выразили одно и то же число).
Умножим 4 на цифру единиц (3) и получим 12. Вычтем 12 из 70 и получим 58. 58, деленное на 7, дает 8 с остатком 2. Перенос 2 даст нам новое число для работы: 20. Достаточно ли оно велико? Нам придется вычесть 8 х 3 = 24 из 20. Полученный ответ снова слишком большой, поэтому уменьшаем его на 1 и получаем 7. 58, деленное на 7, дает нам 7 с остатком 9. Записываем 7 и переносим 9 дальше. Получили рабочее число 90. Далее: 7 х 3 = 21 и 90–21 = 69. Это приемлемо.
Поделив 69 на 7, имеем 9 с остатком 6. 9 — это следующая цифра ответа.
После соответствующей тренировки все вычисления могут быть выполнены в уме.
Рассмотрим другой пример:
2567: 31 =
30 — это 3, умноженное на 10, поэтому делим сначала на 10, а потом на 3, внося по ходу решения поправки.
2567: 10 = 256,7
25 делится на 3 восемь раз с остатком 1. 8 будет первой цифрой нашего ответа. Остаток 1 переносится к следующей цифре делимого, что дает нам 16.
Внося поправку, умножим полученную цифру ответа на цифру единиц (1) в делителе (31). 8 х 1 = 8. Вычитаем 8 из рабочего числа 16 и получаем в ответе 8.
Теперь делим 8 на 3. В ответе получаем 2 с остатком 2. Переносим остаток 2 к следующей цифре. Новое рабочее число — 27. Нам опять требуется внести поправку.
Предыдущая цифра ответа — 2. Умножаем ее на цифру единиц исходного делителя. 2 на 1 будет 2, 27 минус 2 равно 25. Делим 25 на 3, получая в ответе 8 с остатком 1.
Умножаем последнюю полученную цифру ответа (8) на цифру единиц (1) в делителе и в ответе имеем 8. Вычтем 8 из нового рабочего числа (10). 10 минус 8 равно 2. 2 на 3 разделить нельзя. Значит, следующая цифра ответа равна 0.
Это дает нам ответ с точностью до одного знака после запятой.
Попробуйте решить следующие примеры самостоятельно. Если хотите, можете решать столбиком. Попробуйте решить некоторые примеры в уме и запишите полученный ответ.
а) 368: 71 = __; б) 236: 43 =__; в) 724: 61 = __; г) 549: 61 = __; д) 1234: 41 = __
Ответы:
а) 5,18; б) 5,488; в) 11,869; г) 9; д) 30,09756
Способ округления в сторону увеличения
Если цифра в разряде единиц в делителе велика, можно следовать видоизмененной процедуре.
Например:
2590: 69 =
Заменяем 69 на 70 — 1.
Делим на 10, а потом на 7, внося поправки по ходу.
25 делится на 7 три раза (3 х 7 = 21) с остатком 4. Приписываем 4, как и прежде, к следующей цифре делимого, что дает нам рабочее число 49. Теперь умножаем полученную цифру ответа (3) на 1, которую мы рассматриваем цифрой единиц в делителе. В ответе получаем 3. Прибавляем его к рабочему числу и получаем 52. Разделив 52 на 7, получим 7 с остатком 3. Записываем 7 и переносим 3. Получаем новое рабочее число: 30.
Теперь умножим последнюю полученную цифру ответа (7) на 1, что даст нам 7. Прибавим 7 к 30 и получим 37. 37, деленное на 7, дает 5 с остатком 2. Записываем 5 следующей цифрой и переносим 2. Получили рабочее число 20. Прибавим к нему 5 х 1 = 5 и получим 25. 25, деленное на 7, равно 3 с остатком 4. Переносим 4 и получаем новое число 40. Прибавляем к нему 3, получаем 43. 43, деленное на 7, дает 6 — это следующая цифра нашего ответа. Можно продолжать до любого количества знаков после запятой. Решение до трех знаков после запятой выглядит следующим образом:
Попробуйте решить следующие примеры самостоятельно:
а) 2671: 41 = __; б) 3825: 58 = __; в) 3825: 62 = __; г) 2536: 39 = __
Ответы:
а) 65,146; б) 65,948; в) 61,69; г) 65,0256
Если вы округляете исходный делитель в сторону увеличения, получая вспомогательный делитель, то корректирующую величину следует прибавлять к рабочему числу. Если же вы округляете исходный делитель в сторону уменьшения, то корректирующую величину следует вычитать из рабочего числа.
Запомнить, следует ли прибавлять или вычитать корректирующую величину, помогает следующий способ: представьте, что вам надо разделить 15 подарков на 9 или 11 человек. В каком случае в результате деления получится больший остаток? Если бы вы делили на 10, то вам пришлось бы прибавить 1, корректируя ответ, полученный от деления на 9. В другом же случае вы вычитали бы 1, чтобы скорректировать ответ, полученный от деления на 11.
Укажу на трудность, возникающую при использовании данного метода, и объясню, как с ней можно справиться.
Вычислим 2536: 39. Вот таким образом я записываю условие задачи:
Я записываю делитель (39), затем +1 над ним, чтобы получить наш рабочий делитель 40. (Знак «плюс» говорит о том, что необходимо прибавить 1, умноженное на последнюю полученную цифру ответа.)
Чтобы разделить на 40, делим сначала на 10, а потом на 4. 2536, деленное на 10, дает 253,6. Теперь разделим на 4, внося по ходу вычислений поправки.
25 делится на 4 шесть раз с остатком 1. Переносим 1 к следующей цифре (3), что дает нам 13.
Теперь внесем поправку. 6 на +1 дает +6. Прибавим 6 к нашему рабочему числу 13 и получим 19. 19, деленное на 4, дает 4 с остатком 3. Записываем в ответ 4 и перенесем 3, получая 36 в качестве следующего рабочего числа.
4, умноженное на +1, дает +4. 36 плюс 4 равно 40. 40, деленное на 4, будет 10.
Теперь мы столкнулись с проблемой. 10 не годится для ответа, поэтому мы делаем вывод, что предыдущая полученная цифра была слишком малой. Повышаем ее с 4 до 5.
19 делится на 4 пять раз с остатком —1.
(Иными словами, 5 х 4 = 20. 19 — рабочее число; оно равно 20 — 1.)
Когда переносим 1 к следующей цифре, эта единица представляет собой число 10. (2 представляет 20, 3 представляет 30 и т. д. Иными словами, мы умножаем переносимую цифру на 10.)
Умножим последнюю цифру ответа (5) на +1, получаем +5. Следующим рабочим числом является 1: 6 (помним о —10) плюс 5, то есть 11, минус 10.
1 делится на 4 нуль раз с остатком 1.
Следующим рабочим числом будет 10. 10 плюс 0, а затем умноженное на +1, дает 10.
10 делится на 4 два раза с остатком 2.
Наше рабочее число теперь 20. Имеем: (20 + 2) х 1 = 22.
22, деленное на 4, дает 5 с остатком 2.
Очередным рабочим числом является 20: (20 + 5) х 1 = 25.
25, деленное на 6, дает 4 с остатком 1.
10 плюс 6 равно 16. 16 при делении на 4 дает 4. Видим, что полученный ответ — 65,0256 — точен до 4 десятичных знаков.
Когда в одном месте получилось 10 в результате деления рабочего числа на рабочий делитель, мы поняли, что нужно увеличить последнюю цифру ответа на 1. Затем мы получили отрицательный остаток, подлежащий переносу, который должен, по идее, быть увеличен в 10 раз (поскольку остаток переносится из более высокого разряда). Не прибавляйте этот остаток к очередной цифре делимого вплоть до того (а точнее, не вычитайте, поскольку речь идет об отрицательном числе), как вы умножили последнюю полученную цифру ответа на корректирующий множитель и прибавили полученное число к текущей цифре делимого, так как всегда легче вычесть в конце число, кратное 10, чем вычесть его в начале, а затем работать с отрицательными числами.
Деление на трехзначные числа
Деление на трехзначное число аналогично делению на двузначное. Например:
45678: 321 =
Оформляем решение примера так же, как в случае деления на двузначное число.
321| 45678
Прежде всего делим на 300. Для этого сначала делим на 100, а потом на 3.
Деление на 100 подразумевает перенос десятичной запятой на две позиции влево. Это дает нам число 456,78.
Теперь делим на 3 и вносим поправки по ходу решения.
4 при делении на 3 дает 1 с остатком 1, поэтому 1 — это первая цифра нашего ответа. Записываем 1 под цифрой 4 делимого. Остаток 1 переносим к следующей цифре, что дает нам рабочее число 15.
Теперь умножим наш ответ (1) на вторую цифру делителя (2). 1 на 2 равно 2. Вычитаем 2 из нашего рабочего числа (15) и получаем 13. Теперь делим 13 на 3. 13 при делении на 3 дает 4 с остатком 1. 4 — это следующая цифра ответа. Переносим остаток, как обычно, и получаем новое рабочее число 16.
Теперь умножим последнюю цифру ответа (4) на вторую цифру делителя:
4 х 2 = 8
Также умножим предыдущую цифру ответа (1) на третью цифру делителя (1). Сложим эти два числа (8 + 1 = 9) и вычтем сумму из рабочего числа. Нашим рабочим числом является 16, поэтому: 16 — 9 = 7.
Разделим 7 на 3, чтобы получить следующую цифру в ответе. 7 при делении на 3 дает 2 с остатком 1.
Переносим остаток к следующей цифре (7) и получаем новое рабочее число 17.
Перемножим накрест две последние цифры ответа с двумя последними цифрами делителя. Затем сложим два полученных результата.
2 х 2 = 4
4 х 1 = 4
4 + 4 = 8
Вычтем 8 из нашего рабочего числа 17: 17 — 8 = 9. Теперь разделим 9 на 3.
Мы знаем, что нам нужен остаток для переноса к следующей цифре. Если мы ничего не перенесем, хватит ли нам величины самой цифры? Да, хватит, поскольку наше следующее перемножение цифр накрест и сложение результатов дадут в сумме 8 (8: 3 = 2 r2, затем 3 х 2 = 6, 2 х 2 = 4, 6 + 2 = 8), однако в этом случае не будет остатка для последнего шага. Поэтому уменьшим 3 до 2 и получим остаток 3.
9: 3 = 2 r3
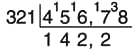
Нашим следующим рабочим числом будет 38. Перемножаем накрест, а затем складываем результаты:
2 х 2 = 4
2 х 1 = 2
4 + 2 = 6
38 — 6 = 32
Делим 32 на 3 и получаем 9 с остатком 5. (Мы намеренно занизили целую часть, поскольку нам нельзя получить 10 в качестве ответа — ответом должно быть только однозначное число.) Уже сейчас можно сказать, что нам придется вычитать достаточно большое число после перемножения накрест, поскольку одним из множителей является 9.
Наше текущее рабочее число — 50. Умножим накрест:
9 х 2 = 18
2 х 1 = 2
18 + 2 = 20
50 – 20 = 30
Делим 30 на 3 с остатком.
30: 3 = 9 r3
Очередное рабочее число — 30. Умножаем накрест.
3 не делится на 3 с остатком, поэтому следующая цифра в ответе — 0.
Прервем решение на этом месте, получив в качестве ответа число 142,2990, являющееся точным до четвертого знака после запятой. Можно продолжить до любого знака, какого пожелаете.
Разве данный способ не проще стандартного деления в столбик?
Вот несколько примеров для самостоятельного решения:
Попробуйте решить свои собственные примеры, проверяя ответы с помощью калькулятора. В главе 16 мы познакомимся с методом для простой и быстрой проверки того, правильно ли мы решили задачу на деление.
9 х 2 = 18
9 х 1 = 9
18:9 = 27
30 – 27 = 3
а) 7120: 312 = __; б) 4235: 213 = __
Ответы: а) 22,82; б) 19,88

