Книга: Лаборатория химических историй. От электрона до молекулярных машин
Назад: Ион металла все упростил
Дальше: От химии к механике
Топология – «пластилиновая» наука
Сравнивая два соединения, химики прежде всего обращают внимание на то, из каких атомов собрана молекула и в каком порядке они расположены. При переходе к катенанам подход изменяется: в первую очередь нужно понять, каким образом заплетены фрагменты молекул. Существует катенан, который долгое время не удавалось синтезировать. Это молекула, состоящая всего из двух циклов, при этом дважды переплетенных. Исторически эту фигуру называют «узел Соломона», несмотря на то что это не узел, а два сплетенных кольца. Такие кольца встречаются в качестве элементов узора уже в древнеримских мозаиках (рис. 3.9а). Саваж сумел получить такое соединение (рис. 3.9б), а спустя некоторое время подобный катенан синтезировал испанский химик Х. М. Кинтела, при этом методика синтеза и состав соединения были совсем другие (рис. 3.9в). Очевидно, что состав этих двух соединений различен, но непросто установить сходство в особенностях переплетения фрагментов, тем более что авторы изобразили обобщенную структуру различными способами. И все же способ сплетения одинаков. Существуют специальные приемы, позволяющие это установить: например, можно двигаться по отдельному кольцу и считать число переплетений, встречающихся на пути. Можно сделать одну фигуру из двух пластилиновых колец, а затем, аккуратно передвигая отдельные части, превратить ее во вторую фигуру или проделать то же самое с веревкой.
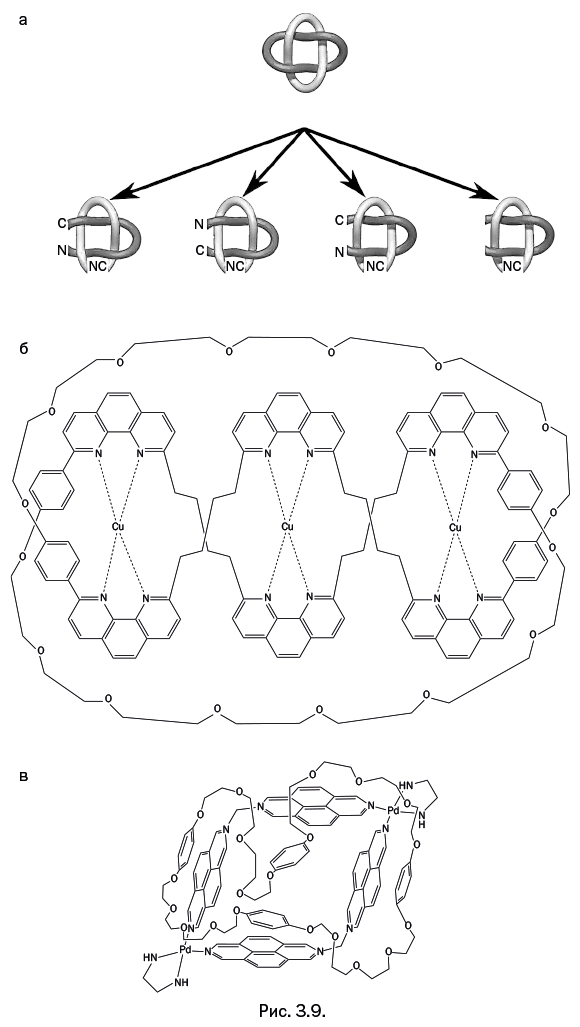
Итак, это двойные катенаны, и важно то, что оба соединения топологически эквивалентны. Рассмотрим подробнее термин «топологический».
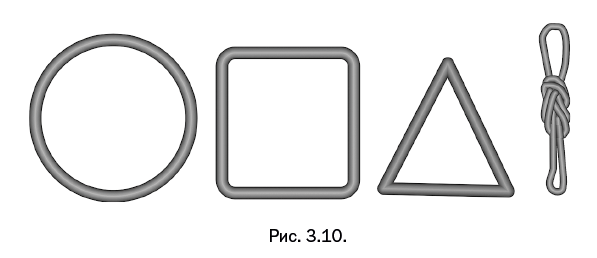
Топология изучает свойства различных фигур и объемных тел, которые не изменяются при различных деформациях. Рассматриваются только такие деформации, которые не нарушают целостность поверхности – то есть не образуют новых отверстий – и не устраняют имеющиеся. Топологию находят необычайно интересной люди, которым нравится решать задачи, требующие пространственного воображения. Предположим, мы имеем эластичный резиновый шнур в форме кольца. Расположим его на столе в виде окружности. Разрешаются любые деформации шнура, нельзя только его разрывать. Разнообразные деформации кольца приводят к квадрату, треугольнику, кольцевой шнур даже можно завязать в узел. Все фигуры, показанные на рис. 3.10, топологически эквивалентны. А вот изображенный ранее узел на рис. 3.7 принципиально отличается от того, что показано на рис. 3.10, поскольку его невозможно разложить на столе в виде простой окружности.
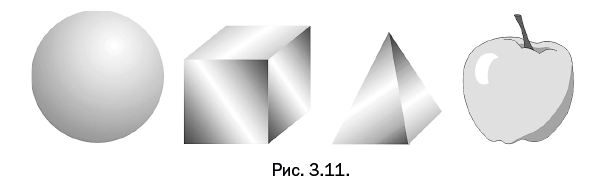
При переходе к объемным телам следует представить себе, что они сделаны из пластилина. Разрешается как угодно деформировать тело, делать в нем вмятины, любые выпуклости. Нельзя лишь проделывать новые сквозные отверстия и залеплять уже имеющиеся. Стало быть, куб, пирамида, цилиндр и яблоко с характерной для него вмятиной и торчащей веточкой тоже топологически эквивалентны (рис. 3.11).
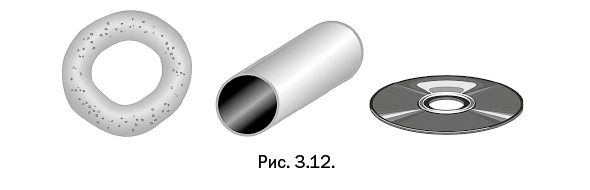
Совсем другую группу образуют тела, имеющие сквозное отверстие. Бублик, труба, компакт-диск образуют топологическое семейство, называемое обобщающим термином «тор» (рис. 3.12).
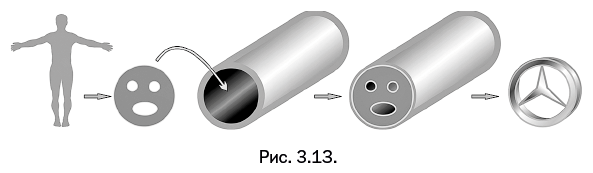
Теперь, используя наши скромные знания топологии, попробуем решить задачу. Что является топологическим эквивалентом тела человека? Не будем принимать во внимание внутреннее пространство организма, где различные органы имеют свои полости. Рассмотрим лишь поверхность тела с учетом тех отверстий, которые выходят наружу. Прежде всего ротовое отверстие, которое, переходя в пищевод и далее в кишечник, заканчивается анальным отверстием. Следовательно, это труба. Мочеиспускательный канал можно не принимать во внимание, поскольку он соединен с замкнутым мочевым пузырем, что аналогично наличию вмятины на поверхности яблока, о чем мы упоминали выше. Эта «вдавленность» не меняет топологических свойств, поэтому ее можно не учитывать. То же самое можно сказать об ушных каналах. А вот ноздри необходимо учесть, так как они соединены с ротовой полостью. Снабдим упомянутую трубу с одного конца заглушкой с тремя отверстиями, которыми будут рот и две ноздри. Сделаем трубу короче и изменим форму трех отверстий. Получим красивую симметричную фигуру – эмблему автомобильной компании «Мерседес». Несколько неожиданный топологический эквивалент человеческого тела, однако это именно так (рис. 3.13).
Существует бесчисленное множество топологических семейств, некоторые реализованы в форме молекул – например, тело произвольной формы внутри полой сферы. Подобные структуры получены, их называют «птичками в клетке». Кроме того, была синтезирована скрученная лента, имеющая одностороннюю поверхность, – лента Мёбиуса, и ее также синтезировал Саваж.
Вернемся к катенанам. Две структуры, показанные на рис. 3.9, по мнению любого химика, представляют собой абсолютно разные соединения, но, с точки зрения "катенанщиков", это всего лишь два решения одной задачи – синтеза двойного катенана. Первым такую задачу решил Саваж.
Назад: Ион металла все упростил
Дальше: От химии к механике

