Книга: Десять уравнений, которые правят миром. И как их можете использовать вы
Назад: 110
Дальше: 112
111
Сейчас я докажу этот результат более строго. Пусть P{Xi = k} – вероятность того, что человек i имеет k подписчиков. Пусть сначала мы выбираем человека j, а затем человека i из числа тех, на кого j подписан. С помощью теоремы Байеса (уравнение 2) мы можем вычислить вероятность:
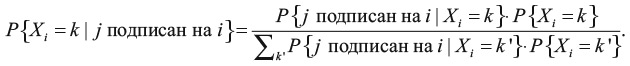
Мы знаем, что P{j подписан на i|Xi = k} = k/N, где N – общее число ребер в графе. Поэтому
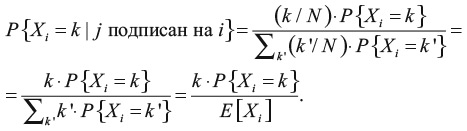
Таким образом, когда k > EXi, то P{Xi = k|j подписан на i} > P{Xi = k}, и наоборот, когда k < EXi, то P{Xi = k|j подписан на i} < P{Xi = k}. Это говорит нам, что случайно выбранный человек, на которого подписан другой случайно выбранный человек, вероятно, имеет больше подписчиков, чем просто случайно выбранный человек.
Чтобы показать, что случайно выбранный человек имеет меньше подписчиков, чем средний человек, на которого он подписан, мы вычисляем ожидаемое (среднее) количество подписчиков для всех людей, на которых подписан j. Оно определяется так:
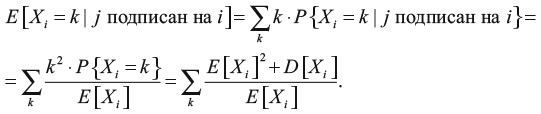
Таким образом:
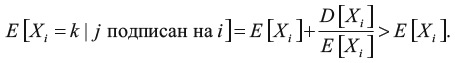
Поскольку E[Xi] = E[Xj] – одно и то же значение для всех людей в социальной группе, ожидаемое количество подписчиков j будет меньше, чем у i (при условии, что j подписан на i).

