Возникает впечатление, что математическая основа некоторых рассмотренных выше алгоритмов оптимизации делает их исключительной прерогативой технологических гигантов, которые массово эксплуатируют эти алгоритмы в коммерческих целях. Однако существуют и более простые алгоритмы – хотя и в их основе лежит сложная математика, – с помощью которых можно вносить вроде бы мелкие, но очень существенные улучшения в нашу повседневную жизнь. Одно из таких семейств известно как «стратегии оптимальной остановки» и позволяет выбрать наилучший момент для вмешательства в процесс принятия решений.

Предположим, например, что вы ищете, куда пригласить своего партнера на ужин. Вы оба очень голодны, но вы бы хотели, чтобы и место было приятным – первое попавшееся не подойдет. Вы считаете, что вполне способны оценить качество каждого ресторана по сравнению с другими. По вашим прикидкам, вы сможете проверить с десяток ресторанов, пока вашему партнеру не надоест шляться туда-сюда. При этом вы не хотите выглядеть нерешительным, поэтому не будете возвращаться в однажды отвергнутый ресторан.

Лучшая стратегия для решения проблем такого рода заключается в том, чтобы посмотреть и сразу отвергнуть некоторые рестораны, чтобы почувствовать общую атмосферу. Вы можете просто выбрать первый ресторан, в который пришли, но, учитывая, что у вас нет абсолютно никакой информации, что это за заведение, есть только один шанс из десяти, что вы случайно выберете лучший. Так что стоит немного подождать и составить мнение о нескольких ресторанах, а потом выбрать первый из тех, что будет лучше, чем все те, в которые вы заходили прежде. Эта стратегия выбора ресторана проиллюстрирована на рис. 21. Первые три ресторана оцениваются, а затем отклоняются. Седьмой ресторан лучше всех предыдущих, поэтому на нем вы и останавливаетесь. Приятного аппетита! Но достаточно ли посетить три ресторана, чтобы получить надежные основания для отказа? Стратегия оптимальной остановки задается вопросом, сколько ресторанов нужно посмотреть и отклонить, чтобы получить представление о том, какой у вас выбор? Если посетите слишком мало ресторанов, вы не поймете, что предлагается к рассмотрению, но если вы исключите из списка слишком много, оставшийся выбор будет ограничен.

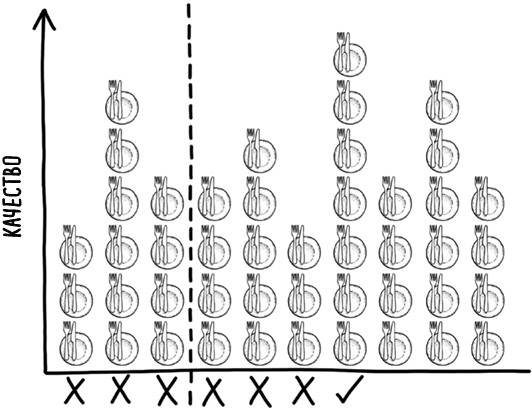
Рис. 21. Оптимальная стратегия заключается в том, чтобы оценить, но отклонить каждый вариант до заданной точки отсечения (пунктирной линии), а затем принять следующий оцениваемый вариант, который лучше всех предыдущих

Математика, стоящая за этой проблемой, сложна, но оказывается, что следует оценить и отвергнуть примерно первые 37 % ресторанов (округленные до трех, если их всего 10), прежде чем выбрать следующий, который лучше всех предыдущих. Точнее, нужно отвергнуть 1/e долю всех доступных вариантов, где e – математическое обозначение числа Эйлера . Число Эйлера составляет приблизительно 2,718, таким образом, 1/e – примерно 0,368 или, в процентном соотношении, 37 %. Рис. 22 иллюстрирует, как меняется вероятность выбора лучшего из 100 ресторанов по мере того, как вы варьируете количество ресторанов, которые отвергаете сразу. Если вы поспешите с решением, оно, по сути, сведется к слепому гаданию, поэтому неудивительно, что при слишком раннем выборе вероятность наткнуться на лучший ресторан низка. Аналогично, если вы выбираете слишком долго, то, скорее всего, вы уже пропустили лучший вариант. Вероятность наилучшего выбора максимальна, когда вы отклоняете первые 37 вариантов.

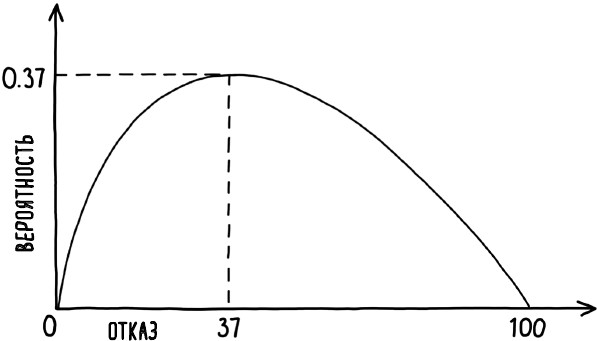
Рис. 22. Вероятность выбора наилучшего варианта максимальна, когда мы оцениваем и отклоняем 37 % вариантов, прежде чем принять следующий, который оценим выше, чем все, что видели прежде. В этом сценарии вероятность выбора лучшего ресторана составляет 0,37, или 37%

Но что, если лучший ресторан был в первых 37 %? В таком случае, вам не повезло. Правило 37 % работает не каждый раз – оно вероятностное. Вообще алгоритм гарантированно работает только в 37 % случаев. Это лучшее, что вы можете сделать в данных обстоятельствах, но это выгоднее, чем 10-процентный шанс на успех, если бы вы выбирали один из 10 ресторанов наугад, и намного выгоднее, чем 1-процентный, если бы вам пришлось выбирать между 100 ресторанами. Чем выше относительная вероятность успеха, тем шире ваш выбор.

Стратегия оптимальной остановки работает не только для ресторанов. На самом деле изначально математики окрестили ее «проблемой найма». Если вы должны по очереди провести собеседование с конечным количеством кандидатов на должность, в конце каждого собеседования сообщив претенденту, получил ли он работу, используйте правило 37 %. Проведите собеседование с 37 % кандидатов и используйте их в качестве ориентира. Возьмите после этого первого кандидата, который окажется лучше всех тех, кого вы видели до него, и откажите остальным.

Когда я подхожу к кассам в моем местном супермаркете, я прохожу мимо первых 37 % (4 из 11), отмечая длину очереди в каждую из них, а затем встаю в первую же очередь, которая короче, чем все остальные, которые я видел. Если я вместе с группой друзей пытаюсь сесть в забитый пассажирами последний поезд после затянувшейся гулянки – да еще так, чтобы мы сели все вместе, мы используем правило 37 %. Мы пробегаем мимо первых трех вагонов состава, который состоит из восьми вагонов, запоминая, сколько в них народу, а затем садимся в первый же вагон, в котором больше свободных мест, чем в любом из первых трех.

Некоторые из этих сценариев несколько надуманны – хотя и навеяны реальным опытом. Но их можно сделать более прагматичными. Что произойдет, если в половине ресторанов, которые вы проверите, не будет свободных мест? В таком случае логично будет сократить время на предварительный отсев ресторанов. Вместо того чтобы проверять первые 37 %, проверьте только первые 25 %, прежде чем выбирать тот, что будет лучше всех остальных, которые вы уже видели.

Или если вы решите, что у вас достаточно времени, чтобы рискнуть – и вернуться к одному из тех вагонов поезда, которые пропустили, но вероятность, что он за это время заполнится, составляет 50 %? Возвращаясь, вы расширяете свои возможности и можете позволить себе искать немного дольше – отказаться от 61 % вагонов впереди перед тем, как выбрать следующий более пустой вагон. Не забывайте, однако, что вам все-таки нужно сесть в поезд прежде, чем он отойдет.

Существуют алгоритмы оптимальной остановки, которые могут подсказать, когда продать свой дом или на каком расстоянии от кинотеатра стоит искать парковку, чтобы шансы найти свободное место были максимальными, а пеший путь до кинотеатра – минимальным. Подвох в том, что чем реалистичнее ситуация, тем сложнее становятся математические выкладки, и простые процентные правила уже не действуют.

Существуют даже алгоритмы оптимальной остановки, которые подскажут, сколько кавалеров (или пассий) вам нужно перебрать, прежде чем задумываться о браке. Сначала нужно решить, сколько увлечений вы захотите пережить к тому времени, когда пожелаете остепениться. Допустим, вы остановитесь на одном романе в год с 18 по 35 лет, что составит в общей сложности 17 потенциальных партнеров на выбор. Стратегия оптимальной остановки предполагает, что вы играете на этом поле около шести или семи лет (примерно 37 % от 17 лет), определяясь с выбором. После этого вы должны остаться с первым же человеком, который вам подойдет лучше всех тех, с кем вы встречались до того.

Идея подчинить свою романтическую жизнь заданному набору правил придется по душе немногим. Что, если в первых 37 % вы найдете того, с кем по-настоящему счастливы? Можете ли вы действительно хладнокровно отвергнуть свои чувства, следуя любовной миссии по алгоритму? Что, если человек, которого алгоритм определил вам в спутники жизни, вовсе не считает вас наилучшей парой для себя? Что, если ваши приоритеты изменятся на полдороге? К счастью, в сердечных вопросах, как и в других, более очевидных математических проблемах оптимизации, нам не всегда нужно искать лучшее решение, тот единственный и неповторимый Идеал. Скорее всего, есть несколько человек, которые будут вам хорошей парой и с которыми вы сможете быть счастливы. Оптимальная остановка не дает ответов на все вопросы в жизни.

Вообще, при всех потрясающих способностях облегчать многие аспекты нашей повседневности, алгоритмы подходят для решения далеко не всякой задачи. Алгоритмы можно использовать для упрощения и ускорения монотонной задачи, но полагаться на них постоянно – слишком рискованно. Их триединая природа – ввод данных, свод правил и вывод данных – означает, что есть три области, где может произойти сбой. Даже если пользователь уверен, что правила процедуры определены в соответствии с его требованиями, неосмотрительный ввод данных и бесконтрольный их вывод могут привести к катастрофическим последствиям, как убедился на собственном горьком опыте онлайн-продавец Майкл Фаулер. Вдохновленный алгоритмами гениальный план американского торговца, обернувшийся неожиданным крахом в 2013 году, уходит корнями в историю Британии начала Второй мировой войны.