Экспоненциальный рост – это возрастание любой величины пропорционально ее текущим размерам. Представьте, что утром, когда вы открываете пакет молока, туда, прежде чем снова наденете крышку, проникает одна клетка Streptococcus faecalis – бактерии стрептококка группы D. Стрептококк группы D – одна из бактерий, вызывающих скисание и свертывание молока, но разве единственная клетка – повод для беспокойства? Возможно, вас насторожит способность клетки стрептококка группы D делиться в молоке, производя две дочерние клетки каждый час . С каждым новым поколением число клеток увеличивается пропорционально текущему их числу, поэтому общее количество стрептококка растет в геометрической прогрессии.

Кривая, описывающая экспоненциальный рост, напоминает любимую роллерами, скейтбордистами и велосипедистами-трюкачами рампу в четверть трубы. Первоначально градиент рампы очень низкий – кривая очень пологая и набирает высоту лишь постепенно (что и демонстрирует первая линия на рис. 2).

Через два часа в вашем молоке резвятся уже 4 клетки стрептококка, а через четыре часа – 16. Пока что это не выглядит чем-то ужасным, так? Но, как и у рампы, высота экспоненциальной кривой и ее крутизна быстро растут. Рост в геометрической прогрессии поначалу представляется медленным, поэтому последующий резкий взлет может показаться неожиданным. Если оставить молоко на 48 часов, и экспоненциальный рост клеток стрептококка продолжится, то когда вы решите снова попить молока, в пакете может оказаться почти квадриллион (1 000 000 000 000 000) клеток – достаточно, чтобы свернулась ваша кровь, не говоря уж о молоке. В этот момент клеток будет больше, чем людей на нашей планете – 130 000 к одному. Экспоненциальные кривые иногда называют J-образными, так как они почти повторяют крутую кривую буквы J. Разумеется, по мере того, как бактерии используют питательные вещества в молоке и меняют его кислотность (рН), условия для роста ухудшаются, а его экспоненциальность сохраняется относительно недолго. На деле почти в каждом реальном сценарии долгосрочный экспоненциальный рост оказывается неустойчивым, а во многих случаях и патологическим, поскольку растущий объект истощает ресурсы донора, лишая его жизнеспособности. Так, устойчивый экспоненциальный рост клеток в организме является характерным признаком рака.

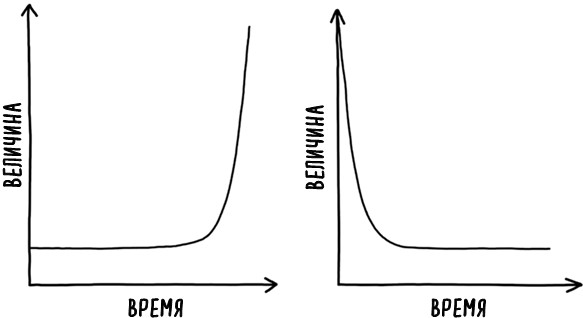
Рис. 2. J-образная кривая экспоненциального роста (слева) и спада (справа)

Другой пример экспоненциальной кривой – водная горка с эффектом свободного падения: в своей верхней части она настолько крута, что посетители этого аттракциона испытывают чувство невесомости. Спускаясь по такой горке, мы путешествуем по экспоненциальной кривой спада, а не по кривой роста (пример такого графика – вторая линия на рис. 2). Экспоненциальное затухание происходит, когда количество уменьшается пропорционально своему текущему объему. Представьте, что вы открываете огромный пакет М&Ms, выливаете их на стол и съедаете все конфетки, упавшие на стол буквой М кверху. Остальное кладете обратно в пакет – до завтра. На следующий день встряхните пакет и снова вывалите конфеты на стол. Снова съешьте все те, что лежат буквой M кверху, а остальное положите обратно. Каждый раз, когда вы выливаете конфеты из пакета, вы съедаете примерно половину от остатка, независимо от того, сколько конфет вы съели в первый раз. Количество конфет уменьшается пропорционально количеству оставшихся в пакете, то есть происходит экспоненциальное падение их общего числа. Точно так же экспоненциальная водяная горка начинается высоко и почти вертикально, так что скатывающийся падает очень быстро. Когда у нас много конфет, то и на съедение их выпадает много. Но кривая постепенно теряет свою крутизну, пока не станет почти горизонтальной к концу горки; чем меньше сладостей у нас остается, тем меньше конфет мы получаем с каждым новым днем. Каждая конкретная конфета падает буквой М вверх или вниз случайно и непредсказуемо, но предсказуемое затухание экспоненциальной кривой водной горки проявляется в количестве остающихся у нас с течением времени конфет.

В этой главе мы выявим скрытую связь между экспоненциальным поведением и повседневными явлениями: распространением эпидемии в популяции или мемов в интернете; быстрым ростом эмбриона и слишком медленным ростом денег на наших счетах; тем, как мы воспринимаем время, и даже тем, как взрывается ядерная бомба. По ходу дела мы постепенно и аккуратно раскроем всю трагедию пирамиды «Отдай и получи». Истории людей, потерявших сбережения в подобных схемах, демонстрируют, как важно уметь мыслить экспоненциально, что, в свою очередь, поможет нам предвосхищать невероятные порой темпы изменений в современном мире.