ПРИМЕЧАНИЯ
ЧАСТЬ I. ДУМАТЬ КАК МАТЕМАТИК
. Происхождение этой игры теряется в тумане. Возможно, впервые ее правила были изложены в журнале Games в конце 1990-х или начале 2000-х (хотя на мой запрос сотрудники редакции ответили, что никогда не слышали об этой игре). В 2009-м версия под названием «Тик-так-ку» (с фишками на деревянной доске) завоевала премию Менсы за лучшую американскую настольную игру. Возможно, эту игру независимо придумывали несколько раз, как некоторые танцы или дифференциальное исчисление.
. Когда я впервые продемонстрировал эту игру моим ученикам в Оклендской чартерной средней школе (Oakland Charter High School) в 2012 году, они-то и окрестили ее «жесткие крестики-нолики» (Ultimate Tic-Tac-Toe). Мой пост в блоге с таким заголовком вызвал всплеск популярности: статью в «Википедии», несколько научных статей и множество мобильных приложений. Мораль: гордитесь, матадоры! Вы придумали название для этой штуковины.
. Я благодарен Марку Торнтону, который прочел черновик этой главы и задал в точности тот же самый вопрос. Правки Майка сродни текстам песен Леонарда Коэна или прозе Хемингуэя: я всегда знал, что они хороши, но чем старше я становлюсь, тем больше ценю их.
. Ключевая идея заключается в том, что у продолговатых прямоугольников непропорционально большой периметр, а у похожих на квадраты — непропорционально большая площадь. Поэтому нужно просто взять продолговатый прямоугольник (например, 10×1) и почти квадратный (например, 3×4).
. Если в ответе должны быть целые числа, задача становится еще веселее. Вот мой вывод формулы, порождающей целое семейство решений:

Решений бесконечно много, но некоторые все равно остаются вне поля зрения, потому что другие значения d тоже могут давать целочисленные значения c. Например, эта формула не дает моего любимого решения: 1 × 33 и 11 × 6. Мой коллега Тим Кросс, съевший собаку на диофантовых уравнениях, подсказал мне ловкий способ найти все целочисленные решения. Моей профессии свойственна мизантропия, поэтому на сей раз я предлагаю читателю найти этот способ самостоятельно.
. Эта стратегия слишком сложна, чтобы полностью изложить ее здесь, но она реализована коллегами из Академии Хана: .
. Я рекомендую прочесть эту историю целиком: Simon Singh, Fermat’s Last Theorem (London: Fourth Estate Limited, 1997). [Сингх C. Великая теорема Ферма. — М.: МЦНМО, 2000.]
. Цитата из единственного словаря, чтение которого доставляет мне удовольствие: David Wells, The Penguin Book of Curious and Interesting Mathematics. — London: Penguin Books, 1997.]
. По правде говоря, я скорее уж фанат «Голодных игр».
. Майкл Першен, удивительный человек и обладатель самого аналитического интеллекта на свете, сформулировал идеи этих «стратегий» раньше, чем они пришли мне в голову. Я благодарю его за помощь при написании этой главы.
. Посмотрите милый мультфильм на эту тему: .
. Моя жена математик; мы в браке уже пять лет, но, кажется, она по-прежнему помнит, как меня зовут.
. Подробнее: Matthey Parker, Things to Make and Do in the Fourth Dimension. — London: Penguin Random House, 2014. [Паркер М. Чем заняться в четвертом измерении? — М.: АСТ, 2020.]
. Я благодарен Мэтью Фрэнсису и Эндрю Стейси за помощь по этому вопросу. Я хотел написать, что Вселенная «гиперболическая» или «эллиптическая», а не «евклидова», но они сообщили мне, что в действительности она представляет собой труднопостигаемое лоскутное одеяло из этих более простых геометрий.
Стейси написал: «Риманова геометрия обобщает евклидову во многих отношениях; она намного богаче евклидовой, но упускает из виду некоторые аспекты, в первую очередь то, как объекты соотносятся друг с другом в различных областях пространства». Это включает и понятие параллельных прямых.
Фрэнсис добавил интересную историческую деталь: «В XIX веке Уильям Кингдон Клиффорд предложил использовать неевклидову геометрию, чтобы заменить физическое понятие силы, но он просто полагал, что “это было бы прикольно”. Меня не удивило бы, если другие тоже продумывали подобные идеи». Естественно, Эйнштейн тесно сотрудничал с математиками; ни один прорыв не происходит сам по себе.
. Эта история изложена в графическом романе: Apostolos Doxiadis et al., Logicomix: An Epic Search for Truth (New York: Bloomsbury, 2009). [Доксиадис А., Пападимитриу Х. Логикомикс. Поиск истины. — М.: Карьера Пресс, 2019.]
. James Gleick, The Information: A History, a Theory, a Flood (New York: Knopf Doubleday, 2011). Блестящая книга. [Глейк Дж. Информация. История. Теория. Поток. — М.: Corpus, 2013.]
. Eugene Wigner, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Richard Courant lecture in mathematical sciences delivered at New York University, May 11, 1959”, Communications on Pure and Applied Mathematics 13 (1960): 1–14. Сногсшибательное эссе. [Статья Юджина Вигнера «Непостижимая эффективность математики в естественных науках» в переводе В. А. Белоконя и В. А. Угарова была опубликована в журнале «Успехи физических наук» в 1968 году (Т. 94, С. 535–546; ). — Прим. науч. ред.]
. Моим учителем в этой главе был Дэвид Кламп, чьи замечания сочетали эрудицию кого-то вроде Карла Сагана с мягкой человечностью кого-то вроде Карла Сагана (похоже, Дэвид и есть Карл Саган).
. Israel Kleiner, “Emmy Noether and the Advent of Abstract Algebra,” A History of Abstract Algebra (Boston: Birkhäuser, 2007), 91–102, . Я исказил аргумент Клейнера; ключевая идея в том, что в XIX веке удалось добиться больших успехов в геометрии и математическом анализе, но алгебра оставалась в первозданном закостенелом состоянии.
. Joaquin Navarro, Women in Maths: From Hypatia to Emmy Noether. Everything is Mathematical (Spain: R. B. A. Coleccionables, S. A., 2013) [Наварро Х. Женщины-математики: от Гипатии до Эмми Нётер. Вып. 37. 2014. — (Сер.: Мир математики).]
. Профессор Грейс Шоуэр Квин. См.: Marlow Anderson, Victor Katz, and Robin Wilson, Who Gave You the Epsilon? And Other Tales of Mathematical History (Washington, DC: Mathematical Association of America, 2009).
. См. интервью с Сильвией Серфати: Siobhan Roberts, “In Mathematics, ‘You Cannot Be Lied To,’” Quanta Magazine, February 21, 2017, . Я рекомендую статьи Робертса о математике так же горячо, как альбомы R. E. D.
. Colin McLarty, “The Rising Sea: Grothendieck on Simplicity and Generality,” May 24, 2003, .
. Natalie Wolchover, “A Long-Sought Proof, Found and Almost Lost,” Quanta Magazine, March 28, 2017, . Это грандиозная статья. Надеюсь, вы простите меня за спойлеры.
. Фарад Райахи (1939–2011).
. Тогда как имя Кори было псевдонимом, эту девочку по-настоящему звали Вианни. Я думаю, она заслуживает славы. Я воспроизвожу диалог по памяти, но в общем и целом все так и было.
. Использованы цитаты из выступления Тяу на пресс-конференции на Гейдельбергском форуме лауреатов в 2016 году. Я от всего сердца благодарю первоклассного человека Уайлдера Грина и команду HLF за возможность побывать на этом форуме.
ЧАСТЬ II. ДИЗАЙН. ФУНКЦИОНАЛЬНАЯ ГЕОМЕТРИЯ
. Углы правильного пятиугольника равны 108°. Если начертить три пятиугольника с общей вершиной, останется зазор в 36° до развернутого угла и не останется места для четвертого пятиугольника. Из всех правильных многоугольников можно замостить плоскость только треугольниками (60°), квадратами (90°) и шестиугольниками (120°), поскольку все эти числа — делители 360°.
. Некоторая гибкость все же имеет место. Я уже приводил в качестве примера постулат Евклида о параллельных прямых; вы можете выбрать другой постулат. Но когда вы возьмете его за основу, все теоремы будут вытекать из него с логической необходимостью.
Почему я низвел столь важное возражение в незаметную сноску? Ну, я полагаю, если вы достаточно дотошны, чтобы усомниться, что мы живем в евклидовом пространстве, то въедливо проинспектируете все сноски.
. Необходимо отметить основной источник этой главы: Mario Salvadori, Why Buildings Stand Up (New York: W. W. Norton, 1980). Великолепная, внятная книга, без которой эта глава была бы шаткой, как ошибочное доказательство. Кроме того, я благодарен за помощь при написании этой главы Уиллу Уонгу, архитектору мысли и победителю университетских спортивных турниров.
. Я узнал о египетских вязальщиках узлов из книги: Kitty Ferguson, Pythagoras: His Lives and the Legacy of a Rational Universe (London: Icon Books, 2010).
. Усеченная пирамида — многогранник с двумя параллельными основаниями и гранями-трапециями. По-английски она называется frustum — это слово стоит знать.

. «Википедия» указывает размеры трех туннелей (нисходящего, восходящего и горизонтального) и трех камер (Царская палата, Царицына палата, большая галерея). Их суммарный объем составляет около 1340 м3, т.е. примерно 0,05% от объема пирамиды 2 600 000 м3. Я округлил это число до 0,1%, затем (снова низкий поклон «Википедии») вычислил объем Эмпайр-стейт-билдинг (2 800 000 м3), и 0,1% от этого числа составляет 2800 м3. Разделив объем на площадь одного этажа (около 7400 м2), вы получите высоту 38 см. Но едва я закончил рукопись книги, в пирамиде была обнаружена потайная камера! Я округлил до двух футов (около 60 см), и мое округление покрывало эту неучтенную ошибку.
. Каламбур, сознательный на 100%.
. Я умыкнул эти сведения из книги Сальвадори (Why Buildings Stand Up) и, вне всяких сомнений, что-нибудь упустил в пересказе.
. Я снова позаимствовал эту информацию у Сальвадори. Как отмечает Уилл Уонг, в более традиционном представлении на первый план в этом случае выходят нужные нам свойства (распределение напряжение, предотвращение крутящего момента и т.д.), обусловленные тем, что поперечное сечение балки имеет форму буквы I.
. Мои познания о ферменных конструкциях почерпнуты из величайшего человеческого творения — «Википедии». Подробности на страницах и .
. Благодарю Кэролайн Гиллоу и Джеймса Батлера (чьи души настолько велики, что разделяющий нас Атлантический океан выглядит просто лужицей) за помощь и поддержку при написании этой главы и за то, что опыт пребывания в Англии был настолько замечательным.
. В тот же день мой 11-летний ученик Гарри на мою приветственную реплику: «Ну, как ваш синус-косинус?» — откликнулся: «Сикось-накось!» Я же говорил, преподавать — это кайф.
. Я зашел чересчур далеко, ревностно защищая формат бумаги А4. Возможно, потому-то меня и прозвали «неистовый Орлин». (NB: пожалуйста, никогда не называйте меня «неистовый Орлин».) Я сказал, что формат бумаги 8,5 на 11 дюймов никак не соотносится с другими форматами, но это клевета. Удвоение листа дает формат побольше (11 на 17 дюймов), располовинивание листа дает формат поменьше (5,5 на 8,5 дюймов). В этом смысле наш формат ничем не хуже A4.
Но есть одна загвоздка. В формате 8,5 на 11 дюймов одна сторона длиннее другой в 1,29 раз; в соседних форматах это соотношение составляет 1,55. Короче говоря, они имеют разную форму. Если вы когда-нибудь пытались уменьшить или увеличить масштаб ксерокопии, вы понимаете, какую головную боль вызывает это обстоятельство.
Так чем же уникальна серия форматов A1, А2 и так далее? Своей пропорциональностью. Листы бумаги в этой славной череде представляют собой подобные друг другу прямоугольники, отмасштабированные версии своих собратьев.
Я все это знал, когда работал над главой, но все же слишком далеко зашел в пылу риторики. Я благодарю Джо Суини за эту поправку и приношу свои извинения формату 8,5 на 11 дюймов: конечно, он по-прежнему неполноценен, но все же не настолько плох, как я предполагал.
. Еще одна отрада в том, что площадь любого листа А1 в точности равна 1 м2, и лист очередного формата вдвое меньше предыдущего по площади. Таким образом, восемь листов А4 имеют общую площадь в точности 1 м2 (хотя нет, не в точности… из-за иррациональности).
. Когда я работал над этой главой, мой коллега и образец для подражания Ричард Бриджес указал мне на прекрасное изложение тех же идей в эссе 90-летней давности. Я многое позаимствовал оттуда: J. B. S. Haldane, “On Being the Right Size,” март 1926, .
. Я пренебрегаю высотой, потому что при готовке шоколадных тортов вы никогда не заполняете форму тестом доверху.
. Я узнал эту историю из книги Kitty Ferguson, Pythagoras: His Lives and the Legacy of a Rational Universe (London: Icon Books, 2010). Как и многие басни, она, скорее всего, носит апокрифический характер.
. Джон Коуэн (я благодарю его за сверку фактов в этой главе и за то, что он никогда не кичится и не подавляет своей эрудированностью) добавил один штрих: «На самом деле Колосс Родосский, как и статуя Свободы, был полым: бронзовые пластины и железные арматурные прутья. Следовательно, при увеличении высоты в n раз цена вырастала всего лишь в n2 раз». Все равно чересчур для бедняги Хареса.
. Впервые я узнал об этом в колледже из курса Лори Сантос «Секс, эволюция и человеческая природа». Нет, я, конечно, уже знал, что великанов не существует, но объяснения профессора Сантос (возможно, как я сейчас вижу, вдохновленные Холдейном) помогли сформировать костяк этой главы.
. Пожалуйста, дозвонитесь до ваших сенаторов и убедите их профинансировать жизненно важные объекты инфраструктуры Дуэйна Джонсона, пока не стало слишком поздно.
. Математика сопротивления воздуха лежит в основе еще одной короткой басни: «Зачем большим кораблям огромные паруса». Когда вы удваиваете размеры вашего корабля, его площадь (2D) учетверяется, но масса (3D) увеличивается в восемь раз. Вы будете ловить относительно меньше ветра, если не измените пропорции. Поэтому, если корабль в два раза длиннее, его мачты примерно в три раза выше.
. Джон Коуэн добавляет: «Еще одна особенность муравьев — у них нет кровеносной системы, потому что они настолько малы, что не требуется внутренняя жидкость, чтобы распространять по телу кислород». Для существ, у которых меньше объема на единицу площади, достаточно диффузии.
. См. . Эта виньетка черпает вдохновение из блога учителя математики под ником The Chalk Face [Лицо, испачканное мелом].
. Вот еще несколько историй, не уместившихся в этой главе:
1. Почему большие воздушные шары более рентабельны? Потому что цена материала зависит от площади поверхности (2D), а подъемная сила от объема гелия (3D).
2. Почему огромных диноптиц, например индеек, приходится так долго держать в духовке? Потому что количество поглощаемого тепла растет при увеличении площади поверхности (2D), но требуется тем больше тепла, чем больше объем (3D).
3. Почему сухая пшеница совершенно безопасна, а пшеничная мука взрывоопасна? Потому что экзотермические химические реакции происходят на поверхности вещества, и крохотные частицы пыли имеют куда большую суммарную площадь поверхности на единицу объема площади, чем цельные колосья пшеницы.
. Впервые я узнал о парадоксе Ольберса от Питера ван Доккума, который вел курс, посвященный галактикам и космологии. Если вас восторгает (или раздражает) эклектизм этой главы, то причина только в том, что я получил образование по системе свободных искусств и наук (Liberal Arts).
. Я уступлю последнее слово Джону Коуэну: «Что, если между нами и звездами есть какие-нибудь Темные Вещи (планеты, пыль и т.д.)? Не станут ли некоторые звезды из-за этого невидимыми, не исчезнет ли парадокс? Нет, потому что звезды, заслоненные Темными Вещами, со временем разогрели бы их до звездной температуры, упразднив всю темноту».
. E. A. Poe, Eureka: A Prose Poem (New York: G. P. Putnam, 1848). [По Э. Эврика. Поэма в прозе (Опыт о вещественной и духовной Вселенной). Пер. К. А. Бальмонта. — М.: Эксмо,2008.]
. Исторические факты, приведенные в этой главе, я почерпнул из трех источников. Перечисляю их по убыванию объема позаимствованной информации:
- Deborah J. Bennett, Randomness (Cambridge, MA: Harvard University Press, 1998).
- “Rollin’ Bones: The History of Dice,” Neatorama, August 18, 2014. Из книги Uncle John’s Unsinkable Bathroom Reader, .
- Martin Gardner, “Dice,” in Mathematical Magic Show (Washington, DC: Mathematical Association of America, 1989), 251–62.
. У курносого дисфеноида есть два кузена: грани этих полиэдров — равносторонние треугольники, но одни грани все равно будут выпадать чаще, чем другие: (1) трижды наращенная треугольная призма (спасибо за подсказку Лоуренсу Рэкхему) и (2) скрученно удлиненная четырехугольная бипирамида (спасибо за подсказку Тиму Кроссу и Питеру Оллису). Если вы предпочитаете четырехугольные грани, есть и (3) псевдодельтоидальный икоситетраэдр (спасибо за подсказку Александру Мюницу).
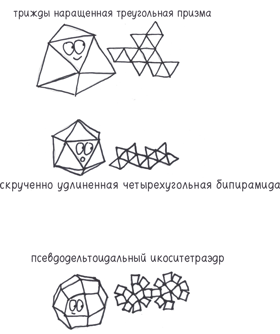
. Честно говоря, прецеденты имеются. Древние жители долины реки Инд использовали треугольные продолговатые игральные кости, слепленные из глины. Их современники в Индии использовали прямоугольные параллелепипеды, выточенные из слоновой кости.
. Возможно, это обстоятельство объясняет, почему все современные продолговатые игральные кости, которые мне довелось увидеть, или (1) крошечные, или (2) перекручены так, чтобы длинные грани оставались эквивалентными, обеспечивая удовлетворительное, сдержанное кувыркание. The Dice Lab (Лаборатория игральных костей), чья работа помогла мне найти вдохновение для этой главы, продает несколько симпатичных экземпляров второго вида.
. Подробнее этот аргумент изложен здесь: Persi Diaconis and Joseph B. Keller, “Fair Dice,” American Mathematical Monthly 96, no. 4 (April 1989): 337–39. .
. Тем не менее некоторые цивилизации предпочитали этот способ. Древние инуиты кидали игральные кости в виде стульев, учитывая только три грани из шести. Индейцы папаго кидали кости бизонов, учитывая только две из четырех сторон.
. Гениальные и зловредные подробности здесь: John Scarne, Scarne on Dice, 8th ed. (Chatsworth, CA: Wilshire Book Company, 1992).
. Похожий метод, далекий от учтивости, но элегантный, использовал гангстер Большой Джул в мюзикле «Парни и куколки». На его игральных костях вообще не было точек. Но не волнуйтесь: Большой Джул прекрасно помнил, сколько точек было на какой грани.
. Ну… почти. Настоящий знаток может распознать обман, потому что с определенного ракурса будет видно, что разметка граней необычная, как будто ее отразили в зеркале. По этой и другим причинам мошенники никогда не позволяют игральным костям долго оставаться в поле зрения, чтобы не попасться.
. Ральф Моррисон, знаток всего обычного и необычного, рассказал мне, что Лаборатория игральных костей продает умопомрачительные 120-гранные игральные кости. Подробнее: Siobhan Roberts, “The Dice You Never Knew You Needed,” Elements, New Yorker, April 26, 2016, .
. На самом деле я почерпнул многое из книги: Ryder Windham, Chris Reiff, and Chris Trevas, Death Star Owner’s Technical Manual (London: Haynes, 2013). Я написал эту главу отчасти для того, чтобы вызвать улыбку Нейла Шепарда, но не передавайте ему мои слова.
. Если вы интересуетесь такого рода вещами, я рекомендую: Trent Moore, “Death Star Architect Defends Exhaust Ports in Hilarious Star Wars ‘Open Letter,’” SyFy Wire, February 14, 2014, .
. Благодарю Грегора Назариана, который смягчил мое сердце, как музыкальная тема Джона Уильямса, и помог существенно улучшить эту главу. (Я упоминаю его здесь, потому что он подсказал мне идею с дианогой, а не потому, что его лицо напоминает дианогу.)
. Информация о ледяных и каменных шарах почерпнута от Меган Вивелл из Национального Космического центра, источник: Jonathan O’Callaghan, “What Is the Minimum Size a Celestial Body Can Become a Sphere?” Space Answers, October 20, 2012, . Плотность имперской стали — моя экстраполяция.
. Мои расчеты дают результат от 120 до 150 км.
. Я снова и снова проводил изыскания, пытаясь обнаружить более реалистичные данные, но все источники, похоже, близко сходятся в этом вопросе. Фанаты «Звездных войн» дискутировали по этому вопросу и пришли к оценке от одного до двух миллионов: . Уайндэм и другие дают грубую оценку 1,2 млн человек и 400 000 дроидов. «Википедия» пишет про 1,7 млн человек и 400 000 дроидов. Чтобы доказать устойчивость моей позиции, я взял самую высокую оценку из обнаруженных.
. Я не уверен, что успешно вплел это повествование в канву событий с учетом нового фильма «Изгой-один». Вне всяких сомнений, вольности, которые я себе позволил, огорчат по-настоящему непреклонных и достойных восхищения блюстителей канона. С другой стороны, я дал этим персонажам доступ к данным переписи в Западной Вирджинии за 2010 год, поэтому, возможно, перераспределение конструкторских заслуг — еще не худшее мое прегрешение. [Вероятно, самая большая вольность — воскрешение гранд-моффа Таркина ради этого интервью. В фильме он погиб вместе со «Звездой смерти». — Прим. пер.]
ЧАСТЬ III. ВЕРОЯТНОСТЬ. «МОЖЕТ БЫТЬ» В МАТЕМАТИКЕ
. Zac Auter, “About Half of Americans Play State Lotteries,” Gallup News, July 22, 2016, . Однако по-прежнему верно, что лотерея — своего рода «регрессивный налог», потому что, если бедный человек тратит ту же сумму денег, что богатый, она составляет больший процент его дохода.
. DiFiore, “15 States Where People Spend the Most on Lotto Tickets,” Credit.com, July 13, 2017, . Хотя статистика меняется из года в год, Массачусетс остается среди лидеров по этому показателю с 1987 года (между прочим, это год моего рождения).
. Информация с сайта MassLottery.com: .
. Попробуем. «Приз 10 000 тортилий», «Приз 10 000 рукопожатий», «Приз 10 000 обнимашек с щенками». Да, это беспроигрышный зачин.
. Примерно половина из них просто вернула вам потраченный доллар, поэтому, возможно, стоит сказать не «выигрышные», а «непроигрышные».
. Charles Clotfelter and Philip Cook, “On the Economics of State Lotteries,” Journal of Economic Perspectives 4, no. 4 (Autumn 1990): 105–19, .
. Kent Grote and Victor Matheson, “The Economics of Lotteries: A Survey of the Literature,” College of the Holy Cross, Department of Economics Faculty Research Series, Paper No. 11-09, August 2011, . Пользуясь случаем, я хочу выразить огромную признательность Виктору Мэтисону, за то что он нашел время посмотреть черновик этой главы.
. Alex Bellos, “There’s Never Been a Better Day to Play the Lottery, Mathematically Speaking”, Guardian, January 9, 2016, .
. Victor Matheson, Kent Grote, “In Search of a Fair Bet in the Lottery,” College of the Holy Cross Economics Department Working Papers. Paper 105, 2004, .
. Например, синдикат Стефана Клинцевича купил 80% билетов Национальной лотереи Ирландии в 1992 году. Его команда вынуждена была разделить главный приз с другими игроками, но извлекла прибыль благодаря тому, что выиграла большинство второстепенных призов. Клинцевич сказал журналистам, что избегает Национальной лотереи Великобритании, потому что там слишком мало этих второстепенных призов. Источник: Rebecca Fowler, “How to Make a Killing on the Lottery,” Independent, January 4, 1996, .
. Впервые я прочел эту историю в одной из самых свежих научно-популярных книг по математике: Jordan Ellenberg, How Not to Be Wrong (New York: Penguin Books, 2014). [Элленберг Дж. Сила математического мышления. — М.: МИФ, 2017.] Затем я проследил, как развивался этот сюжет, по трем восхитительным старым газетным заметкам: (1) “Group Invests $5 Million to Hedge Bets in Lottery”, New York Times, February 25, 1992, ; (2) “Group’s Lottery Payout is Postponed in Virginia”, New York Times, March 7, 1992, ; (3) John F. Harris, “Australians Luck Out in Va. Lottery”, Washington Post, March 10, 1992, .
. Anne L. Murphy, “Lotteries in the 1690s: Investment or Gamble?” University of Leicester, dissertation research, . Мне нравятся названия лотерей в Англии XVII столетия, например «Честное предложение» или «Почетное предприятие». С тем же успехом они могли быть названы «Да, мы знаем, что можем околпачить вас, но обещаем этого не делать».
. Если вы из тех, кто читает примечания, то вы наверняка знаете, о чем речь, но я все же сошлюсь: Daniel Kahneman, Thinking Fast and Slow (New York: Farrar, Straus and Giroux, 2011). [Канеман Д. Думай медленно… Решай быстро. — М.: АСТ, 2014.]
. Daniel Kahneman, Amos Tversky, “Prospect Theory: An Analysis of Decision Under Risk,” Econometrica 47, no. 2 (1979): 263, .
. Charles T. Clotfelter and Philip J. Cook, “On the Economics of State Lotteries,” Journal of Economic Perspectives 4(4), 105–119.
. Derek Thompson, “Lotteries: America’s $70 Billion Shame,” Atlantic, May 11, 2015, . Смотрите также: Mona Chalabi, “What Percentage of State Lottery Money Goes to the State?” FiveThirtyEight, November 10, 2014, .
. Еще в 1790-х годах французские революционеры считали лотерею злым излишеством монархического государства. Но они не решались отменить ее после захвата власти по той простой причине, что нуждались в деньгах. Как иначе превратить налогофобов в добросовестных налогоплательщиков? Источник: Gerald Willmann, “The History of Lotteries,” Department of Economics, Stanford University, August 3, 1999, .
. Charles T. Clotfelter and Philip J. Cook, “On the Economics of State Lotteries,” Journal of Economic Perspectives 4(4), 105–119.
. Gerald Willmann, “The History of Lotteries”.
. В среднем в призовой фонд «Бинго» уходит 74 цента с каждого доллара. На скачках — 81 цент. В игровых автоматах — 89. В государственных лотереях — 50 центов. Источник: Charles T. Clotfelter and Philip J. Cook, “On the Economics of State Lotteries,” Journal of Economic Perspectives 4(4), 105–119.
. Джеральд Уиллманн.
. Kent Grote and Victor Matheson, “The Economics of Lotteries”.
. The Lottery: Last Week Tonight with John Oliver (HBO), HBO, опубликовано на YouTube 9 ноября 2014 года, .
. Почему люди среднего возраста тратят нешуточные суммы на лотерейные билеты? Не берусь утверждать наверняка, но, возможно, потому, что средний возраст — лучшее время для того, чтобы предаваться грезам о выигрыше в лотерею. Молодые люди способны увидеть иные пути попытать счастья. Люди постарше не настолько страстны. Лишь люди средних лет уже достаточно стары, что осознать, что особого волшебства на финансовой почве не предвидится, но еще достаточно молоды, чтоб его возжелать.
. Полностью дискуссию на основе актуальных данных см.: Bourree Lam, “What Becomes of Lottery Winners?” Atlantic, January 12, 2016, .
. Например: Milton Friedman and L. J. Savage, “The Utility Analysis of Choices Involving Risk,” Journal of Political Economy 56, no. 4 (August 1948): 279–304, .
. Kent Grote and Victor Matheson, “The Economics of Lotteries”.
. My example is adapted from Clotfelter and Cook.
. Типичная сценка в апреле 2010 года:
КИЗА (ее глаза лучатся любопытством). Что именно происходит в эндоплазматическом ретикулуме?
Я. Нет ни единого шанса узнать. Это неразрешимая загадка, за пределами человеческого воображения.
ТИМ (монотонным скучающим голосом). В учебнике написано, что там сворачиваются белки.
Я. Ну разумеется, Тим. Я имел в виду — помимо этого.
. Статья, гораздо более заумная, чем моя глава, но все еще читабельная: Razib Khan, “Why Siblings Differ Differently,” Gene Expression, Discover, February 3, 2011, .
. Та же логика лежит в основе концепции энтропии, тенденции Вселенной к беспорядку.
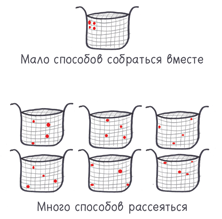
Вообразите множество кирпичей. Есть крайне мало способов построить из них здание и много тоскливых, однообразных способов свалить их в кучу или разбить на осколки. Со временем случайные изменения накапливаются; есть почти нулевая вероятность, что кирпичи сами собой образуют здание; скорее всего, они всё больше будут рассыпаться. Таким образом, время предпочитает осколки, а не кирпичи.
Точно так же у частиц пищевого красителя есть крайне мало способов собраться всем вместе с одной стороны стакана воды; все молекулы тогда как будто перекувыркнутся через голову. Но у этих частиц есть много-много способов более или менее равномерно распределиться внутри жидкости; каждое распределение будет похоже на уникальную комбинацию орлов и решек. Именно поэтому случайные процессы сумасбродно и неумолимо ведут к увеличению энтропии, равномерному смешению составных частей Вселенной. Космическое предпочтение беспорядка по сути своей комбинаторно.
. Вероятность этого варианта — около 96%, поэтому в одном случае из 25 мое пророчество не сбудется. Однако если хотя бы 25 читателей действительно подбросят 46 монет, то аудитория научно-популярных книг по математике еще более упертая, чем я подозревал.
. Я получил этот график непосредственно от Блейна. См. подробности по ссылке: .
Ось абсцисс обозначена «сантиморганы» — один из самых запутанных научных терминов (во всяком случае, для меня). Сантиморган — это длина хромосомы, которая с вероятностью 1% распадется в результате рекомбинации хромосом в любом из данных поколений. У вас очень много общих черт с близкими родственниками и очень мало — с дальними. Таким образом, общие сантиморганы — это показатель генетической близости.
Пока что все ясно. Но из-за того, что кроссинговер происходит с разными вероятностями по всему геному, длина сантиморгана не постоянна. Там, где кроссинговер происходит часто, сантиморганы короткие, а там, где он происходит редко, сантиморганы длинные. Кроме того, различные компании, секвенирующие ДНК, делят человеческий геном на разное число сантиморганов. Кстати, я еще не сказал, что 100 сантиморганов не образуют морган?
Еще одна головоломка: когда я перевел сантиморганы на этом графике в проценты, я обнаружил, что пик распределения расположен не в районе 50%, а в районе 75%. Почему? Моя жена Тэрин объяснила: коммерческие секвенаторы ДНК не могут отличить тот случай, когда есть две общие хромосомы, и тот случай, когда общая хромосома всего одна. (Теперь уже могут. — Прим. науч. ред.) По логике игры в орлянку у двух братьев и/или сестер, как правило, около 50% генома совпадут в одной из двух гомологичных хромосом, около 25% совпадут в обеих и 25% не совпадут совсем. Таким образом, 75% генома совпадают хотя бы один раз, и поэтому пик графика расположен в районе 75%.
. Среднее значение около 1,6 (по найденным мною данным). Для женщин это значение больше, чем для мужчин. В любом случае, утроение — это грубая недооценка числа потенциальных геномов, потому что кроссинговер может произойти (теоретически) в любой точке на протяжении всей цепочки ДНК, что подразумевает несметное число дополнительных возможностей. Подробности см.: Ron Milo and Rob Phillips, “What Is the Rate of Recombination?” Cell Biology by the Numbers, .
. Канеман Д. Думай медленно… Решай быстро. — М.: АСТ, 2013.
. Подробнее об исходе голосования: см. 99,9997% контента социальных сетей в те дни.
. Michael Lewis, Liar’s Poker: Rising Through the Wreckage on Wall Street (New York: W.W. Norton, 1989).
. Nate Silver, The Signal and the Noise: Why So Many Predictions Fail — but Some Don’t (New York: Penguin Books, 2012), 135–37. [Сильвер Н. Сигнал и шум. Почему одни прогнозы сбываются, а другие — нет. — М.: КоЛибри, 2019.]
. В работе над этой главой мне неимоверно помогла Шичжоу Чен, моя бывшая ученица-десятиклассница, которая сейчас превосходит меня в интеллектуальном плане. Заглавие чернового варианта главы было более дерзким, а вступление менее осознанным; Шичжоу помогла мне сократить текст. «Затейливые и забавные примеры, — написала она, — но не совсем полная картина того, что представляет собой страхование». Туше, Шичжоу.
. Emmett J. Vaughan, Risk Management (Hoboken, NJ: John Wiley & Sons, 1996), 5.
. Mohammad Sadegh Nazmi Afshar, “Insurance in Ancient Iran,” Gardeshgary, Quarterly Magazine 4, no. 12 (Spring 2002): 14–16.
. “Lottery Insurance,” This Is Money, July 17, 1999, .
. Шичжоу сделала хорошее замечание: в подобных нишах рынка страхования конкуренция ниже, а наценка выше, чем на крупных рынках, таких как стоматология или недвижимость.
. Шичжоу проницательно добавляет: «Владелец малого бизнеса? Тогда да. Большая фирма? Абсолютно незаконно. Бухгалтерский отдел скорее потратит миллион долларов на “страхование”, чем пять долларов на “лотерею”».
. Laura Harding and Julian Knight, “A Comfort Blanket to Cling to in Case You’re Carrying Twins,” Independent, April 12, 2008, . Оттуда же цитата Дэвида Куо.
. См. похожий анализ: “Insurance: A Tax on People Who Are Bad at Math?” Mr. Money Mustache, June 2, 2011, . Масташ пишет: «Любое страхование — автомобиля, дома, ювелирных украшений, здоровья, жизни — это безумная сфера, управляемая маркетингом, страхом и сомнениями».
. Проверьте на сайте . Мой источник: Vicki Haddock, “Don’t Sweat Alien Threat,” San Francisco Examiner, October 18, 1998, .
. Teresa Hunter, “Do You Really Need Alien Insurance?” Telegraph, June 28, 2000, .
. Я сам придумал эти критерии. Шичжоу одолжила мне свои конспекты учебных дисциплин в бакалавриате, и перечень «характеристик страхуемого риска» немного отличался:
1) потенциальная потеря достаточно значительна, чтобы люди хотели заплатить страховой сбор;
2) убыток и его экономическое значение четко определены и неподконтрольны обладателю страхового полиса;
3) страховка выплачивается достаточно умеренному числу клиентов.
. Две компании такого рода: Insurevents () и National Hole-in-One ().
. Scott Mayerowitz, “After Sox Win, Sofas Are Free,” ABC News, October 29, 2007, .
. Ознакомьтесь с их предложениями: .
. Haddock, “Don’t Sweat Alien Threat.”
. Amy Sohn, “You’ve Canceled the Wedding, Now the Aftermath,” New York Times, May 19, 2016, .
. Ко всему прочему, это поможет расширить ваш бизнес: вы сможете работать своего рода консультантом по рискам. «Специализированная экспертиза — одна из причин, по которой фирмы покупают страховку, — сказала мне Шичжоу. — Когда снимаешь кино, всегда нанимается страховой инспектор, чтобы убедиться, что актеры в безопасности. Иначе в кино было бы больше безумных и бессмысленных взрывов, чем мы наблюдаем сегодня».
. Olufemi Ayankoya, “The Relevance of Mathematics in Insurance Industry,” февраль 2015 г.
. “Loss-of-Value White Paper: Insurance Programs to Protect Future Earnings,” NCAA.org, .
. Andy Staples, “Man Coverage: How Loss-of-Value Policies Work and Why They’re Becoming More Common,” SportsIllustrated.com, January 18, 2016, .
. Громкое имя, не правда ли? Will Brinson, “2017 NFL Draft: Jake Butt Goes to Broncos, Reportedly Gets $500K Insurance Payday,” CBS Sports, April 29, 2017, .
. Можно перечислить целую полку книг на эту тему. Я рекомендую тексты Сары Клифф, журналистки Vox: . Шичжоу рекомендует два выпуска документальной радиопередачи «Эта американская жизнь» от 2009 года: “More Is Less” (№391) и “Someone Else's Money” (№392): .
. Несомненно, основной источник этой главы: David Orrell and Paul Wilmott, The Money Formula: Dodgy Finance, Pseudo Science, and How Mathematicians Took Over the Markets (Hoboken, NJ: John Wiley & Sons, 2017).
. Окей, в моем случае скорее «увязываем случайные вероятности». Уолл-стрит использует два более серьезных подхода. Во-первых, опирается на данные за разные периоды. Во-вторых, смотрит на рыночную цену аналогичных облигаций и учитывает ее при подсчете вероятности дефолта. Второй метод может породить жуткие взаимозависимости и петли обратной связи: вместо того чтобы выносить суждение самостоятельно, вы умножаете эхо мнимой мудрости рынка. Завяжите узелок на память: мы еще вернемся к этой теме.
. Michael Lewis, The Big Short: Inside the Doomsday Machine (New York: W. W. Norton, 2010). [Льюис М. Игра на понижение. Тайные пружины финансовой катастрофы. — М.: Альпина Паблишер, 2019.] Или, если вы предпочитаете не читать, а слушать: “The Giant Pool of Money,” This American Life, episode #355, May 9, 2008A. Этот эпизод включает ключевой подкаст Planet Money.
. Я видел эти эскизы 4 июня 2017 года в прекрасном бельгийском музее Магритта. Советую посетить его, если вы окажетесь в Бельгии и захотите приправить сюрреализмом вашу картошку фри.
. Это общепринятые финансовые термины, которые мне сообщила Джессика Джефферс. Я должен принести ей благодарность за помощь при работе над этой главой. Я шучу всего на 37%, когда говорю, что Джесс — моя кандидатура на пост председателя Совета управляющих Федеральной резервной системы США.
. Еще один важный источник этой главы (в особенности дискуссии о гауссовой копуле): Felix Salmon, “Recipe for Disaster: The Formula That Killed Wall Street.” Wired, February 23, 2009, .
. А также критическая доза сумасшествия (complete damn stupidity).
. См. другой важный источник этой главы: Keith Hennessey, Douglas Holtz-Eakin and Bill Thomas, “Dissenting Statement,” Financial Crisis Inquiry Commission, January 2011, .
. James Surowiecki, The Wisdom of Crowds: Why the Many Are Smarter than the Few and How Collective Wisdom Shapes Business, Economies, Societies, and Nations (New York: Anchor Books, 2004). [Шуровьески Дж. Мудрость толпы. Почему вместе мы умнее, чем поодиночке, и как коллективный разум влияет на бизнес, экономику, общество и государство. — М.: МИФ, 2014.]
. Оррелл и Уилмотт.
ЧАСТЬ IV. СТАТИСТИКА. ИЗЯЩНОЕ ИСКУССТВО ЧЕСТНОЙ ЛЖИ
. Канеман Д. Думай медленно… Решай быстро. — М.: АСТ, 2013.
. Благодарю Ричарда Бриджеса за (1) его помощь в подготовке этой главы и (2) за его платонизм, прагматизм, талант учителя, блестящий ум и доказательство того, что все эти качества могут уживаться в одном человеке.
. Все данные из «Википедии». Ради вас, дорогой читатель, я использую самые надежные источники.
. Loyd Grossman’s. Еще у них есть тикка-масала в банках.
. Моим студентам всегда кажется странным и слишком запутанным возводить разницы в квадрат, складывать и потом извлекать квадратный корень. Почему бы просто не усреднить разности? То, что получится, называется «среднее абсолютное отклонение». Смысл его примерно тот же, что у среднеквадратичного отклонения, но ему не хватает важных теоретических свойств. Для статистических моделей важно, что легко вычислять дисперсии от сумм и произведений случайных величин.
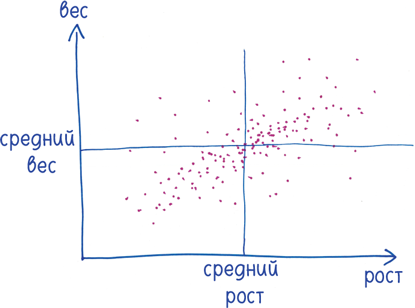
. Окей, пристегнитесь! Пора заняться кое-чем буйническим — это мое слово-гибрид от «буйный» и «технический». Для начала постройте диаграмму разброса данных, скажем рост (координата по горизонтали) и вес (по вертикали). Обозначьте каждого человека точкой.
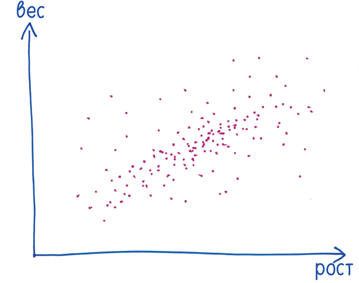
Теперь найдите средний рост и средний вес в этой популяции.
Затем возьмите отдельного человека. Насколько его вес и рост отличаются от средних значений? Если его вес/рост больше средних величин, засчитайте разницу как положительную, если меньше — как отрицательную.
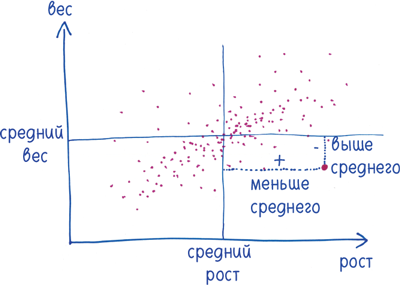
Затем — и это решающий шаг — перемножьте эти два значения. Если человек выше и тяжелее среднего, итог будет положительным. То же самое, если он ниже и легче среднего (потому что минус на минус дает плюс). Но если только одна из величин меньше среднего, результат будет отрицательным (потому что минус на плюс дает минус).
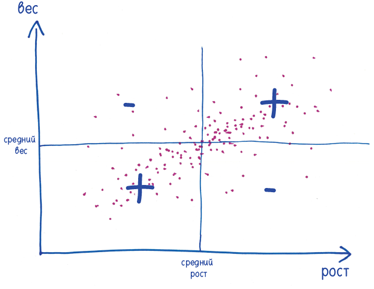
Проделайте эти вычисления для каждой точки, а затем найдите среднее арифметическое всех произведений. Эта величина называется ковариацией (кузина нашей знакомой дисперсии).
Вы почти у финиша! На завершающем этапе поделите это число, чтобы окончательный результат лежал между –1 и 1. (Поделить на что? Ну, подумайте о недостатке ковариации: если рост и вес людей весьма разнообразны, то отклонением от среднего, как правило, будет большее число. Другими словами, ковариация будет больше для неустойчивых величин и меньше для стабильных, вне зависимости от взаимосвязи между ними. Каким образом решить эту проблему? Просто поделите ковариацию на произведение среднеквадратичных отклонений — вы получите корреляцию.)
Уф! Теперь легкий этап: интерпретируем результаты.
Положительная корреляция (например, 0,8) подразумевает, что люди ростом выше среднего, как правило, еще и больше весят. Отрицательная корреляция (например, –0,8) подразумевает обратное: преобладают высокие худые люди или низкорослые толстяки. И наконец, корреляция, близкая к нулю, означает, что никакой значимой взаимосвязи нет. (На самом деле связь может быть, просто более сложная. — Прим. науч. ред.)
. Цит. по книге: “Henry Chadwick,” National Baseball Hall of Fame, . «Каждое движение, — сказал он о бейсболе, — стремительно, словно полет морской птицы». Мой друг Бен Миллер по этому поводу задался вопросом: африканской ласточки или европейской? (Цитата из знаменитого комедийного фильма «Монти Пайтон и Священный Грааль»: «Какова скорость полета порожней ласточки? — Какую ласточку вы имеете в виду — африканскую или европейскую?» — Прим. пер.) (Ласточка — не морская птица. — Прим. науч. ред.)
. Этот рекорд принадлежит отбивающему Брайану Лара из команды West Indies. В 2004 году во время матча с Англией он набрал ровно 400 пробежек без единого аута. Я рад странной статистической перекличке с названием этой главы.
. Цит. по книге: Michael Lewis, Moneyball: The Art of Winning an Unfair Game (New York: W. W. Norton, 2003), 70. Никто не удивится, если я признаюсь, что эта глава в неоплатном долгу перед книгой «Манибол», и, если вы готовы вытерпеть историю бейсбольной статистики (дело десятое, интересна она вам или нет), вы получите удовольствие от этой книги.
. Я взял для примера сезон английской Премьер-лиги, состоящий из 38 игр. Каждая игра длится 90 минут, накинем еще по 10 минут добавленного времени и получим в общей сложности 3800 минут. Двенадцать точек сбора данных в минуту (т.е. каждые 5 секунд) дадут 45 600 точек — все равно меньше, чем 48 000 в бейсболе, но довольно близко.
. Ernest Hemingway, The Old Man and the Sea, Life, September 1, 1952. Над заглавием значилось: «Редакция журнала Life с гордостью представляет вниманию читателей новую великую книгу великого американского писателя, публикуемую впервые и в полном объеме».
. Branch Rickey, “Goodby to Some Old Baseball Ideas,” Life, August 2, 1954. Подзаголовок гласил: «Знаток игры приоткрывает формулу, которая с помощью статистики развенчивает лелеемые мифы и показывает, что побеждает на самом деле».
. E. Miklich, “Evolution of 19th Century Baseball Rules,” 19cBase ball.com, .
. Понадобилось много времени, чтобы решить, сколько болов обеспечивают пробежку. Вначале договорились о трех, потом прошли все числа от девяти до пяти и в конце концов в 1889 году сошлись на четырех. Так и осталось до сих пор.
. Даже тогда обозреватели не вполне принимали их. Просто послушайте журналиста Фрэнсиса Рихтера: «Цифры [для пробежек] не имеют особой ценности или значения. Они зависят всецело от питчера и неподконтрольны отбивающему, и поэтому не нужно рассматривать этот показатель в связи с его индивидуальной работой, за исключением тех случаев, когда они могут косвенно указывать на его способность “пережидать” питчера или “работать” с ним». Bill James, The New Bill James Historical Baseball Abstract (New York: Free Press, 2001), 104.
. Например, в 2017 году лидером лиги был Джои Вотто. Его результат — 134 пробежки при 707 подходах к бите, т.е. 19%.
. В 2017 Алкид Эскобар совершил 15 пробежек при 629 подходах к бите, т.е. 2,4%. Тим Андерсон «побил» этот антирекорд: 13 пробежек при 606 выходах к бите, т.е. 2,1%.
. Будучи учителем математики, я ненавижу это нагромождение статистических показателей, потому что обессилеваю всякий раз, когда кто-нибудь складывает дроби с разными знаменателями. Я всегда хотел, чтобы рассчитали новый вид статистики — «набранные базы делить на выходы к бите», наподобие SLG, за исключением того, что вы учитываете пробежки наравне с синглами. Работая над этой главой, я осознал свою глупость: хотя концепция довольно ясная, этот новый вид статистики будет обладать на практике меньшей предсказательной силой. Судя по данным за 2017 год, коэффициент корреляции для такого показателя составит 0,873. Это меньше, чем у OBP.
. Alan Schwarz, “Looking Beyond Batting Average,” New York Times, August 1, 2004, .
. Например: «Вот бы взять с собой в море великого Ди Маджио, — сказал старик. — Говорят, его отец был рыбаком».
. Scott Gray, The Mind of Bill James: How a Complete Outsider Changed Baseball (New York: Three Rivers Press, 2006). В книге приведено несколько афоризмов Билли Джеймса, в том числе такой: «Всегда кто-то сражается на передовой, а кто-то плетется в арьергарде. Но знания сдвигают саму линию фронта». И еще: «Когда в ходе дискуссии вы приводите точные, неоспоримые факты, дискуссия приобретает совсем иной характер».
. И все же на протяжении 1970-х годов статистика MLB выстраивала рейтинг атакующих игроков по BA, а не по количеству заработанных очков. «Очевидно, — сострил Джеймс, — что цель нападающего состоит не в том, чтобы повысить свой BA».
. Michael Haupert, “MLB’s Annual Salary Leaders Since 1874,” Outside the Lines (Fall 2012), Society for American Baseball Research, . Я немного жульничаю, не учитывая на этом графике инфляцию; например, зарплата Ди Маджио в 1951 году составляла $90 000, что соответствует $800 000 в 2017 году. В любом случае влияние свободных агентов сложно отрицать.
. Pete Palmer, The 2006 ESPN Baseball Encyclopedia, (New York: Sterling, 2006), 5.
. Bill Nowlin, “The Day Ted Williams Became the Last.400 Hitter in Baseball,” The National Pastime (2013), Society for American Baseball Research, .
. Бен Миллер (джентльмен, героический кулинар и неисправимый фанат «Ред Сокс») заметил, что успех Уильямса выходит далеко за рамки этого числа. В 1941 году «его OBP составлял 55,3% — рекордное число для одного сезона за 60 лет. OBP Уильямса за всю его карьеру равен 48,2% — выше нет ни у кого. BA Уильямса за всю карьеру составляет 34,4%, он на шестом месте среди всех игроков, и в этом списке, лишь начиная с 17 места (Тони Гвин), появляются лидеры по BA, игравшие после 1940 года». Как ни крути, Великолепная Заноза (прозвище Уильямса) знал свое дело.
. Bill Pennington, “Ted Williams’s. 406 Is More Than a Number,” New York Times, September 17, 2011, .
. Широко цитируемая статья 2011 года показала опасность стандартных статистических методов. Авторы пришли к абсурдному выводу: прослушивание песни «Битлз» «Когда мне будет шестьдесят четыре» делает студентов моложе. Они не просто ощущают себя моложе. Они действительно молодеют — или так говорят статистики. Это дерзкая, блестящая и заслуживающая внимания статья: Joseph Simmons, Leif D. Nelson, and Uri Simonsohn, “False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant,” Psychological Science 22, no. 11 (2011): 1359–66, .
Из научно-популярных статей я рекомендую: “Daryl Bem Proved ESP Is Real: Which Means Science Is Broken,” Slate, May 17, 2017, .
Кроме того, я чрезвычайно благодарен Кристине Ольсон (наставница единожды — наставница навеки!), Симин Вазир (она откликнулась на мое письмо спустя 17 секунд) и Санджай Шривастава (я цитирую его ближе к концу главы) за их помощь и поддержку при написании этой главы.
. p-значение — это вероятность получить экстремальный результат в случае, если гипотеза, которую проверяет эксперимент, ложна, т.е. на самом деле все результаты чисто случайны.
Или чуть более подробно:
1. Предположим, что мы подпали под власть фантома и что шоколад на самом деле не делает людей счастливыми.
2. Сделаем распределение всех возможных результатов эксперимента. Большинство результатов будут низкосортными, заурядными и вряд ли введут нас в заблуждение. Но несколько фантомов будут свидетельствовать о том, что шоколад резко повышает ощущение счастья.
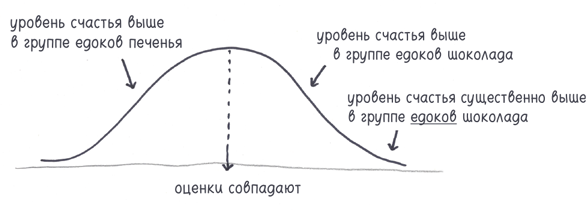
3. Посмотрим, каков перцентиль нашего результата в этом распределении.
Низкое значение (например, 0,03, т.е. 97-й перцентиль) говорит о том, что фантомов мало. Всего лишь 3% ложных результатов будут такими поразительными и обманчивыми. Это крайне низкое значение позволяет предположить, что — возможно — наш результат вовсе не фантомный. Возможно, эффект, который мы исследуем, имеет отношение к действительности.
Строго говоря, такое свидетельство косвенное. 3% — это не вероятность получить тот или иной фантомный результат. Это вероятность того, что вы случайно получите исход, подтверждающий вашу ложную гипотезу.
. Kristina Olson et al., “Children’s Biased Evaluations of Lucky Versus Unlucky People and Their Social Groups,” Psychological Science 17, no. 10 (2006): 845–46, .
. Kristina Olson et al., “Judgments of the Lucky Across Development and Culture,” Journal of Personality and Social Psychology 94, no. 5 (2008): 757–76.
. Ben Orlin, “Haves and Have Nots: Do Children Give More to the Lucky Than the Unlucky?” Yale University, senior thesis in psychology, 2009. Научный руководитель — Кристина Ольсон, которая заслуживает благодарности за все достоинства этой работы и не несет ответственности за ее недостатки.
. Я предположил, что восьмилетние будут восприимчивы к ситуации: отдадут игрушку тем, кому так ужасно не повезло игрушку потерять, но не тем, кого постигла несущественная неудача (например, необходимость играть с нелюбимым одноклассником), в то время как пятилетние будут невосприимчивы к такого рода случаям. p-значение этого эксперимента составило 0,15.
. Горячо рекомендую: .
. Leslie John, George Loewenstein, and Drazen Prelec, “Measuring the Prevalence of Questionable Research Practices with Incentives for Truth Telling,” Psychological Science 23, no. 5 (2012): 524–32, .
. Это не вполне несправедливое сравнение, поскольку даже взломщик p-значения не будет задним числом останавливать исследование при минимальном p-значении. Идея пересчета данных после каждого респондента тоже сомнительна.
. Вначале я подумал, что это звучит глупо. Что-то вроде: «Наши американские горки предназначены для людей ростом от 120 см, но дети придумали уловку: один встает другому на плечи и надевает длинный плащ. Поэтому давайте поднимем планку до 150 см». Затем я прочитал актуальную статью: Daniel J. Benjamin et al., “Redefine Statistical Significance,” PsyArXiv, July 22, 2017, . Она меня переубедила. Похоже на то, что снижение планки с 0,05 до 0,005 будет лучше соответствовать интуитивным байесовским порогам, и для снижения количества ложноположительных результатов требуется лишь умеренное увеличение размеров выборки. Кроме того, следует подчеркнуть, что подходы байесовцев хитроумнее и существенно сложнее, чем я изобразил в этой главе. Вопрос, каким должно быть предварительное суждение, можно обойти, проведя анализ со всем многообразием первоначальных оценок и построив графики общих тенденций. Как бы то ни было, Санджай Шривастава убедил меня, что на самом деле переход к байесианизму не устранит кризиса отсутствия повторяемости, однако может быть полезен по другим причинам.
. Open Science Collaboration, “Estimating the Reproducibility of Psychological Science,” Science 349, no. 6251 (2015): .
. Jay Mathews, “Jaime Escalante Didn’t Just Stand and Deliver. He Changed U. S. Schools Forever,” Washington Post, April 4, 2010, .
. “Mail Call,” Newsweek, June 15, 2003, .
. Jay Mathews, “Behind the Rankings: How We Build the List,” Newsweek, June 7, 2009, .
. Tim Harford, Messy: How to Be Creative and Resilient in a Tidy-Minded World (London: Little, Brown, 2016), 171–73.
. Это не выдумка: Cathy O’Neil, Weapons of Math Destruction: How Big Data Increases Inequality (New York: Broadway Books, 2016), 135–40.
. Jay Mathews, “The Challenge Index: Why We Rank America’s High Schools,” Washington Post, May 18, 2008, .
. Я смотрю американский футбол с семи лет и никогда не понимал рейтинг пасующего. Сейчас я решил, что настало время попробовать. Потребовалось несколько минут, чтобы распутать формулу, но, когда мне это удалось, я увидел, что в ней нет ничего сложного. Во-первых, она начисляет и отнимает очки (1 за ярд, 20 за завершенный пас, 80 за тачдаун и –100 за перехват). Во-вторых, она позволяет вычислить среднее количество очков за попытку паса. И в-третьих, пышным цветом расцветают бессмысленные операции сложения и умножения. Или в виде уравнения:
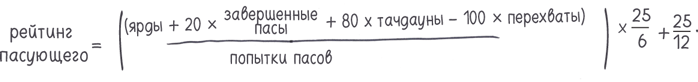
Мы могли бы закончить на этом… однако такая формула может дать отрицательные значения (если перехватов было слишком много), и результат не имеет верхнего предела (в то время как фактический максимум равен 158⅓, и его добились больше 60 квотербеков). Дабы исправить этот изъян, необходимо ограничить число возможных очков по каждой переменной, и тогда получится формула из основного текста книги.
Почему рейтинг пасующего кажется таким запутанным? Как и с большинством жутких формул, роль играют два фактора: (1) она сбивает с толку, потому что в нее входят четыре переменных со странными коэффициентами, к тому же результат каждого умножения ограничен сверху и/или снизу; и (2) кроме того, большинство источников объясняет ее бесполезным, абсурдным и туманным образом. Загляните в «Википедию», чтобы понять, что я имею в виду.
. Mathews, “Behind the Rankings.”
. J. P. Gollub et al., eds., “Uses, Misuses, and Unintended Consequences of AP and IB,” Learning and Understanding: Improving Advanced Study of Mathematics and Science in U. S. High Schools, National Research Council (Washington, DC: National Academy Press, 2002), 187, .
. Согласно этому опросу, больше 20% учителей в стране, преподающих в рамках программы AP, полагали, что «Индекс вызовов» оказал «некое влияние» на количество предлагаемых факультативов AP. В городах и пригородах доля учителей, придерживающихся этого мнения, ближе к трети. Между тем всего 17% считают, что этот рейтинг — «хорошая идея». Steve Farkas and Ann Duffett, “Growing Pains in the Advanced Placement Program: Do Tough TradeOffs Lie Ahead?” Thomas B. Fordham Institute (2009), .
. Valerie Strauss, “Challenging Jay’s Challenge Index,” Washington Post, February 1, 2010, .
В 2006 году, согласно «Индексу вызовов», Истсайдская государственная школа в Гейнсвилле (штат Флорида) заняла шестую строчку в рейтинге по всему США. Однако лишь 13% из почти 600 учеников-афроамериканцев в этой школе обладали навыками чтения на необходимом уровне. В школах, которые заняли 21-е и 38-е место, наблюдались схожие несоответствия. Критики решили: это свидетельствует о том, что неподготовленных студентов загоняют на курсы уровня колледжа, чтобы школу заприметил Newsweek. Источник: Michael Winerip, “Odd Math for ‘Best High Schools’ List,” New York Times, May 17, 2006, .
. John Tierney, “Why High-School Rankings Are Meaningless — and Harmful,” Atlantic, May 28, 2013, .
. Mathews, “Behind the Rankings.”
. Jay Mathews, “I Goofed. But as Usual, a Smart Educator Saved Me,” Washington Post, June 25, 2017, .
. Winerip, “Odd Math for ‘Best High Schools’ List.”
. Jay Mathews, “America’s Most Challenging High Schools: A 30-Year Project That Keeps Growing,” Washington Post, May 3, 2017, .
. Не все ученые согласны с этим. Книга «AP: критическое рассмотрение программы Advanced Placement», вышедшая в 2010 году, излагает общую точку зрения исследователей: рост числа сдающих AP означает уменьшение эффективности этой программы. Один из редакторов Филипп Сэдлер сказал: «Факультативы AP не дают волшебных преимуществ школьникам, которые, возможно, извлекли бы больше пользы, если бы проходили курс обучения не ради увеличения символического капитала колледжа». Источник: Rebecca R. Hersher, “The Problematic Growth of AP Testing,” Harvard Gazette, September 3, 2010, .
. Mathews, “America’s Most Challenging High Schools.”
. Mathews, “The Challenge Index.
. У меня есть скромное предложение Мэтьюсу: вместо того чтобы подсчитывать количество экзаменов, учесть число учеников, получивших по крайней мере 2 балла. Мой опыт (и техасское исследование, которое любит цитировать Мэтьюс) показывает, что 2 балла на экзамене AP означают проблеск интеллекта, сигнал роста. И я не уверен, что типичный однобалльник хоть что-то извлек из занятий. Требование, чтобы школьники преодолели некоторый барьер, устранит стремление принуждать совершенно неподготовленных детей сдавать экзамен.
. Ben Blatt, Nabokov’s Favorite Word Is Mauve (New York: Simon & Schuster, 2017). [Блатт Б. Любимое слово Набокова — лиловый. Что может рассказать статистика о наших любимых авторах. — М.: Бомбора, 2019.]
. Я вычислил «рейтинг величия» на основе данных Goodreads, где читатели проставляют оценку от одной до пяти звездочек. Вначале я подсчитал совокупное количество звездочек, выставленное каждой книге. Для Фолкнера этот показатель составляет от около 1500 («Пилон») до более чем 500 000 («Шум и ярость»). Затем я взял логарифм, который превратил экспоненциальную шкалу в линейную. Корреляция между «величием» и частотностью наречий составляла –0,825. Аналогичный анализ текстов Хемингуэя и Стейнбека дал коэффициенты корреляции –0,325 и –0,433 — существенно, но трудно увидеть на графике. Информацию о частотности наречий я почерпнул у Блатта, а мой метод представляет собой вариацию предложенного им. (Он использовал количество оценок вместо количества звездочек; результат был очень близок к моему.)
. Jean-Baptiste Michel et al., “Quantitative Analysis of Culture Using Millions of Digitized Books,” Science 331, no. 6014 (2011): 176–82, .
Характерная цитата: «Один человек не в силах прочесть весь корпус целиком. Если вы попытаетесь прочесть хотя бы тексты за 2000 год с разумной скоростью 200 слов в минуту без перерыва на еду и сон, это займет у вас 80 лет. Количество букв больше, чем нуклеотидов в человеческом геноме. Если записать все буквы в строчку, она будет в десять раз длиннее, чем расстояние от Земли до Луны».
. Patricia Cohen, “In 500 Billion Words, New Window on Culture,” The New York Times, December 16, 2010, .
. Мишель и Эйден пишут (курсив мой): «Чтение небольших подборок тщательно отсортированных работ позволяет ученым сделать убедительные выводы о тенденциях человеческого мышления. Однако такой подход редко позволяет точно измерить глубинные явления».
. Virginia Woolf, A Room of One’s Own (1929). [Вулф В. Своя комната. — М.: МИФ, 2019.]
. Попробуйте сами: .
. На сайте .
. Moshe Koppel, Shlomo Argamon, and Anat Rachel Shimoni, “Automatically Categorizing Written Texts by Author Gender,” Literary and Linguistic Computing 17, no. 4 (2001): 401–12, .
. Shlomo Argamon et al., “Gender, Genre, and Writing Style in Formal Written Texts,” Text 23, no. 3 (2003): 321–46, .
. Justin Tenuto, “Using Machine Learning to Predict Gender,” CrowdFlower, November 6, 2015, .
. Cathy O’Neil, “Algorithms Can Be Pretty Crude Toward Women,” Bloomberg, March 24, 2017, .
. В книге «Своя комната» Вулф пишет: «Тяжестью, поступью, ритмом мужской ум слишком отличается от [женского], чтобы ему удалось перенять от него что-то существенное. <…> Возможно, взявшись за перо, женщина прежде всего обнаружила, что ей не годится существующее построение фразы». Хотя ей нравится этот мужской стиль («быстрый, но не неряшливый, выразительный, но не манерный»), она добавляет: «такие фразы не годились женщине». «Шарлотта Бронте, при всем ее великолепном даре прозаика, спотыкалась и падала с этим неуклюжим оружием. <…> Джейн Остин посмотрела, рассмеялась и придумала свою собственную, идеально естественную, стройную фразу и никогда не отступалась от нее. Поэтому она сказала бесконечно больше, чем Шарлотта Бронте, хотя обладала меньшим талантом».
. Frederick Mosteller and David Wallace, “Inference in an Authorship Problem,” Journal of the American Statistical Association 58, no. 302 (1963): 275–309.
. В буквальном смысле слова. Блатт пишет: «Они взяли копию каждого эссе и вырезали все слова по отдельности, а затем разложили в алфавитном порядке (вручную). Мостеллер и Уоллес пишут: “…неосторожный выдох поднял вихрь конфетти и сделал нас заклятыми врагами”».
Я был чрезвычайно близок к тому, чтобы назвать эту главу «Вихрь конфетти и заклятый враг».
. Sarah Allison et al., “Quantitative Formalism: An Experiment,” Stanford Literary Lab, pamphlet 1, January 15, 2011, . Я люблю эту статью. По правде говоря, я рекомендую все прочитанные мною статьи Лаборатории литературоведения Стэнфорда. Они похоже на старые мультфильмы студии Pixar: ни одного промаха.
ЧАСТЬ V. НА ПОРОГЕ. СИЛА ОДНОГО ШАГА
. Вы можете обойти это правило, если совершаете много транзакций одновременно. Закупка 100 000 карандашей на сумму $50 438,71 означает, что каждый карандаш вы купили за $0,5043871. Финансовые учреждения, осуществляющие огромное количество транзакций в день, часто оперируют крошечными долями цента.
. На самом деле он не формулировал вопрос напрямую: «Нет ничего полезнее воды, но на нее почти ничего нельзя купить, почти ничего нельзя получить в обмен на нее. Напротив, алмаз почти не имеет никакой потребительной стоимости, но часто в обмен на него можно получить очень большое количество других товаров».
Adam Smith, An Inquiry into the Nature and Causes of the Wealth of Nations (1776), book I, chapter IV, paragraph 13, accessed through the online Library of Economics and Liberty: . [Смит А. Исследование о природе и причинах богатства народов. — М.: Эксмо, 2016.]
. Основной источник этой главы — чудесная книга: Agnar Sandmo, Economics Evolving: A History of Economic Thought (Princeton, NJ: Princeton University Press, 2011). [Сандмо А. Экономика: история идей. — М.: Издательство Института Гайдара, 2019.]
. Campbell McConnell, Stanley Brue, Sean Flynn, Economics: Principles, Problems and Policies, 19th ed. (New York: McGraw-Hill Irwin, 2011). [Макконнелл Кэмпбелл Р., Флинн Шон Масаки, Брю Стэнли Л. Экономикс: принципы, проблемы и политика. — М.: Инфра-М, 2018.] Цитата о плодородной земле: 7.1, Law of Diminishing Returns, .
. Майкл Торнтон отмечает (и я смиренно благодарю его за помощь в работе над главой), что эта аналогия упускает некоторые тонкости. Неоднородная почва может идеально подходить для выращивания нескольких сельскохозяйственных культур, которым требуются разные условия, и фермеры могут применять определенные приемы (например, севооборот), чтобы улучшить качество почвы.
. William Stanley Jevons, “Brief Account of a General Mathematical Theory of Political Economy,” Journal of the Royal Statistical Society, London 29 (June 1866): 282–87, .
. Снова Джевонс. Его приятно цитировать. Эта глава доставила мне много радости.
. Для освежения памяти я обратился к конспектам лекций Майкла Бржезински, доцента факультета экономики Варшавского университета: .
. Фраза из видеоролика Mankiw’s Ten Principles of Economics, Translated, который перепахал меня, когда я первый раз увидел его в студенческие годы. Посмотрите сами на сайте: .
. Сандмо А. Экономика: история идей. — М.: Издательство Института Гайдара, 2019.
. Там же.
. Цитата из «Википедии». Тсс, никому не говорите.
. Джевонс воплотил эту схему. Он предсказал, что Британия скоро исчерпает свои запасы угля, и утверждал, что взлеты и падения бизнес-цикла происходят из-за перепадов температуры, вызванных появлением пятен на Солнце. Окей, он ошибался по обоим пунктам, но мы знаем об этом именно благодаря введенным им методам.
Вальрас, напротив, был немного антиэмпириком. Его точка зрения заключалась в том, что вы должны, во-первых, отфильтровать хаотичные детали реальности, чтобы прийти к чистым количественным концепциям. Во-вторых, вы должны оперировать этими математическими абстракциями и рассуждать о них. В-третьих, можно сказать с опозданием, вы вспоминаете о практических применениях. «Мы не должны возвращаться к реальности, — писал Вальрас, — пока не построим научную теорию». По мнению Вальраса, «наука» очень далека от действительности. Если сейчас вы встретите экономиста, который до сих пор так думает, просто действуйте по следующему незамысловатому алгоритму: (1) вскиньте руки; (2) начните рычать; (3) если экономист продолжит наступление, надерите ему уши. Помните: эти экономисты боятся нас настолько же, насколько мы боимся их.

. Эта мысль напрямую позаимствована из книги Сандмо.
. Я не шучу. Два знаменитейших бельгийца — вымышленные персонажи: Эркюль Пуаро и Тинтин. Лично я считаю, что это очко в пользу Бельгии. Известные исторические личности не приносят ничего, кроме неприятностей.
. Я почерпнул исторические сведения о налогообложении в США из книги: W. Elliot Brownlee, Federal Taxation in America: A History, 3rd ed. (Cambridge: Cambridge University Press, 2016).
. Пороговая сумма ($800) оказалась довольно близка к среднему доходу американских семей ($900, по данным Браунли). Довольно впечатляюще, учитывая, что именно этот дротик правительство метнуло вслепую. Кроме того, я должен отметить, что налогового разряда 0% на самом деле не существовало; правильнее сказать, что доходы вплоть до $800 были освобождены от налога. Математические выкладки те же самые.
. W. Elliot Brownlee, Federal Taxation in America: A History, 3rd ed. (Cambridge: Cambridge University Press, 2016).
. W. Elliot Brownlee, Federal Taxation in America: A History, 3rd ed. (Cambridge: Cambridge University Press, 2016).
. Данные из «Википедии»: .
. Система Джей Джея подразумевала знание математического анализа, так что Джей Джей был незаурядным учеником. В своей системе (в отличие от более простой, которую я иллюстрирую) он переходил от нескольких дискретных скачков ставки к непрерывно меняющемуся верхнему налоговому разряду, чья формула включала натуральный логарифм. Часто быть учителем означает упрощать мир, чтобы ваши ученики могли понять его; здесь, похоже, ситуация была обратной.
. The New Spirit (Walt Disney Studios, 1942). Посмотрите этот чудесный мультфильм: .
. Да, Revolver лучше всех. Попробуйте только поспорить, фанаты Rubber Soul!
. Речь идет о предельной налоговой ставке 95%, поэтому Джордж Харрисон слегка занижал свои доходы.
. Astrid Lindgren, “Pomperipossa in Monismania,” Expressen, March 3, 1976. Мне помог перевод Леннарта Билена: .
. “Influencing Public Opinion,” AstridLindgren.se, accessed September 2017, .
. Конечно, именно так работает текущий налог на заработную плату, предназначенный для финансирования социального обеспечения и медицины. Вы платите 15% от первых $120 000 и ничего сверх того.
. После того как я написал эту жизнерадостную строчку, я обнаружил ее язвительного двойника. Горячо любимый мною Хорхе Луис Борхес в минуту несвойственного ему цинизма сказал: «Демократия — это злоупотребление статистикой».
. «Записки федералиста», № 68 (Александр Гамильтон). Раз уж я начал сыпать именами горячо любимых фигур американской истории, я выражу благодарность Джоффу Кослигу (такому конституционному патриоту, что фоновая музыка в его голове — это “You're a Grande of Flag”) за помощь в работе над этой главой. Кроме того, я хочу поблагодарить Джереми Куна и Чжи Чэня за их ценную помощь.
. Я почерпнул эти сведения, как и 93% моих знаний о Конституции, от Акила Рида Амара. В частности, из книги Akhil Reed Amar, America’s Constitution: A Biography (New York: Random House, 2005), 148–52. График построен на основе данных из «Википедии». (А откуда бы еще им взяться?)
. Тезис взят из той же книги: Амар, «Конституция Америки». Автор идет дальше, утверждая, что Коллегия выборщиков не просто благоприятствовала рабовладельческим штатам (что, в общем-то, бесспорно), но была создана отчасти именно для этого. Такая позиция вызвала определенную критику, в том числе статью с энергичным заголовком «Нет! Коллегия выборщиков не имеет отношения к рабству!». Gary L. Gregg II, No! The Electoral College Was Not about Slavery!, Law and Liberty, January 3, 2017, .
Внесу свою лепту: было бы глупо утверждать, что рабство было единственным фактором, который способствовал созданию Коллегии выборщиков. Но, по-моему, этого никто и не утверждает. На с. 155 Амар пишет: «Прямые президентские выборы в 1787 году были обречены по трем основным причинам: информационные барьеры, федерализм и рабство». Между тем идея о том, что рабство не сыграло никакой роли, на мой дилетантский взгляд, абсолютно ошибочна. 19 июля 1787 года Джеймс Мэдисон поднимал этот вопрос: «Прямое волеизъявление народа <…> было сопряжено с одной сложностью. В северных штатах существенно бóльшая доля граждан обладала избирательным правом, чем в южных; и они могли лишиться возможности повлиять на исход выборов из-за негров. Коллегия выборщиков устранила эту сложность…»
25 июля Мэдисон снова затронул эту тему, однако на сей раз он одобрил прямое голосование и не скрывал своих симпатий, сказав: «Будучи гражданином Южных штатов, он был готов принести эту жертву». Вы можете ознакомиться с деталями самостоятельно в «Записках о дебатах в Федеральном собрании»: .
Еще одно доказательство того, что преимущество рабовладельцев было отличительной чертой, а не сбоем системы: в первом инаугурационном послании в 1833 году южанин Эндрю Джексон предложил заменить Коллегию выборщиков прямым всенародным голосованием, но лишь в том случае, если сохранится неравномерность учета голосов. Источник: Akhil Reed Amar, America’s Constitution: A Biography (New York: Random House, 2005).
. Я взял данные переписи из «Википедии» и перераспределил количество мест в Палате представителей пропорционально числу свободных граждан в каждом штате.
. Кослиг сообщил мне, что когда-то символика цветов была прямо противоположной: синий означал не демократов, а республиканцев, и наоборот. Схема сменилась в 1990-х и закрепилась в 2000-х. Подробности вы можете прочесть в забавной заметке: Jodi Enda, “When Republicans Were Blue and Democrats Were Red,” Smithsonian.com, October 31, 2012, .
. Даже это не так просто, как может показаться. Возьмем в качестве примера выборы 2016 года: демократы набрали 46,44% голосов — округляем до 50% (получаем пять голосов выборщиков), а республиканцы 44,92% — округляем до 40% (получаем четыре голоса выборщиков). Но это всего девять голосов. Кто получит еще один? Можно отдать его либертарианцам, но их результат (3,84%) довольно далек от 10%. Вероятно, логичнее отдать последний голос выборщика партии, которая оказалась ближе к тому, чтобы заработать его статистически — в нашем случае, республиканцам, которым не хватило всего 0,08%.
. Как отмечает Кослиг, иная динамика в штатах, которые отдают предпочтение одной партии на президентских выборах и другой — на голосовании в Законодательное собрание штата. В последние годы несколько подобных штатов рассматривали возможность распределять голоса выборщиков таким же способом, как Небраска и Мэн, чтобы правящая партия штата захватила часть голосов выборщиков у соперника.
. Nate Silver, “Will the Electoral College Doom the Democrats Again?” FiveThirtyEight, November 14, 2016, .
. Сильвер указывает: «Единственное существенное исключение было в первой половине XX века, когда республиканцы имели устойчивое преимущество в Коллегии выборщиков, потому что демократы теряли огромное количество голосов на Юге… Вопрос состоит в том, наступил ли для демократов период сродни эпохе “Сплоченного Юга”, с поправкой на то, что их избиратели сосредоточены в более урбанизированных прибрежных штатах…»
Сильвер склонен ответить отрицательно. Время покажет, прав ли он.
. Он разработан профессором Акилом Ридом Амаром (в колледже я записался на его превосходный курс конституционного права) и его братом, профессором Викрамом Амаром.
. Источник: «Википедия», конечно. Кроме того, я благодарен Дэвиду Клампу и Валуру Гуннарсону за щекочущую мозг обратную связь по этой главе.
. Эта история, график и, по правде говоря, большая часть математики в этой главе взяты из незаменимой книги: James Gleick, Chaos: Making a New Science (New York: Viking Press, 1987). История о Лоренце на с. 17–18. [Глейк Дж. Хаос: создание новой науки. — М.: Амфора, 2011.]
. Хорошо, в XVII веке не было «метров». Это приближение — современный пересчет, и оно справедливо только для довольно малых колебаний. Тем не менее поразительно, что длительность цикла не зависит от угла отклонения: быстрые колебания с большой амплитудой займут примерно столько же времени, сколько более медленные с меньшей амплитудой.
. Проверьте сами, потрясающий симулятор: . Серьезно: если вы просматриваете концевые сноски в поисках какого-то неведомого вдохновения, то вот оно.
. Siobhan Roberts, Genius at Play: The Curious Mind of John Horton Conway (New York: Bloomsbury, 2015).
На с. xiv-xv Робертс цитирует музыканта Брайана Ино: «Вся система настолько прозрачна, что не должно быть никаких сюрпризов, но на самом деле их много: сложность и “органичность” эволюции точечных узоров совершенно не поддается прогнозированию». На с. 160 он цитирует философа Дэниела Деннета: «Я думаю, что “Жизнь” должна стать пищей для размышления на каждой кухне».
. Michael Lewis, The Undoing Project: A Friendship That Changed Our Minds (New York: W. W. Norton, 2016), 101.
. Kim Stanley Robinson, The Lucky Strike (1984). Отличный рассказ. Я прочел его в книге: Harry Turtledove, ed., The Best Alternate History Stories of the 20th Century (New York: Random House, 2002).Кроме того, я не могу не упомянуть мой любимый рассказ в жанре альтернативной истории: Orson Scott Card, Pastwatch: The Redemption of Christopher Columbus (New York: Tor Books, 1996).
. Сложно поверить, что Трумэн не отдавал себе в этом отчета, но, похоже, это так. Послушайте отличный подкаст: “Nukes,” Radiolab, April 7, 2017, .
. Mariko Oi, “The Man Who Saved Kyoto from the Atomic Bomb,” BBC News, August 9, 2015, .
. В 1931 году Уинстон Черчилль опубликовал эссе «Если бы Ли НЕ выиграл битву при Геттисберге». Он говорит от имени историка, живущего в альтернативном мире, где победила Конфедерация; затем он пишет «альтернативную» версию событий, пытаясь представить, как выглядела бы жизнь в нашем мире. Его выводы представляются мне глупыми и наивными, но все-таки я не никогда не спасал цивилизацию от нацистов, поэтому вы не обязаны ко мне прислушиваться. .
. Ta-Nehisi Coates, “The Lost Cause Rides Again,” Atlantic, August 4, 2017, .
. Отчасти эта дискуссия вдохновлена книгой: Michael Lewis’s The Undoing Project, 299–305.
. Ключевая идея теории хаоса состоит в том, что многие системы нарастающей сложности описываются простыми правилами. Возможно — и здесь я соскальзываю в область кухонных полуночных разговоров — есть способ сформулировать несколько детерминистских правил, которые лежат в основе (принципов) истории. Мы могли бы разработать игрушечные модели, чтобы понять степень чувствительности истории к начальным условиям и уровень случайности, как это сделал Эдвард Лоренц, построив свою метеорологическую модель.
. Benoit Mandelbrot, “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension,” Science 156, no. 3775 (1967): 636–38.
. Alan Moore and Eddie Campbell, From Hell (Marietta, GA: Top Shelf Productions, 1999), appendix II, 23. [Мур А., Кэмпбелл Э. Из ада. — СПб.: XL Media, 2018.]
. В научно-фантастическом рассказе Урсулы Ле Гуин «Человек из племени людей» главный герой стремится понять обширную историю цивилизации под названием Хайн: «Теперь он знал, что историки не изучают историю. Ни одно человеческое сознание не могло объять историю Хайна: три миллиона лет… бесчисленные короли, империи, изобретения, миллиарды жизней в миллионах стран, монархии, демократии, олигархии, анархии, века хаоса и века порядка, один пантеон богов за другим, бесконечные войны и мирные времена, поразительные открытия и забвения, бессчетные ужасы и триумфы, бесконечное повторение непрестанной новизны. Какой смысл пытаться описать течение реки в конкретный момент времени, и в следующий, и в следующий, и в следующий, и в следующий? Ты надорвешься. Ты скажешь: “Это великая река, и она течет по этой земле, и мы назвали ее Историей”».
О, я люблю этот отрывок.
Ursula Le Guin, Four Ways to Forgiveness (New York: HarperCollins, 1995), 124–25.
. Я умыкнул этот отличный образ у Валура Гуннарсона.

