Варвары у врат науки
Кризис p-значения
Ура! Пришло время забавных научных фактов!
Для начала: знаете ли вы, что с большей вероятностью будете списывать на экзамене, если до этого прочтете пассаж, доказывающий, что свободы воли не существует?

Или что после того, как вы поставите вплотную две точки на бумаге в клеточку, вы почувствуете бóльшую приязнь к родственникам, чем если поставите две точки далеко друг от друга?
Или что определенные «силовые позы» могут подавлять гормоны стресса и повышать уровень тестостерона, и окружающие будут считать вас более уверенным в себе и представительным?

Я не выдумываю. Это подлинные исследования, выполненные настоящими учеными, одетыми в настоящие лабораторные халаты и/или джинсы. Они основаны на теоретических выкладках, подтверждены экспериментами и одобрены независимыми рецензентами. Исследователи руководствовались научной методикой и не прятали в рукаве джокеров.
Тем не менее эти три исследования — и десятки других, например в таких отдаленных друг от друга областях, как маркетинг и медицина, — теперь вызывают вопросы. Они могут быть ошибочными.
В различных науках наступил кризис. Многие ученые десятилетиями выкладывались по полной и обнаружили, что теперь работа всей их жизни висит на волоске. Виною тому не обман, или отсутствие целостности, или чрезмерное количество абзацев, опровергающих свободу воли. Болезнь гнездится глубже, в общих статистических методах, составляющих основу исследовательского процесса. Речь идет о коэффициенте, который сделал современную науку возможной — и теперь угрожает ее стабильности.
1. Под властью призрака
Каждый научный эксперимент ищет ответ на какой-то вопрос. Существуют ли гравитационные волны? Ненавидят ли миллениалы финансовую устойчивость? Может ли этот новый препарат вылечить от антипрививочной паранойи? Вне зависимости от вопроса есть два возможных ответа («да» и «нет») и, учитывая неизбежную ненадежность данных, два возможных исхода («вы правы» и «вы ошиблись»). Таким образом, результаты экспериментов можно поделить на четыре категории:
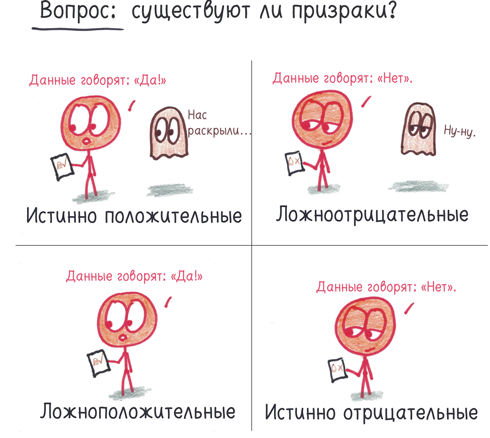
Ученые хотят добиться истинно положительных результатов. Их называют «открытия»: вам вручают ништяки типа Нобелевских премий, любимый человек готовит вам смузи, ваши изыскания продолжают получать финансирование.
Истинно отрицательные результаты воодушевляют меньше. Вам казалось, что вы уже помыли полы и постирали белье, но вдруг вы осознали, что вам это просто примерещилось. Вы узнали правду, но лучше бы она была другой.
Ложноотрицательные результаты раздражают. Вы искали потерянные ключи в нужном месте, но почему-то они все равно не нашлись. Вы никогда не узнаете, насколько близок был успех.
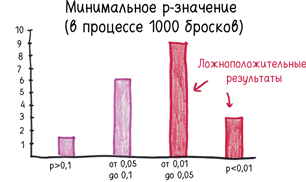
Ложноположительные результаты самые пугающие. Это фантомы: ложь, которая в один пригожий день может сойти за истину. Они сеют смуту в науке, годами таятся незамеченными в научной литературе и влекут за собой тонны впустую потраченного времени. Наука — это непрерывный поиск истины, поэтому ложноположительных результатов невозможно избежать, но крайне важно свести их к минимуму.
Именно тогда на помощь приходит p-значение. Его цель — выявить фантомы.
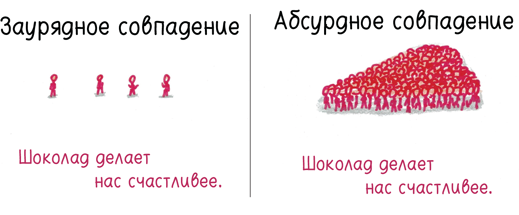
В качестве иллюстрации проведем эксперимент: делает ли шоколад людей счастливее? Наугад разделим респондентов на две равные группы. Пусть одни едят шоколадные батончики, а другие хрустящее печенье. Затем мы попросим их оценить, насколько они счастливы, по шкале от 1 (страдание) до 5 (блаженство). Наша гипотеза: едоки шоколада выставят более высокие баллы.
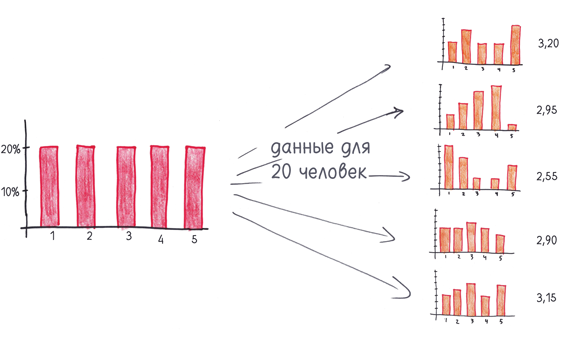
Но есть определенная опасность. Даже если шоколад не влияет на уровень счастья, респонденты из первой группы могут выставить более высокие оценки. Например, взгляните, что произошло, когда я сгенерировал пять случайных наборов данных для одной и той же группы респондентов.
Из-за стечения обстоятельств две теоретически одинаковые группы могут продемонстрировать очень разные результаты. Что, если «шоколадная» группа выставит более высокие оценки по чистой случайности? Как мы отличим подлинное повышение уровня счастья от бессмысленного фантома?
Для того чтобы распознать фантомы, p-значение учитывает три фундаментальных признака:
1. Насколько велико отличие? Незначительное отличие (скажем, 3,3 против 3,2) скорее говорит о случайном совпадении, чем существенная разница (скажем, 4,9 против 1,2).

2. Насколько велик набор данных? Выборка из двух человек не внушает особого доверия. Может быть, я случайно дал шоколадку восторженному любителю жизни, а хрустящее печенье — неблагодарному нигилисту. Но в выборке из 2000 человек, случайным образом разделенной пополам, индивидуальные различия должны стираться. Даже небольшой разрыв (3,08 против 3,01) вряд ли может быть случайным.
3. Дисперсия внутри каждой группы. Если разброс оценок широк и дисперсия высока, разница в результатах двух групп легко могла быть продиктована случайностью. Но если оценки стабильные и дисперсия низкая, то даже небольшая разница, скорее всего, неслучайна.
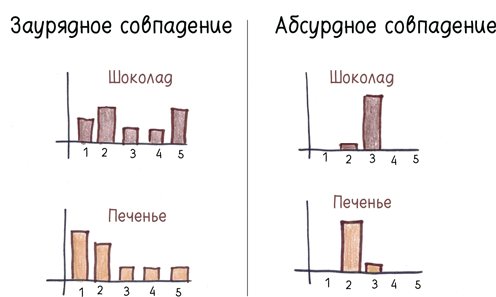
Вся эта информация сводится к p-значению — одному числу между нулем и единицей, своего рода оценке абсурдности совпадения. Чем меньше это число, тем абсурднее полагать, что результаты получены в силу чистой случайности. Близкое к нулю p-значение говорит о том, что совпадение настолько абсурдно, что, возможно, это никакое и не совпадение.
(Чуть больше технических деталей вы найдете в примечании.)

Некоторые p-значения легко интерпретировать. 0,000001 означает, что фантомный результат может получиться случайно в одной из миллиона попыток. Такие совпадения настолько редки, что взаимосвязь почти наверняка есть — в нашем случае шоколад делает людей счастливее.
Между тем p-значение, равное 0,5, означает, что вероятность фантомного результата 1 к 2. Такое происходит… ну, через раз. Подобные результаты повсеместны, словно сорняки. Так что в нашем случае, похоже, шоколад не влияет на уровень счастья.
Между этими ярко выраженными случаями лежит спорная территория. Как насчет p-значения 0,1? А как насчет 0,01? Говорят ли эти числа о том, что мы ловим фантомы или наши результаты достаточно экстремальные и, возможно, это вовсе не фантомы? Чем ниже p-значение, тем лучше; но ниже — это насколько низко?
2. Отладка фильтра фантомов
В 1925 году специалист по статистике по имени Р. А. Фишер опубликовал книгу под названием «Статистические методы для исследователей». В ней он провел черту на песке: 0,05. Иными словами, будем отфильтровывать 19 из 20 фантомов.
Зачем допускать оставшийся 20-й фантом? Ну, вы можете установить порог ниже 5%, если вам угодно. Сам Фишер предпочитал 2% или 1%. Но этот отсев ложноположительных результатов влечет за собой новый риск: ложноотрицательные. Чем больше фантомов вы изгоняете, тем больше истинных результатов может заодно пойти под нож.
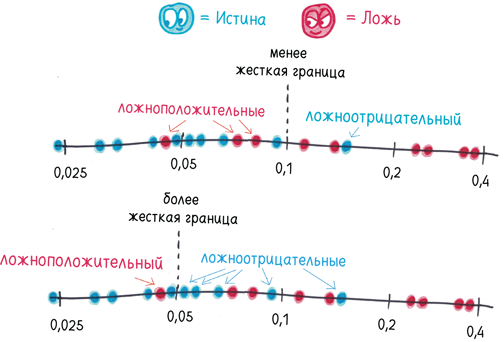
Предположим, вы хотите выяснить, выше ли мужчины ростом, чем женщины. Подсказка: да. Но что, если ваша выборка порождает фантомы? Что, если вы возьмете высоких женщин и низкорослых мужчин и получите среднюю разницу всего один или два дюйма? Тогда строгий порог p-критерия может забраковать результат как фантом, даже если сам по себе он вполне подлинный.
Число 0,05 представляет собой компромисс между заключением в тюрьму ни в чем не повинных и освобождением виновных.
Сам Фишер никогда не имел в виду, что 0,05 — железобетонный критерий. В своей собственной карьере он проявлял замечательную гибкость. Однажды в одной и той же статье он одобрил p-значение 0,089 («есть некоторые основания подозревать, что распределение… не вполне случайно»), но отверг 0,093 («такая взаимосвязь, если она существует, недостаточно сильна, чтобы проявляться значительно»).
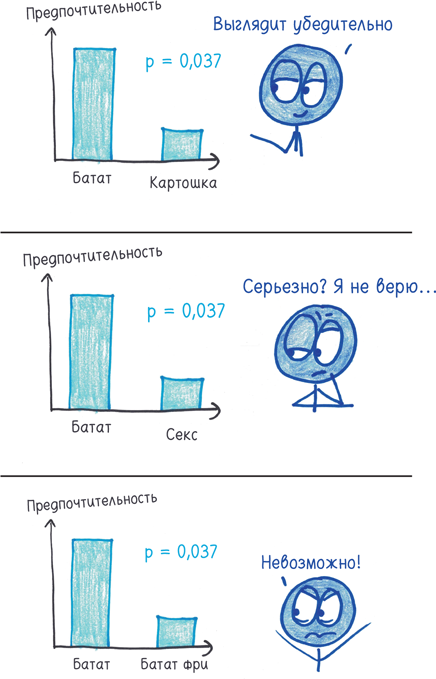
На мой взгляд, это осмысленный подход. Глупое постоянство — мелкий бес начинающих статистиков. Если вы скажете мне, что благодаря мятным леденцам после обеда исчезает неприятный запах изо рта (p = 0,04), я буду склонен вам поверить. Если вы скажете, что мятные леденцы лечат остеопороз (p = 0,04), я буду не столь убежден. Я признаю, что 4% — низкая вероятность. Но, я полагаю, еще менее вероятно, что на протяжении десятилетий наука упускала из виду стойкую связь между здоровьем скелета и «Тик-таком».
Новые данные необходимо сопоставлять с нашими знаниями. Не все 0,04 созданы равными.
Ученые это понимают. Но в области, которая гордится стандартизацией и объективностью, сложно отстаивать нюансы персонифицированных суждений. И в XX веке в гуманитарных науках наподобие психологии и медицины статус границы «5%» постепенно эволюционировал от «предложения» к «директиве» и «промышленному стандарту». p = 0,0499? Значимо.А p = 0,0501? Извините, попытайте счастья в следующий раз.
Означает ли это, что 5% принятых результатов получены в силу случайности? Не совсем. На самом деле все наоборот: 5% фантомов удовлетворяют критерию значимости. Казалось бы, разницы нет, но это не так.
Все гораздо страшнее.
Представьте, что p-значение — страж у врат цитадели науки. Он впускает истинно положительные результаты и отражает атаки варваров, то есть ложноположительных результатов. Мы знаем, что 5% из них проскользнут внутрь, но в общем и целом это, похоже, неплохо.
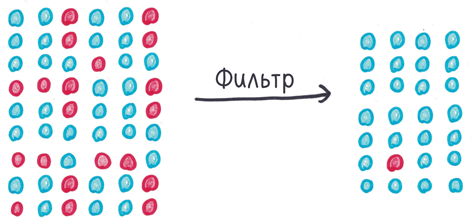
Но что, если атакующих варваров в 20 раз больше, чем наших солдат? Тогда 5% вторженцев — это ровно столько же, сколько всех бойцов на стороне цивилизации.
Хуже того, что, если на каждого верного долгу солдата приходится сотня варваров? Тогда 5% атакующих подавят всю армию защитников цивилизации. Цитадель заполонят ложноположительные результаты, а истинно положительные будут жаться по углам.
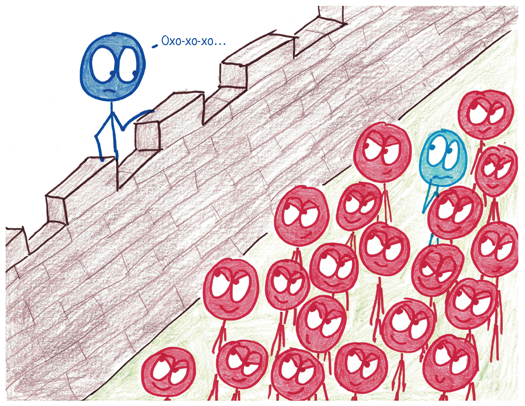
Таким образом, опасность резко возрастает, когда ученые проводят чересчур много исследований, где истинный ответ отрицательный. Пение под фонограмму превращает вас в блондина? Начнется ли кислотный дождь, если вы наденете клоунские башмаки? Проведите миллион мусорных исследований, и 5% пройдут фильтр. Их будет 50 000. Они захлестнут научные журналы, замелькают в заголовках новостей и сделают ленту «Твиттера» еще менее читабельной, чем обычно.
Если это никого особо не расстраивает, ситуация еще больше ухудшается. Сами того не желая, ученые снабдили варваров абордажными крюками и таранами.
3. Как плодятся фантомы?
В 2006-м психолог по имени Кристина Ольсон начала записывать проявления своеобразной тенденции: дети предпочитают счастливчиков неудачникам. Ольсон и ее коллеги обнаружили такие предпочтения у представителей разных культур в возрасте от трех лет вплоть до вступления во взрослую жизнь. Тезис был справедлив и для тех, кто потерпел мелкие неудачи (например, шлепнулся в грязь), и для тех, кто пострадал от катастроф (например, торнадо). Эффект был стойким и убедительным — истинно положительным.
Затем в 2008 году Ольсон согласилась стать научным руководителем дипломной работы нерадивого 21-летнего студента по имени я. Благодаря ее огромной помощи я придумал скромное дополнительное исследование: будут ли пяти- и восьмилетние дети отдавать больше игрушек счастливчикам, чем неудачникам?
Я опросил 46 детей. Ответ был отрицательным.
Если я и выявил какую-то тенденцию, то она была обратной: мои респонденты, похоже, охотнее делились с несчастными, чем со счастливыми. В отличие от «забавных научных фактов» это казалось очевидным: естественно, вы отдадите игрушку тому, кто ее лишился. Мне нужно было выжать из эксперимента 30 страниц, и я посмотрел на свои данные. Каждый испытуемый ответил мне на восемь вопросов, и я проверил множество условий. В итоге я мог бы разделить результаты на категории несколькими способами.
Здесь, в неброских столбцах чисел, зародилась опасность.
Судя по всему, мой тезис был варваром у ворот. Важное для исходной гипотезы p-значение было значительно выше 0,05. Но, если быть непредвзятым, надо было бы рассмотреть и другие возможные постановки задачи. Что, если я буду рассматривать исключительно пятилетних? Или только восьмилеток? Или только счастливых реципиентов? Или только неудачников? Играет ли значение половая принадлежность? Что, если восьмилетние девочки более отзывчивы по отношению к детям, которым они выставили четверку по шестибалльной шкале приязни, чем пятилетние мальчики?
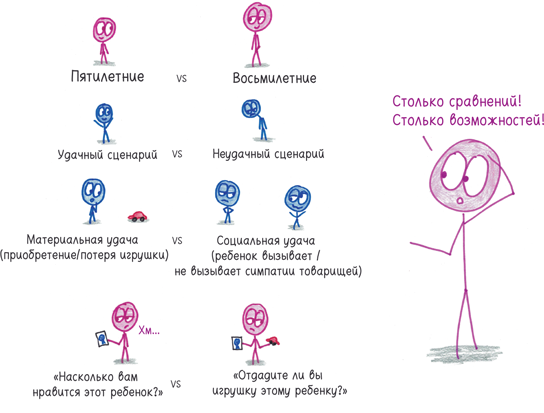
Что, если, что, если, что, если…
По-разному дробя полученные данные, я мог превратить один эксперимент в двадцать. Уже не играло роли, отсеет ли p-значение моего варвара единожды, дважды или десять раз. Я мог маскировать его так или этак, пока он наконец не прокрадется в цитадель.
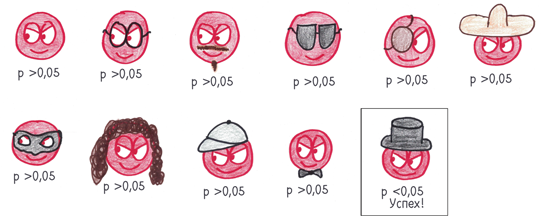
Вот так вот и рождается, возможно, величайший методологический кризис нашего юного столетия: хакерский взлом p-значения. Дайте группе правдолюбивых ученых возможность принять участие в гонке за положительными результатами, где победитель получает все, и наблюдайте, как они, наступая на горло собственной песне, ведут себя как 21-летний я, рационализируя хитроумные решения. «Ну, может, я перепроверю цифры…» «Я же знаю, это правильный результат; просто мне нужно исключить резко выделяющиеся данные…» «О, если я проконтролирую седьмую переменную, p-значение снизится до 0,03…» Большинство исследований носит двусмысленный характер из-за путаницы в переменных и использования множественных способов интерпретации данных. Что вы предпочтете: метод, делающий ваши результаты незначимыми, или тот, который даст p-значение ниже 0,05?
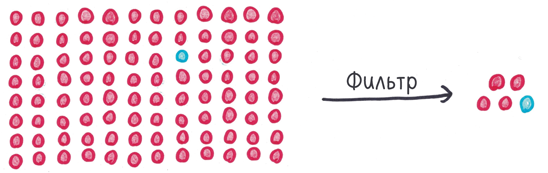
Выловить такого рода чепуху несложно. На сайте Spurious Correlations («Подложные взаимосвязи») Тайлер Виген прочесывает тысячи переменных, чтобы найти пары с тесной, но случайной корреляцией. Например, число утонувших в бассейнах с 1999 по 2009 год шокирующим образом соотносится с количеством фильмов, в которых играет Николас Кейдж.
Засорите фильтр, отсеивающий фантомы, и несколько ложноположительных результатов непременно прокрадутся в цитадель.
Я решил убедиться в этом самостоятельно и разбил 90 респондентов на три группы. Каждый испытуемый выпил или воду из-под крана, или бутилированную воду, или их смесь. Затем я измерил четыре переменные: время бега на стометровку, уровень IQ, рост и любовь к песням Бейонсе. Дальше я провел всевозможные сравнения. Кто пробегает стометровку быстрее: те, кто пил воду из-под крана, или те, кто пил бутилированную воду? Кто больший фанат Бейонсе: те, кто пил бутилированную воду, или те, кто пил смесь? И так далее. Это исследование заняло у меня восемь месяцев.
Да нет, конечно. Я заполнил таблицу с помощью генератора случайных чисел и проделал 50 экспериментов за несколько минут.
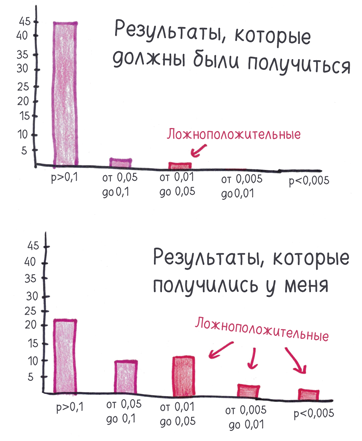
Все «респонденты» в принципе не отличались друг от друга: одна и та же программа выдавала произвольные наборы чисел. Все отличия были чисто случайными. Тем не менее три группы и четыре переменные дали 18 «значимых» результатов в 50 экспериментах.
Фантомы, которые впустило p-значение, составили не 1/20, а больше трети.
Есть и другие способы взломать p-значение. В 2011 году анонимный опрос психологов показал, что они практикуют «сомнительные исследовательские методы».
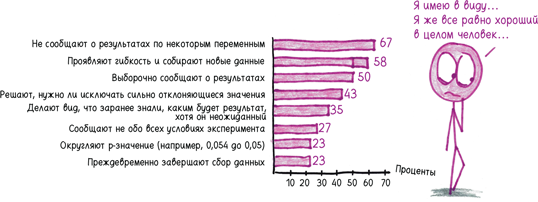
Даже самые невинно выглядящие из этих собак могут укусить. Например, сбор дополнительных данных в том случае, если вы не добились желаемого результата с первого раза. Звучит безобидно, правда?
Чтобы оценить силу этого хакерского p-взлома, я смоделировал на компьютере исследование «Кто лучше играет в орлянку?». Проще простого: два «человека» (читай: столбцы чисел) подбрасывают десять монет. Затем мы проверяем, у кого больше решек. Проведя 20 экспериментов, я добился значимого результата один-единственный раз. Вы ожидаете от p-значения именно этого: 20 попыток, один фантом. Сердце бьется ровно.
Затем я пустился во все тяжкие. Подбросьте еще одну монету. И еще одну. И еще одну. Остановите исследование, если p-значение опустится ниже 0,05 (или мы безуспешно подбросим тысячу монет).
Результат преобразился. На сей раз 12 из 20 экспериментов дали значимый результат.
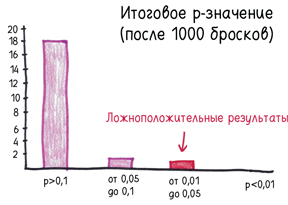
Такие фокусы не вполне научны, но это и не бесстыдное мошенничество. Три автора назвали такого рода методы в своей статье «стероидными препаратами научных исследований, которые искусственно повышают эффективность и порождают что-то вроде гонки вооружений, в которой добросовестные исследователи, соблюдающие правила, находятся в невыгодной позиции».
Есть ли способ выровнять игру?
4. Война с фантомами
Кризис, связанный с тиражированием фантомов, оживил старое соперничество между двумя бандами статистиков: частотниками и байесовцами.
Со времен Фишера приверженцы частотной вероятности имели превосходство. Их статистические модели основаны на нейтральности и минимализме. Долой субъективные суждения. Долой тенденциозность. При подсчете p-критерия нам плевать, какую гипотезу мы проверяем — безумную или надежную. Время субъективного анализа наступит позже.
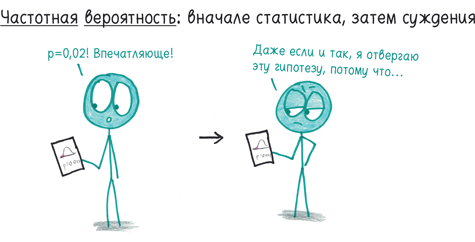
Байесовцы отвергли эту беспристрастность. Почему специалисты по статистике должны притворяться, что не видят различий между правдоподобными и абсурдными гипотезами, как будто все 0,05 созданы равными?
Байесовская альтернатива работает примерно следующим образом. Вы начинаете с предварительной оценки вероятности того, что ваша гипотеза верна. Мятные леденцы устраняют неприятный запах изо рта? Очень даже может быть. Мятные леденцы лечат кости? Крайне маловероятно. Вы формулируете эту оценку на математическом языке с помощью так называемой формулы Байеса. Затем, по итогам эксперимента, статистика поможет обновить предварительное суждение, сопоставляя прежние знания и новые данные.
Байесовцам безразлично, пользуемся ли мы условным фильтром фантомов, чтобы отсеять ложные результаты. Они заботятся о том, позволяют ли новые данные поколебать наши предварительные оценки.

Байесовцы чувствуют, что пробил их час. Они утверждают: режим приверженцев частотной вероятности потерпел крах и пришло время провозгласить новую эру. Поклонники частотной вероятности парируют: предварительные суждения слишком произвольны, чересчур уязвимы, дают широкие возможности для злоупотреблений. Они предлагают свои собственные реформы, например снижение порога p-значения от 0,05 (т.е. 1 из 20) до 0,005 (т.е. 1 из 200).
Пока специалисты по статистике предаются размышлениям, наука не стоит на месте. Исследователи в области психологии начали медленный, сложный процесс борьбы с хакерскими взломами p-значения. Они составили манифест реформ во имя прозрачности: предварительная регистрация исследований; перечисление всех измеренных переменных; регламент, заранее предписывающий, когда прекращать сбор данных и в каких случаях исключать значения, которые резко выделяются на общем фоне. Все это означает: если ложноположительные результаты проскочили фильтр p-значения ниже 0,05, вы можете заглянуть в статью и ознакомиться с результатами 19 предыдущих неудачных попыток. Один эксперт сказал мне, что эти реформы существенно важнее, чем вопросы математической философии.
Между прочим, моя дипломная работа отвечает большинству из этих стандартов. Я перечислил все собранные переменные, не исключал резко выделяющиеся результаты и разъяснил, что анализ носит предварительный характер. Тем не менее, когда я показал эту главу Кристине, она заметила: «Забавно читать в 2018 году диплом десятилетней давности. Сегодня все мои студенты предварительно фиксируют свои гипотезы, размеры выборки и т.д. Насколько же мы выросли и как многому мы научились!»
Все это должно замедлить поток варваров, прорывающихся сквозь ворота. Однако еще остается проблема с теми варварами, что засели внутри цитадели науки. Есть всего один способ выявить их: повторные исследования.
Представьте, что тысяча человек предсказывают, как выпадут десять монет. Скорее всего, одна из догадок окажется верной. Но, прежде чем вы начнете щелкать селфи с новоиспеченным другом-экстрасенсом, нужно повторить эксперимент. Попросите его снова (и, возможно, еще пару раз) предсказать, как выпадут десять монет. Настоящий экстрасенс выдержит это испытание. Тот, кому просто повезло, сядет в лужу.
То же самое относится ко всем положительным результатам. Если вывод верен, повтор эксперимента в принципе должен привести к тому же выводу. Если вывод ложен, он рассеется, как мираж.
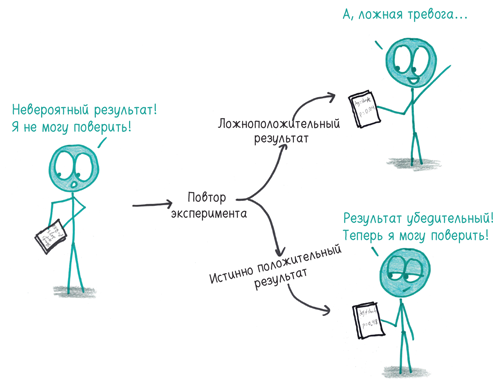
Повтор экспериментов — медленная и неблагодарная работа. Она требует времени и денег, но не ведет к сенсационным открытиям. Однако психологи понимают, что поставлено на карту, и начинают изгонять своих демонов. В 2015 году были опубликованы результаты нашумевшего проекта по тщательному повтору экспериментов ста психологических исследований. Новостные заголовки запестрели информацией о том, что выводы 61 из них не подтвердились.
Мне кажется, что эта мрачная новость свидетельствует о прогрессе. Сообщество исследователей трезво вглядывается в зеркало и признает правду, какой бы ужасной она ни была. Теперь социальные психологи надеются, что представители других наук, например медики, последуют их примеру.
Наука никогда не утверждала свою непогрешимость или сверхчеловеческое совершенство. Всегда речь шла о здоровом скептицизме, проверке всех гипотез. В этой борьбе статистика — сильный союзник. Да, она позволяет ученым вырваться на передовую, но также помогает в случае необходимости отступить назад.

