Почему нельзя доверять статистике?
И зачем ею все-таки пользоваться?
Окей, давайте взглянем непредвзято. Статистика — это ложь. Ей нельзя доверять. Так говорили все умнейшие люди в истории. Или нет?
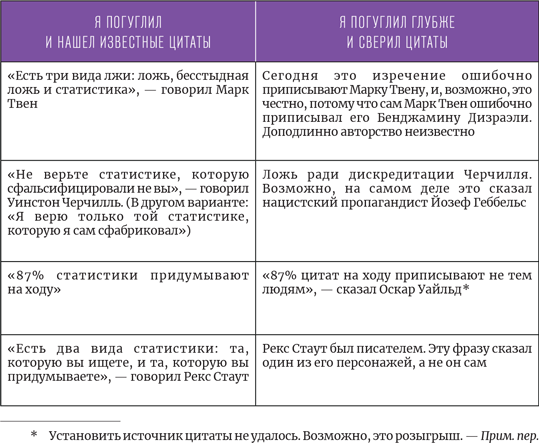

К чему я клоню? Да, цифры могут лгать. Но и слова тоже — не говоря уже о картинах, жестах, хип-хоп-мюзиклах и электронных рассылках с просьбами о фандрайзинге. Наша система морали обвиняет обманщика, а не средство обмана. На мой взгляд, самые интересные критические высказывания в адрес статистики касаются не подлости статистиков, а самой математики. Мы можем повысить ценность статистики, понимая ее несовершенства, осознавая, какую цель преследует тот или иной статистический анализ — и что он намеренно оставляет за скобками. Может быть, тогда мы сможем стать ответственными гражданами, о которых мечтал Герберт Уэллс.
1. Среднее арифметическое

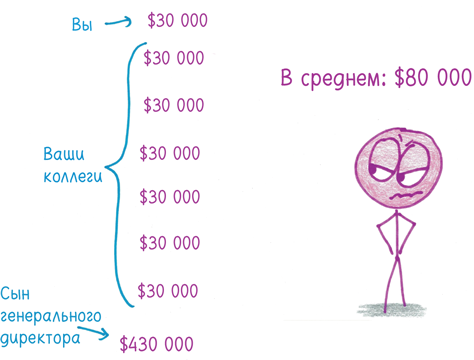
Как вычислить? Сложите все величины, которые у вас есть. Затем разделите эту сумму на количество величин.
Когда использовать? Среднее арифметическое (или среднее значение, как часто говорят) удовлетворяет основной потребности статистики: уловить центральную тенденцию совокупности величин. Каков средний рост игрока баскетбольной команды? Сколько рожков мороженого вы продаете в день? Насколько весь класс справился с контрольной работой? Если вы хотите охарактеризовать совокупность величин одним числом, то разумно в первую очередь начать со среднего арифметического.
Почему нельзя доверять? Среднее арифметическое учитывает лишь два показателя: общую сумму и количество людей, внесших свою лепту.
Если вы когда-нибудь делили пиратский клад, то осознаете опасность: есть много способов делить добычу. Сколько получает каждый? Что мы видим: баланс или перевес в чью-то пользу? Если я умял всю пиццу и ничего вам не оставил, насколько честно говорить, что в среднем мы съели по полпиццы? Вы можете сказать гостям за ужином, что у среднестатистического человека один яичник и одно яичко, но следом, возможно, повиснет неловкая пауза. (Я пробовал; так и произошло.)
Людей волнуют вопросы распределения ресурсов. Вычисляя среднее арифметическое, мы закрываем на них глаза.
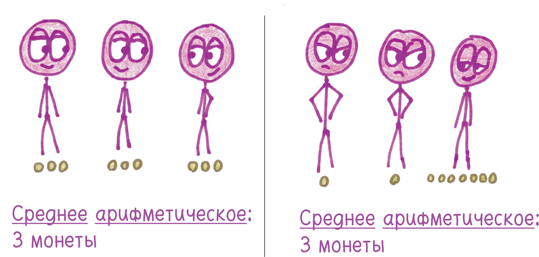
Спасительная благодать заключается в том, что эта особенность упрощает вычисления. Скажем, вы сдали экзамены на 87, 88 и 96 баллов. (Да, вы царь горы в этом классе.) Чему равен ваш средний балл? Не перегревайте нейроны сложением и делением; просто перегруппируйте величины. Отнимите шесть баллов от последней оценки; прибавьте три балла к первой и два — ко второй. Теперь ваши оценки равны 90, 90, 90 плюс один дополнительный балл. Поделите этот балл на три, и, не перенапрягая извилины, вычислите свою среднюю оценку: 90⅓.
2. Медиана


Как вычислить? Упорядочите ваши величины по возрастанию и возьмите средний элемент. Ровно половина величин будет меньше, ровно половина — больше.
Когда использовать? Медиана, как и среднее арифметическое, характеризует центральную тенденцию совокупности величин. Разница в ее чувствительности к отклонениям — или скорее нечувствительности.
Возьмем, к примеру, семейный заработок. В США богатая семья может зарабатывать в десятки (даже в сотни) раз больше, чем бедная. Вычисляя среднее арифметическое, мы исходим из того, что каждой семье достается равная доля совокупных доходов, и впадаем в искушение закрыть глаза на разброс величин и оказаться далеко от основного объема значений. В среднем семейный доход в США составляет около $75 000.
Медиана не поддается притяжению крупных величин. Вместо этого она показывает идеальную среднюю точку, доход семьи, которая богаче половины американских семей и беднее другой половины. В США это около $58 000. В отличие от среднего арифметического, это число дает ясную картину среднестатистической семьи.
Почему нельзя доверять? Вычислив медиану, вы знаете, что половина данных больше, а половина меньше. Но насколько далеко отстоят эти точки? На толщину волоса или на длину трансконтинентального полета? Вы видите только один кусок пирога, не понимая, насколько велики или малы другие. Это может ввести в заблуждение.

Когда венчурный капиталист инвестирует в новые фирмы, он исходит из того, что по большей части все они прогорят. Одно попадание в яблочко из десяти компенсирует все мелкие потери. Но медиана не учитывает эту динамику. «Типичный исход отрицательный, — вопит она. — Отменяем миссию!»
В то же время страховая компания тщательно наполняет портфель, зная, что стихийное бедствие с вероятностью 1 к 1000 сведет на нет всю скромную прибыль, накопленную за годы. Но медиана не учитывает потенциальную опасность. «Эй, типичный результат положительный, — подбадривает она. — Полный вперед!»
Вот почему вместе со средним арифметическим часто указывают медиану. Медиана рапортует о типичной величине; среднее арифметическое — обо всей совокупности величин. Они словно два ненадежных свидетеля: по отдельности их рассказы неполны, но, выслушав их вместе, мы можем восстановить более цельную картину.
3. Мода
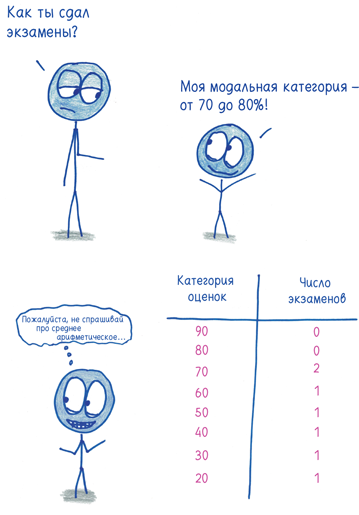
Как вычислить? Мода — наиболее часто встречающийся элемент, самый стильный, самый популярный во всем наборе данных. Как быть, если все элементы различны? В этом случае вы можете сгруппировать данные по категориям и назвать самую частую из них «модальной категорией».
Когда использовать? Этот метод используют в социологических опросах и анализе нечисловых данных. Если вы хотите узнать любимый цвет людей, вы не сможете «сложить и поделить» их, чтобы вычислить среднее арифметическое. Или, допустим, вы проводите выборы; граждане сойдут с ума, если вы упорядочите голоса от наиболее либеральных к наиболее консервативным и присудите победу кандидату, за которого отдан медианный бюллетень.
Почему нельзя доверять? Медиана не учитывает суммарное значение. Среднее арифметическое не учитывает, как оно распределено. А мода? Ну, она игнорирует и суммарное значение, и то, как оно распределено, и почти все прочее.
Наиболее распространенное не означает показательное. Модальная зарплата в Соединенных Штатах равна нулю — не потому, что большинство американцев безработные и нищие, а потому, что зарплаты наемных работников разбросаны по всему спектру от одного доллара до $100 млн, в то время как все безработные получают одинаково — ноль. Этот статистический показатель никак не характеризует США. Так обстоят дела почти во всех странах, в этом особенность капитализма.
Метод модальной категории лишь частично устраняет проблему. Он дает ошеломляющую власть человеку, который сообщает данные: он может ловко перекроить границы категорий в соответствии со своей повесткой дня. В зависимости от того, какие интервалы я выберу, можно утверждать, что модальная американская семья зарабатывает от $10 000 до $20 000 (если взять интервалы размером 10 000), или от $20 000 до $40 000 (интервалы по $20 000), или от $38 000 до $92 000 (если идти по ступеням налоговой шкалы). Один и тот же набор данных, один и тот же метод. И все же портрет полностью преображается — все зависит от рамки, которую выбрал художник.
4. Перцентиль

Как вычислить? Напоминаю, что медиана находится ровно посередине упорядоченного ряда данных. А перцентиль — это медиана с регулятором. 50-й перцентиль — это сама медиана (половина величин больше, половина меньше). Но вы можете выбрать и другие перцентили. 90-й перцентиль на самой верхотуре: всего лишь 10% величин больше, а 90% величин меньше. В свою очередь, 3-й перцентиль почти на дне: 3% величин меньше, 97% больше.
Когда использовать? Метод перцентилей удобный и гибкий, он идеально подходит для нашего любимого времяпрепровождения — выстраивания рейтингов. Вот почему стандартные тесты часто дают оценки в перцентилях. Сырые данные не слишком информативны. Например, «я ответил верно на 72% вопросов». Но сколько среди них головоломных и сколько легких? В то же время «я на 80-м перцентиле» в точности показывает ваш результат. Вы лучше 80% испытуемых и хуже 20%.
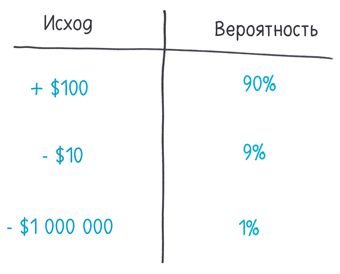
Почему нельзя доверять? У перцентилей та же ахиллесова пята, что и у медианы. Вы знаете, сколько величин больше или меньше определенного значения, но не знаете насколько. Возьмем, к примеру, финансовый сектор, где перцентили используются для оценки потерь от инвестиций. Вначале вы прикидываете разброс потенциальных результатов, от триумфа до краха, а затем выбираете перцентиль (обычно 5-й) и называете его «стоимость под риском», или VaR (Value at Risk). Он показывает наихудший сценарий. По сути дела, хуже будет ровно 5% вариантов развития событий. VaR ничего не говорит о том, насколько хуже. Он не учитывает, сколько вы потеряете в 5% случаев — несколько центов или миллиарды долларов. Возможно, вы будете лучше представлять себе пространство возможностей, если узнаете другие перцентили (например, 3-й, 1-й и 0,1-й), но этот метод по определению не показывает самые крупные и болезненные убытки, поэтому худший сценарий всегда будет оставаться вне зоны видимости.
5. Процентное изменение

Как вычислить? Прежде чем сообщить, насколько изменилась величина, поделите эту разницу на исходное значение.
Когда использовать? Процентное изменение позволяет посмотреть на вещи в перспективе. Оно определяет прибыли и убытки как части целого. Скажем, моя прибыль составила $100. Если вначале у меня было всего $200, то этот золотой дождь обеспечил рост капитала на 50%, и я прыгаю от счастья и виляю хвостом, как Снупи. Но, если у меня уже было $20 000, рост моего дохода составляет всего лишь 0,5%; я ограничиваюсь тем, что вскидываю вверх кулак. Перспектива имеет решающее значение, когда вы наблюдаете рост величины с течением времени. Если бы 70 лет назад американцы услышали, что наш ВВП за год вырос на $500 млрд, они испытали бы благоговейный трепет. Если бы они узнали, что рост составил 3%, они бы не сильно удивились.
Почему нельзя доверять? О, я всецело за взгляд в перспективе. Но процентное изменение, пытаясь обеспечить контекст, может его, наоборот, уничтожить. Когда я жил в Великобритании, вкусный томатный соус по два фунта за банку иногда продавался со скидкой — в два раза дешевле. В эти дни я как будто выигрывал джекпот: 50% экономии! Я волок домой дюжину банок — можно заправлять равиоли целый месяц. Вскоре меня пригласили на свадьбу в США. За неделю авиабилеты могли подскочить в цене на 5%. «Ну и ладно, — сказал я, соглашаясь на повышенную цену. — Это ненамного больше».

Вы понимаете проблему: из-за инстинктов у меня оказалось на пенни ума и на фунт глупости. «Огромная» скидка сэкономила мне 12 фунтов, в то время как «незначительный» рост цен на авиабилеты стоил мне 30 фунтов. Деньги есть деньги, будь то счет в овощной лавке на $20 или ипотека в $200 000. Большие процентные скидки на дешевые товары — ерунда на фоне нескольких процентов подорожания дорогих вещей.
6. Диапазон
Как вычислить? Диапазон — это разница между наибольшей и наименьшей величиной.
Когда использовать? Среднее арифметическое, медиана и мода имеют дело с основной тенденцией: они сводят все разнообразие набора данных до одного репрезентативного значения. Диапазон преследует противоположную цель: не замести разногласия под ковер, а вычислить и показать их, чтобы измерить разброс данных. Заслуга диапазона в его простоте. Мы воспринимаем набор данных как спектр от наименьшего к наибольшему и выясняем ширину этого спектра. Это быстрая и грубая оценка разнообразия.
Почему нельзя доверять? Диапазон учитывает только два куска пирога — наименьший и наибольший. Мы упускаем очень много важной информации, а именно размеры всех прочих кусков. Они близки к максимуму? Близки к минимуму? Распределены равномерно? Диапазон не знает и не хочет выяснять. Чем больше набор данных, тем сомнительнее становится смысл диапазона, потому что он игнорирует миллионы промежуточных значений, чтобы узнать о двух наибольших отклонениях. Узнай инопланетянин о двухметровом диапазоне роста взрослых людей (от рекордно низких 60-сантиметровых до рекордно высоких — 274 см), он был бы крайне разочарован, посетив Землю и выяснив, что все мы уныло средние — примерно от 152 до 183 см.
7. Дисперсия (и среднеквадратичное отклонение)
Как вычислить? Среднеквадратичное отклонение показывает, грубо говоря, насколько далеко типичная величина из набора данных отстоит от среднего арифметического.
Если вы хотите приготовить дисперсию у себя на кухне, воспользуйтесь следующим рецептом: (1) найдите среднее арифметическое вашего набора данных; (2) вычислите, насколько далеко каждая величина отстоит от среднего арифметического; (3) возведите эти разности в квадрат; (4) найдите среднее арифметическое квадратов разностей. Среднее арифметическое квадратов отклонений от среднего арифметического и есть дисперсия.
Если вы извлечете квадратный корень из дисперсии, вы получите «среднеквадратичное отклонение». Это более естественная величина, поскольку дисперсия измеряется в странных единицах. (Что такое «доллар в квадрате»? Никому это не ведомо.)
Дисперсия и среднеквадратичное отклонение идут вместе рука об руку, поэтому мы обсуждаем их в одном параграфе.
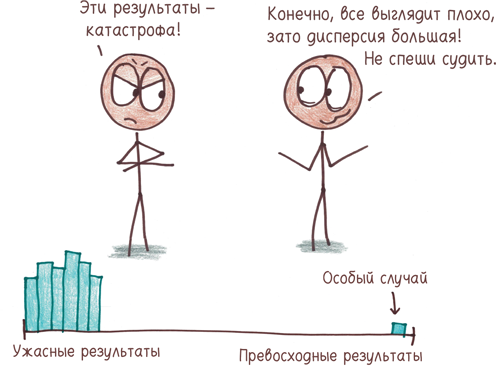
Когда использовать? Как и диапазон, дисперсия и среднеквадратичное отклонение дают численное значение разброса величин в наборе данных, но (говорю со всей беспристрастностью любящего отца) они лучше. Диапазон — быстрая, сделанная на скорую руку оценка разброса; дисперсия — несущая опора статистики. Дисперсия учитывает вклад каждой величины из набора данных и достигает сложности симфонии, в то время как диапазон бренчит на двух струнах.
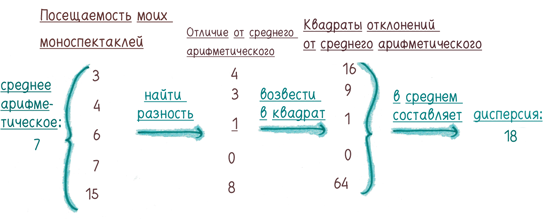
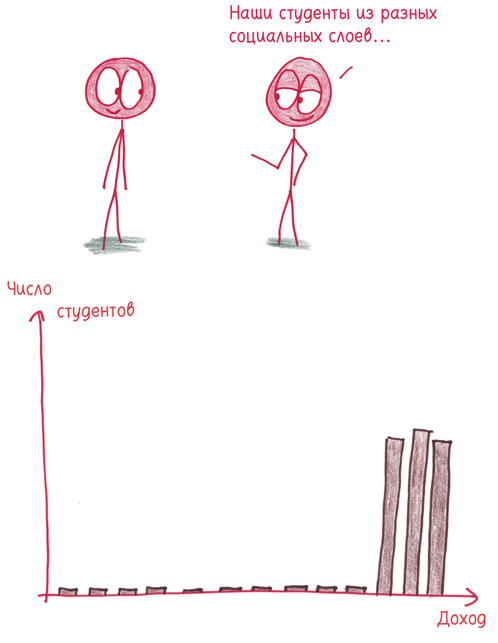
Логика дисперсии, пускай витиеватая, при ближайшем рассмотрении имеет смысл. Ключевую роль играет отличие от среднего арифметического. Большая дисперсия означает, что данные широко разбросаны; маленькая дисперсия означает, что они тесно жмутся друг к другу.
Почему нельзя доверять? Разумеется, дисперсия учитывает вклад каждой величины из набора данных. Но вы не можете сказать, кто вносит что.
Точнее говоря, одна далеко отстоящая величина может обеспечить взрывной рост дисперсии. Из-за возведения в квадрат одно значительное отклонение от среднего арифметического (например, 122 = 144) может внести больший вклад, чем дюжина небольших (например, 32 = 9; двенадцать девяток дают всего-навсего 108).
У дисперсии есть еще одна особенность, которая многих ставит в тупик. (Она не плохая, просто парадоксальная.) Студенты склонны называть набор данных с большим разнообразием величин (например, 1, 2, 3, 4, 5, 6) более «рассредоточенным», чем набор данных с повторяющимися величинами (например, 1, 1, 1, 6, 6, 6). Но дисперсия не заинтересована в «разнообразии»; ее интересует только отклонение от среднего арифметического.
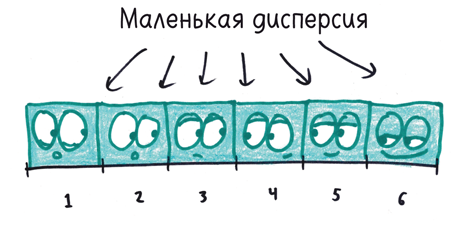
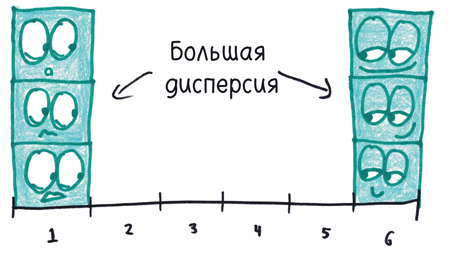
С точки зрения дисперсии разброс второго набора данных (с повторяющимися величинами, отстоящими далеко от среднего арифметического) перевешивает разброс первого набора (где значения не повторяются, но в основном ближе к среднему).
8. Коэффициент корреляции

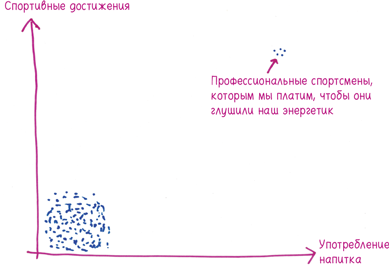
Как вычислить? Корреляция показывает взаимосвязь между двумя переменными. Например, рост и вес человека. Или цена марки автомобиля и объем продаж. Или бюджет фильма и кассовые сборы.
Шкала идет следующим образом: от максимума на 1 («ого, они всегда идут вместе») к середине на 0 («м-да, никакой взаимосвязи») и, наконец, до минимума на –1 («хм, одно исключает другое»).
Однако это очень поверхностный обзор. Как коэффициент корреляции работает на самом деле, рассказано в примечании.
Когда использовать? Жители богатых стран счастливее? Решетки на окнах предотвращают преступления? Распитие красного вина продлевает жизнь или просто растягивает вечеринки? Отвечая на все эти вопросы, мы пытаемся выяснить связь между парой переменных, между предполагаемой причиной и следствием. В идеале вы ставите эксперимент и находите ответ. Ежедневно наливайте ста людям красное вино, а другим ста людям — виноградный сок и посмотрите, кто проживет дольше. Однако такое исследование медленное, дорогое и зачастую неэтичное. Можно только посочувствовать беднягам, приговоренным к сухому закону.
Корреляция позволяет ответить на тот же вопрос косвенным образом. Выберите группу людей, измерьте, сколько вина они пьют, узнайте их возраст и посмотрите, живут ли винопийцы дольше. Разумеется, даже сильная корреляция не означает причинно-следственной связи. Может быть, вино продлевает жизнь. Может быть, длинная жизнь побуждает людей пить алкоголь. Может быть, оба фактора вызваны третьей переменной (например, богатые люди живут дольше и могут позволить себе покупать вино). Узнать невозможно.
Даже с учетом этого недостатка изучение коэффициента корреляции — прекрасное начало исследований. Эта методика дешевая, быстрая и позволяет обрабатывать большие массивы данных. Она не может выявить причины точно, но может предложить интригующие гипотезы.
Почему нельзя доверять? Коэффициент корреляции — одна из самых агрессивных статистических величин. Она перемалывает сотни или тысячи пар переменных в одно число от –1 до 1. Неудивительно, что некоторые вещи остаются за бортом. Проиллюстрируем этот факт математическим парадоксом, известным под названием квартет Энскомба.
Переступим порог Энскомбской Академии чародейства и волшебства, где ученики неделями готовятся к экзаменам по четырем дисциплинам: зельеварение, трансфигурация, заклинания и защита от темных искусств. Мы будем учитывать две переменных: оценку ученика (от 0 до 13) на каждом экзамене и количество часов на подготовку к нему.
Глядя на обзорную статистику, вы можете подумать, что результаты по четырем экзаменам одни и те же:
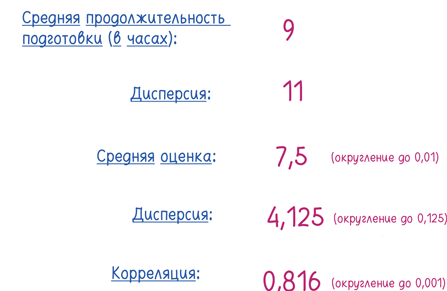
И все же… ну, просто присмотримся. (Каждая точка обозначает ученика.)
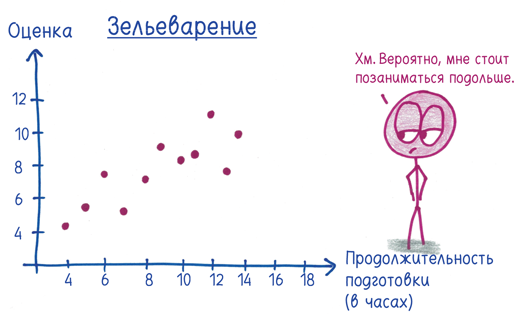
Экзамен по зельеварению соответствует моему стереотипу сдачи экзаменов. Длительная подготовка, скорее всего, повысит ваши результаты, но вовсе не обязательно. Вмешивается случайный шум. Таким образом, корреляция равна 0,816.
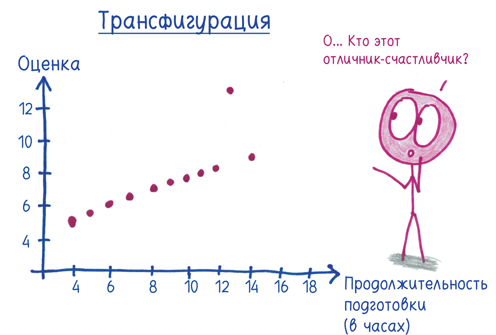
В то же время оценки по трансфигурации лежат на почти идеальной прямой: каждый дополнительный час подготовки приносит дополнительные 0,35 балла, за исключением одного выдающегося ребенка, который снижает корреляцию от идеальной единицы до 0,816.
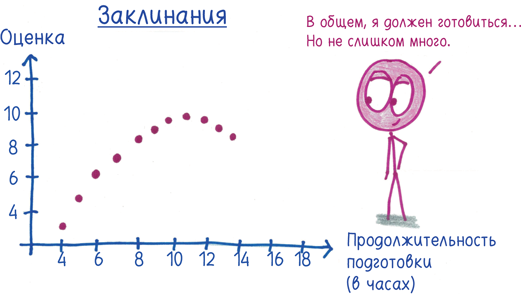
Экзамен по заклинаниям соответствует еще более четкой схеме: чем больше вы готовитесь, тем лучше ваша оценка, но в какой-то момент тенденция меняется. Если вы будете заниматься дольше десяти часов, с каждым часом ваша оценка будет ухудшаться (возможно, из-за сонливости). Как бы то ни было, корреляция может выявить только линейную зависимость, поэтому она не замечает эту параболу и коэффициент корреляции равен 0,816.
Наконец, перед экзаменом по защите от темных искусств все ученики занимались по 8 часов, но получили разные оценки. Зная продолжительность подготовки, вы не можете предсказать оценку. Есть одно исключение: трудоголик-одиночка потратил 19 часов на подготовку и получил высший балл. Одна-единственная точка повышает коэффициент корреляции от 0 до… 0,816.
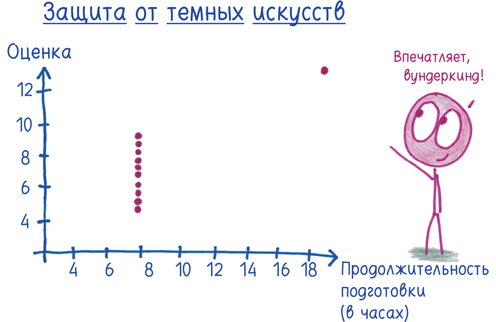
Оценки по каждому экзамену следуют своей логике, подчиняются уникальной схеме. Но коэффициент корреляции упускает это из виду.
Опять-таки такова природа статистики. Как я люблю говорить:
Статистика — ненадежный свидетель.
Она не лжет, но никогда не говорит всю правду.
Цитируйте меня на здоровье. Или, следуя традиции, придумайте афоризм о статистике самостоятельно и припишите его мне.

