Атомы состоят из электронов, вращающихся вокруг атомных ядер. Атомные ядра, как я уже рассказывал, состоят из протонов и нейтронов. Простейшим случаем, с рассмотрения которого мы и начнём, является атом водорода, состоящий из одного электрона, вращающегося вокруг ядра, состоящего из одного протона. Размер атома водорода имеет порядок 10⁻¹⁰ метра. Единицу измерения 10⁻¹⁰ метра называют также ангстремом. Говоря, что один ангстрем равен 10⁻¹⁰ метра, мы имеем в виду, что в одном метре 10¹⁰, или десять миллиардов, ангстрем. Размер атомного ядра примерно в сто тысяч раз меньше. Смысл утверждения, что размер атома имеет порядок одного ангстрема, состоит в том, что электрон крайне редко удаляется от ядра на расстояние больше одного ангстрема. Неопределённость положения электрона — Δx — также порядка одного ангстрема, поэтому невозможно сказать, с какой стороны от ядра в конкретный момент времени находится электрон. Принцип неопределённости требует, чтобы неопределённость импульса электрона — Δp — удовлетворяла неравенству Δp × Δx ≥ h/4π. Это приводит к тому, что электрон в атоме водорода должен обладать некоторой средней скоростью, порядка одной сотой скорости света, но направление этой скорости в каждый конкретный момент времени принципиально неопределённо. Неопределённость импульса электрона является, в сущности неопределённостью самого импульса, поскольку не определено его направление. Общая картина выглядит так, что электрон пойман в ловушку кулоновским притяжением ядра, но квантовая механика запрещает ему находиться в этой ловушке в состоянии покоя. Вместо этого он непрерывно «блуждает» в переделах ловушки, и характер его блуждания описывается математическим аппаратом квантовой механики. Область блуждания электрона и определяет размер атома. Если бы электрону разрешили спокойно сидеть на одном месте, он бы сразу упал на ядро под действием кулоновской силы притяжения. В результате все материальные предметы сжались бы до ядерной плотности, что было бы весьма некомфортно. Таким образом, квантовый запрет на неподвижность электронов внутри атомов является большим благом для нас.

Несмотря на то что электрон в атоме водорода обладает неопределённой координатой и неопределённым импульсом, его энергия вполне определённа. На самом деле электрон может обладать несколькими возможными дискретными значениями энергии. О такой ситуации физики говорят, что энергия электрона в атоме «квантована». Это значит, что электрон имеет выбор из некоторого определённого набора вариантов. Чтобы лучше разобраться в этом странном положении дел, вернёмся к уже знакомой нам кинетической энергии. Мы помним, что кинетическая энергия определяется формулой K = ½mv². Для начала применим эту формулу к автомобилю. Меняя силу нажатия на педаль газа, вы можете придать автомобилю любую скорость в пределах его технических возможностей. Однако если бы энергия автомобиля квантовалась, то при условии, что масса автомобиля неизменна, вы могли бы заставить его двигаться только с какой-либо фиксированной скоростью из дискретного набора, например только со скоростью 10, 15 или 25 километров в час, но не 11, 12 или 12,5 километра в час.

Квантование энергии электрона в атоме водорода возвращает меня к аналогии с музыкой. Я уже говорил о подобной аналогии на примере полиритмии 4:3 в «Экспромт-фантазии». Устойчивый музыкальный ритм характеризуется определённой частотой. Каждый квантовый энергетический уровень атома водорода также соответствует определённой частоте. Электрон может «выбрать» один из этих уровней, подобно тому как музыкант может выбрать какой-то определённый ритм и выставить его на метрономе. Но электрон может также частично находиться на одном энергетическом уровне, а частично на другом. Это явление носит название «суперпозиция». Ритм «Экспромт-фантазии» как раз является суперпозицией двух различных ритмов, исполняемых правой и левой рукой.

Итак, как я сказал, электрон в атоме обладает квантово-механически неопределёнными координатой и импульсом, но может иметь определённую энергию из дискретного набора. Не кажется ли вам странным, что энергия имеет фиксированное определённое значение, в то время как координаты и импульсы неопределённы? Чтобы понять, как такое может быть, давайте отвлечёмся на ещё одну музыкальную аналогию. Представьте себе фортепианную струну. После удара молоточка струна начинает вибрировать с определённой частотой, или тоном. Например, струна, отвечающая за ноту «ля» первой октавы, вибрирует с частотой 440 раз в секунду. Физики измеряют частоту в герцах (сокращённое обозначение — Гц); один герц соответствует одному колебанию в секунду. Таким образом, нота «ля» первой октавы звучит с частотой 440 Гц. Это гораздо быстрее, чем ритм «Экспромт-фантазии», где, как вы помните, правая рука извлекает из рояля примерно 12 нот в секунду, то есть с частотой 12 Гц. Но это гораздо меньше частоты колебаний электрона в атоме водорода. На самом деле поведение струны гораздо сложнее простого колебания. Помимо основной частоты струна выдаёт множество обертонов на более высоких частотах, и именно эти обертоны придают звучанию рояля характерную окраску.

Может показаться, что эта аналогия весьма далека от квантово-механического движения электрона в атоме водорода, но на самом деле оба процесса очень похожи. Минимальная возможная энергия электрона в атоме водорода сродни основной гармонике фортепианной струны: 440 Гц для ноты «ля» первой октавы. Немного упрощая, можно сказать, что частота колебаний электрона в его основном состоянии равна примерно 3×10¹⁵ Гц. Остальные энергии, доступные электрону, аналогичны обертонам фортепианной струны.

Волны на фортепианной струне и квантово-механическое движение электрона в атоме водорода являются примером так называемых стоячих волн. Стоячие волны — это колебания, которые никуда не движутся. Фортепианная струна закреплена на раме своими концами, и её колебания пленены в пределах длины струны. Квантово-механическое движение электрона также заключено в очень маленькой области — чуть меньше одного ангстрема в поперечнике. Главная идея, лежащая в основе математического аппарата квантовой механики, состоит в том, чтобы представить движение электрона в виде волны. Поскольку волна имеет вполне определённую частоту, подобную основной гармонике фортепианной струны, она имеет и вполне определённую энергию. Но положение электрона в пространстве, например его расстояние от ядра, не может быть описано конкретным числом, поскольку волна присутствует одновременно повсюду внутри атома, точно так же как колебания фортепианной струны происходят одновременно по всей её длине. Всё, что мы можем сказать об электроне, — это лишь то, что он почти всегда находится где-то в пределах одного ангстрема от ядра.

Узнав, что электроны описываются в виде волн, вы вправе спросить: «В виде волн чего?». Это сложный вопрос. Одни считают, что этот вопрос не имеет смысла, другие — что существует некое «электронное поле», пронизывающее всё пространство-время, а электроны представляют собой возбуждения этого поля. Электронное поле аналогично фортепианной струне, а электроны — возникающим на ней колебаниям.

Волны не всегда заперты в маленькой области пространства типа внутренности атома. Например, морские волны путешествуют многие километры, прежде чем разбиться о прибрежные скалы. Примером путешествующих квантово-механических волн являются, в частности, фотоны. Но перед тем как мы углубимся в изучение фотонов, я должен остановиться на одной формальности, имеющей отношение к вещам, которые мы будем обсуждать в последующих главах. Говоря о частоте основного состояния электрона в атоме водорода, я упомянул о том, что это упрощённое описание. Чтобы пояснить, что именно упрощено, я напишу ещё одну формулу: E = hv, где E — это энергия, v — частота, а h — та самая постоянная Планка, которая уже появлялась ранее в формулировке принципа неопределённости. E = hv — замечательная формула, она объясняет нам, что, в сущности, представляет собой частота: это просто энергия в новом облике. Но вот беда: существуют различные виды энергии. Электрон обладает энергией покоя. Он также обладает кинетической энергией. И вдобавок он обладает энергией связи, необходимой для того, чтобы освободить электрон из атома. Какую из этих энергий следует использовать в формуле E = hv? Когда я говорил, что частота основного состояния электрона равна 3×10¹⁵ колебаний в секунду, я имел в виду кинетическую энергию плюс энергию связи, исключая энергию покоя. Но это весьма произвольное допущение. Я мог бы включить в общую энергию и энергию покоя, если бы почувствовал, что это необходимо. Это означает, что частота в квантовой механике имеет некоторую недоопределённость, а это выглядит нехорошо.

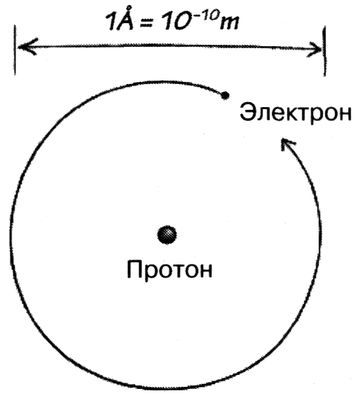
Классическое представление об атоме водорода: электрон обращается по орбите вокруг протона

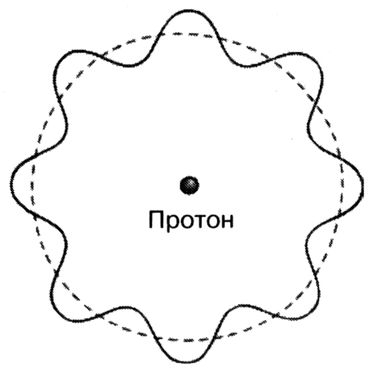
Квантово-механическое представление электрона в виде стоячей волны. Волна не имеет определённого положения на орбите, но обладает определённой энергией и частотой

Вот как можно разрешить указанную трудность. Давайте зададимся вопросом: «Что происходит, когда электрон переходит с одного энергетического уровня на другой?». Если электрон перескакивает на более низкий энергетический уровень, он освобождается от избытка энергии путём испускания фотона. Энергия фотона равна разности энергий двух уровней: того, с которого электрон перескакивает, и того, на которой он перескакивает. Теперь неважно, учитываем мы энергию покоя электрона или нет, потому что нас интересует только разность между двумя энергетическими уровнями, в то время как энергия покоя электрона не изменяется и не входит в окончательный результат. Правильным использованием формулы E = hv будет приравнять E к энергии фотона. Тогда v будет означать частоту фотона, имеющую вполне определённое значение, уже без всяких неоднозначностей. Остаётся ответить на последний вопрос: «Что же означает частота фотона?». Этим мы сейчас и займёмся.