Если вы находитесь в ситуации А, а хотите быть в ситуации Я, вы, должно быть, уже знаете правило вроде «если А – действуй (какое-то действие) – то Я». В этом случае достаточно просто совершить действие – и вы достигнете вашей цели. Но что, если вы не знаете подобного правила? Тогда вы можете попытаться найти в своей памяти цепочку из двух правил, которые помогут вам достичь цели через промежуточную ситуацию М.

Но что, если ваша проблема не может быть решена двумя такими шагами? Тогда вам придется рассчитывать ситуацию еще на несколько шагов вперед – и если каждый шаг предлагает два варианта или большее их количество, тогда масштаб поисков будет расти экспоненциально, как дерево со множеством ветвей. Например, если для решения нужно совершить двадцать шагов, вам придется искать вариант среди более чем миллиона попыток.

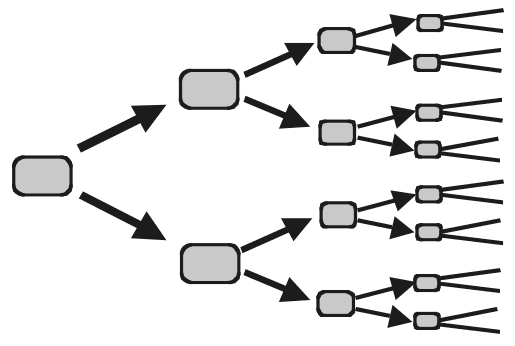
К счастью, существует стратегия, которая в некоторых случаях может резко уменьшить масштаб этих поисков – потому что, если действительно существует путь из двадцати шагов от А до Я, значит, должно существовать промежуточное место в десяти шагах от каждой точки. И если вы начнете искать с обоих концов, они должны встретиться в промежуточной точке М посередине, и тогда с каждой стороны ваших поисков будет всего около тысячи развилок!

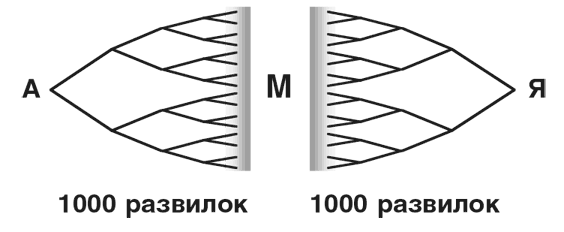
Это означает, что вам понадобится всего две тысячи попыток – это в несколько сот раз меньше, чем двадцатиступенчатый поиск! Подозреваю, что все используют подобный трюк – одновременно глядя вперед и назад, – причем даже не подозревают об этом.

Но подождите, это еще не все. Представьте, что у вас получится каким-то способом угадать, где может находиться промежуточное место М. Тогда вы сможете разделить каждое десятиступенчатое дерево на пару пятиступенчатых. Если это сработает, ваш окончательный поиск окажется почти в десять тысяч раз меньшим по объему, чем изначальный!

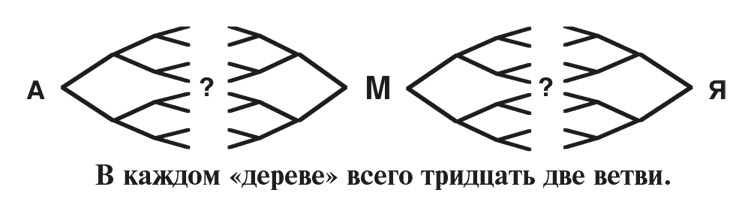
Но что, если ваша догадка окажется неверной, потому что пути от А до Я через М не существует? Тогда вы сможете сделать предположение о другой М – и даже если не добьетесь успеха в течение первых сорока девяти экспериментов, то все равно проделаете меньшую работу, чем если бы воспользовались изначальным вариантом поиска. Так что, прежде чем начинать масштабный поиск, возможно, стоит потратить время на анализ, чтобы попытаться найти несколько «островков» или «опорных пунктов». Потому что, если вы преуспеете, вам удастся заменить одну невероятно сложную задачу на несколько отдельных и значительно более простых!

В самом начале развития теории искусственного интеллекта многие исследователи пытались использовать подобные трюки для уменьшения объема очень обширных поисков, но в основном им это не удавалось. Правда, в 1997 году компьютер победил действовавшего чемпиона мира по шахматам, употребив лучшую известную тогда технологию сужения поиска в «дереве ходов» шахматной игры. И все равно ему пришлось рассматривать множество миллиардов возможных позиций. В то время как лучшие шахматисты-люди, по утверждению шахматного гроссмейстера и психолога Адриана де Гроота, рассматривают перед каждым ходом в игре всего-навсего несколько десятков вариантов.

В следующих главах будет показано, что самые эффективные способы решения человеком сложных задач основаны не на масштабных поисках. Вместо этого мы полагаемся на более умные способы, привлекаем обширные пласты житейских знаний, чтобы «разделять и властвовать» над проблемами, с которыми сталкиваемся. Например, чтобы обнаружить, где могут крыться самые важные «островки», мы можем попытаться найти подцели для наших целей – а можем поискать аналогии в проблемах, которые нам доводилось решать в прошлом. Мы обсудим эти методы в главе шестой.