Книга: Космос. Иллюстрированная история астрономии и космологии
Назад: ЧЕТЫРЕ АСТРОНОМА И ЧЕТЫРЕ АСПЕКТА ИСЛАМСКОЙ АСТРОНОМИИ
Дальше: МУСУЛЬМАНСКИЕ ОБСЕРВАТОРИИ
НАСИР АД-ДИН АТ-ТУСИ И ЕГО ПОСЛЕДОВАТЕЛИ
Насир ад-Дин ат-Туси (1201–1274) был одной из тех исторических фигур, которые сочетали в себе мощный интеллект, неиссякаемую энергию и удачливость, что позволило ему добиться высокого общественного положения в одном из центров исламского региона. Это упростило признание его заслуг другими специалистами и, похоже, наделило его таким интеллектуальным влиянием, каким не обладал ни один другой средневековый астроном. Будучи рожденным в Тусе (Персия; название города стало частью его имени) на охваченном войной континенте, он сначала прошел домашнее обучение под руководством своего отца – одного из представителей долгой шиитской научной традиции, а затем получил образование в нескольких учебных заведениях, в том числе в Нишапуре – влиятельном образовательном центре. Он был хорошо подготовлен практически во всех областях исламской учености и заслуженно считал себя преемником эллинистической науки и философии. В итоге он нашел защиту и приют, поступив на службу к Исмаилитскому правителю крепости Аламут, Великому Владыке ассасинов или «Старцу гор», как его называли на Западе. Он перемещался вместе с придворными из одной горной крепости в другую, пока в 1256 г. Ильханский завоеватель Хулагу (правнук Чингисхана) не покончил с правлением Исмаилитов на севере Персии. Астрономическая известность обеспечила ему место в ближайшем окружении Хулагу. Он присутствовал при захвате Багдада в 1258 г., а годом позже склонил Хулагу-хана к тому, чтобы начать строительство обсерватории в Мараге – на северо-западе современного Ирана (восемьюдесятью километрами южнее Табриза). Брат Хулагу Мункэ, правивший на обширной территории Китая, положил начало строительству обсерватории в Пекине, однако она так и не была завершена при его жизни.
Марагинская обсерватория являлась во многих отношениях первым крупномасштабным исследовательским институтом, административная структура которого имела много общего с современной. Она обладала крупной научной библиотекой с постоянным библиотекарем, и ее штат насчитывал по меньшей мере десять астрономов; в их числе присутствовал как минимум один китайский астроном – Фао Мунцзи, но, вполне вероятно, что их было больше. В обсерватории имелось множество дорогостоящих инструментов – большой стенной квадрант, параллактические линейки, армиллярные сферы и квадранты, приспособленные для измерения азимутов. Здесь были составлены Ильханские астрономические таблицы, завершенные в 1272 г., уже при жизни наследника Хулагу – Абака-хана.
Насир ад-Дин ат-Туси написал множество весьма важных работ по логике, философии, математике и теологии. Благодаря ему удалось восстановить теоретические наработки Ибн Сины – величайшего врача и философа из Бухары, жившего двумя столетиями ранее. Ат-Туси был искусным геометром, и нет ничего удивительного в том, что он пытался использовать свои геометрические навыки для решения натурфилософских проблем, поднятых Ибн ал-Хайсамом. Составляя свои критические замечания к птолемеевой астрономии в работе «Тазкира» («Трактат по астрономии»), он ясно дает понять: это сочинение задумано как некое резюме, предназначенное для непрофессионалов, поэтому в него не входят сложные математические доказательства. В нем рассматриваются лишь внешние аспекты, касающиеся как земных, так и небесных тел. Он сопровождает свою критику Птолемея конструктивными предложениями в виде новых планетных моделей. Одно из наиболее интересных предложений такого рода вытекает из следующей теоремы:
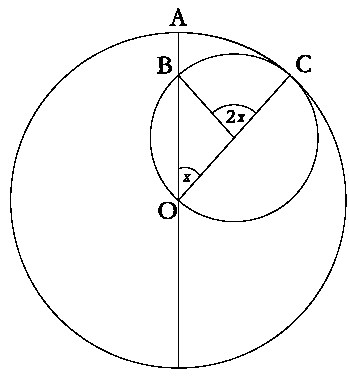
Если один круг катится по внутреннему периметру другого круга, причем радиус второго круга в два раза превосходит радиус первого, то любая из точек первого круга будет описывать прямую линию (вдоль диаметра неподвижного круга).
Такое построение, часто обозначаемое сегодня как «пара Туси», проиллюстрировано на ил. 85. Доказать эту теорему очень легко: длина линий, образуемых периметрами касающихся друг друга кругов должна быть одинаковой, и каждую из них можно определить через радиус и угол. Угол, образуемый радиусом неподвижного круга, вдвое меньше, но радиус – вдвое больше, чем у катящегося круга.
85
Пара Туси, позволяющая получать прямолинейное движение посредством одного круга, вращающегося внутри другого. Дуги BC и AC одинаковы по длине; следовательно, если меньший круг вращается без проскальзывания внутри большего, то точка B (жестко закрепленная на своем круге) в какой-то момент должна достигнуть точки A. Таким образом, эта точка всегда будет двигаться вдоль линии AO.
Образование прямой линии путем сложения двух круговых движений было, само по себе, довольно интересным результатом, но давайте обратим внимание на то, как катящийся круг (или сфера) мог быть использован для физической интерпретации птолемеевых моделей (чего в итоге и хотели добиться Ибн ал-Хайсам и его последователи). Изложение указанной теоремы в геометрическом виде – это очень хороший знак, при условии что мы отнесемся к нему с должным вниманием. Помимо самого ат-Туси, еще несколько марагинских астрономов стремились использовать его идеи для разработки корректных физических моделей, более или менее эквивалентных птолемеевым, и таким образом ответить на критику, высказываемую Ибн ал-Хайсамом, ат-Туси и прочими астрономами, разделявшими их взгляды. В их число входили коллеги ат-Туси: ал-Урди (ум. в 1266), который участвовал в строительстве обсерватории, его ученик аш-Ширази (1236–1311) и живший веком позже астроном Ибн аш-Шатир (1304–1375).
Ат-Туси обобщил свою модель на случай трех измерений. Полагая, что плоскости двух вышеупомянутых кругов наклонены друг к другу под малым углом, он обнаружил следующее: в данном случае осциллирующее движение будет образовывать дугу, очень близкую к дуге большого круга. Он использовал это остроумное построение в теории планетных долгот. Сделанное им вызывает повышенный интерес по той причине, что Коперник неоднократно выполнял в точности такие же преобразования и, кроме того, использовал многие другие положения, полученные ат-Туси и его последователями, поэтому вряд ли есть причина сомневаться в хорошем знании Коперником некоторых из вышеупомянутых текстов или других источников, где можно найти их подробный пересказ. Греческие и латинские материалы, легшие в основу построений ат-Туси, широко циркулировали в Италии, когда там учился Коперник, и своевременно будет поднять вопрос о том, кому был обязан своими открытиями молодой польский ученый.
Ответы содержатся в его поистине величайшем сочинении «De revolutionibus», хотя оно было опубликовано только в год его смерти – в 1543 г. В нем, пытаясь обосновать свою модель непостоянства скорости прецессии и изменения угла наклона эклиптики, Коперник использует приемы, которые впервые употребил ат-Туси. И в этой книге, и в более ранней работе «Малый комментарий» он применяет приемы ат-Туси для разработки собственной теории планетных долгот, объясняя с их помощью осцилляцию плоскостей планетных орбит. В «Малом комментарии» он использовал простейшую двумерную модель, чтобы получить изменения радиуса орбиты Меркурия. Ту же самую процедуру он привычно повторил и в «De revolutionibus». В «Малом комментарии» он положил в основу собственных моделей планетных долгот модели, разработанные ал-Урди и аш-Шатиром, хотя применение их к нижним планетам оказалось ошибочным, в то время как в «De Revolutionibus» его модели, кроме перечисленных, увязаны с другими моделями, разработанными ал-Урди и аш-Ширази. В обеих работах лунная модель была более или менее такой же, как у Ибн аш-Шатира, о чем мы подробнее поговорим чуть ниже.
Есть еще один пример (хотя и не бесспорный) потенциального влияния на западную ренессансную астрономию как минимум одного исламского источника, который мог иметь непосредственную связь с процедурами, примененными Коперником. Об этом свидетельствует отрывок из «Краткого изложения Альмагеста» Региомонтана – работы, опубликованной в 1496 г., двадцать лет спустя после смерти ее автора. Птолемеевы модели эпициклов для внутренних планет, как показал Региомонтан, могут быть преобразованы в эксцентрические модели. (Птолемей продемонстрировал это только на примере внешних планет и по какой-то необъяснимой причине отрицал, что аналогичные преобразования можно провести для всех остальных.) Это, предположительно, могло помочь Копернику в разработке его собственной теории, поскольку его доказательства имели много общего (вплоть до ключевых диаграмм) с доказательствами, полученными в XV в. астрономом Али ал-Кушчи, чья карьера началась в Самарканде и закончилась в Константинополе. Он имел некоторую связь с ат-Туси и написал комментарий к его теологическим сочинениям. Высказывалось предположение, что человеком, обеспечившим с помощью этого манускрипта связь между Востоком и Западом, был кардинал Виссарион. Именно он при обстоятельствах, изложенных в главе 10 настоящего издания, впервые предложил Региомонтану написать «Краткое изложение Альмагеста».
86
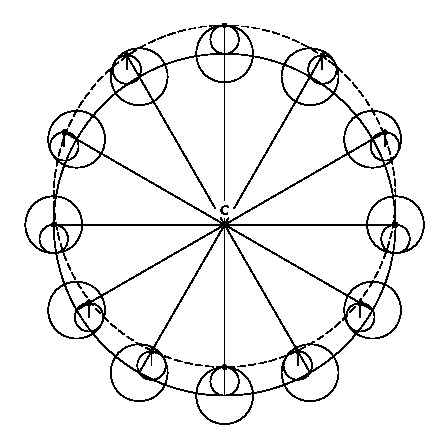
Способ, позволяющий воспроизвести эксцентрическое движение с помощью приема, разработанного Туси
Но вернемся к нашим источникам: вместо детального разбора разнообразных новых планетных моделей выберем в качестве примера только одну из их ключевых функций. Одной из проблем, настоятельно нуждавшихся в решении, являлась замена эксцентрического движения (скажем, круга деферента) комбинацией циклических движений, главный центр которых совпадал бы с Землей – центром Вселенной. Для этого можно было использовать эпициклы (пара которых образовывала бы пару Туси), но необходимо подчеркнуть, что в модели птолемеевого типа это означало введение дополнительного эпицикла. То есть в данном случае речь шла не более чем о замене одного эксцентра другим.
Если выбрать пару Туси с тщательно подобранными размерами и жестко закрепить ее на конце вращающегося радиуса, исходящего из центра (C) круга деферента, то, согласно свойствам пары Туси, осциллирующая точка малого (вращающегося) круга должна будет всегда лежать на вращающейся радиальной линии, проходящей через точку C (ил. 86). На рисунке показано несколько значимых положений такого движения, при условии что скорость «вращательного» движения подобрана таким образом, что точка малого круга задает постоянное направление его радиуса. Тогда точки максимального и минимального удаления от C будут строго противоположны друг другу (апогей и перигей, располагающиеся в верхней и нижней части нашего рисунка соответственно). Ясно, что в этом случае эксцентрический круг, проведенный через указанные противоположные точки, помеченный на рисунке пунктиром, будет почти в точности соответствовать модели, состоящей из трех кругов.
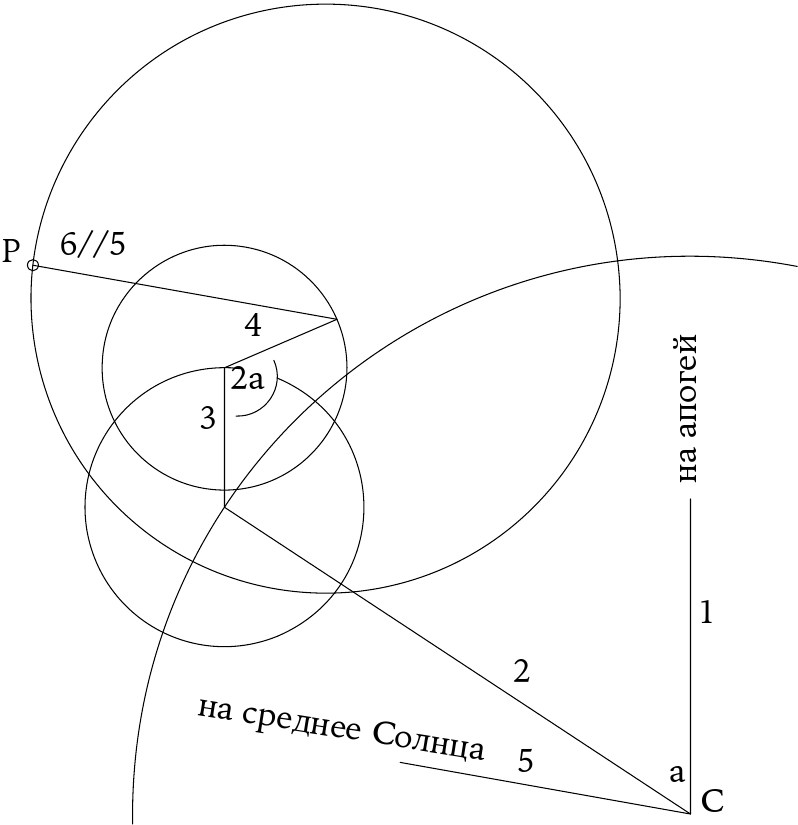
87
Устранение эксцентрического деферента и экванта у Ибн аш-Шатира. Точка C обозначает Землю, а P – планету, положение которой определяется конфигурацией, изображенной на рисунке. Числа введены для обозначения последовательности шагов, которые необходимо совершить, чтобы получить положение планеты. Линии 3 и 6 параллельны линиям 1 и 5 соответственно. Все четыре основные круговые движения на рисунке совершаются против часовой стрелки.
Подобные модели, очевидно, дают широкий простор для обобщений. Вдохновленный техническими приемами ат-Туси, Ибн аш-Шатир пошел еще дальше и устранил не только эксцентричность деферента, но и эксцентричность экванта, введя дополнительные добавочные эпициклы. Он присвоил Солнцу вторичный эпицикл, движущийся по стандартному эпициклу, переносимому деферентом, центр которого в данном случае совпадал с центром Земли. Аналогичным образом, Луна у него обладала двойным эпициклом, но пропорции и движения были, безусловно, другими. Такая лунная модель в той или иной мере способствовала исправлению главного недостатка птолемеевой модели, а именно огромные амплитуды изменения расстояния до Луны – ошибка, которая могла быть обнаружена с помощью простейших наблюдений. Планеты должны были обладать не менее чем тремя эпициклами. Конструкция такого рода с изображением самых необходимых элементов для внешних планет приведена на ил. 87.
После Ибн аш-Шатира мусульманская мода на разработку «допустимых с точки зрения философии» не-птолемеевых схем, похоже, начала постепенно сходить на нет, хотя существуют свидетельства, подтверждающие, что такого рода деятельность продолжалась по меньшей мере до XVI в. Именно тогда она достигла средневековой Европы. В этом можно усмотреть некую не очень понятную многовековую предвзятость, но нужно уметь проводить тонкие различия между всеми ее разновидностями. Предположим, будто нам поручили пронаблюдать осциллирующее движение вдоль прямой линии. Используя некоторые математические формулы, позволяющие получить изменение положений с течением времени, мы, безусловно, сумели бы найти обоснование этого простого прямолинейного движения. Однако «философ» продолжал бы настаивать: оно должно быть объяснено в категориях пары Туси и циклических движений. Мог найтись кто-то, кто пошел бы еще дальше и сказал: вне зависимости от того, имеет ли это какое-либо объяснение, «на самом деле» – это не что иное, как спаренное циклическое движение. Этому последнему персонажу понадобились бы независимые аргументы для обоснования того, «что мы называем реальным». В этом случае астрономы апеллировали к Аристотелю, чья философская рефлексия начиналась с очень простых наблюдений.
Решение, которое может показаться менее спорным, хотя и более слабым с точки зрения философского обоснования, заключается в том, чтобы намеренно стремиться к поиску не более чем рабочего объяснения в рамках теории правильных сфер. Сегодня в подобных случаях нередко звучат высказывания, будто адресоваться нужно не к способности проникновения в сущность вещей, а к эстетическим качествам готовой теории или к ее простоте, а это часто приравнивается друг другу. В прошлые времена такую менее конфликтную альтернативу выбирали, как правило, те, кто разделял аристотелевскую точку зрения на природу реальности и стремился обойти порождаемые ею противоречия.

