Книга: Космос. Иллюстрированная история астрономии и космологии
Назад: ДВИЖЕНИЕ СОЛНЦА ПО ПТОЛЕМЕЮ
Дальше: НЕПОДВИЖНЫЕ ЗВЕЗДЫ У ПТОЛЕМЕЯ
ПТОЛЕМЕЕВА ТЕОРИЯ ДВИЖЕНИЯ ЛУНЫ
Четвертая книга «Альмагеста» содержит подробное обсуждение лунной теории Гиппарха в категориях модели концентрического деферента с новыми параметрами, полученными из наблюдений. В пятой книге, где он переходит к ее сравнению с собственными наблюдениями, Птолемей обнаруживает, что она хорошо работает только тогда, когда Солнце, Земля и Луна находятся на одной линии (в соединении и в оппозиции, или, если называть это одним словом – в сизигиях). Это и не удивительно, если принять во внимание тот факт, что затмения всегда были наиважнейшим фактором в установлении деталей исходной простой модели. Под прямыми углами к этим точкам (в «квадратурах») ошибка достигала нескольких лунных диаметров – отнюдь не самая удовлетворительная ситуация. Здесь Птолемей находит еще одну разновидность движения Луны, известную сегодня как эвекция, и ее открытие можно считать выдающимся достижением, хотя способ ее объяснения, предложенный Птолемеем, оказался не менее замечателен.
61
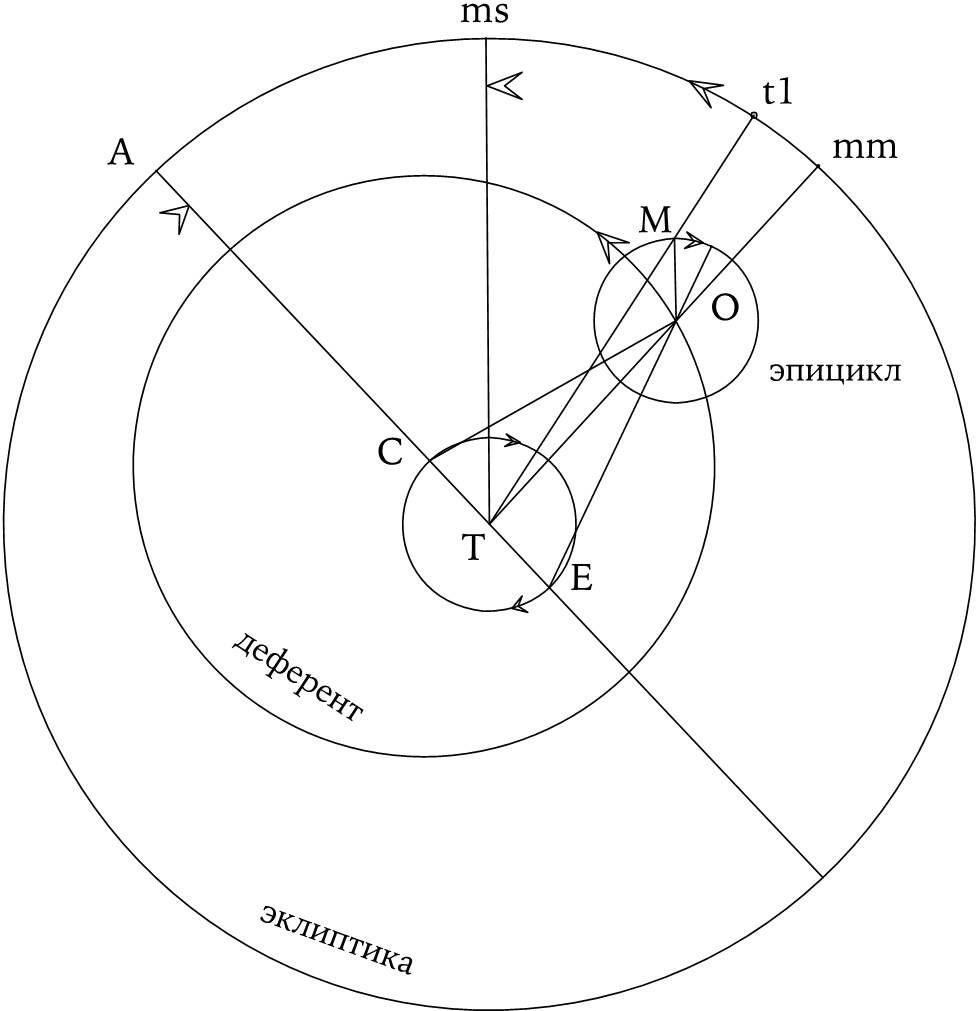
Лунная модель Птолемея. Точка T обозначает Землю, C – (подвижный) центр круга деферента, M – Луну, а E – точку «экванта», вокруг которой центр эпицикла (O) движется с постоянной угловой скоростью. Следует обратить внимание на нетипичное направление кругового вращения Луны в эпицикле. Эпициклам всех планет свойственно «прямое» движение, то есть вращение в противоположном направлении. Среднее эклиптическое положение Луны задается направлением mm, а окончательная истинная долгота – направлением tl.
Подробное изложение его доводов заняло бы слишком много времени, но можно кратко объяснить полученную им итоговую модель. Как и Гиппарх, Птолемей полагал, что Луна должна совершать попятное движение в эпицикле, но, в отличие от Гиппарха, он поместил центр деферента в точку C (как показано на ил. 61), эксцентричную по отношению к Земле и, в свою очередь, движущуюся по малому кругу вокруг Земли, находящейся в точке T. Затем ему понадобилось подобрать скорости, удовлетворительным образом приближавшие бы эпицикл к Земле, когда он находится в квадратуре по отношению к Солнцу. Он сделал это, проведя прямую в направлении среднего Солнца (ms), которая является биссектрисой угла между TO и TC. Следующее уточнение заключалось в том, что он стал вести отсчет постоянно растущего угла в эпицикле не от линии TO, а от линии EO. Это было равнозначно введению еще одной (третьей) вариации. Этим и отличался гений Птолемея – умением добавлять новые параметры к старой модели таким образом, чтобы удовлетворить требуемым условиям. Те, кто хорошо знаком с греческой одержимостью круговым движением, должны оценить методы, посредством которых Птолемей находил возможность преодолеть налагаемые ею ограничения.
Эта модель позволяла получать вполне приемлемые решения для долготы Луны, оказавшиеся лучше, чем все предыдущие. Эклиптика изображена на рисунке для того, чтобы показать, каким образом меняются ключевые долготы. Здесь mm обозначает среднюю Луну, A – движущийся апогей деферента, а tl – итоговую истинную долготу Луны. Однако описанная модель в том виде, как она здесь представлена, содержала один очевидный недостаток: слишком сильное изменение расстояния от Земли до Луны (M), вследствие чего за один полный оборот ее видимый диаметр должен был изменяться в размерах чуть ли не в два раза. Для понимания ошибочности этого не нужно быть астрономом, так как изменения размеров лунного диска на самом деле относительно невелики. Птолемей ничего не говорит об этом. Он достаточно хорошо объяснил изменение долготы, и, кроме того, расположив деферент и эпицикл в плоскости, наклоненной к плоскости эклиптики под углом 5°, он дал хорошее объяснение изменению широты Луны.
Существует распространенное убеждение: он не рассматривал свою модель как нечто, имеющее отношение к описанию реального перемещения тел в пространстве, и она стала не более чем средством расчета координат, и поэтому его не заботили прогнозируемые изменения размеров лунного диска. Однако из работы «Планетные гипотезы» мы узнаем, что Птолемея глубоко беспокоили вопросы, связанные с сотворением планетной системы, содержащей в себе весь сложный эпициклический аппарат небесных тел, в котором не должно было быть пустого пространства. Если он обратил внимание на прогнозируемые изменения размеров Луны, что предполагалось в его модели, – а не заметить этого он просто не мог, – то это непременно послужило для него причиной сильного разочарования.
Пятая книга «Альмагеста» заканчивается обсуждением вопроса о расстояниях до Солнца и Луны и содержит самое раннее подробное теоретическое рассуждение о параллаксе, то есть о поправках, которые необходимо вносить в видимое положение Луны, чтобы получить ее положение относительно центра Земли. (По поводу определения параллакса и открытий Гиппарха в этой области см. с. 157 и ил. 56 и 57. Радиус Земли составляет значительную часть расстояния до Луны. Полученное Птолемеем расстояние до Солнца, выраженное в диаметрах Земли, было сильно занижено – примерно в 20 раз.) Это дало ему возможность перейти к геометрическому описанию затмений. Он начинает с уже теоретически объясненных движений Солнца и Луны и не просто выводит из них обстоятельства, приводящие к затмению, но надеется получить закон их повторения. Птолемею посчастливилось воспользоваться вавилонскими наблюдениями затмений, начиная с эпохи правления Набонасара в 747 г. до н. э. У него не получилось очертить географические границы, в пределах которых возможно наблюдать солнечное затмение. Никто не мог справиться с этой сложной задачей, пока Кассини не занялся ею основательно в середине XVII в. Математические способности Птолемея вполне соответствовали уровню задачи, но у него не было доступа к широкому астрономическому сообществу, которое могло бы стимулировать его для дальнейшего рассмотрения этого вопроса.
Назад: ДВИЖЕНИЕ СОЛНЦА ПО ПТОЛЕМЕЮ
Дальше: НЕПОДВИЖНЫЕ ЗВЕЗДЫ У ПТОЛЕМЕЯ

