Options to TF-IDF similarity

The Best Matching (BM25) algorithm is a probabilistic Information Retrieval (IR) model, while TF-IDF is a vector space model for information retrieval. The probabilistic IR model operates such that, given some relevant and non-relevant documents, we can calculate the probability of a term appearing in a relevant document, and this could be the basis of a classifier that decides whether the documents are relevant or not.

On a practical front, the BM25 model also defines the weight of each term as a product of some term frequency function and some inverse document frequency function and then uses the weight to calculate the score for the whole document with respect to the given query, as follows:

Score = function1(tf) * function2(idf)

The purpose of function1(tf) is to specify a limit on the factor contributing to the score for high-frequency terms. As the term frequency increases, the output of the function in BM25 approaches a limit. Therefore, for high-frequency terms, any further increase in the term frequency does not have much effect on the relevance. The output of the function is such that, for BM25, the increase in tf contribution to the score will be less than that in the TF-IDF model. This means given that the documents and queries are the same across the TF-IDF model and the BM25 model, the factor contributing to the score for term frequency in a document will be higher in the TF-IDF model than that in the BM25 model.

The BM25 model takes an initialization parameter k1 that is used to control or normalize the term frequency. The default value for k1 is 1.2, and it can be changed by passing a separate value.

This is how k1 theoretically affects the term frequency for the ith term in the BM25 algorithm:

tfi = tfi/(k1+tfi)

Another major factor that is used in BM25 is the average document length. BM25 uses document length to compensate for the fact that a longer document in general has more words and is thus more likely to have a higher term frequency, without necessarily being more pertinent to the term and thus no more relevant to the query. However, there may be other documents that have a wider scope and where the high term frequencies are justified. The BM25 similarity accepts another parameter b that is used to control to what degree the document length normalizes term frequency values. Parameter b is used in conjunction with document length dl and average document length avdl to calculate the actual term frequency.

To evaluate the full weight of the term, we need to multiply the term frequency with the IDF. BM25 does IDF differently than the default TF-IDF implementation. If D is the total number of documents in the collection and di is the number of documents containing the ith term in the query, IDFi (for the ith term) is calculated as follows:

IDFi = log(1 + ( (D-di+0.5) / (di+0.5) ))

The full weight of the term is calculated as follows:

Wi = IDFi * boost * TFi

In this case:

TFi = ((k1+1)*tfi) / (tfi + k1(1-b+(b*dl/avdl)))

The default TF-IDF similarity implementation in Lucene does not provide the custom term frequency normalization or document length normalization parameters. This is available in BM25. Tuning the normalization parameters k1 and b can result in better scoring and ranking of documents than that offered by the default TF-IDF similarity formula. It is generally recommended to keep the value of b between 0.5 and 0.8 and that of k1 between 1.2 and 2.

Again it depends on the document collection as to which similarity algorithm would produce better results. The BM25 algorithm is useful for short documents or fields. The best way to determine whether it is good for our collection is to use it in A/B testing with a copy of the same field.

We have already seen the scores for DefaultSimilarity and NoIDFSimilarity earlier in this chapter. Let us implement the BM25 similarity algorithm in our earlier index and see the results. Make the following changes to the schema.xml file. We have modified the values of k1 and b as 1.3 and 0.76, respectively, as follows:

<similarity class=”solr.BM25SimilarityFactory”>         <float name=”k1”>1.3</float>         <float name=”b”>0.76</float> </similarity>

We will need to delete and re-index all the documents. To delete the documents, pass the delete command in the browser URL:

http://localhost:8983/solr/update?stream.body=<delete><query>*:*</query></delete>

http://localhost:8983/solr/update?stream.body=<commit/>

To index the documents again from the exampledocs folder, run the following commands on the console:

 java -jar post.jar *.xml java -Dtype=text/csv -jar post.jar *.csv java -Dtype=application/json -jar post.jar *.json 

On running a search for ipod using BM25 similarity, we get the following output:

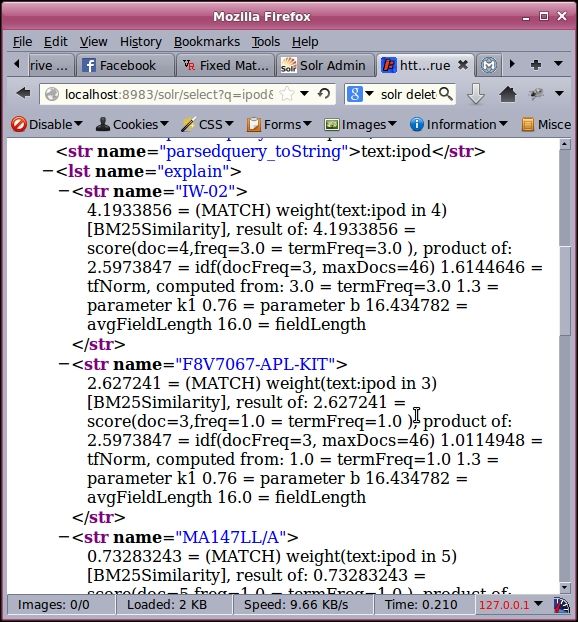
Scores for BM25Similarity

Note that the maximum and minimum scores for BM25similarity are 4.19 and 0.73, respectively. On the other hand, the maximum and minimum scores for DefaultSimilarity are 1.49 and 0.32, respectively. Changing the values of k1 and b will change the scores.

BM25 scoring can be used for short documents. In an e-commerce environment, it can be applied to product names, while the default TF-IDF scoring can be used in product descriptions. Again, the scoring mechanism has to be tweaked by changing k1 and b to obtain the expected search results.

DFR stands for Divergence From Randomness. The DFR concept can be explained as follows. The more the divergence of the within-document term frequency from its frequency within the collection, the more the information carried by word t in document d. The DFR scoring formula contains three separate components—the basic model, the after effect, and an additional normalization component. To construct a DFR formula, we need to specify a value for all the three components mentioned previously.

Possible values for the basic model are:

The possible values for the after effect are:

Additional normalization is also known as length normalization. It has the following options:

In order to use the DFR similarity in Solr, we will need to add the solr.DFRSimilarityFactory class in our schema.xml file. A sample implementation of the DFR similarity is as follows:

<similarity class=”solr.DFRSimilarityFactory”>   <str name=”basicModel”>G</str>   <str name=”afterEffect”>B</str>   <str name=”normalization”>H2</str>   <float name=”c”>7</float> </similarity>

We will need to restart Solr and then delete and index all the documents from the index. On running a search, we should be getting DFRSimilarity in our debug query output.

The DFR scoring algorithm provides a wide variety of tweaking options to choose from while defining the actual algorithm. It is important to choose the appropriate option or options and perform A/B testing to determine which one suits the data and the end user.

In addition to the above discussed similarity classes, we also have other lesser used similarity classes such as IBSimilarity, LMDirichletSimilarity, or LMJelinekMercerSimilarity. We also saw SweetSpotSimilarity earlier in this chapter.