ЧЕХАРДА СО СРЕДНИМИ

Среднее значение может быть весьма полезно, да и разобраться с ним проще, чем с круговой диаграммой. Оно позволяет нам охарактеризовать огромное количество информации одним-единственным числом. Например, мы хотим узнать среднее благосостояние людей в комнате, чтобы понять, принесет ли встреча с ними какую-нибудь пользу нашим фандрайзерам или менеджерам по продажам. Другой пример: мы хотим узнать среднюю цену на бензин, чтобы оценить, во сколько обойдется поездка на машине из Ванкувера в Банф. Однако средние могут быть обманчиво сложными.

Есть три вида средних, и они могут выражаться разными числами. Поэтому те, кто всерьез занимается статистикой, избегают слова «среднее», отдавая предпочтение другим, более точным терминам, как то: среднее арифметическое, медиана или мода. И только так. Иногда все эти величины совпадают, но чаще они различаются. Если вам встретилось слово «среднее», оно, как правило, означает «среднее арифметическое», но нельзя быть в этом абсолютно уве­ренным.

Чаще других из этих трех встречается среднее арифметическое; оно равно сумме всех данных, поделенной на их количество. Например, среднее благосостояние всех людей, находящихся в комнате, будет равно их общему благосостоянию, поделенному на количество человек. Если в комнате находится десять человек, состояние каждого из которых оценивается в 100 тысяч долларов, то общее богатство составит миллион. Отсюда легко вычислить среднее арифметическое (даже доставать калькулятор не нужно): 100 тысяч долларов. А если состояние каждого присутствующего будет варьироваться от 50 тысяч до 150 тысяч долларов, но общее количество будет по-прежнему миллион, то среднее арифметическое по-прежнему будет 100 тысяч долларов (потому что мы просто разделим миллион на десять, не принимая во внимание, сколько денег на счете у каждого).

Медиана — это число в середине упорядоченного набора чисел (статистики называют его выборкой): половина данных находится ниже этого значения, а половина выше. Как вы помните, смысл среднего значения в том, чтобы охарактеризовать весь объем данных одним-единственным числом. Медиана лучше с этим справляется, если некоторые из ваших данных уж очень отличаются от большинства, статистики называют такие значения выбросами.

Представим себе комнату, в которой находятся девять человек; состояние восьмерых из них равно примерно 100 тысяч долларов, а один находится на грани банкротства, его долг равен 500 тысячам долларов. Вот что у нас получится:

Человек 1: –500 тыс. долл.

Человек 2: 96 тыс. долл.

Человек 3: 97 тыс. долл.

Человек 4: 99 тыс. долл.

Человек 5: 100 тыс. долл.

Человек 6: 101 тыс. долл.

Человек 7: 101 тыс. долл.

Человек 8: 101 тыс. долл.

Человек 9: 104 тыс. долл.

Теперь складываем все показатели и получаем общую сумму в 299 тысяч долларов. Разделим это число на общее количество участников, девять, и получится, что среднее арифметическое равно 33 222 долларам. Создается, однако, впечатление, что среднее арифметическое — не лучший способ охарактеризовать данные о присутствующих. Смею предположить, что фандрайзер не захочет наносить им визит, если среди них найдется человек с показателем-выбросом, который тянет вниз всю группу. В этом и заключается вся трудность работы со средним арифметическим: оно слишком чувствительно к выбросам.

Медиана здесь равна 100 тысячам долларов: четверо зарабатывают меньше этой суммы, а четверо — больше. Мода равна 101 тысяче долларов — это та цифра, которая появляется намного чаще других. И медиана, и мода в этом конкретном примере оказываются гораздо показательнее.

Можно по-разному использовать средние, особенно если вы хотите, чтобы кто-то увидел в ваших данных то, что нужно вам.

Давайте представим, что вы с двумя друзьями запустили стартап — небольшую компанию, в которой работают пять человек. Сейчас конец года, вы собираетесь подвести финансовые итоги и рассказать сотрудникам, как у компании идут дела, чтобы они почувствовали удовлетворение от долгих часов, проведенных в офисе, и от холодной пиццы, съеденной за это время. А еще вы хотите привлечь инвесторов. Скажем, четверо сотрудников — все программисты — за год заработали по 70 тысяч долларов, а один — офис-менеджер — 50 тысяч. Это даст среднее арифметическое зарплат, равное 66 тысячам долларов в год: сумма (4 × 70 000) + (1 × 50 000), поделенная на 5. Вы и двое ваших друзей принесли домой по 100 тысяч долларов — это ваша зарплата. Следовательно, общая сумма выплаченных зарплат составит (4 × 70 000) + (1 × 50 000) + (3 × 100 000) = 630 тысяч долларов. Кроме того, пусть ваша компания принесла 210 тысяч долларов чистого дохода, который вы разделили поровну между собой и соучредителями в качестве бонусов, это дает каждому из вас по 100 тысяч + 70 тысяч. Как вы им об этом сообщите­?

Вы могли бы сказать:

средняя зарплата сотрудников составляет 66 тысяч долларов;

средняя зарплата + прибыль владельцев составляет 170 тысяч долларов.

И хотя это правда, вряд ли новость понравится кому-нибудь, кроме вас и вашей мамы. Если ваши подчиненные прознают об этом, то решат, что им существенно недоплатили. А потенциальные инвесторы сочтут, что учредителям платят слишком много. Поэтому вы можете оформить отчет по-другому:

средняя зарплата сотрудников составляет 66 тысяч долларов;

средняя зарплата владельцев составляет 100 тысяч долларов;

прибыль: 210 тысяч долларов.

Для потенциальных инвесторов это выглядит убедительнее, тем более что им можно и не говорить о том, что вы поделили прибыль между совладельцами. А сотрудникам последнюю строку можно и вовсе не показывать. Каждый из четырех программистов будет думать, что он на хорошем счету и его ценят, так как зарабатывает он больше, чем большинство. Единственный, кто будет не очень доволен, — ваш офис-менеджер. Но ведь девушка и раньше понимала, что программисты зарабатывают больше нее. Теперь представим: вы чувствуете, что перегружены работой, и хотите уговорить ваших партнеров, которые не сильны в критическом мышлении, что вам нужно нанять еще сотрудников. Вы можете поступить так же, как в таком случае делают многие компании, и заявить о «прибыли на одного сотрудника», поделив прибыль компании, равную 210 тысячам долларов, на пятерых­:

средняя зарплата сотрудника: 66 тысяч долларов;

средняя зарплата владельцев: 100 тысяч долларов;

годовая прибыль на одного сотрудника: 42 тысячи долларов.

Теперь вы можете заявить, что 64% зарплаты, которую вы выплачиваете своим сотрудникам (42 000 / 66 000), возвращаются к вам в виде прибыли, и это означает, что в итоге, получив прибыль, вы должны будете выплатить только 36% их зарплат. Конечно, эти данные не свидетельствуют о том, что, наняв еще сотрудников, вы увеличите прибыль. Но в глазах того, кто не очень силен в критическом мышлении, это выглядит как весомый довод для увеличения штата.

А что, если вы хотите выглядеть невероятно честным и справедливым работодателем и показать, что разница между вашей прибылью и зарплатой ваших сотрудников довольно разумна? Возьмите прибыль в 210 тысяч долларов и разделите часть этой суммы, 150 тысяч долларов, в качестве бонуса между собой и своими партнерами. Об оставшихся 60 тысячах вы скажете позже, что это и есть «прибыль». На этот раз подсчитайте среднюю зарплату, включив в эти подсчеты себя и своих партнеров вместе с бонусами:

средняя зарплата: 97 500;

средняя прибыль владельцев компании: 20 тысяч.

А теперь повеселимся по-настоящему:

общие выплаты зарплат плюс бонусы: 840 тысяч;

зарплаты: 780 тысяч;

прибыль: 60 тысяч.

Теперь все выглядит разумно, правда? Из всей суммы в 840 тысяч долларов, включающей зарплату и прибыль, только 60 тысяч, или 7%, составили личную прибыль владельцев. Ваши сотрудники будут думать, что вы безупречны, — кто станет обвинять владельца компании в том, что он присвоил 7%? По сути, это ведь не так уж много: 7% делится между владельцами компании поровну, и каждый получает по 2,3%. Да тут даже возразить нечего!

А можно придумать и кое-что получше. Представьте, что в первый год существования вашей компании у вас были только сотрудники, работавшие неполный день. Они зарабатывали по 40 тысяч в год. На второй год у вас были только сотрудники, работавшие полный день. И они получали 66 тысяч, о которых говорилось выше. В таком случае вы со всей уверенностью можете заявить, что в среднем заработок каждого сотрудника увеличился на 65%. Вы — великий предприниматель! Правда, вы замалчиваете тот факт, что сравниваете две несопоставимые вещи: работу на неполный и полный рабочие дни. Могу сказать, что в этом вы не первый: американская корпорация по производству стали U.S. Steel додумалась до этого еще в 1940-х годах.

В уголовном судопроизводстве то, как представлена информация, т. е. фрейминг, оказывает сильное воздействие на мнение присяжных относительно виновности подсудимого. Хотя математически эти два утверждения эквивалентны, фраза: «Вероятность того, что обнаруженная на месте преступления кровь совпадет с кровью подозреваемого, если только это действительно не его кровь, составляет всего 0,1%» (один к тысяче) гораздо убедительнее, чем заявление: «Кровь одного человека из каждой тысячи жителей Хьюстона тоже соответствует найденной».

Средние часто используют для того, чтобы рассказать о результатах, например «один брак из X случаев заканчивается разводом». Но это не означает, что статистика применима к вашей улице, к вашему бридж-клубу или к вашему знакомому. Брак либо закончится разводом, либо нет, но нужно знать определенные факторы уязвимости, чтобы предсказать, кто действительно разведется, а кто нет.

Еще один пример: вы можете прочитать, что один из пяти новорожденных детей — китаец. Вы подмечаете, что у шведского семейства, живущего на вашей улице, уже есть четверо детей, а сейчас они ждут пополнения. Но это не означает, что в семье родится маленький китаец. Среднее значение вычислено по всем рождениям в мире, а не в конкретной семье, в конкретном доме, в конкретном районе или даже стране.

Будьте осторожны со средними, а также с тем, как их интерпретируют. Один из способов ввести в заблуждение, используя средние, — усреднять данные по выборкам из несопоставимых совокупностей. Этот способ может привести к абсурдным выводам, как то:

В среднем у каждого человека одно яичко.

Этот пример наглядно показывает разницу между средним арифметическим, медианой и модой. Так как женщин в мире несколько больше, чем мужчин, медиана и мода будут равны нулю, в то время как среднее арифметическое будет близко к единице (возможно, оно будет равно 0,98 или около того).

Кроме этого, нужно быть внимательным и помнить, что среднее ничего не говорит о размахе значений. Средняя годовая температура в Долине Смерти в Калифорнии равна 25 °С, что считается комфортным. Но размах может быть просто убийственным, с колебанием температуры от –9 до 57 °C, — факт, зафиксированный приборами.

Или… Я мог бы вам сказать, что в среднем благосостояние сотни людей, находящихся в комнате, составляет колоссальную сумму: 350 миллионов долларов. Вы, наверное, думаете: вот бы отправить туда моих лучших менеджеров по продажам. Но в комнате могут находиться Марк Цукерберг (его состояние оценивается в 25 миллиардов долларов) и 99 бедняков. Таким образом, средний показатель может размыть разницу в важных показателях.

Если вы работаете со средними, остерегайтесь еще бимодального распределения. Вспомните, мода — это то значение, которое встречается чаще всего. Во многих наборах данных — биологических, физических, социальных — у распределения может быть два или больше пиков. А это значит, что два или больше показателей встречаются чаще других.

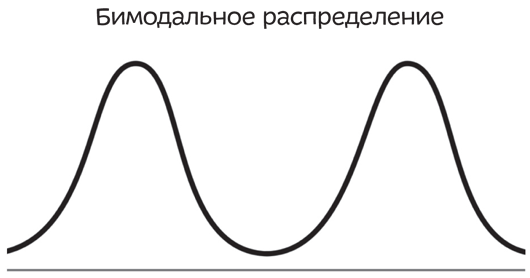
Например, подобный график может отображать сумму, потраченную на обеды в неделю (ось X), и количество людей, потративших такую сумму (ось Y). Представьте, что вы изучали две группы людей: детей (левый горб) — они покупают школьные обеды — и руководителей компаний (правый горб) — они ходят в дорогие рестораны. Среднее арифметическое и медиана в данном случае — это числа где-то между этими двумя горбами, и они ничего не скажут нам о том, что происходит на самом деле, — ведь во многих случаях среднее арифметическое и медиана отражают ту сумму, которую никто не тратит. Подобный график говорит лишь о том, что в вашем примере имеет место неоднородность — вы сравниваете яблоки с апельсинами. В таком случае лучше сразу сказать, что вы имеете дело с бимодальным распределением, и сообщить о двух модах. А еще лучше разделить группу на две подгруппы и собрать статистические данные для каждой.

Будьте осторожны, когда будете делать выводы об отдельных людях и о группах, основываясь на средних данных. Тут можно легко наткнуться на определенные подводные камни, которые даже получили собственные названия: «экологическая ошибка» и «ошибка исключения». Экологическая ошибка возникает, если мы делаем выводы об отдельном элементе, основываясь на совокупных данных (таких как средняя величина группы), а ошибка исключения — если делать все ровно наоборот.

Представьте себе, например, два маленьких городка, в каждом из которых живет всего по сотне человек. Девяносто девять жителей города А зарабатывают по 80 тысяч долларов в год, а на земле одной женщины было найдено месторождение нефти, и теперь она одна получает 5 миллионов долларов в год. В городе Б живут 50 человек, которые зарабатывают по 100 тысяч долларов в год, а также 50 человек, которые получают по 140 тысяч долларов. Средний арифметический доход в городе А составляет 129 тысяч долларов, а в городе Б — 120 тысяч долларов. И хотя средняя величина доходов города А больше, в 99 случаях из 100 доход любого жителя города Б, которого вы выберете наугад, будет выше дохода любого случайно выбранного жителя города А. Экологическую ошибку совершают те, кто считает, что если выбрать наугад человека из группы с более высоким средним доходом, то следует ожидать, что и у него доход будет выше. Самое замечательное в этом примере то, что в городе А выше среднее арифметическое, а мода выше в городе B (так бывает не всегда).

Вот еще один пример: считается, что состоятельные люди скорее проголосуют за республиканца, но, как показывает практика, более состоятельные штаты обычно голосуют за демократов. Дело в том, что общая картина благосостояния жителей процветающих штатов может быть немного перекошена из-за суперсостоятельных индивидуумов. Во время президентских выборов 2004 года за кандидата от Республиканской партии Джорджа Буша проголосовали 15 самых бедных штатов, а за кандидата от Демократической партии Джона Керри — девять из 11 самых состоятельных. Если же изучить вопрос более детально, мы увидим, что за Буша отдали голоса 62% тех, чей годовой доход составляет более 200 тысяч долларов, а за Керри — 36% голосующих, зарабатывающих в год 15 тысяч долларов или меньше.

Чтобы понять, что такое ошибка исключения, давайте представим себе: вы прочли, что машины марки Volvo считаются самыми надежными, и решили купить такой автомобиль. По дороге в офис этой компании вы проходите мимо механика Volvo и парковки, заполненной машинами этой марки, которые ждут, пока их отремонтируют. Если вы измените свое решение о покупке машины этой марки, основываясь на том, что только что увидели, значит, вы по небольшому числу исключительных данных формируете выводы о целой группе. Никто ведь не говорил, что Volvo вообще не нуждается в ремонте, — скорее речь шла о следующем: вероятность того, что им может понадобиться техническая поддержка, гораздо меньше (отсюда и набившее оскомину предупреждение, которым заканчивается любой рекламный ролик, что «каждая машина индивидуальна»). Обратите внимание, что на вас оказывают огромное влияние и другим образом: единственное место, где должны стоять машины Volvo, требующие ремонта, — автосервис Volvo. Ваш «базовый показатель» сдвинулся, и вы не можете уже считать этот пример случайным.

Сейчас, когда вы уже эксперт по средним, вас не удивит заявление, что 100 лет назад наши предки жили меньше, чем мы сегодня. Возможно, вы читали, что продолжительность жизни в наше время сильно увеличилась. Продолжительность жизни тех, кто родился в 1850 году, была 38 лет для мужчин и 40 для женщин, а у тех, кто родился в 1990-м, она составляет 72 года и 79 лет соответственно. Таким образом, возникает распространенное заблуждение, что в XIX веке было не так много людей в возрасте 50 и 60 лет, потому что они просто не доживали до этого возраста. На самом деле, конечно, доживали — просто детская смертность была такой высокой, что смещала средний показатель. Если человеку удавалось преодолеть возрастной рубеж в 20 лет, то жил он долго. В 1850 году 50-летняя белая женщина могла бы дожить до 73 с половиной лет, а женщина 60 лет — и до 77. По сравнению с 1850-ми годами сейчас продолжительность жизни 50- и 60-летних значительно увеличилась, лет на десять, и произошло это во многом благодаря более качественному здраво­охранению.

Но так же, как и в примере с комнатой, полной людей с совершенно разными доходами, изменение средней продолжительности жизни за последние 175 лет отражает большие изменения в структуре населения. В то время уровень детской смертности был гораздо выше, что и снижало среднюю продолжительность жизни. Вот вам парадокс: средний ребенок никогда не рождается в средней семье. Почему? Из-за того, что рассматриваются разные группы. (Я здесь использую понятие «среднее» вместо «среднее арифметическое» из уважения к прекрасной работе, написанной по этой теме Джеймсом Дженкинсом и Терреллом Тьютеном, которые использовали это понятие в заголовке.)

Теперь давайте представим, что вы прочли, будто среднее число детей в семье, живущей где-то в пригороде, равно трем. Скорее всего, вы сделаете вывод, что в среднем у ребенка должно быть двое братьев и сестер. Но это заключение будет неверным. Та же логическая ошибка возникает в случае, если мы спросим, посещает ли средний студент колледжа колледж среднего размера, получает ли средний сотрудник среднюю зарплату или растет ли среднее дерево в среднем лесу. В чем же дело?

Во всех этих случаях меняется точка отсчета — та группа, которую мы изучаем. Когда подсчитывают среднее количество детей в семье, выборка состоит из семей. Независимо от того, большие это семьи или маленькие, все равно это будут семьи. А когда подсчитывают среднее количество братьев и сестер у одного ребенка, выборка состоит из детей. Учитывается каждый ребенок в большой семье; таким образом, количество детей в каждой семье сильно влияет на средний показатель количества братьев и сестер. Иными словами, семья с десятью детьми считается один раз в средней семейной статистике, но десять раз в статистике, отражающей количество братьев и сестер у одного ребенка. Предположим, что в одном районе этой гипотетической общины живут 30 семей. У четырех из них нет детей, в шести — по одному ребенку, в девяти — по два, и в 11 семьях воспитывается по шестеро детей. В среднем в каждой семье по три ребенка, потому что нужно разделить 90 (общее количество детей) на 30 (общее количество семей).

Но давайте посмотрим на среднее число братьев и сестер у одного ребенка. Мы часто допускаем ошибку, думая, что если в среднем в семье по три ребенка, то у каждого из них должно быть двое братьев или сестер. Но в семьях с одним ребенком на каждого из шести детей приходится ноль братьев и сестер. В семьях с двумя детьми на каждого из 18 детей приходится по одному брату или сестре. В семьях с шестью детьми на каждого из 66 детей приходится пять братьев и сестер. У 90 детей, выходит, 348 братьев или сестер. Следовательно, хотя средний ребенок воспитывается в семье с тремя детьми, на 90 детей приходится 348 братьев и сестер, или в среднем приблизительно четыре брата или сестры на ребенка.

	Семей	Детей в семье	Всего детей	Братьев и сестер
	4	0	0	0
	6	1	6	0
	9	2	18	18
	II	6	66	330
Всего	30		90	348

Среднее количество детей на семью: 3,0
Среднее количество братьев и сестер на ребенка: 3,9

А теперь давайте рассмотрим пример с колледжами. В Соединенных Штатах множество крупных колледжей (например, колледж в штате Огайо или в штате Аризона), где учится более 50 тысяч студентов. Есть также и не такие большие колледжи, где учится менее 3 тысяч студентов (например, Кеньон-колледж или Уильямс-колледж). Если мы включим в наши подсчеты еще и школы, то получим, что в колледже среднего размера учится 10 тысяч студентов. Но если подсчитать количество студентов, то получится, что средний студент ходит в колледж, где учится более 30 тысяч студентов. Это происходит потому, что при подсчете студентов мы получим гораздо больше данных из крупных школ. Схожим образом можно сделать вывод, что средний человек не живет в среднем городе, а средний гольфист не делает среднее число ударов для прохождения площадки с 18 лунками.

Во всех этих примерах меняется изучаемая группа, а потому меняется знаменатель при вычислении среднего арифметического. Рассмотрим еще один пример асимметричного распределения вроде того, с которым мы встретились, обсуждая детскую смертность: средний инвестор не получает средний доход.

В одном исследовании средний доход от инвестиции 100 долларов на срок 30 лет составил 760 долларов, или 7% в год. Но 9% инвесторов потеряли деньги, а огромному числу инвесторов, 69%, не удалось достигнуть показателя среднего дохода. Так случилось потому, что среднее арифметическое было смещено из-за нескольких человек, заработавших больше среднего. На графике, предложенном ниже, среднее арифметическое смещено вправо благодаря тем счастливчикам, которым удалось заработать состояние.

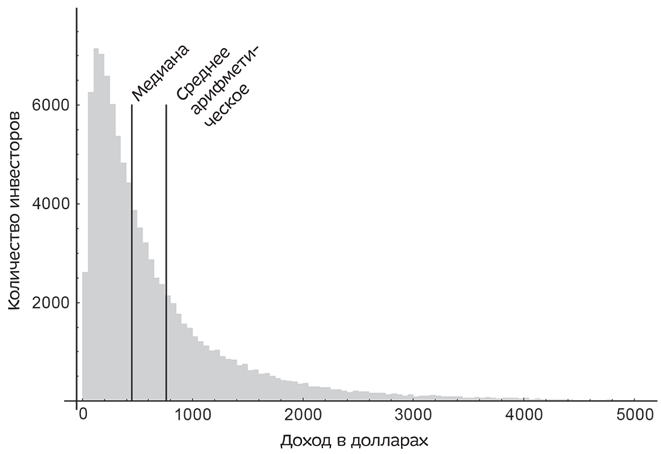
Доходность инвестиции в 100 долларов через 30 лет. Обратите внимание: большинство людей получили доход меньше среднего арифметического, а немногие счастливчики — в пять раз больше среднего.

Отправить