БАЙЕСОВСКИЙ МЕТОД В НАУКЕ И В СУДЕ
Вспомните часть 1 и описанную в ней , в которой вы можете поменять свою уверенность в чем-либо, основываясь на новых данных или же на априорной вероятности того, что что-то верно, — например, вероятности, что у вас пневмония при условии, что у вас наблюдаются определенные симптомы, или вероятности того, что какой-то человек будет голосовать за конкретную партию с учетом своего места жительства.
Пользуясь байесовским методом, мы назначаем гипотезе субъективную вероятность (априорную), а затем уточняем ее в свете собранных данных (апостериорная вероятность, потому что именно эти данные мы получаем, проведя эксперимент). Если бы у нас еще до проверки имелись основания верить, что гипотеза правильна, то нам было бы легко подтвердить ее при наличии небольшого количества доказательств. Если бы еще до проверки у нас были основания считать гипотезу маловероятной, то нам понадобилось бы больше доказательств.
Таким образом, согласно байесовской теории, маловероятные утверждения требуют большей доказательной базы, чем те, что заслуживают большего доверия. Предположим, ваша подруга говорит, что она видела, как что-то пролетело за окном. Вы можете выдвинуть три гипотезы с учетом ваших знаний об этом окне: это могли быть малиновка, воробей или свинья. И для всех этих гипотез вы можете назначить вероятности. И вот ваша подруга показывает вам фотографию свиньи, пролетающей за окном. Ваша априорная вероятность, что свиньи летают, была настолько мала, что и апостериорная вероятность оказалась не больше, даже при наличии доказательства. Возможно, сейчас вы уже выдвигаете новые гипотезы, что фотография была поддельной или что ваша подруга применила какой-то другой трюк. И если вся эта история напомнила вам четырехчастную табличку и вероятность, что у кого-то рак молочной железы при условии, что результаты тестов были положительными, то вы правильно мыслите — четырехчастные таблички прекрасно помогают проверить какие-то данные с помощью байесовского метода.
Ученым следует быть гораздо требовательней к тем доводам, которые идут вразрез со стандартными теориями или моделями, нежели к тем, что согласуются с ними. Зная, что при исследовании нового ретровирусного лекарства были проведены тысячи успешных экспериментов на мышах и обезьянах, мы не сильно удивляемся, когда обнаруживается, что оно хорошо воздействует и на человека, — мы охотно принимаем доказательство исходя из принятых стандартов. Нас может убедить одно-единственное исследование, в котором приняли участие лишь несколько сотен человек. Но если один человек скажет, что сидение в течение трех дней у изножья пирамиды вылечит СПИД — при правильном циркулировании энергии ци в чакрах, — тут нам нужно будет больше доказательств, потому что утверждение выглядит надуманным и ни о чем таком мы раньше не слышали. Мы бы захотели видеть результат, воспроизводимый много раз и в самых разных условиях, а еще лучше — метаанализ.
Байесовский подход — не единственный, с помощью которого ученые доходят до сути в случае с чем-то маловероятным. В поисках бозона Хиггса физики установили пороговую величину (используя традиционные, не байесовские, статистические тесты), которая была в 50 раз выше обычного, — не потому, что существование бозона было маловероятно (гипотезы о его существовании выдвигались десятилетиями), а потому, что цена ошибки была слишком высока (необходимо было провести очень дорогостоящие эксперименты).
Применение правила Байеса, возможно, лучше всего можно проиллюстрировать на примере из судебной практики. Один из краеугольных принципов судебного дела был сформулирован французским врачом и юристом Эдмоном Локаром: любой контакт оставляет след. По его мнению, правонарушитель либо оставляет следы на месте преступления, либо забирает их с собой — на себе, на одежде, — и тогда можно легко понять, где он был и что делал.
Предположим, злоумышленник пробрался в конюшню, чтобы дать допинг лошади накануне большой гонки. Он наверняка оставит следы на месте преступления — отпечатки ботинок, возможно, частички кожи, волос, ниточки от одежды и пр. Иными словами, улики переходят с преступника на место преступления. А также он сам, скорее всего, запачкается, на его одежде останутся следы конских волос, ниточки от попоны, щепки или солома из стойла — то есть улики с места преступления перейдут на преступника.
А теперь представим себе, что кого-то арестовали на следующий день. Были взяты образцы ткани, отпечатки пальцев, грязь из-под ногтей — и в результате анализа обнаружились некоторые совпадения между этими образцами и теми, что были взяты с места преступления. Прокурор хочет определить, насколько весомы улики. Возможно, совпадение объясняется тем, что подозреваемый виновен. Или, если он не виновен, он мог находиться в контакте с преступником — подобное сотрудничество тоже не может остаться бесследным. Или, как вариант, подозреваемый находился на другой конюшне, совершенно невинно контактируя с другой лошадью, — а тесты показали сходство образцов.
С помощью байесовского метода мы можем сочетать объективные вероятности (такие как вероятность того, что ДНК подозреваемого совпадет с той, что была найдена на месте преступления) с личным субъективным мнением о надежности показаний свидетеля, а также честности и опыте криминалиста, хранившего образец ДНК. Совершал ли подозреваемый что-нибудь подобное раньше или он не знает ничего о забеге, не знаком ни с одним участником гонки и может предоставить убедительное алиби? Благодаря этим факторам мы можем говорить об априорной субъективной вероятности, что подозреваемый виновен.
Если взять буквальное значение слова «невиновный», принятое в американском законодательстве (тот, чью вину не доказали), то априорная вероятность того, что подозреваемый виновен, будет равна нулю, а любая улика, не важно, насколько она изобличающая, не поднимет последующую вероятность выше нуля, потому что вы все время будете умножать на нуль. Выдвигая априорную гипотезу о невиновности подозреваемого, гораздо разумнее будет предположить, что любой человек из той же совокупности с равной вероятностью может оказаться виновным. Следовательно, если подозреваемый был задержан в городе с населением 100 тысяч человек, а у следователя есть причина верить, что преступник жил в этом городе, то априорная вероятность того, что подозреваемый виновен, будет один к 100 тысячам. Конечно, улики могут сузить совокупность — например, нам может быть известно, что не было следов взлома, следовательно, подозреваемый должен быть одним из 50 человек, имевших доступ к конюшне.
Наша априорная гипотеза состоит в том, что подозреваемый виновен с вероятностью 0,02 (один из 50 человек, имевших доступ). А теперь представим, что нашему злоумышленнику пришлось попотеть, чтобы справиться с лошадью, и на месте преступления остались следы крови. Как уверяют судебные эксперты, вероятность того, что образец крови подозреваемого совпадет с образцом, взятым на месте преступления, равна 0,85. Мы чертим четырехчастную табличку, как делали это раньше, и заполняем в первую очередь нижнюю строку под ней: один из 50 шансов за то, что подозреваемый виновен (виновен: столбец «да»), и 49 шансов из 50 за то, что невиновен. В лаборатории нам сообщили, что вероятность совпадения образов крови 0,85, — вписываем эти данные в верхнюю левую ячейку: вероятность того, что подозреваемый виновен и образцы совпадают. Это означает, что в нижнюю левую ячейку надо записать 0,15 (сумма вероятностей должна давать единицу). Совпадение образцов на 85% означает, что с вероятностью 15% кровь была оставлена кем-то еще, не нашим подозреваемым, — а значит, его можно оправдать. А еще есть 15% вероятности, что следы крови оставил кто-то из оставшихся 49 человек, поэтому мы умножаем 49 на 0,15 и получаем 7,35 — вписываем это число в правую верхнюю ячейку. Мы вычитаем его из 49, чтобы найти значение, которое запишем внизу справа.
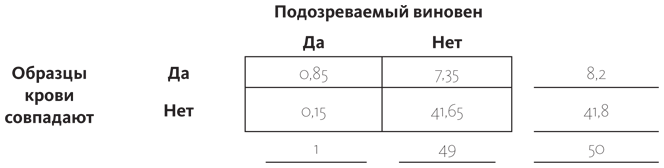
Теперь мы можем вычислить данные, которые должны будут оценить судья и присяжные.
P (Виновен | Совпадение ) = 0,85 / 8,2 = 0,10
P (Невиновен | Совпадение) = 7,35 / 8,2 = 0,90
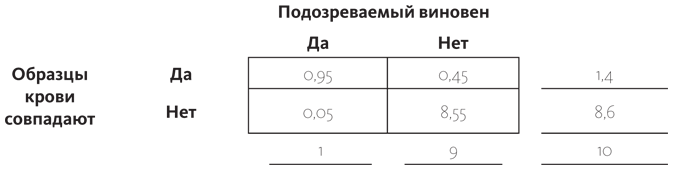
С учетом улик вероятность невиновности подозреваемого в девять раз выше, чем виновности. Начинали мы с 2%-ной вероятности, что он виновен, новая информация увеличила эту вероятность в пять раз, но все же вероятность того, что он невиновен, больше. Давайте представим, что у нас появились дополнительные улики — конский волос, найденный на пальто подозреваемого, — а вероятность того, что это шерсть лошади, получившей допинг, равна 0,95 (шансы, что он принадлежит другой лошади, — пять из 100). Теперь мы можем увязать все байесовские вероятности друг с другом, заполнив новую табличку. В нижней строке вписываем те значения, которые только что получили путем математических подсчетов: 0,10 и 0,90 (статистики иногда шутят, что вчерашние апостериорные события — это сегодняшние априорные). Если вы скорее склонны интерпретировать эти цифры как «один шанс из десяти» и «девять шансов из десяти», смело вписывайте целые числа.
Мы знаем от наших судебных экспертов, что вероятность совпадения образцов волос равна 0,95. Умножив это на 1, мы получаем данные, которые вписываем в верхнюю левую ячейку, а вычитая результат из единицы, получаем значение для нижней левой ячейки. Если вероятность того, что образец совпадает с образцом лошади-жертвы, равна 0,95, то с вероятностью 0,05 образец совпадет с образцом другого животного (благодаря чему подозреваемый будет оправдан). Значит, в правую верхнюю ячейку мы вписываем 0,45 — результат умножения 0,05 на число внизу таблицы, то есть на девять. Теперь, закончив вычисления, мы видим следующее:
| P (Виновен | Улика ) = 0,68 | P (Улика | Виновен) = 0,95 |
| P (Невиновен | Улика) = 0,32 | P (Улика | Невиновен) = 0,05 |
Новые улики показывают, что вероятность виновности подозреваемого в два раза выше, чем вероятность его невиновности. Многие прокуроры и судьи не знают, как работать с уликами, используя таблички, но вы видите, насколько это полезно. Ошибочное мнение, что P (Виновен | Улика) = P (Улика | Виновен), настолько распространено, что даже получило название «ошибка прокурора».
Если вам так удобнее, правило Байеса можно использовать чисто математически, не прибегая к четырехчастной табличке. Как это сделать, описано в .