ГЛАВА 3
НАУКА О МНОЖЕСТВЕ МОДЕЛЕЙ
Нет ничего менее реального, чем реализм. Детали вводят в заблуждение. Только путем отбора, исключения, акцента мы постигаем истинный смысл вещей.
Джорджия О’Кифф
В этой главе мы научно обоснуем эффективность многомодельного подхода. И начнем с теоремы Кондорсе о жюри присяжных и теоремы о прогнозе разнообразия, которые содержат поддающиеся количественной оценке аргументы в пользу ценности множества моделей как помощников в принятии решений, прогнозировании и объяснении. Однако эти теоремы могут преувеличивать такие аргументы. Чтобы объяснить, почему, мы обратимся к моделям категоризации, которые делят мир на блоки. Применение моделей категоризации покажет, что построение множества моделей может оказаться более сложной задачей, чем мы предполагали. Использование этого же класса моделей позволит нам обсудить степень их детализации (насколько точными они должны быть), а также решить, применять ли одну большую модель или несколько маленьких. Выбор будет зависеть от области применения. При прогнозировании мы часто стремимся действовать с размахом. В случае объяснения разумнее руководствоваться принципом «чем меньше, тем лучше».
Этот вывод решает одну давнюю проблему. На первый взгляд может показаться, что многомодельное мышление требует изучения большого количества моделей. Хотя нам действительно нужно освоить некоторые модели, их не так много, как вы думаете. Нам не придется изучать сто или даже пятьдесят моделей, поскольку они обладают важным свойством, известным как «один ко многим». Мы можем применять одну и ту же модель в разных ситуациях, введя новые переменные, параметры и изменив допущения. Это свойство в какой-то мере противоречит идее многомодельного мышления. Использование модели в новой области требует креативности, открытости разума и скептицизма. Мы должны признать, что не каждая модель подходит для решения любой задачи. Если модель не может объяснить, спрогнозировать или помочь нам рассуждать, ее нужно исключить из рассмотрения.
Навыки, необходимые для использования одной модели во многих областях, отличаются от математических и аналитических способностей, наличие которых многие считают обязательным условием для достижения успеха в моделировании. Процесс использования одной модели во многих областях подразумевает творческий подход. Прежде всего задайте себе вопрос: «Сколько областей применения я могу найти для модели случайного блуждания?» Чтобы вы могли составить представление о том, какие формы может принимать креативность, в конце главы мы используем геометрическую формулу площади и объема в качестве модели и применим ее для объяснения размера супертанкеров, критики индекса массы тела, прогноза масштабирования метаболизма и объяснения, почему так мало женщин-руководителей.
МНОЖЕСТВО МОДЕЛЕЙ КАК НЕЗАВИСИМЫХ СЛУЧАЕВ ЛЖИ
Теперь обратимся к моделям, которые помогают раскрыть преимущества многомодельного мышления. И представим в их контексте две теоремы: теорему Кондорсе о жюри присяжных и теорему о прогнозе разнообразия. Теорема Кондорсе о жюри присяжных основана на модели, созданной для объяснения преимуществ принципа большинства. В соответствии с ней присяжные принимают бинарное решение о виновности или невиновности подсудимого. Каждый присяжный в основном выносит правильное решение. Чтобы применить эту теорему к совокупности моделей, а не членов жюри присяжных, мы интерпретируем принятие решения каждым присяжным как классификацию согласно той или иной модели. В качестве классов могут выступать действия (купить или продать) или прогнозы (победителем станет представитель демократической или республиканской партии). Далее теорема указывает на то, что конструирование множества моделей и применение принципа большинства обеспечит более высокий уровень точности, чем при использовании одной из моделей данного множества. Модель опирается на концепцию состояния мира — полное описание всей значимой информации. Для жюри присяжных состояние мира складывается из доказательств, представленных в суде. Для моделей, которые оценивают социальный вклад благотворительного проекта, оно может представлять команду проекта, организационную структуру, план проведения мероприятий и особенности проблемы или ситуации, которую должен решить проект.
Теорема Кондорсе о жюри присяжных
Каждый из нечетного количества людей (моделей) классифицирует неизвестное состояние мира как истинное или ложное. Каждый человек (модель) классифицирует правильно с вероятностью 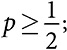 вероятность того, что другой человек (модель) выполнит правильную классификацию, статистически независима от правильности классификации любого другого человека (модели).
вероятность того, что другой человек (модель) выполнит правильную классификацию, статистически независима от правильности классификации любого другого человека (модели).
Теорема Кондорсе о жюри присяжных: большинство голосов обеспечивают правильную классификацию с более высокой вероятностью, чем любой отдельный человек (модель), а по мере увеличения количества членов жюри (моделей) точность решения, принятого большинством, приближается к 100 процентам.
Эколог Ричард Левинс объясняет, как применить логику этой теоремы к многомодельному подходу: «Мы пытаемся решить одну и ту же задачу с помощью ряда альтернативных моделей с разными упрощениями, но общим биологическим предположением. В таком случае, если эти модели, несмотря на различие исходных предположений, приводят к аналогичным результатам, мы имеем то, что можно назвать устойчивой теоремой, относительно свободной от деталей модели. Следовательно, истина находится на пересечении независимых случаев лжи» . Обратите внимание, что здесь Левинс рассчитывает на единство классификации. Когда многие модели дают одну и ту же классификацию, наша уверенность должна повыситься.
Следующая теорема, о прогнозе разнообразия, применима к моделям, которые делают численные прогнозы или оценки. Она количественно оценивает влияние точности моделей и их разнообразия на точность их среднего , .
Теорема о прогнозе разнообразия
Погрешность множества моделей = средняя погрешность модели — разнообразие прогнозов моделей
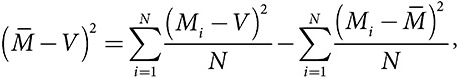
где Mi — это прогноз i-й модели, 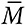 — среднее значений моделей, а V — истинное значение.
— среднее значений моделей, а V — истинное значение.
Теорема о прогнозе разнообразия описывает математическое тождество. Нам не нужно его проверять — оно всегда справедливо. Вот пример. Две модели прогнозируют количество «Оскаров», которые присудят одному из фильмов. Одна модель предсказывает два «Оскара», а другая — восемь. Среднее значение прогнозов двух моделей (прогноз на основе множества моделей) равно пяти. Если на самом деле фильм получит четыре «Оскара», то квадратичная погрешность прогноза первой модели будет равна 4 (2 в квадрате), второй — 16 (4 в квадрате), а множества моделей — 1. Разнообразие прогностических моделей составляет 9, поскольку прогноз каждой модели отличается от среднего прогноза на 3. В таком случае теорему о прогнозе разнообразия можно записать так: 1 (погрешность множества моделей) = 10 (средняя погрешность моделей) – 9 (разнообразие прогностических моделей).
Логика этой теоремы опирается на противоположные (плюсы и минусы) взаимоисключающие типы погрешностей. Если одна модель прогнозирует слишком высокое значение, а другая — слишком низкое, то эти модели демонстрируют разнообразие прогнозов. Обе погрешности исключают друг друга, а среднее значений моделей будет точнее, чем значение каждой модели в отдельности. Даже если оба прогнозируемых значения слишком высоки, ошибка среднего этих прогнозов все равно будет не больше, чем средняя двух завышенных прогнозов.
Из теоремы не следует, что совокупность различных моделей обеспечивает точную картину. Если всем моделям свойственна общая систематическая ошибка, то и среднее тоже будет ее содержать. Данная теорема подразумевает, что любая совокупность различных моделей (или людей) будет точнее, чем средний член этой совокупности — феномен, известный как «мудрость толпы». Этот математический факт объясняет эффективность ансамблевых методов в информатике, которые выводят среднее множества классификаций, а также то, что люди, использующие в рассуждениях множество моделей и концептуальных схем, делают более точные прогнозы по сравнению с теми, кто ориентируется лишь на отдельные модели. Любой однобокий взгляд на мир упускает важные детали и оставляет белые пятна. У таких людей меньше шансов предвидеть крупные события, такие как крах рынка или арабская весна 2011 года .
Обе теоремы приводят убедительные аргументы в пользу применения множества моделей, по крайней мере в контексте прогнозирования. Однако порой эти аргументы излишне убедительны. Теорема Кондорсе подразумевает, что при достаточном количестве моделей мы бы практически никогда не ошибались, а теорема о прогнозе — что формирование разнопланового множества умеренно точных моделей прогнозирования позволило бы нам свести погрешность множества моделей практически к нулю. Однако, как мы увидим далее, наша способность строить множество разноплановых моделей не беспредельна.
МОДЕЛИ КАТЕГОРИЗАЦИИ
Чтобы объяснить, почему обе теоремы могут преувеличивать аргументы в пользу многомодельного подхода, прибегнем к моделям категоризации, которые обеспечивают микрообоснования теоремы Кондорсе о жюри присяжных и делят состояния мира на непересекающиеся блоки. Эти модели восходят к эпохе античности. В своем труде The Categories Аристотель выделил десять атрибутов, в том числе такие как субстанция, количество, место и положение, которые использовал для разделения мира на категории. Каждая комбинация этих атрибутов образует отдельную категорию.
Мы используем категории каждый раз, когда употребляем нарицательное существительное. «Брюки» — это категория, так же как «собаки», «ложки», «камины» и «летние каникулы». Нам свойственно использовать категории в качестве руководства к действию. Мы распределяем рестораны по национальному признаку (итальянские, французские, турецкие или корейские), чтобы выбрать, где пообедать. Классифицируем акции по отношению рыночной цены акции к чистой прибыли на одну акцию и продаем малодоходные акции. Используем категории для объяснения тех или иных явлений — как в случае с утверждением, что численность населения Аризоны возросла, потому что в этом штате благоприятные погодные условия. Кроме того, категории применяются для прогнозирования: мы можем предсказать, что у кандидата на государственную должность, имеющего военный опыт, более высокие шансы на победу.
Мы можем интерпретировать вклад моделей категоризации в рамках иерархии мудрости. Объекты образуют данные. Группирование объектов по категориям порождает информацию. Определение оценок по категориям требует знаний. Для критического анализа теоремы Кондорсе мы полагаемся на модель бинарной категоризации, которая делит объекты или состояния мира на две категории — «виновен» и «невиновен». Основная идея состоит в том, что количество соответствующих атрибутов ограничивает число отдельных вариантов категоризации, а значит, и число полезных моделей.
Модели категоризации
Существует множество объектов или состояний мира, каждое из которых определяется множеством атрибутов и имеет то или иное значение. Модель категоризации М делит эти объекты или состояния на конечное множество категорий {S1, S2, …, Sn} на основе атрибутов объекта и присваивает оценки {M1, M2, …, Mn} каждой категории.
Представьте, что у нас есть сто заявок на получение студенческого кредита, половина из которых были погашены, а половина — нет. По каждому кредиту нам известны две детали: превышал ли его размер 50 000 долларов и специализировался ли его получатель в инженерном деле или в гуманитарных науках. Это и есть два атрибута. С их помощью мы можем выделить четыре типа кредитов: крупные кредиты студентам со специализацией «инженерное дело», мелкие кредиты студентам со специализацией «инженерное дело», крупные кредиты студентам со специализацией «гуманитарные науки» и мелкие кредиты студентам со специализацией «гуманитарные науки».
Модель бинарной категоризации классифицирует каждый из четырех типов кредитов как выплаченный или невыплаченный. Одна модель может классифицировать мелкие кредиты как выплаченные, а крупные как невыплаченные. Другая может классифицировать кредиты студентам со специализацией «инженерное дело» как погашенные, а студентам со специализацией «гуманитарные науки» как непогашенные. Вполне вероятно, что каждая из этих моделей может быть правильной более чем в половине случаев и что эти две модели могут быть практически независимы друг от друга. Проблема возникает при попытке создать больше моделей. Существуют только шестнадцать уникальных моделей, которые соотносят четыре категории с двумя возможными исходами. Две классифицируют все кредиты как выплаченные или невыплаченные, у каждой из оставшихся четырнадцати есть полная противоположность. Всякий раз, когда модель обеспечивает правильную классификацию, ее противоположный вариант дает неправильную классификацию. Таким образом, из четырнадцати возможных моделей максимум семь могут быть правильными более чем в половине случаев. И если та или иная модель окажется правильной ровно в половине случаев, то же произойдет и с ее противоположностью.
Размерность наших данных ограничивает количество моделей, которые мы можем создать. У нас может быть максимум семь моделей. Мы не можем построить одиннадцать независимых моделей, не говоря уже о семидесяти семи. Даже если бы у нас были данные с более высокой размерностью (например, если бы мы знали возраст, средний балл, доход, семейное положение и адрес получателей кредита), категоризация, основанная на этих атрибутах, должна обеспечивать точные прогнозы. Каждое подмножество атрибутов должно быть релевантным тому, погашен ли кредит, и не связанным с другими атрибутами. В обоих случаях речь идет о сильных предположениях. Например, если между адресом, семейным положением и доходом наблюдается корреляция, то модели, в которых эти атрибуты поменяны местами, тоже должны коррелировать . В случае строгой вероятностной модели независимость кажется обоснованной: разные модели порождают разные ошибки. Объяснение этой логики с помощью моделей категоризации позволяет осознать сложность построения множества независимых моделей.
Попытки формирования совокупности разноплановых, точных моделей сопряжены с аналогичной проблемой. Предположим, нам нужно создать ансамбль моделей категоризации, прогнозирующих уровень безработицы в пятистах городах среднего размера. Точная модель должна разделить города на категории таким образом, чтобы в рамках одной категории в них наблюдался схожий уровень безработицы. Кроме того, модель должна точно прогнозировать безработицу в каждой категории. Для того чтобы две модели обеспечивали разные прогнозы, они должны по-разному делить города на категории, по-разному составлять прогнозы, или и то и другое. Хотя эти два критерия не противоречат друг другу, могут возникнуть трудности с их удовлетворением. Если один вариант категоризации основан на среднем уровне образования, а другой — на среднем уровне дохода, они могут обеспечивать разбиение на аналогичные категории. Тогда обе модели будут точными, но не разнообразными. Формирование двадцати шести категорий с использованием первой буквы названия каждого города обеспечит разноплановую категоризацию, но, по всей вероятности, не позволит создать точную модель. Поэтому здесь снова напрашивается вывод, что на практике количество элементов «множества» обычно ближе к пяти, чем к пятидесяти.
Результаты эмпирических исследований прогнозирования согласуются с этим выводом. Хотя увеличение числа моделей повышает уровень точности (как и должно быть согласно теоремам), после формирования группы моделей предельный вклад каждой из них снижается. В компании Google обнаружили, что привлечение одного интервьюера для оценки кандидатов на вакантную должность (вместо случайного выбора) повышает вероятность найма высококвалифицированного сотрудника с 50 до 74 процентов, привлечение второго интервьюера повышает эту вероятность до 81 процента, привлечение третьего интервьюера — до 84 процентов, а четвертого — до 86 процентов. Наличие двадцати интервьюеров повышает вероятность всего до 90 процентов с небольшим. Это указывает на ограничение предельного количества значимых способов оценки потенциального сотрудника.
Аналогичный вывод справедлив и при оценке десятков тысяч прогнозов экономистов в отношении безработицы, экономического роста и инфляции. В этом случае следует рассматривать экономистов как модели. Включение второго экономиста повышает точность прогноза примерно на 8 процентов, еще два экономиста повышают его на 12 процентов, а еще три — более чем на 15 процентов. Десять экономистов увеличивают точность прогноза примерно на 19 процентов. Кстати, прогноз лучшего экономиста всего на 9 процентов точнее, чем среднего, при условии, что вы знаете, какой экономист лучший. Таким образом, три произвольно выбранных экономиста эффективнее, чем один лучший . Еще одна причина использования нескольких средних экономистов, не полагаясь на одного, пусть в прошлом и лучшего, — изменчивость мира. Экономист, демонстрирующий сегодня самые высокие результаты, завтра может стать середняком. Аналогичная логика объясняет, почему Федеральная система США полагается на совокупность экономических моделей, а не на одну модель: как правило, множество моделей обеспечивают более высокий средний результат, чем самая лучшая одиночная модель.
Урок должен быть очевиден: формирование множества разноплановых, точных моделей позволяет нам составлять очень точные прогнозы и оценки и выбирать правильные действия. Теоремы обосновывают логику многомодельного мышления. Чего они не делают и не могут сделать, так это построить множество моделей, удовлетворяющих их исходным предположениям. На практике мы можем обнаружить, что имеем возможность создать три-пять хороших моделей. И если так, то это здорово! Нам нужно только вернуться к предыдущему абзацу: включение второй модели обеспечивает улучшение на 8 процентов, а третьей — уже на 15 процентов. Учтите, что вторая и третья модели не обязательно должны быть лучше первой. Они могут быть хуже. Однако если эти модели чуть менее точны, но отличаются в категорийном смысле, их следует включить в совокупность.
ОДНА БОЛЬШАЯ МОДЕЛЬ И ВОПРОС О СТЕПЕНИ ДЕТАЛИЗАЦИИ
Многие модели работают в теории и на практике. Но это не значит, что многомодельный подход всегда верен. Иногда лучше разработать одну большую модель. В этом разделе мы проанализируем, когда целесообразнее использовать каждый из подходов и попутно рассмотрим вопрос о степени детализации, то есть о том, насколько детальным должно быть разделение данных.
Для того чтобы ответить на первый вопрос (использовать одну большую модель или множество маленьких), вспомните об областях применения моделей: рассуждение, объяснение, разработка, коммуникация, действие, прогнозирование и исследование. Четыре из них (рассуждение, объяснение, коммуникация и исследование) требуют упрощения, благодаря чему мы можем использовать логику, позволяющую объяснять те или иные явления, распространять свои идеи и исследовать возможности.
Вспомните теорему Кондорсе о жюри присяжных. С ее помощью мы смогли раскрыть логику, объяснить, почему подход с использованием множества моделей с большой вероятностью обеспечит правильный результат, и сделать выводы. Если бы мы включили в модель жюри присяжных типы личности и представили доказательства в виде одномерного массива слов, мы заблудились бы в лесу деталей. Борхес рассуждает об этом в своем эссе о науке, рассказывая о составителях карт, стремившихся к чрезмерной детализации: «Коллегия картографов создала карту империи, которая была размером с империю и совпадала с ней до единой точки. Потомки, не столь преданные изучению картографии, сочли эту пространную карту бесполезной».
Модели с высоким уровнем точности будут полезны и для трех оставшихся областей применения моделей, таких как прогнозирование, разработка и действие. При наличии БОЛЬШИХ данных мы должны их использовать. Эмпирическое правило звучит так: чем больше у нас данных, тем детализированнее должна быть модель. Это можно продемонстрировать на примере применения моделей категоризации для структурирования мышления. Допустим, нам нужно построить модель для объяснения вариации во множестве данных. Для создания контекста предположим, что у нас есть огромный массив данных сети продуктовых магазинов, содержащий подробную информацию о ежемесячных расходах нескольких миллионов домохозяйств на продукты питания. По объему расходов они разнятся, что мы измеряем как вариацию — сумму квадратов разности между величиной расходов каждого домохозяйства и средним объемом расходов по всем домохозяйствам. Если средний объем расходов составляет 500 долларов в месяц, а семья тратит 520 долларов, она вносит вклад в общую вариацию, равный 400, или 20 в квадрате.
Если общая вариация составляет 1 миллиард долларов, а модель объясняет 800 миллионов этой вариации, то ее показатель R2 составляет 0,8. Величина объясненной вариации соответствует тому, насколько данная модель улучшает оценку среднего значения. Если оценка, полученная с помощью модели, указывает, что домохозяйство потратит 600 долларов, и оно действительно тратит 600 долларов, то данная модель объясняет все 10 000, которые это домохозяйство вносит в общую вариацию. Если семья потратила 800 долларов, а согласно модели должна была потратить 700 долларов, тогда то, что было вкладом в общую вариацию 90 000 ((800 – 500)2), теперь составляет всего 10 000 ((800 – 700)2). Таким образом, данная модель объясняет 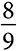 вариации.
вариации.
R2: процент объясненной дисперсии (коэффициент детерминации)
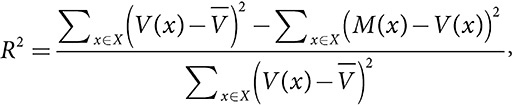
где V(x) — это значение x на множестве X, 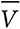 — среднее значение, а M(x) — оценка модели.
— среднее значение, а M(x) — оценка модели.
В данном контексте модель категоризации делит домохозяйства на категории и определяет значение по каждой. Более детализированная модель обеспечивает создание большего числа категорий. Это может потребовать анализа большего количества атрибутов домохозяйств. Увеличение числа категорий позволяет объяснить большую долю вариации, но мы можем зайти слишком далеко. Последовав примеру картографов Борхеса и отнеся каждое домохозяйство к отдельной категории, мы сможем объяснить всю вариацию. Но такое объяснение, как и карта в натуральную величину, не принесет особой пользы.
Создание избыточного количества категорий приводит к чрезмерной подгонке данных, а она препятствует прогнозированию будущих событий. Предположим, мы хотим использовать данные о покупках продуктов за прошлый месяц для прогнозирования данных за нынешний месяц. Ежемесячные расходы домохозяйств отличаются. Модель, которая относит каждое домохозяйство к его собственной категории, предскажет, что оно потратит столько же, сколько и в прошлом месяце. Но это будет не очень хороший прогноз, учитывая ежемесячные колебания расходов. Отнеся домохозяйства к категории им подобных, мы сможем использовать средний объем расходов на продукты аналогичных домохозяйств для создания более точного прогноза.
Для этого мы будем рассматривать ежемесячный объем расходов каждого домохозяйства как одно из значений распределения (о распределениях рассказывается в ). У этого распределения есть среднее значение и дисперсия. Задача построения модели категоризации — создать категории на основе атрибутов таким образом, чтобы у домохозяйств в рамках одной категории были близкие средние значения. Тогда объем расходов одной семьи за первый месяц позволит определить объем расходов другой семьи за второй месяц. Однако ни один вариант категоризации не может быть идеальным. Средний объем расходов домохозяйств, входящих в одну категорию, будет немного отличаться. Мы называем это погрешностью категоризации.
Увеличивая категории, мы увеличиваем и погрешность категоризации, поскольку возрастает вероятность отнесения к одной категории домохозяйств с разными средними значениями. Впрочем, более крупные категории основаны на большем количестве данных, а значит, оценки среднего в каждой категории будут точнее (см. ). Погрешность, возникающая из-за неправильной оценки среднего, называется погрешностью оценки. По мере увеличения категорий погрешность оценки уменьшается. Включение одного или даже десяти домохозяйств в одну категорию не позволит получить точную оценку среднего, если они будут существенно разниться по ежемесячному объему расходов. Тысяча домохозяйств в одной категории обеспечат такую оценку.
Итак, мы получили важный интуитивный вывод: увеличение количества категорий влечет за собой погрешность категоризации в связи с отнесением домохозяйств с разными средними значениями к одной категории. Статистики называют это систематической ошибкой модели. Вместе с тем создание большего количества категорий увеличивает погрешность оценки среднего в пределах каждой категории. Статистики называют это увеличением дисперсии среднего значения. Компромиссное решение в отношении того, сколько категорий необходимо выделить, можно формально описать с помощью теоремы о декомпозиции погрешности модели. Статистики называют этот результат компромиссом между смещением и дисперсией.
Теорема о декомпозиции погрешности модели
Компромисс между смещением и дисперсией
Погрешность модели = погрешность категоризации + погрешность оценки
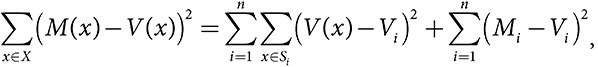
где M(x) и Mi — это значения модели для элемента данных x в категории Si, а V(x) и Vi — истинные значения , .
ИСПОЛЬЗОВАНИЕ ОДНОЙ МОДЕЛИ ВО МНОГИХ ОБЛАСТЯХ
Для изучения моделей требуется время, усилия и широта охвата. Снизить эти требования помогает подход «использование одной модели во многих областях». Мы предлагаем освоить небольшое количество гибких моделей и креативно их применять. Мы используем модель из области эпидемиологии, чтобы понять процесс распространения семян кукурузы, сети Facebook, преступности и поп-музыки. Мы применяем модель распространения сигнала к рекламе, браку, оперению павлинов и страховым взносам. Кроме того, мы используем модель пересеченного адаптивного ландшафта, чтобы объяснить, почему у людей нет дыхала. Безусловно, не каждая модель применима в любом контексте, но большинство моделей достаточно гибкие. Мы выигрываем даже в случае неудачи, поскольку попытки креативного применения моделей позволяют установить их пределы. К тому же это интересно.
Подход «использование одной модели во многих областях» сравнительно новый. В прошлом модели относились к конкретным дисциплинам. У экономистов были модели спроса и предложения, монопольной конкуренции и экономического роста; у политологов — модели предвыборной борьбы; у экологов — модели видообразования и репликации, а у физиков модели, описывающие законы движения. Все эти модели разрабатывались для определенных целей. Никто не применял модель из физики к экономике или модель из экономики к головному мозгу, как никто не стал бы использовать швейную машинку для ремонта протекающей трубы.
Выход моделей за рамки своих дисциплин и использование одной модели в нескольких областях позволило добиться значительных успехов. Пол Самуэльсон переосмыслил модели из физики для объяснения нюансов рыночного равновесия. Энтони Даунс использовал модель конкуренции между продавцами мороженого на пляже для объяснения позиционирования кандидатов на политические должности, ведущих идеологическую борьбу. Социологи применили модели взаимодействия частиц для объяснения ловушек бедности, колебаний уровня преступности и даже экономического роста в разных странах. А экономисты использовали модели саморегулирования, основанного на экономических принципах, чтобы понять, как функционирует головной мозг .
ИСПОЛЬЗОВАНИЕ ОДНОЙ МОДЕЛИ ВО МНОГИХ ОБЛАСТЯХ: ПРИМЕР — ВЫСОКИЕ СТЕПЕНИ XN
Креативное применение моделей требует практики. Для того чтобы получить предварительное представление о потенциале подхода использования одной модели во многих областях, возьмем знакомую формулу возведения переменной в степень, XN, и используем ее в качестве модели. Кода степень равна 2, формула дает площадь квадрата со стороной Х, а когда 3 — объем куба со стороной Х. В случае более высоких степеней формула отражает геометрическое расширение или геометрический спад.
Супертанкеры. Наш первый пример применения этого подхода — супертанкер в виде прямоугольного параллелепипеда, длина которого в восемь раз превышает его высоту и ширину, обозначенные символом S. Как показано на рис. 3.1, площадь поверхности супертанкера равна 34S2, а объем — 8S3. Стоимость строительства супертанкера зависит прежде всего от площади его поверхности, которая определяет количество используемой стали. Размер дохода от эксплуатации супертанкера зависит от его объема. Вычисление отношения объема к площади поверхности по формуле 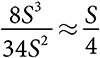 показывает линейное повышение рентабельности (которая пропорциональна объему) за счет увеличения размера.
показывает линейное повышение рентабельности (которая пропорциональна объему) за счет увеличения размера.
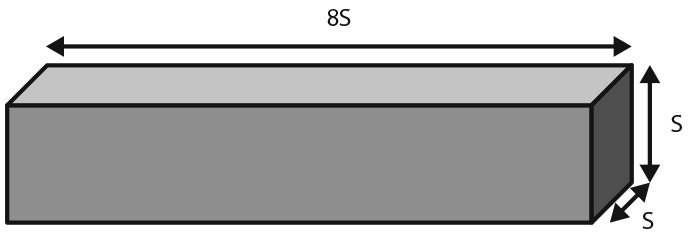
Рис. 3.1. Супертанкер в виде прямоугольного параллелепипеда: площадь поверхности = 34S2, объем = 8S3
Судоходный магнат Ставрос Ниархос, знавший об этом соотношении, построил первые современные супертанкеры и заработал миллиарды в период восстановления после Второй мировой войны. Чтобы вы могли получить некоторое представление о масштабах, давайте сравним: длина нефтяного танкера T2, который использовался во время Второй мировой войны, составляла 152,4 метра, высота 7,62 метра и ширина 15,24 метра. У современных супертанкеров, таких как Knock Nevis, следующие размеры: длина 457,2 метра, высота 24,38 метра и ширина 54,87 метра. Представьте, что башня Willis (Sears) в Чикаго легла на бок и плывет по озеру Мичиган. Супертанкер Knock Nevis похож на танкер Т2, но увеличен в три с небольшим раза. Площадь поверхности Knock Nevis в десять раз превышает площадь поверхности Т2, а объем в тридцать раз больше. Возникает вопрос, почему супертанкеры не бывают еще крупнее? Ответ прост: танкеры должны проходить через узкий Суэцкий канал; Knock Nevis буквально протискивается через него, оставляя всего несколько десятков сантиметров с каждой стороны .
Индекс массы тела. Индекс массы тела (body mass index, BMI) используется в медицине для определения весовых категорий. Разработанный в Англии, BMI равен отношению веса человека (в килограммах) к квадрату его роста в метрах . При постоянном росте индекс массы тела находится в линейной зависимости от веса. Если один человек весит на 20 процентов больше, чем другой человек того же роста, BMI первого человека будет на 20 процентов больше.
Сначала мы используем нашу модель для приближенного представления человека в виде идеального куба, состоящего из жира, мышц и костей. Обозначим символом M вес одного кубического метра нашего кубического человека. Вес человека-куба равен произведению его объема на вес кубического метра, или H3 · M, а BMI равен H · M. Данная модель указывает на два недостатка: BMI увеличивается линейно в зависимости от роста, а учитывая, что мышцы тяжелее жира, у людей, которые находятся в хорошей физической форме, более высокое значение M, а значит, и более высокий индекс массы тела. Рост не должен быть связан с ожирением, а мускулатура — вовсе не тучность, а ее противоположность. Эти недостатки сохраняются и в более реалистичной модели. Если мы сделаем глубину (толщину от груди до спины) и ширину человека пропорциональной росту посредством введения параметров d и w, то индекс массы тела можно будет записать так: 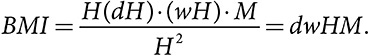 BMI многих звезд NBA и других спортсменов относит их к категории людей с избыточным весом (BMI > 25), как и многих лучших мужчин-десятиборцев мира . Учитывая, что высокий BMI бывает даже у людей среднего роста, находящихся в хорошей физической форме, не стоит удивляться тому, что согласно метаанализу результатов примерно сотни исследований с размером смешанной выборки, исчисляемым миллионами, дольше всего живут люди со слегка избыточным весом .
BMI многих звезд NBA и других спортсменов относит их к категории людей с избыточным весом (BMI > 25), как и многих лучших мужчин-десятиборцев мира . Учитывая, что высокий BMI бывает даже у людей среднего роста, находящихся в хорошей физической форме, не стоит удивляться тому, что согласно метаанализу результатов примерно сотни исследований с размером смешанной выборки, исчисляемым миллионами, дольше всего живут люди со слегка избыточным весом .
Уровень метаболизма. Теперь применим нашу модель для прогнозирования обратной зависимости между размером животного и уровнем его метаболизма. У каждого живого существа происходит обмен веществ — повторяющаяся последовательность химических реакций, которые расщепляют органические вещества и преобразуют их в энергию. Скорость обмена веществ в организме, или уровень метаболизма, измеряемый в калориях, эквивалентен количеству энергии, необходимой для поддержания жизнедеятельности. Если мы сконструируем кубические модели мыши и слона, то, как показывает рис. 3.2, у куба меньшего размера отношение площади поверхности к объему будет гораздо больше.
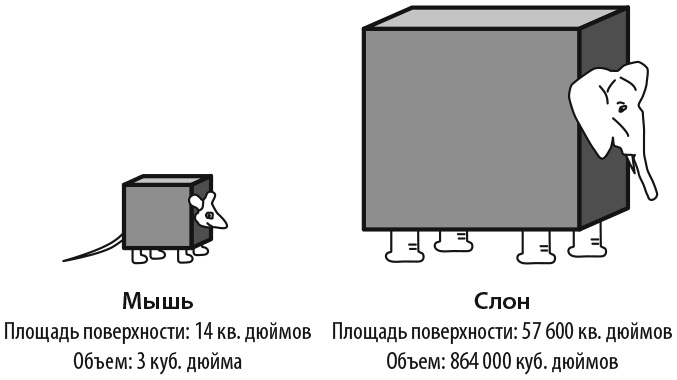
Рис. 3.2. Взрывающийся слон
Мы можем представить мышь и слона в качестве модели, состоящей из ячеек объемом 1 кубический дюйм, каждая из которых обладает метаболизмом. Эти метаболические реакции создают тепло, которое должно рассеиваться через поверхность животного. Площадь поверхности мыши равна 14 квадратных дюймов, а объем — 3 кубических дюйма, а значит, отношение площади поверхности к объему составляет 5:1 . На каждую ячейку объема в один кубический дюйм у мыши есть пять квадратных дюймов площади поверхности, через которую она может рассеивать тепло. Площадь поверхности каждой теплообразующей ячейки слона равна всего одной пятнадцатой квадратного дюйма. Следовательно, мышь может рассеивать тепло в семьдесят пять раз быстрее слона.
Для того чтобы у обоих животных была одинаковая внутренняя температура, у слона должен быть более медленный метаболизм. Слону с метаболизмом мыши понадобилось бы 15 000 фунтов (около 7 тонн) пищи в день. Кроме того, ячейки слона выделяли бы слишком много тепла, чтобы его можно было рассеивать через шкуру животного. В итоге слон начал бы тлеть, а затем взорвался бы. Однако слоны не взрываются, потому что уровень их метаболизма примерно в двадцать раз ниже, чем у мышей. Данная модель прогнозирует не скорость изменения уровня метаболизма в зависимости от размера, а только направление. Более сложные модели могут объяснить законы масштабирования .
Доля женщин-руководителей. В последнем примере мы увеличим показатель степени в формуле и используем данную модель для объяснения того, почему так мало женщин становятся руководителями компаний. В 2016 году менее чем в 5 процентах компаний из списка Fortune 500 должность СЕО занимали женщины. Для того чтобы стать СЕО, человек должен получить ряд повышений. Мы можем представить шансы на повышение как вероятностные события: у человека есть определенная вероятность получить повышение. Кроме того, будем исходить из предположения, что для назначения на должность СЕО человек должен продвигаться по служебной лестнице при каждом удобном случае. Возьмем пятнадцать повышений в качестве эталона, поскольку это соответствует повышению каждые два года за тридцатилетний путь к креслу СЕО. Факты свидетельствуют о небольшом смещении в пользу мужчин, что мы можем представить как наличие у мужчин более высокой вероятности продвижения по службе . Обозначим это как вероятность повышения мужчин PM, которая немного выше вероятности продвижения женщин PW. Если оценить эти вероятности как 50 и 40 процентов соответственно, то у мужчины будет примерно в 30 раз больше шансов стать СЕО, чем у женщины . Данная модель показывает, как постепенно накапливаются скромные смещения. Десятипроцентная разница в темпах продвижения по карьерной лестнице в итоге превращается в 30-кратное отличие. Эта же модель объясняет, почему гораздо более высокая доля (25 процентов) президентов колледжей и университетов — женщины. В колледжах и университетах меньше административных уровней, чем в компаниях из списка Fortune 500. Профессор может стать президентом всего за три повышения: заведующий кафедрой, декан, а затем президент. На трех уровнях накапливается меньшее смещение. Следовательно, более значительная доля женщин-президентов колледжей и университетов не означает, что в учебных заведениях уровень эгалитарности по сравнению с корпорациями выше.
РЕЗЮМЕ
Итак, в начале главы мы заложили логические основы применения одной модели во многих областях, воспользовавшись теоремой Кондорсе о жюри присяжных и теоремой о прогнозе разнообразия, а затем с помощью моделей категоризации показали пределы многообразия моделей. Мы выяснили, какое количество моделей может усилить нашу способность прогнозировать, действовать, разрабатывать и так далее, и, кроме того, поняли, что найти много разноплановых моделей не так просто. Иначе мы бы составляли прогнозы с почти идеальной точностью, что, как мы знаем, нереально. Тем не менее наша задача по-прежнему состоит в построении как можно большего числа полезных, разноплановых моделей.
В следующих главах представлен базовый набор моделей, описывающих разные аспекты мира. Они исходят из разных предположений о причинно-следственных связях и благодаря многообразию создают условия для продуктивного многомодельного мышления. Акцентируясь на отдельных аспектах более сложного целого, каждая модель вносит свой вклад. Кроме того, каждая модель может входить в состав еще более эффективного ансамбля моделей.
Как отмечалось выше, многомодельное мышление требует знания более чем одной модели. Однако это не означает, что нам нужно знать огромное количество моделей, учитывая возможность применения каждой модели во многих областях. Это не всегда будет просто. Успешное использование одной модели во многих областях зависит от креативной модификации исходных предположений и выстраивания необычных аналогий для применения модели в новом контексте. Таким образом, чтобы научиться многомодельному мышлению, необходимо нечто большее, чем просто знание математики; для этого нужен креативный подход, о чем свидетельствуют примеры применения модели куба.
Пакетирование и множество моделей
Нередко мы подбираем модель так, чтобы она соответствовала выборке из имеющегося набора данных, а затем тестируем ее на оставшихся данных. В других случаях мы приспосабливаем модель к существующим данным и используем для прогнозирования будущих данных. Моделирование такого типа создает противоречие: чем больше параметров мы включаем в модель, тем лучше подбираем данные и тем выше становится риск чрезмерной подгонки (переобучения). Хорошее соответствие не всегда дает хорошую модель. Физик Фримен Дайсон рассказывает о реакции Энрико Ферми на одно из исследований, в котором была задействована исключительно точно подобранная модель. «В отчаянии я спросил Ферми, разве его не впечатлило соответствие между нашими расчетными показателями и его результатами измерений. Он спросил в ответ: “Сколько произвольных параметров вы использовали в своих вычислениях?” Я подумал немного о наших процедурах исключения и ответил: “Четыре”. Он сказал: “Помню, как мой друг Джонни фон Нейман говорил, что с четырьмя параметрами он может описать слона, а с пятью — заставить его махать хоботом”. На этом разговор закончился» .
Оценки, используемые для того, чтобы «заставить слона махать хоботом», очень часто включают в себя члены высшего порядка — квадраты, кубы и четвертые степени. Это создает риск крупных ошибок, поскольку члены высшего порядка усиливают соответствующие признаки. 10 в два раза больше 5, тогда как 104 уже в 16 раз больше 54. На представленном ниже рисунке показан пример переобучения.
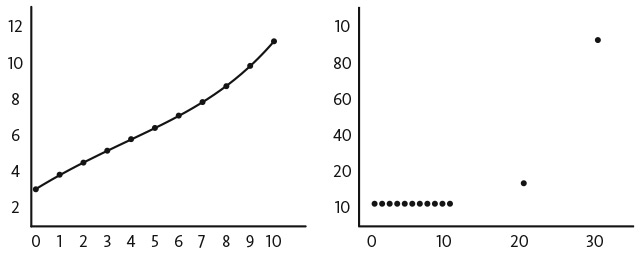
Переобучение и вневыборочная ошибка
На графике слева отображены (гипотетические) данные о продажах в компании по производству 3D-принтеров в зависимости от среднего количества визитов сотрудников отдела продаж на места за месяц. На графике представлено нелинейное наилучшее соответствие, включающее нелинейные члены вплоть до пятой степени. На графике справа показано, что данная модель прогнозирует продажу 100 принтеров, если количество визитов торговых агентов достигнет 30. Этот прогноз не может быть правильным, если клиенты покупают максимум по одному 3D-принтеру.
Чтобы предотвратить чрезмерную подгонку модели, мы могли бы избегать использования членов высшего порядка. Более сложное решение, известное как бутстрэп-агрегирование, или пакетирование, позволяет сконструировать множество моделей. Для выполнения бутстрэп-анализа набора данных мы создаем несколько наборов данных одинакового размера путем случайного выбора элементов данных из исходных данных с их последующим возвратом — после извлечения того или иного элемента данных мы возвращаем его назад, чтобы можно было выбрать его снова. Этот метод позволяет получить совокупность одинаковых по размеру наборов данных, каждый из которых содержит множество копий определенных элементов данных и ни одной копии других элементов данных.
Далее мы подбираем (нелинейные) модели к каждому набору данных и в итоге получаем множество моделей , которые затем можем отобразить в одной системе координат, получив при этом спагетти-график (см. рис. ниже). Темная линия показывает среднее для различных моделей.
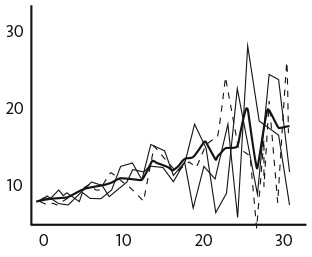
Бутстрэппинг и спагетти-график
Пакетирование позволяет обнаружить устойчивые нелинейные эффекты, поскольку они проявляются во многих случайных выборках, и при этом избежать подгонки моделей к специфическим закономерностям в любом отдельно взятом наборе данных. Обеспечивая многообразие посредством случайных выборок и усреднение множества моделей, пакетирование использует логику, лежащую в основе теоремы о прогнозе разнообразия. Такой подход позволяет создать разноплановые модели, среднее которых, как мы знаем, гораздо точнее, чем сами модели.

