Почти век назад в физике был сделан ряд экспериментальных открытий, требовавших изменения нашего мировоззрения. То, что обнаруживалось в этих экспериментах, представляло собой, по словам философа Томаса Куна, аномалии, которые не могла объяснить классическая физика. Эти аномалии открывали путь к революции в научной мысли.

Представьте себе, что вы — физик на пороге нового столетия. Одна из аномалий, которые хотите понять вы и ваши коллеги, касается того, как нагретые тела испускают излучение. Будучи физиком ньютоновской школы, вы считаете, что вселенная — это классическая машина, состоящая из частей, ведущих себя в соответствии с законами ньютоновской механики, которые почти все полностью известны. Вы верите, что, располагая всей информацией о частях и справившись с немногими оставшимися трудностями в отношении законов, вы сможете навсегда предсказать будущее вселенной. Однако эти немногие оставшиеся трудности неприятны. Вы не готовы отвечать на вопросы, касающиеся, например, того, каков закон излучения нагретых тел.

Вообразите, что в то время как вы ломаете голову над этим вопросом, ваша жена удобно устроилась рядом с вами перед горящим камином.

Вы (бормоча): Я просто не могу этого понять.

Она: Передай мне орешки.

Вы (передавая орешки): Я просто не могу понять, почему мы сейчас не загораем.

Она (смеясь): Ну, это было бы мило. У нас могли бы даже быть основания пользоваться камином в летнее время.

Вы: Понимаешь, теория говорит, что излучение от камина должно быть так же богато ультрафиолетом, как солнечный свет. Но что делает именно солнечный свет, а не свет камина, богатым этими высокими частотами? Почему мы сейчас не загораем, принимая ультрафиолетовую ванну?

Она: Подожди, пожалуйста. Чтобы я могла слушать это серьезно, тебе придется чуть замедлить темп и объяснить. Что такое частота? Что такое ультрафиолет?

Вы: Извини. Частота — это число периодов в секунду. Это мера того, как быстро колеблется волна. Для света это означает цвет. Белый свет состоит из света разных частот, или цветов. Красный — это низкочастотный свет, а фиолетовый — высокочастотный свет. Если частота еще выше, то это невидимый черный цвет, который мы называем ультрафиолетовым.

Она: Ладно, значит, и свет от горящих дров, и свет от солнца должен содержать массу ультрафиолета. К сожалению, солнце подчиняется вашей теории, а горящие дрова — нет. Быть может, в горящих дровах есть нечто особенное...

Вы: В действительности, все еще хуже. Все источники света, а не только солнце или горящие дрова должны давать большие количества ультрафиолета.

Она: А, это уже становится интересно. Инфляция ультрафиолета вездесуща. Но разве за всякой инфляцией не следует спад? Разве не поется в песенке, что все поднимающееся должно падать? (Она начинает напевать без слов.)

Вы (раздражаясь): Но как?

Она (протягивая миску с орешками): Хочешь орешков, дорогой?

В конце XIX в. многие физики испытывали разочарование, пока один из них не нарушил общую тенденцию — это был Макс Планк из Германии. В 1900 г. Планк совершил смелый концептуальный прорыв, заявив, что старой теории необходим квантовый скачок (он заимствовал слово квант, означающее «количество», из латыни). Излучение света раскаленными телами — например, горящими дровами или солнцем — вызывается электронами, крохотными колеблющимися электрическими зарядами. Эти электроны поглощают энергию из нагретой среды, например камина, и затем испускают ее обратно в виде излучения. Эта часть старой физики была верной, но затем классическая физика предсказывала, что испускаемое излучение должно быть богато ультрафиолетом, чему противоречили наши наблюдения. Планк (весьма храбро) объявил, что проблему испускания разных количеств ультрафиолета можно решить, если допустить, что электроны испускают или поглощают энергию только определенными дискретными порциями, которые он назвал «квантами» энергии.

Чтобы понять смысл кванта энергии, рассмотрим такую аналогию. Сравните случай шарика, катящегося по лестнице, со случаем, когда он катится по наклонной плоскости (рис. 1), на наклонной плоскости может занимать любое положение, и его положение может меняться на любую величину. Таким образом, это модель непрерывности, представляющая то, как мы думаем в классической физике. По контрасту, шарик на лестнице может находиться только на той или иной ступени; его положение (и его энергия, которая связана с положением) «квантовано».

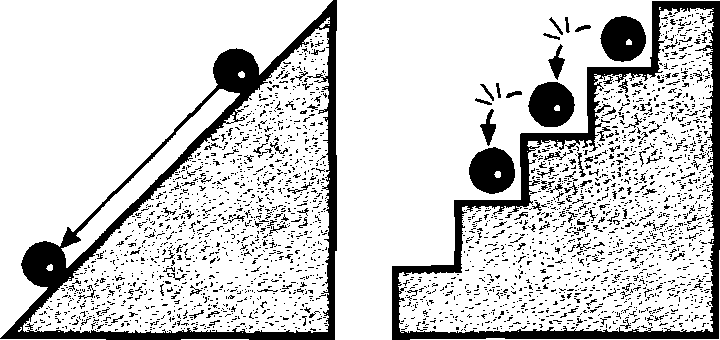
Рнс. 1. Квантовый скачок. На наклонной плоскости классическое движение шарика является непрерывным; на лестнице квантовой движение происходит в виде дискретных стадий (квантовых скачков)

Вы можете возразить — что происходит, когда шарик падает с одной ступени на другую? Разве во время своего спуска он не занимает промежуточные положения? Именно здесь проявляется необычность квантовой теории. Для шарика на лестнице ответ, очевидно, должен быть положительным, но для случая квантового шарика (атома или электрона) теория Планка дает отрицательный ответ. Квантовый шарик никогда не может быть обнаружен в любом промежуточном положении между двумя ступеньками; он находится либо на одной, либо на другой. Это — квантовая прерывистость.

Итак, почему вы не можете получить загар от огня дров в камине? Представьте себе маятник на ветру Обычно в такой ситуации маятник будет раскачиваться, даже если ветер не очень сильный. Предположите, однако, что маятник может поглощать энергию только дискретными порциями большой величины. Иными словами, это квантовый маятник. Что тогда? Ясно, что если только ветер не способен давать требуемое высокое нарастание энергии за один шаг, то маятник не будет двигаться. Поглощение небольших значений энергии не позволит ему накопить достаточно энергии для преодоления порога. Так и с колеблющимися электронами в камине. В результате небольших квантовых скачков возникает низкочастотное излучение, но для высокочастотного излучения требуются большие квантовые скачки. Большой квантовый скачок должен вызываться большим количеством энергии в среде, окружающей электрон; энергия дров, горяших в камине, просто недостаточно сильна, чтобы создавать условия для выделения большого количества голубого света, не говоря уже об ультрафиолете. Вот по какой причине нельзя загореть, сидя у камина.

Насколько известно, Планк был довольно традиционным ученым и с неохотой обнародовал свои идеи относительно квантов энергии. Он даже занимался своей математикой стоя, как в то время было принято в Германии. Ему не особенно нравились следствия его новаторской идеи; однако ученым, которым предстояло продвинуть революцию намного дальше, становилось ясно, что они указывают на совершенно новый способ понимания нашей физической реальности.

Одним из этих революционеров был Альберт Эйнштейн. В то время когда он опубликовал свою первую исследовательскую статью по квантовой теории, он работал клерком в патентном бюро в Цюрихе (1900). Подвергнув сомнению популярное в то время представление о волновой природе света, Эйнштейн выдвинул гипотезу, что свет существует в идее кванта — дискретного пучка энергии, — который мы теперь называем фотоном. Чем выше частота света, тем большую энергию имеет каждый пучок.

Еще большим революционером был датский физик Нильс Бор, который в 1913 г. использовал идею кванта света для формулировки гипотезы, согласно которой весь мир атома полон квантовых скачков. Нас всех учили, что атом похож на миниатюрную солнечную систему, что электроны вращаются вокруг ядра во многом подобно тому, как планеты вращаются вокруг Солнца. Возможно, вам будет интересно узнать, что эта модель, предложенная английским физиком Эрнстом Резерфордом, имела решающий недостаток, который устраняла работа Бора.

Представьте себе рой движущихся по орбитам спутников, которые довольно регулярно запускают с Земли с помощью космических ракет. Эти спутники существуют не вечно. Вследствие столкновения с земной атмосферой, они теряют энергию и замедляют свое движение. Их орбиты сужаются, и, в конечном счете, они падают на Землю (рис. 2).

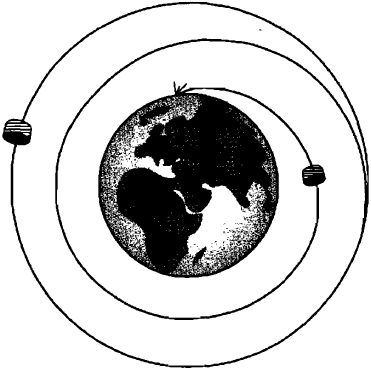
Рис. 2. Орбиты спутников, вращающихся вокруг Земли, неустойчивы. Так же ведут себя и орбиты электронов в модели атома Резерфорда

Согласно классической физике, электроны, окружающие атомное ядро, тоже должны были бы терять энергию вследствие непрерывного излучения света и в конце концов падать на ядро. Поэтому планетарная модель атома неустойчива. Однако Бор (который, предположительно, увидел планетарную систему атома во сне) создал устойчивую модель атома, применив идею квантового скачка.

Предположим, говорил Бор, что орбиты электронов дискретны, подобно квантам энергии Планка. Тогда орбиты можно представлять себе как образующие энергетическую лестницу (рис. 3). Они стационарны — величина их энергии остается неизменной. Находясь на этих квантованных орбитах, электроны не излучают света. Электрон испускает квант света, только когда перескакивает с орбиты с более высокой энергией на орбиту с более низкой (со ступени лестницы с более высокой энергией на более низкую ступень). Таким образом, если электрон находится на орбите с самой низкой энергией, у него нет более низкого уровня, куда бы он мог перескакивать. Эта конфигурация базового уровня устойчива, и у электрона нет никаких шансов упасть на ядро. Все физики встретили модель атома Бора вздохом облегчения.

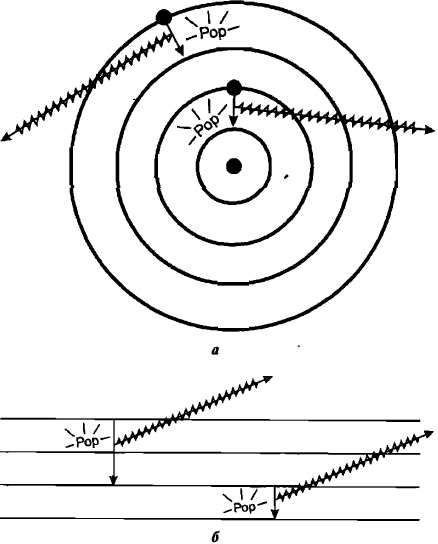
Рис. 3. Орбита Бора и квантовый скачок: а — квантованные орбиты Бора. Атомы испускают свет, когда электроны перескакивают с орбиты на орбиту; б — для квантовых скачков по энергетической лестнице нет нужды проходить через промежуточное пространство между ступенями

Бор отсек голову Гидре неустойчивости, но на ее месте вырастала другая. Согласно Бору, электрон никогда не может занимать никакое положение между орбитами; таким образом, совершая скачок, он должен каким-то образом непосредственно переходить на другую орбиту. Это не орбитальный прыжок через пространство, а что-то радикально новое. Хотя, возможно, было бы соблазнительно изображать скачок электрона как прыжок с одной ступеньки лестницы на другую, однако электрон совершает скачок, не пересекая пространство между ступеньками. Вместо этого он как будто исчезает на одной ступеньке, снова появляясь на другой — без какого бы то ни было непрерывного перехода. Больше того, нельзя сказать, куда он собирается перескакивать, если существует больше одной более низкой ступени, между которыми он может выбирать. Можно давать лишь вероятностные предсказания.

Возможно, вы заметили в квантовой концепции света кое-что странное. Говорить, что свет существует в виде квантов, фотонов, — значит утверждать, что свет состоит из частиц, подобных песчинкам. Однако такое утверждение во многом противоречит повседневному опыту, который мы получаем, имея дело со светом.

Представьте себе, например, что вы смотрите на отдаленный уличный фонарь через ткань матерчатого зонтика. Вы не увидите непрерывный поток света, проходящий насквозь, как следовало бы ожидать, если бы свет состоял из крохотных частиц (насыпьте песка в решето, и вы увидите, что я имею в виду). Вместо этого вы увидите узор из чередующихся темных и светлых каемок, который технически называется интерференционной картиной. Свет изгибается в нитях ткани и вокруг них, создавая картину, которую могут образовывать только волны. Таким образом, даже наш повседневный опыт показывает, что свет ведет себя как волна.

Тем не менее квантовая теория настаивает, что свет также ведет себя как пучок частиц, или фотонов. Наши глаза представляют собой такой замечательный инструмент, что мы можем сами наблюдать квантовую, зернистую природу света. В следующий раз, расставаясь с близким человеком в сумерках, обратите внимание на то, как вы видите удаляющуюся фигуру. Заметьте, что очертания удаляющегося объекта выглядят фрагментарными. Если бы световая энергия, отражающаяся от этого объекта и попадающая в оптические рецепторы вашей сетчатки, обладала волноподобной непрерывностью, то как минимум какой-то свет от каждой части объекта должен был бы всегда возбуждать ваши оптические рецепторы. Вы бы всегда видели полный образ. (Следует признать, что в слабом свете контраст между темным и светлым был бы не очень ясным, но это не влияло бы на четкость очертаний.) Однако вместо этого вы видите вовсе не четкие очертания, так как рецепторы ваших глаз реагируют на индивидуальные фотоны. В тусклом свете меньше фотонов, чем в ярком; поэтому в этой гипотетической сумеречной ситуации в любое данное время будут стимулироваться лишь немногие из ваших рецепторов — слишком немногие, чтобы определять очертания слабо освещенной фигуры. Следовательно, образ, который вы видите, будет фрагментарным.

Возможно, вам не дает покоя еще один вопрос: почему рецепторы не могут хранить данные бесконечно, пока мозг не соберет достаточно информации, чтобы собрать все фрагментарные картины в одно целое? К счастью для квантовых физиков, которые всегда отчаянно нуждаются в повседневных примерах квантовых явлений, оптические рецепторы могут хранить информацию лишь доли секунды. В тусклом свете в любой данный момент в ваших глазах будет возбуждаться недостаточно рецепторов для создания полного изображения. Когда в следующий раз в сумерках вы будете говорить «прощай» неясной удаляющейся фигуре любимого человека, не забудьте подумать о квантовой природе света; это, несомненно, уменьшит боль вашей разлуки.

Когда свет рассматривается как волна, он оказывается способным одновременно быть в двух (или более местах) — как в случае, когда он проходит через отверстия ткани зонтика, и образует дифракционную картину; однако, когда мы улавливаем его на фотографической пленке, он проявляется дискретно, отдельными пятнышками, подобно потоку частиц. Таким образом, свет должен быть и волной, и частицей. Парадоксально, не так ли? Дело касается одного из бастионов старой физики: однозначного описания на естественном языке. Кроме того, на карту поставлена сама идея объективности: зависит ли природа света — то, чем является свет, — от того, как мы его наблюдаем?

И как если бы парадоксы, касающиеся света, были недостаточно вызывающими, неизбежно возникает еще один вопрос: может ли материальный объект, например электрон, быть и волной, и частицей? Может ли он обладать двойственностью, подобной двойственности света? Физиком, который впервые поставил этот вопрос и упорно давал на него положительный ответ, потрясший всех его коллег, был французский аристократ Луи Виктор де Бройль.

Когда де Бройль примерно в 1924 г. писал свою кандидатскую диссертацию, он провел параллель между дискретностью стационарных орбит атома Бора и дискретностью звуковых волн, производимых гитарой. Параллель оказалась плодотворной.

Представьте себе движение звуковой волны в некоторой среде (рис. 4). Вертикальное смещение частиц среды меняется от ноля до максимума (гребень), обратно до ноля, до отрицательного максимума (впадины), опять до ноля, и так далее с увеличением расстояния. Максимальное вертикальное смещение в одном направлении (от ноля до гребня или впадины) называется амплитудой. Отдельные частицы среды движутся взад и вперед относительно своего покоящегося положения. Однако волна, проходящая через среду, распространяется. Волна представляет собой распространяющееся возмущение. Число гребней, проходящих через данную точку за секунду, называется частотой волны, а расстояние от гребня до гребня — длиной волны.

Рис. 4. Графическое представление волны

Щипок гитарной струны приводит ее в движение, но возникающие колебания называются стационарными (стоячими волнами), поскольку они не распространяются за пределы струны. В любом данном месте струны смещение частиц струны меняется во времени: имеет место волнистость, но волны не распространяются в пространстве (рис. 5). Распространяющиеся волны, которые мы слышим, приводятся в движение стоячими волнами колеблющихся струн.

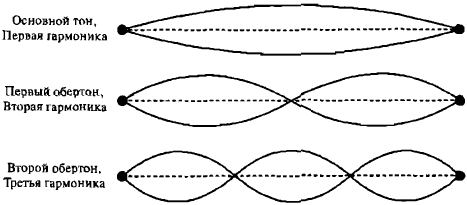
Рис. 5. Первые несколько гармоник стационарной, или стоячей, волны в гитарной струне

Музыкальная нота гитары состоит из целого ряда звуков — спектра частот. Де Бройля заинтересовало то, что стоячие волны гитарной струны создают дискретный спектр частот, называемых гармониками. Звук самой низкой частоты называется первой гармоникой, которая определяет слышимый нами тон. Более высокие гармоники — музыкальные звуки, придающие ноте ее характерное качество, — имеют частоты, кратные частоте первой гармоники.

Стационарность представляет собой свойство волн в ограниченном пространстве. Такие волны легко вызвать в чашке чая. Де Бройль спрашивал — являются ли электроны атома локализованными (удерживаемыми) волнами? Если да, то образуют ли они дискретные стационарные волновые паттерны? Например, может быть, самая низкая атомная орбита — это та, на которой один электрон образует стационарную волну наименьшей частоты — первую гармонику, — а более высокие орбиты соответствуют стационарным электронным волнам более высоких гармоник (рис. 6).

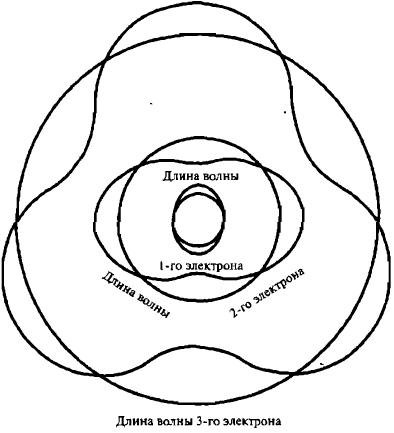
Рис. 6. Идея де Бройля: не могут ли электроны быть стационарными волнами в ограниченном пространстве атома?

Разумеется, де Бройль приводил в поддержку своей идеи гораздо более сложные доводы, но все равно ему было трудно добиться одобрения своей диссертации. В конце концов ее послали на отзыв Эйнштейну. Эйнштейну, который первым осознал двойственную природу света, было не трудно понять, что де Бройль вполне мог быть прав: материя вполне может быть такой же двойственной, как свет. Де Бройлю присудили искомую степень, когда Эйнштейн дал о его диссертации такой отзыв: «Это может выглядеть безумным, но, в действительности, это логично».

В науке окончательным арбитром всегда служит эксперимент. Правильность идеи де Бройля о волновой природе электрона блестяще продемонстрировал эксперимент, в котором пучок электронов пропускали через кристалл (трехмерный «зонтик», подходящий для дифракции электронов) и фотографировали. Получилась дифракционная картина (рис. 7).

Рис. 7. Концентрические дифракционные кольца показывают волновую природу электронов

Если материя — волна, язвительно заметил один физик другому в конце проходившего в 1926 г. семинара, посвященного волнам де Бройля, то должно быть волновое уравнение, описывающее волну материи. Физик, которому принадлежало это замечание, сразу же забыл о нем, но тот, кто его услышал, — Эрвин Шрёдингер — в дальнейшем открыл волновое уравнение для материи, теперь известное как уравнение Шредингера. Оно является краеугольным камнем, заменившим в новой физике законы Ньютона. Уравнение Шрёдингера используется для предсказания всех удивительных качеств субмикроскопических объектов, обнаруживаемых в наших лабораторных экспериментах. Вернер Гейзенберг открыл это же самое уравнение еще раньше, но в менее четкой математической форме. Математический формализм, выросший из работ Шрёдингера и Гейзенберга, называется квантовой механикой.

Предложенная де Бройлем и Шрёдингером идея волны материи порождает удивительную картину атома. Она объясняет простыми терминами три самых важных свойства атомов: их устойчивость, их тождественность друг другу и их способность восстанавливаться. Я уже объяснял, как возникает устойчивость, — это был великий вклад Бора. Тождественность атомов определенного вида — это просто следствие тождественности волновых паттернов в ограниченном пространстве; структура стационарных паттернов определяется тем, каким образом ограничивается движение электронов, а не их окружением. Музыка атома, его волновой паттерн, остается одной и той же, независимо от того, где он находится — на Земле или в туманности Андромеды. Более того, стационарный паттерн, зависящий только от условий своего ограничения, не имеет никаких следов прошлой истории, никакой памяти; он снова и снова восстанавливается в том же самом виде.

Волны электронов не похожи на обычные волны. Даже в эксперименте по дифракции индивидуальные электроны обнаруживаются на фотографической пластинке как локализованные индивидуальные события; только наблюдая паттерн, создаваемый всем пучком электронов, мы обнаруживаем свидетельство их волновой природы — дифракционную картину. Волны электронов — это волны вероятности, говорил физик Макс Борн. Они дают нам вероятности: например, мы, весьма вероятно, обнаружим частицу там, где волновые возмущения (или амплитуды) велики. Если вероятность нахождения частицы мала, амплитуда волны будет слабой. Представьте себе, что вы наблюдаете уличное движение с вертолета, висящего над улицами Лос-Анджелеса. Если бы автомобили описывались уравнением Шрёдингера, мы бы сказали, что волна сильна в местах транспортных пробок, а между пробками волна слаба.

Кроме того, волны электронов принято представлять как волновые пакеты. Используя понятие пакетов, мы можем делать амплитуду волны большей в определенных областях пространства, и малой во всех остальных местах (рис. 8). Это важно, поскольку волна должна представлять локализованную частицу. Волновой пакет — это пакет вероятности, и Борн утверждал, что для волн электронов квадрат амплитуды волны — технически называемый волновой функцией — в некоторой точке пространства дает нам вероятность обнаружения электрона в этой точке. Эта вероятность может быть представлена колоколообразной кривой (рис. 9).

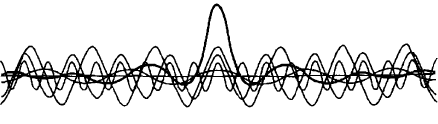
Рис. 8. Наложение многих простых волн образует типичный локальный волновой пакет (Из книги П. У. Аткинса «Кванты: справочник понятий», Оксфорд: Клейрдон Пресс, 1974)

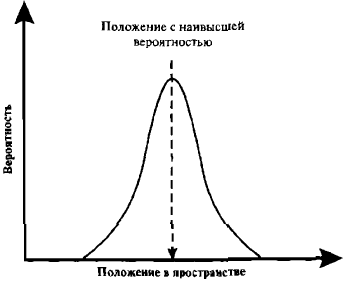
Рис. 9. Типичное распределение вероятности

Вероятность порождает неопределенность. Для электрона или любого другого квантового объекта мы можем говорить только о вероятности его нахождения в таком-то и таком-то месте, либо о том, что его импульс (произведение массы на скорость) равен тому-то и тому-то, но эти вероятности образуют распределение, описываемое колоколообразной кривой. Вероятность будет максимальной для некоторого значения положения, и это будет наиболее вероятное местонахождение электрона. Однако будет целая область положений, в которых есть значительные шансы обнаружить электрон. Ширина этой области соответствует неопределенности положения электрона. Такие же доводы позволяют нам говорить о неопределенности импульса электрона.

Исходя из подобных соображений, Гейзенберг математически доказал, что произведение неопределенностей положения и импульса электрона больше или равно определенному малому числу, называемому постоянной Планка. Это число, первоначально открытое Планком, устанавливает количественный масштаб, в котором квантовые эффекты становятся применимо большими. Если бы постоянная Планка не была такой малой, эффекты квантовой неопределенности вторгались бы даже в нашу повседневную макроскопическую реальность.

В классической физике любое движение определяется силами, которые им управляют. Коль скоро мы знаем начальные условия (положение и импульс объекта в некоторый начальный момент времени), мы можем вычислить его точную траекторию, используя уравнения движения Ньютона. Поэтому классическая физика ведет к философии детерминизма — идее возможности полного предсказания движения всех материальных объектов.

Принцип неопределенности подрывает философию детерминизма. Согласно принципу неопределенности, мы не можем одновременно точно определить положение и скорость (или импульс) электрона; любая попытка точного измерения одного делает неопределенным знание другого. Поэтому никогда нельзя точно определить начальные условия для вычисления траектории частицы, и понятие четко определенной траектории частицы становится непригодным.

По той же причине орбиты Бора не дают строгого описания местонахождения электрона: положение действительных орбит неопределенно. Мы действительно не можем говорить, что электрон, находящийся на том или ином энергетическом уровне, располагается на таком-то и таком-то удалении от ядра.

Рассмотрим несколько фантастических сценариев, авторы которых не осознавали значение принципа неопределенности или забывали о нем.

В научно-фантастической книге «Фантастическое путешествие» и снятом по ней фильме объектам придавали миниатюрные размеры путем уплотнения. Задумывались ли вы когда-либо о том, можно ли сжимать атомы? В конце концов, они, по большей части, состоят из пустого пространства. Возможно ли такое? Решите это сами, исходя из принципа неопределенности. Размер атома дает примерное представление о степени неопределенности положения его электронов. Уплотнение атома будет помещать его электроны в меньший объем пространства, тем самым снижая неопределенность их положения; но неопределенность их импульса должна возрастать. Увеличение неопределенности импульса электрона означает увеличение его скорости. Таким образом, в результате уплотнения скорость электронов возрастает и они более способны покидать атом.

В еще одном примере научной фантастики капитан Кирк (из классического телесериала «Звездный путь») дает команду: пуск! На приборной панели нажимают кнопку: оп-ля, люди, стоящие, на платформе исчезают, появляясь в месте назначения, которое, как предполагается, представляет собой неисследованную планету, но выглядит очень похоже на съемочный павильон в Голливуде. В одном из своих романов, основанном на сериале «Звездный путь», Джеймс Блиш попытался охарактеризовать этот процесс как квантовый скачок. Подобно тому как электрон перескакивает с одной атомной орбиты на другую, не пересекая промежуточное пространство, то же самое происходило бы и с командой космического корабля «Энтерпрайз». Вы можете видеть, в чем здесь проблема. То, когда и куда электрон совершит скачок, не подчиняется закону причинности и непредсказуемо вследствие законов вероятности и неопределенности квантового скачка. Подобный квантовый транспорт заставлял бы героев «Энтерпрайза», по крайней мере иногда, очень долго ждать, чтобы куда-то попасть.

Квантовые фантазии могут быть забавными, но конечная цель новой физики и этой книги серьезна. Она состоит в том, чтобы помочь нам иметь дело с нашей повседневной реальностью.

Предшествующая базовая информация помогает объяснить пару головоломных вопросов. Подразумевает ли квантовая картина электрона, движущегося волнами вокруг ядра, что заряд и масса электрона размазаны по всему атому? И означает ли тот факт, что свободный электрон распространяется так, как должна распространяться волна согласно теории Шрёдингера, что его заряд теперь размазан по всему пространству? Иными словами, как согласовать волновую картину электрона с тем фактом, что он обладает свойствами локализованной частицы? Ответы на эти вопросы весьма непросты.

Может казаться, что, по крайней мере, волновые пакеты дают возможность ограничивать электрон небольшим пространством. Увы, все не так просто. Волновой пакет, удовлетворяющий уравнению Шрёдингера в данный момент времени, с течением времени должен распространяться.

В некоторый начальный момент мы можем локализовать электрон в крохотной точке, но в течение секунд волновой пакет электрона будет распространяться по всему городу. Хотя первоначально вероятность нахождения электрона в крохотной точке подавляюще высока, всего через несколько секунд становится значимой вероятность появления электрона в любом месте в городе. А если мы будем ждать достаточно долго, электрон может появиться в любом месте во всей стране или даже во всей вселенной.

Именно это распространение волнового пакета способствует непрекращающимся шуткам о квантовой предопределенности среди знатоков. Например, возьмем такой квантово-механический способ материализации рождественской индюшки: приготовьте духовку и ждите — существует ненулевая вероятность того, что индюшка из соседнего магазина материализуется в вашей духовке.

К несчастью для любителя индюшатины, для таких массивных объектов, как индюшка, распространение происходит чрезвычайно медленно. Чтобы материализовать таким образом даже маленький кусочек индюшки, возможно, пришлось бы прождать все время существования вселенной.

А как насчет электрона? Как согласовать распространение волнового пакета электрона по всему городу с картиной локализованной частицы? Ответ в том, что мы должны учитывать в своих вычислениях акт наблюдения.

Если мы хотим измерить заряд электрона, мы должны уловить его с помощью чего-то вроде облака пара в конденсационной камере. В результате этого измерения мы должны допускать, что волна электрона схлопывается, так что теперь мы способны видеть путь электрона через облако пара (рис. 10). Согласно Гейзенбергу, «путь электрона начинает существовать только когда мы его наблюдаем». Производя измерение, мы всегда обнаруживаем электрон, локализованный в качестве частицы. Можно говорить, что наше измерение редуцирует волну электрона к состоянию частицы.

Рис. 10. Трек электрона в облаке пара

Когда Шрёдингер предлагал свое волновое уравнение, он и другие думали, что им, возможно, удалось освободить физику от квантовых скачков — от прерывистости, — поскольку волновое движение непрерывно. Однако корпускулярную природу квантовых объектов было необходимо согласовать с их волновой природой. Поэтому были предложены волновые пакеты. Наконец, с признанием распространения волнового пакета и осознанием того, что именно измерение должно вызывать мгновенное схлопывание размеров пакета, мы видим, что схлопывание должно быть прерывистым (непрерывное схлопывание требовало бы времени).

Кажется, будто не может быть квантовой механики без квантовых скачков. Однажды Шрёдингер посетил Бора в Копенгагене, где он целыми днями протестовал против квантовых скачков. Говорят, что в конце концов он сдался, раздраженно воскликнув: «Если бы я знал, что нужно признавать этот проклятый квантовый скачок, то никогда бы не связался с квантовой механикой».

Вернемся обратно к атому: если мы измеряем положение электрона, находящегося в атомном стационарном состоянии, то снова схлопываем его облако вероятности, находя его в определенном положении, а не размазанным повсюду. Делая большое число измерений в поисках электрона, мы будем чаще находить его в тех местах, где вероятность его нахождения высока, в соответствии с предсказанием уравнения Шрёдингера. Действительно, если после большого числа измерений мы графически изобразим измеренные положения, это будет выглядеть в точности подобно размытому распределению орбиты, которое дает решение уравнения Шрёдингера (рис. 11).

Рис. 11. Результаты многократных измерений положения электрона в атоме водорода на самой низшей орбите. Очевидно, что волна электрона обычно схлопывается там, где предсказываемая вероятность его нахождения высока, что дает размытую орбиту

Как с этой точки зрения выглядит летящий электрон? Когда мы делаем начальное наблюдение любого распространяющегося субмикроскопического объекта, то обнаруживаем его локализованным в качестве частицы в крохотном волновом пакете. Однако после наблюдения пакет рассеивается, и рассеяние пакета представляет собой облако нашей неопределенности в отношении пакета. Если мы наблюдаем опять, то пакет снова локализуется, но между нашими наблюдениями он всегда рассеивается.

По словам физика-философа Генри Маргенау, наблюдение электронов подобно наблюдению светлячков летним вечером. Вы можете видеть вспышку здесь, и еще мелькание света там, но не имеете никакого представления о том, где находится светлячок между вашими наблюдениями. Вы не можете сколько-либо уверенно определить его траекторию. Даже для такого макроскопического объекта, как луна, квантовая механика предсказывает, в сущности, ту же картину — единственная разница в том, что рассеяние волнового пакета неизмеримо мало (но между наблюдениями отлично от нуля).

Теперь мы подходим к сути вопроса. Всякий раз, когда мы измеряем квантовый объект, он проявляется в каком-то одном месте как частица. Распределение вероятности просто идентифицирует то место (или те места), где его вероятно обнаружить, когда мы его измеряем — не более того. Когда мы его не измеряем, квантовый объект рассеивается, и существует в одно и то же время более чем в одном месте, точно так же, как волна или облако — никак не меньше.

Квантовая физика предлагает новое и волнующее мировоззрение, которое ставит под сомнение такие старые концепции, как детерминистские траектории и причинная непрерывность. Если начальные условия не определяют навсегда движение объекта, если каждый момент, когда мы наблюдаем, становится новым началом, значит на фундаментальном уровне мир является творческим.

Жил был казак, который видел, как почти каждый день, примерно в одно и то же время, раввин переходил городскую площадь. Однажды он из любопытства спросил: «Куда вы идете, рэбби?»

Раввин отвечал: «Я точно не знаю».

«Вы проходите этой дорогой каждый день в это время. Конечно, вы знаете, куда идете».

Когда раввин стал настаивать, что он этого не знает, казак рассердился, потом стал подозрительным и в конце концов отвел раввина в тюрьму. Как раз, когда он запирал дверь камеры, раввин посмотрел на него и мягко сказал: «Видите, я не знал».

До того как казак его остановил, раввин знал, куда он идет, но после этого уже не знал. Остановка (мы можем назвать ее измерением) открывала новые возможности. Таков смысл квантовой механики. Мир не определяется раз и навсегда начальными условиями. Каждое событие измерения является потенциально творческим и может открывать новые возможности.

Новый способ понимания парадокса двойственности волны-частицы предложил Бор. По его словам, волновая и корпускулярная природы электрона представляют собой не двойственные, а просто полярно противоположные качества. Это взаимодополняющие качества, открывающиеся нам во взаимодополняющих экспериментах. Когда мы берем дифракционную картину электрона, то открываем его волновую природу; когда мы прослеживаем его в облаке пара, то видим его корпускулярную природу. Электроны не являются ни волнами, ни частицами. Их можно называть «волночастицами», ибо их подлинная природа превосходит оба описания. В этом состоит принцип дополнительности.

Поскольку обдумывание того факта, что один и тот же квантовый объект обладает такими, казалось бы, противоречивыми свойствами, как волновые и корпускулярные, может быть опасно для человеческой психики, природа предусмотрела амортизатор. Принцип дополнительности Бора уверяет нас, что хотя квантовые объекты обладают и волновыми, и корпускулярными свойствами, мы можем в рамках любой экспериментальной обстановки в любое данное время измерять только один аспект волночастицы. Мы выбираем, какой аспект волночастицы мы хотим увидеть, выбирая соответствующую экспериментальную обстановку.

Поняв революционные идеи новой физики, было бы совершенно неверно думать, что физика Ньютона была полностью неправильной. Старая физика продолжает жить в сфере большей части (но не всей) грубой материи в качестве частного случая новой физики. Важная особенность науки состоит в том, что когда новый порядок сменяет старый, он, обычно, расширяет область своего применения. В старой области математические уравнения старой физики остаются справедливыми (подтверждаясь экспериментальными данными). Поэтому в сфере классической физики выводы квантовой физики о движении объектов четко соответствуют тем, что делаются с помощью ньютоновской математики при допущении, что тела, с которыми мы имеем дело, являются классическими. Этот принцип соответствия сформулировал Бор. Взаимоотношение между классической и квантовой физикой в каком-то смысле похоже на зрительную иллюзию. «Моя жена и моя теща» (рис. 12). Что вы видите на этом рисунке? Сначала вы видите или жену, или тещу. Я всегда вижу сначала жену. В действительности, вам может потребоваться некоторое время, чтобы обнаружить на рисунке второй образ. Если вы присматриваетесь к нему, внезапно возникает второй образ. Подбородок жены превращается в нос тещи, ее шея — в подбородок более старой женщины, и так далее. Возможно, вы поражаетесь — что происходит? Линии рисунка остаются теми же, но внезапно для вас становится возможным новый способ восприятия картины. Очень скоро вы обнаруживаете, что можете легко переходить от старой картинки к новой и обратно. В любой момент вы по-прежнему видите только один из двух образов, но ваше сознание расширилось так, что вы осознаете их двойственность. В таком расширенном состоянии осознания начинает становиться понятной странность квантовой физики. Она даже становится волнующей. Перефразируя слова Гамлета, обращенные к Горацио, можно сказать — в небесах и на земле есть много вещей, которые и не снились классической физике.

Рис. 12. Моя жена и моя теща

Квантовая механика дает нам более широкую перспективу, новый контекст, расширяющий наше восприятие в новую область. Мы можем видеть природу как отдельные формы — волны, либо частицы — или можем обнаруживать дополнительность: идею, что одной и той же вещи присущи и волновые, и корпускулярные свойства.

Согласно так называемой Копенгагенской интерпретации квантовой механики, разработанной Бором, Гейзенбергом и Борном, мы рассчитываем квантовые объекты как волны и интерпретируем волны вероятностным образом. Мы определяем их атрибуты — такие, как положение и импульс — отчасти неопределенно и понимаем их с учетом принципа дополнительности. Вдобавок фундаментальными аспектами поведения квантового объекта считаются отсутствие непрерывности и квантовые скачки — например, схлопывание расползающегося волнового пакета при наблюдении. Еще один аспект квантовой механики — неразделимость. Разговор о квантовом объекте без разговора о том, как мы его наблюдаем, не имеет смысла, поскольку одно неотделимо от другого. Наконец, для массивных макрообъектов предсказания квантовой механики совпадают с предсказаниями классической физики. Это вводит запрет на проявление таких квантовых эффектов, как вероятность и прерывистость в макроскопической сфере природы, которую мы наблюдаем непосредственно с помощью органов чувств. Классическое соответствие маскирует квантовую реальность.

Принципы квантовой теории позволяют отказаться от необоснованных допущений материального реализма.

Допущение 1: Строгая объективность. Основное допущение материализма состоит в том, что существует независимая от нас материальная вселенная. Это допущение обладает некоторой очевидной операционной обоснованностью и зачастую считается необходимым для осмысленного занятия наукой. Действительно ли это допущение обоснованно? Квантовая физика показывает, что мы выбираем, какой аспект — волновой или корпускулярный — будет демонстрировать квантовый объект в той или иной ситуации. Более того, наше наблюдение схлопывает квантовый волновой пакет в локализованную частицу. Субъекты и объекты неразделимо связаны воедино. Если это так, то как можно придерживаться допущения строгой объективности?

Допущение 2: Причинный детерминизм. Еще одно допущение классической науки, подкрепляющее материальный реализм, — это то, что мир является фундаментально детерминистическим: нам нужно знать только силы, действующие на каждый объект, и начальные условия (начальные скорость и положение объекта). Однако принцип квантовой неопределенности говорит, что мы никогда не можем одновременно определять и скорость, и положение объекта с абсолютной точностью. В нашем знании начальных условий всегда будет содержаться ошибка, и строгий детерминизм неприемлем. В равной мере подозрительна и сама идея причинности. Поскольку поведение квантовых объектов носит вероятностный характер, строгое причинно-следственное описание поведения единичного объекта невозможно. Вместо этого, говоря о больших группах частиц, мы имеем статистическую причину и статистическое следствие.

Допущение 3: Локальность. Допущение локальности — того, что все взаимодействия между материальными объектами опосредуются локальными сигналами, — имеет решающее значение для материалистического воззрения, согласно которому объекты существуют, по существу, отдельно и независимо друг от друга. Однако если волны распространяются на огромные расстояния, а затем внезапно схлопываются, когда мы производим измерения, то влияние нашего измерения не передается локально. Таким образом, локальность исключается. Это еще один смертельный удар по материальному реализму.

Допущения 4 и 5. Материализм и эпифеноменализм. Материализм утверждает, что субъективные ментальные феномены представляют собой всего лишь эпифеномены материи и могут быть полностью сведены к материальному мозгу. Однако согласно принципу дополнительности и идее смешения субъекта и объекта для понимания поведения квантовых объектов нам, по-видимому, необходимо учитывать сознание — нашу способность делать выбор. Более того, кажется абсурдным, что эпифеномен материи может воздействовать на материю: если сознание — это эпифеномен, то как оно может «схлопывать» рассредоточенную волну квантового объекта в локализованную частицу при проведении квантового измерения?

Несмотря на принцип соответствия, новая парадигма физики — квантовая физика — противоречит данным материального реализма. Не существует способа обойти стороной этот вывод. Мы не можем говорить, ссылаясь на принцип соответствия, что классическая физика справедлива для макрообъектов для всех практических целей, и что коль скоро мы живем в макромире, то будем допускать, что квантовая странность ограничена субмикроскопической сферой природы. Напротив, странность преследует нас и на макроуровне. Если мы делим мир на сферы классической и квантовой физики, возникают неразрешимые квантовые парадоксы.

В Индии люди придумали хитроумный способ ловить мартышек с помощью сосуда с орехами. Мартышка засовывает руку в сосуд, захватывая пригоршню орехов. Увы, зажав пищу в кулаке, она уже не может вытащить руку — горлышко сосуда слишком узкое. Ловушка действует потому, что жадность мартышки не дает ей выпустить орехи. Аксиомы материального реализма — материализм, детерминизм, локальность и т.д. — хорошо служили нам в прошлом, когда наши знания были более ограниченными, чем сегодня, но теперь они стали для нас ловушкой. Возможно, нам придется отказаться от орехов определенности, чтобы воспользоваться свободой, лежащей за пределами материальной арены.

Если материальный реализм не может быть адекватной философией для физики, то какая философия способна иметь дело со всеми странностями квантового поведения? Это философия монистического идеализма, которая лежит в основе всех религий мира.

Традиционно, только религии и гуманитарные дисциплины признают ценность человеческой жизни за пределами физического выживания — ценность, обусловленную нашей любовью к прекрасному; нашими творческими способностями в искусстве, музыке и мысли; и нашей духовностью в интуиции единства. Естественные науки, запертые в рамках классической физики и ее философского багажа материального реализма, были соблазнителем скептицизма. Теперь новая физика остро нуждается в новой, освобождающей философии, подходящей для современного уровня наших знаний. Если монистический идеализм подходит для этого, то естественные и гуманитарные науки, наряду с религиями, впервые со времен Декарта, смогут идти рука об руку в поиске всей человеческой истины.