Среди множества стратегий решения математических задач есть такая, которая позволяет выйти из положения, когда вы «упираетесь в стену». Это подход к задаче с другой точки зрения. Ниже приведен пример такой стратегии, который является классическим в силу простоты и кардинальности изменения метода решения. В этом примере обычный подход дает правильный ответ, однако он громоздок и нередко приводит к арифметическим ошибкам. Рассмотрим следующую задачу.

В школе 25 классов, каждый из которых выставляет бас­кетбольную команду для участия в общешкольном турнире. По условиям турнира команда, проигравшая в одной встрече, выбывает из соревнования. В школе всего один спортивный зал, и директор хочет знать, сколько встреч придется провести в нем, чтобы определить победителя.

Типичное решение этой задачи заключается в моделировании реального турнира, в котором 12 случайно выбранных команд встречаются с другой группой из 12 команд, а одна команда освобождается от соревнований. Победители затем встречаются друг с другом, как показано ниже.

Любые 12 команд играют против других 12 команд, в результате чего определяются 12 победителей.

Во втором круге 6 победителей встречаются с 6 другими победителями, в результате чего определяются 6 победителей.

В третьем круге 3 победителя встречаются с 3 другими победителями, в результате чего определяются 3 победителя.

3 победителя + 1 команда (освобожденная от соревнований) = 4 команды.

В четвертом круге 2 оставшиеся команды встречаются с 2 оставшимися командами, в результате чего определяются 2 победителя турнира.

В пятом круге 1 команда играет против 1 команды за звание чемпиона.

Теперь подсчитаем количество проведенных игр.

Суммарное количество проведенных игр равно:

12 + 6 + 3 + 2 + 1 =24.

Такой метод решения кажется вполне разумным и определенно правильным.

Если подойти к этой задаче с другой точки зрения и определять проигравших, а не победителей, то решение будет значительно проще. В этом случае мы задаемся вопросом, сколько должно быть проигравших, чтобы определить одного чемпиона? Понятно, что проигравших должно быть 24. Чтобы появились 24 проигравших, нужно провести 24 игры. Ответ найден. Взгляд на задачу с другой точки зрения — интересный подход, который может оказаться полезным в различных ситуациях.

Для получения еще одной альтернативной точки зрения на задачу представьте, что в составе наших 25 команд одна является профессио­нальной баскетбольной командой, которая гарантированно побеждает в турнире. Каждая из оставшихся 24 команд при встрече с профессио­нальной командой неизбежно проигрывает. И опять мы видим, что для определения чемпиона нужно провести 24 игры. Это должно показать вам действенность данного метода решения задач. Посмотрим теперь, какие задачи можно эффективно решать с помощью принятия другой точки зрения.

Задача 4.1

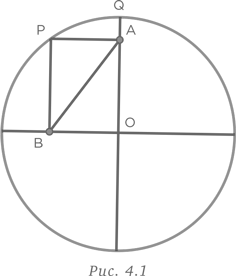
На контуре круга O выбрана точка P (рис. 4.1). Из этой точки к взаимно перпендикулярным диаметрам проведены перпендикуляры PA и PB. Если AB = 12, то чему равна площадь круга, выраженная через π?

Обычный подход

Большинство пытается решить задачу с помощью теоремы Пифагора, поскольку треугольники PAB и OAB являются прямоугольными. Такой подход, однако, заводит в тупик из-за того, что для применения теоремы Пифагора недостаточно информации.

Образцовое решение

Эту задачу можно решить несколькими способами. Один из них — рассмотрение экстремумов. Предположим, что точка P на контуре круга совпадает с точкой Q. В этом случае отрезок AB должен совпадать с отрезком QO, который представляет собой радиус круга. Таким образом, площадь круга равна 144π.

Задачу также можно решить, посмотрев на нее с другой точки зрения. Четырехугольник с тремя прямыми углами является прямоугольником. Отрезок AB — диагональ прямоугольника. PO также диагональ прямоугольника. Поскольку диагонали прямоугольника равны, радиус круга PO = 12, а площадь круга равна 144π.

Задача 4.2

Стандартную колоду из 52 игральных карт делят случайным образом на две стопки по 26 карт в каждой. Как количество красных карт в одной стопке соотносится с количеством черных карт в другой?

Обычный подход

При решении этой задачи, как правило, количество черных и красных карт в каждой стопке представляют следующим образом:

B1 = количество черных карт в стопке 1;

B2 = количество черных карт в стопке 2;

R1 = количество красных карт в стопке 1;

R2 = количество красных карт в стопке 2.

Поскольку общее количество черных карт равно 26, можно записать, что B1 + B2 = 26, а поскольку общее количество карт в стопке 2 равно 26, мы получаем R2 + B2 = 26.

Вычитание второго уравнения из первого, дает: B1 – R2 = 0. Таким образом, B1 = R2, т.е. количество красных карт в одной стопке равно количеству черных карт в другой. Хотя такое решение дает ответ, назвать его изящным нельзя. Наша цель в этой главе — найти такое решение, которое демонстрирует красоту и силу математики.

Образцовое решение

В качестве альтернативы возьмем все красные карты из стопки 1 и обменяем их на черные карты из стопки 2. Теперь все черные карты находятся в одной стопке, а красные — в другой. Таким образом, количество красных карт в одной стопке и количество черных карт в другой стопке должны быть равными. Задачу позволяет решить простая логика — нужно лишь взглянуть на эту задачу с другой точки зрения.

Задача 4.3

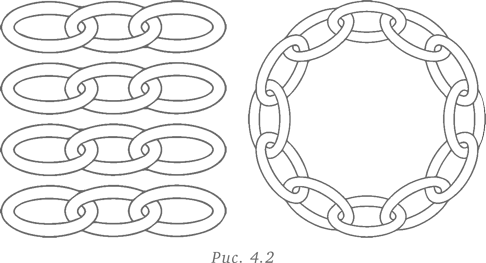
Лоэнгрину дали четыре отрезка цепи (рис. 4.2), в каждом из которых три звена. Покажите, как соединить эти четыре отрезка в замкнутую цепь, разомкнув и сомкнув не более трех звеньев.

Обычный подход

Обычно сначала пытаются разомкнуть последнее звено одного отрезка, присоединить его к другому отрезку и получить цепь из 6 звеньев. Затем размыкают звено третьего отрезка и присоединяют его к 6-звенной цепи, получая 9-звенную цепь. Присоединив последний отрезок к 9-звенной цепи, получают 12-звенную цепь, которая, однако, не является замкнутой. Таким образом, традиционный подход обычно завершается неудачей. Некоторые пробуют другие комбинации размыкания/замыкания звеньев каждого отрезка цепи, однако такой подход не приносит желаемого результата.

Образцовое решение

Эта задача хорошо решается с помощью стратегии принятия другой точки зрения. Можно даже сказать, что такой подход просто неоценим в данном случае. Вместо того, чтобы пытаться разомкнуть и замкнуть одно звено на каждом отрезке цепи, другая точка зрения предполагает размыкание всех звеньев одного отрезка цепи и использование этих звеньев для соединения трех оставшихся отрезков цепи и получения требуемой замкнутой цепи. Это быстро приводит к правильному решению.

Задача 4.4

Какие натуральные числа менее 100 дают остаток 3 при делении на 7 и остаток 4 при делении на 5?

Обычный подход

Рассмотрим ряд натуральных чисел менее 100, которые дают остаток 3 при делении на 7: {3, 10, 17, 24, 31, 38, 45, 52, 59, 66, 73, 80, 87, 49}. Теперь рассмотрим ряд натуральных чисел менее 100, которые дают остаток 4 при делении на 5: {4, 9, 14, 19, 24, 29, 34, 39, 44, 49, 54, 59, 64, 69, 74, 79, 84, 89, 94, 99}.

Сравнив эти два ряда, находим три совпадающих числа: 24, 59 и 94.

Образцовое решение

Попробуем взглянуть на эту задачу с другой точки зрения. Искомые числа должны иметь форму 7n + 3, а также форму 5k + 4, где n и k — целочисленные неизвестные. Объединим эти величины так, чтобы искать числа в форме 35r + p, где r и p — целочисленные неизвестные. Первый ряд чисел, имеющих форму 7n + 3, также можно представить, как 35r + 3, 35r + 10, 35r + 17, 35r + 24 и 35r + 31. Только одно из этих чисел имеет также форму 5k + 4, а именно 35r + 24. Для того, чтобы узнать, какие числа менее 100, удовлетворяют этому соотношению, зададим r = 0, 1 и 2 и получим три искомых числа: 24, 59 и 94.

Задача 4.5

Какое из следующих двух выражений больше, √5 + √8 или √4 + √10

Обычный подход

Учитывая нынешнее распространение калькуляторов, не удивительно, что люди обычно извлекают квадратный корень из каждого числа, затем определяют их суммы и получают требуемый ответ. Хотя такой подход довольно эффективен, его, конечно, не назовешь изящным.

Образцовое решение

Взглянем на задачу с другой точки зрения, а именно возведем в квадрат каждую из этих сумм и посмотрим, каким будет результат.

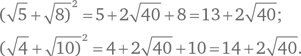
Упростив, таким образом, условия, мы видим, что сумма является большей из двух величин.

Задача 4.6

Чему равны все положительные целочисленные значения переменной n, для которой дробь 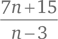также является целым числом?

Обычный подход

Первой реакцией на эту задачу является попытка подставить разные значения n и посмотреть, какой результат будет целым числом. Например, если принять n = 4, мы получим 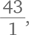т.е. целое число. Хотя такой подход и позволяет выявить некоторые значения n, очень трудно сказать, все ли значения найдены. В результате обычно получается неполный ответ.

Образцовое решение

Воспользуемся стратегией принятия другой точки зрения. Для начала выполним деление:

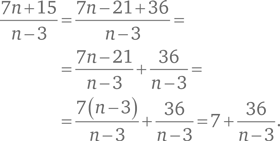
Чтобы эта величина была целым числом, n – 3 должно быть пропорцио­нально 36. Делителями для числа 36 являются 1, 2, 3, 4, 6, 9, 12, 18 и 36. Таким образом:

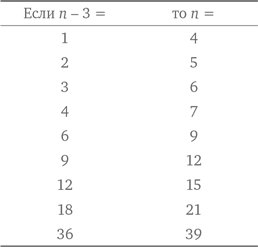
Значения n, при которых 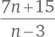является целым числом, равны 4, 5, 6, 7, 9, 12, 15, 21 и 39.

Задача 4.7

Каждый из 10 придворных ювелиров дает королевскому советнику г-ну Саксу стопку золотых монет. В каждой стопке находится 10 монет. Полноценные монеты весят 1 унцию. Однако в одной из стопок находятся «неполновесные» монеты, каждая из которых весит на 0,1 унции меньше. Г-н Сакс хочет выявить ювелира-жулика и стопку неполновесных монет с помощью всего лишь одного взвешивания. Как это сделать?

Обычный подход

Традиционная процедура начинается со случайного выбора стопки и ее взвешивания. Такой метод проб и ошибок дает искомый результат всего в 1 случае из 10. Учитывая это, можно попытаться решить задачу путем логического рассуждения. Прежде всего, если все монеты полновесные, их общий вес должен составлять 10 × 10 = 100 унций. Каждая из 10 неполновесных монет имеет меньший вес, поэтому недостача должна составить 10 × 0,1 = 1 унцию. Однако подход с точки зрения общей недостачи ничего не дает, поскольку она может оказаться в любой из стопок — в первой, второй, третьей и т.д.

Образцовое решение

Попробуем решить задачу, организовав данные иначе. Нам необходимо найти такой метод обнаружения недостачи, позволяющий идентифицировать стопку, из которой взяты неполновесные монеты. Присвоим стопкам номера № 1, № 2, № 3, № 4, …, № 9, № 10. Затем возьмем одну монету из стопки № 1, две монеты из стопки № 2, три монеты из стопки № 3, четыре монеты из стопки № 4 и т.д. Всего у нас получилось 1 + 2 + 3 + 4 + … + 8 + 9 + 10 = 55 монет. Если все монеты полновесные, то их общий вес должен составить 55 унций. Если обнаружится недостача 0,5 унции, значит в навеске присутствуют 5 неполновесных монет из стопки № 5. Если обнаружится недостача 0,7 унции, значит в навеске присутствуют 7 неполновесных монет из стопки № 7 и т.д. Таким образом, г-н Сакс может легко определить стопку неполновесных монет и ювелира, который принес эти монеты.

Задача 4.8

Ресторан быстрого питания продает куриные наггетсы в коробках по 7 штук и по 3 штуки. Какое наибольшее количество наггетсов нельзя купить?

Обычный подход

Мы просто пытаемся найти ответ путем перебора сочетаний 7 и 3 до тех пор, пока не дойдем до точки, начиная с которой можно купить любое количество наггетсов.

По всей видимости, наибольшее количество наггетсов, которое нельзя купить, равно 11. После этого все, что нужно, это добавлять 3 или 7.

Образцовое решение

Здесь мы обратимся к идее, привносящей в решение определенное изящество, и предоставим читателю возможность самому разобраться, почему это так, а не иначе. Существует теорема, известная под названием «теорема макнаггетсов». В соответствии с ней, если McDonald's продает макнаггетсы в коробках по a или b штук, где a и b не имеют общих множителей, то наибольшее количество макнаггетсов, которое нельзя купить, равно ab – (a + b). Например, если они продаются в коробках по 8 и 5 штук, то наибольшее количество макнаггетсов, которое нельзя купить, составляет 8 × 5 – (8 + 5) = 40–13 = 27.

В нашей задаче, наибольшее количество наггетсов, которое нельзя купить, равно 3 × 7 – (3 + 7), или 21 – 10 = 11.

Задача 4.9

Упростите каждое из следующих выражений:

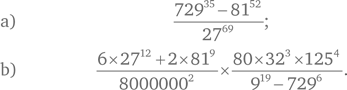
Обычный подход

Хотя есть соблазн взять калькулятор и вычислить значение этих выражений, нередко наши надежды не оправдываются, и мы получаем на табло лишь сообщение error.

Образцовое решение

Подойдем к решению этой задачи с другой точки зрения. Учитывая, что число 3 возводить в степень довольно просто, решим задачу следующим образом:

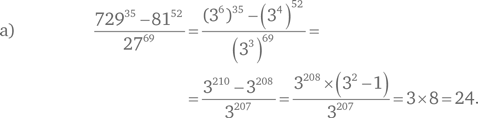
Второе выражение можно упростить, разбив числа на простые множители следующим образом:

Задача 4.10

И у Вольфганга, и у Людвига есть целое число евро, причем каждое из них меньше 100. Когда они посчитали свои деньги, оказалось, что три четверти суммы Вольфганга равны двум третям суммы Людвига. Какое максимальное число евро может быть у каждого из них?

Обычный подход

Первая реакция — применить алгебраический подход. Мы можем составить одно уравнение с двумя неизвестными. Пусть W представляет количество евро у Вольфганга, а L — количество евро у Людвига. Наше уравнение имеет следующий вид:

Умножим обе части уравнения на 12 и получим: 9W = 8L. Решение уравнения для W дает следующий результат:

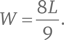
Поскольку у каждого из мальчиков по целому числу евро, сумма Людвига должна быть кратной 9, т.е. 9, 18, 27, 36, …, 99. Теперь можно подставить каждое из этих чисел в уравнение и определить количество евро у Людвига. Наибольшее количество евро, которое может иметь Людвиг, составляет 11 × 9, или 99 евро (менее, чем 100). Мы знаем, что суммы Людвига (66 евро) равны суммы Вольфганга. Таким образом, сумма Вольфганга составляет 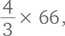или 88 евро, а сумма Людвига — 99 евро.

Образцовое решение

Воспользуемся арифметическим подходом и взглянем на задачу с другой точки зрения. Поскольку суммы Вольфганга равны суммы Людвига, найдем эквивалентные дроби с одинаковым числителем:

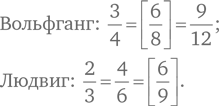
Если у Вольфганга 8 евро, а у Людвига 9 евро, то части их сумм становятся одинаковыми и равными 6 евро. Поэтому ответ должен быть равен произведению одного и того же множителя на 8 и 9. Таким образом, наибольшая сумма, которую может иметь Людвиг, составляет 11 × 9, или 99 евро, а наибольшая сумма Вольфганга — 11 × 8, или 88 евро.

Ответ можно проверить, определив величину от 88 евро (66) и от 99 евро (66).

Задача 4.11

На рис. 4.3 ширина прямоугольника AEFK равна AK = 8, а длина AE разделена на четыре части AB = 1, BC = 6, CD = 4 и DE = 2. Чему равна площадь четырех закрашенных треугольников?

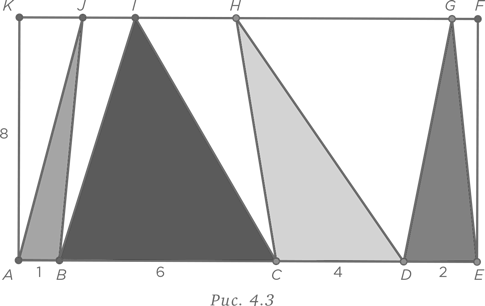
Обычный подход

Очевидный подход — найти площадь каждого из четырех треугольников и сложить их. Во всех четырех случаях высота треугольника равна ширине прямоугольника AK = 8. Таким образом, площади четырех треугольников составляет:

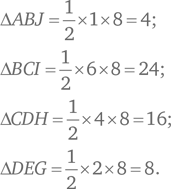
Сумма этих площадей равна 4 + 24 + 16 + 8 = 52.

Образцовое решение

Воспользуемся нашей стратегией принятия другой точки зрения на решение задачи. Треугольники имеют одну и ту же высоту, а именно 8. Сумма оснований четырех треугольников равна длине прямоугольника, т.е. 13. Таким образом, площадь четырех закрашенных треугольников равна половине площади прямоугольника, или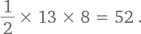

Задача 4.12

Определите, сколько чисел можно составить из цифр от 1 до 9 при условии, что цифры в этих числах должны располагаться в порядке возрастания.

Обычный подход

Большинство людей, скорее всего, воспользуются методом проб и ошибок и попытаются выяснить, нет ли здесь какой закономерности, и будут добавлять в список одно число за другим, т.е. сначала однозначные числа, затем двухзначные, трехзначные и т.д. Если выполнить эту работу тщательно, то можно получить правильный ответ, однако такой подход трудоемок.

Образцовое решение

Рассмотрим сначала набор целых чисел, имеющихся в нашем распоряжении {1, 2, 3, 4, 5, 6, 7, 8, 9}. Каждое под­множество этих цифр, за исключением пустого, должно давать одно из искомых чисел. Например, подмножество {3, 5, 7, 9} дает число 3579. Вопрос в том, сколько таких подмножеств можно выделить в нашем ряду из девяти цифр. Их количество равно 29 = 512. Вместе с тем сюда вошло пустое подмножество, которое необходимо вычесть. Таким образом, мы получаем 29 – 1 = 511 подмножеств из 9 цифр, каж­дое из которых дает число, где в соответствии с условием задачи, цифры могут располагаться в порядке возрастания.

Задача 4.13

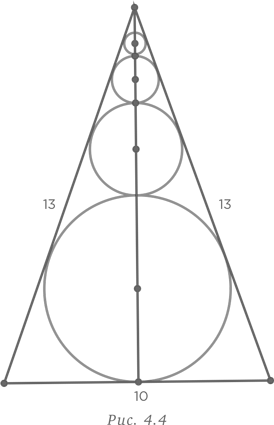
На рис. 4.4 показан равнобедренный треугольник с бесконечным рядом окружностей, каждая из которых касается двух равных сторон треугольника и соседних окружностей, а нижняя окружность касается основания треугольника. Стороны равнобедренного треугольника равны 13, 13 и 10. Чему равна сумма длин этих окружностей?

Обычный подход

Занудный по определению подход предполагает вычисление длины каждой окружности с последующим определением суммы их длин. Подсчеты в этом случае очень трудо­емки, но при тщательном выполнении они могут дать правильный ответ.

Образцовое решение

Воспользуемся стратегией рассмотрения задачи с другой точки зрения. С помощью теоремы Пифагора находим, что высота равнобедренного треугольника равна 12. Заметим, что сумма диаметров бесконечного числа окружностей равна высоте равнобедренного треугольника. Таким образом, сумма длин окружностей равна сумме диаметров, умноженной на π, т.е. 12π.

Задача 4.14

Чему равен наименьший неотрицательный остаток при делении 227 на 123?

Обычный подход

Как правило, при решении этой задачи люди тратят кучу времени на определение значения числа 227, а потом делят результат на 123.

Образцовое решение

Мы подойдем к решению задачи с другой точки зрения. Вместо развертывания 227 в число без степени разложим его на числа в степени:

227 = (27) (117) = (27) (112) (112) (112) (11) = (123 + 5) (123 – 2) (123 – 2) (123 – 2) (11).

Теперь вспомним, что произведение двух двучленов вида 123 + s и 123 + t можно представить как 123k + st:

(123 + s) (123 + t) = 1232 + 123s + 123t + st = 123 (123 + s + t) + st = 123k + st.

Таким образом, мы получаем:

123n – 440 = 123n – 492 + 52 = 123 (n – 4) + 52.

При делении числа 227 на 123 остаток равен 52.

Задача 4.15

Во время футбольного матча команды получают 2 очка за сейфти, 3 очка за гол в ворота и 7 очков за тачдаун. Если отбросить 2 очка за сейфти, то команды смогут получать лишь по 3 и по 7 очков. Каково максимальное значение счета, которое нельзя получить в этом матче?

Обычный подход

Очевидный подход — выписывать все возможные значения счета до тех пор, пока не обнаружится максимальное значение, которое невозможно получить. Такой метод, однако, не дает уверенности в том, что не существует более высокое значение.

Образцовое решение

В этом случае можно воспользоваться стратегией принятия другой точки зрения. Вместо поисков значений счета, которые нельзя получить, определим значения, которые можно получить. Счет, который можно набрать, зарабатывая очки на голах в ворота, составляет 3, 6, 9, 12, 15, … Счет, который можно заработать на очках за тачдаун, составляет 7, 14, 21, 28, … Другие значения получаются в результате прибавления очков за гол в ворота или за тачдаун к предыдущему счету. Таким образом, значения, которые нельзя получить, составляют 2, 4, 5, 8, 11. Любой счет, начиная с 12, является доступным, как видно из следующего:

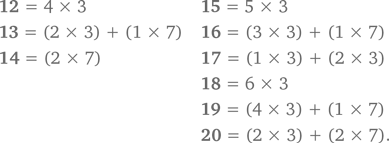
Таким образом, наивысший счет, который нельзя получить, равен 11.

Интересно отметить, что эта ситуация описывается чисто математически.

Наивысший счет, который нельзя получить при использовании двух простых чисел (a и b), равен произведению этих чисел за вычетом их суммы. В нашем случае это (7 × 3) – (7 + 3) = 11.

Задача 4.16

Число 6! (читается как «шесть факториал») равно произведению 6 × 5 × 4 × 3 × 2 × 1 = 720. Найдите значение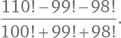

Обычный подход

Обычно так и подмывает выписать все факториалы, взять калькулятор или компьютер и вычислить фактические результаты. Это, конечно, позволит получить ответ, но потребует массы арифметических расчетов.

Образцовое решение

Давайте применим стратегию принятия другой точки зрения. Каждый из факториалов можно представить как число, кратное 98! Например, 100! можно записать как 100 × 99 × 98!, а 99! — как 99 × 98! В результате мы получаем:

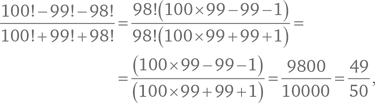
что является ответом этой задачи.

Задача 4.17

При делении 450 на нечетное число частное представляет собой простое число без остатка. Чему равно нечетное число?

Обычный подход

Обычно 450 последовательно делят на нечетные числа (1, 3, 5, …) до тех пор, пока не найдут частное в виде простого числа. Это в конечном итоге дает результат, но может потребовать довольно много времени.

Образцовое решение

Воспользуемся нашей стратегией и посмотрим на задачу с другой точки зрения. Число 450 можно записать как 2 × 32 × 52. Поскольку 32 и 52 это нечетные числа, а 450 — четное число, то единственным возможным четным простым множителем для 450 является 2. Таким образом, нечетное число равно 32 × 52 = 225.

Задача 4.18

Число 1 000 000 имеет множество пар целочисленных множителей, т.е. двух чисел, произведение которых равно 1 000 000. Однако существует только одна пара множителей, которые не содержат нулей. Чему равны эти множители?

Обычный подход

Традиционный подход — это перебор пар чисел, произведение которых равно 1 000 000, в поисках пары, не содержащей нулей. Можно начать с 1 × 1 000 000, 2 × 500 000 и т.д. Это наверняка потребует много времени — ведь у числа 1 000 000 масса пар множителей.

Образцовое решение

Проанализируем число 1 000 000 с другой точки зрения. Это число можно представить как 106. Степень, в свою очередь, можно разложить следующим образом: (2 × 5)6 = 26 × 56. Это дает нам два множителя, которые не содержат нулей: 26 = 64 и 56 = 15 625. Обратите внимание на то, что все остальные пары множителей должны содержать как минимум один ноль, поскольку при перемножении чисел 2 и 5 получается 10, а это дает число, оканчивающееся на ноль.