Глава 2. Материя
Из чего состоит мир? Как взаимодействуют между собой эти элементы?
Когда смотришь, как горит свеча или кипит вода, кажется, что вещество как будто растворяется в воздухе: свеча тает на глазах, а в кастрюле воды становится все меньше. Однако ни то ни другое вещество не исчезает, а просто меняет свое состояние. Видимый глазу воск превращается в невидимый углекислый газ и водяной пар, вода — в прозрачный пар. Материя иногда кажется эфемерной, но на самом деле она неразрушима. Химики говорят, что материю нельзя ни создать, ни уничтожить, однако здравый смысл подсказывает, что она то существует, то куда-то исчезает.
Такой бытовой взгляд на материю разделяют люди всех возрастов, но легче всего его продемонстрировать у детей. Если у вас есть знакомый дошкольник, убедитесь сами. Возьмите два прозрачных стакана: один — высокий и узкий, а другой — низкий и широкий. Налейте в низкий стакан воды до половины и покажите его ребенку. Затем перелейте воду в высокий стакан и спросите: «Воды стало больше, меньше или осталось столько же?» Столбик воды во втором стакане выше, поэтому ребенок, скорее всего, заявит, что воды теперь стало больше. Чтобы убедить ребенка в невозможном — появлении материи из ниоткуда, — достаточно просто перелить воду из стакана в стакан.
Если вы когда-нибудь проходили вводный курс психологии, возможно, вы узнали в этом нехитром фокусе задачу на сохранение Пиаже. Жан Пиаже — швейцарский психолог, в начале XX века именно он стал пионером в области исследований детского мышления. Он открыл несколько интригующих феноменов: детский реализм (ошибочное принятие видимого за реальное), детский анимизм (приписывание одушевленности неживым предметам), детский артификализм (восприятие мира как созданного руками человека) и детский эгоцентризм (предположение, что другие знают то, что знает сам ребенок). Но больше всего он прославился открытием феномена сохранения, точнее, отсутствия его у детей.

Рис. 2.1. Дошкольник скажет, что в высоком узком стакане справа (нижняя картинка) больше жидкости, чем в низком широком стакане слева (верхняя картинка), даже если он своими глазами видел, как жидкость перелили из одного стакана в другой
Есть много вариантов задач на сохранение, и маленькие дети проваливают все без исключения. Например, ребенку показывают два одинаковых по размеру глиняных шарика и просят подтвердить, что в них столько же глины, они столько же весят и занимают столько же места. (Если ребенок не согласен, его просят выровнять различие, отщипнув глины от одного шарика и прилепив к другому). После этого один шарик раскатывают в лепешку и спрашивают ребенка, содержат ли шарик и лепешка одинаковое количество глины (сохранение массы), одинаково ли они весят (сохранение веса) и занимают ли они такое же пространство (сохранение объема). Дошкольники обычно отвечают отрицательно на все три вопроса, а младшеклассники — на один или два из них. Лишь в средних классах дети начинают стабильно осознавать, что если глиняный шарик превратить в лепешку, то масса, вес и объем глины не изменятся.
Пиаже объяснял этот феномен тем, что дети еще не освоили операциональную логику, и называл их мышление «дооперациональным», полагая, что оно пронизывает не только рассуждения о сохранении, но и все аспекты их психической жизни. Выводы маленьких детей о физической причинности и их оценки моральности поведения тоже расценивались Пиаже как дооперациональные. Сегодня психология отошла от такой классификации. Выводы Пиаже вызывают сомнения по целому ряду причин. Самый главный аргумент — это то, что логические способности развиваются с разной скоростью в разных областях. В частности, дети осваивают логику естественного языка (грамматику) и логику естественных чисел (счет) еще до школы, а логику дедуктивных рассуждений (доказательств) и логику пропорционального рассуждения (дроби) — лишь через десять лет школьного обучения, да и то не всегда.
Это верно и в отношении сохранения. О сохранении массы дети узнают до сохранения веса, а о сохранении объема — в последнюю очередь. Значит, это не единое представление, которое либо приходит полностью, либо не приходит вообще, а следствие знаний о том, как определенные преобразования меняют определенные свойства определенных веществ. Раскатывание шарика глины не меняет его объема, а нагревание меняет. Если шарик нагреть, вес останется прежним, а если отправить его на Луну — изменится. Чтобы решить задачи на сохранение, нужно много знать о материи, поэтому странно использовать их для изучения когнитивного развития в целом. После Пиаже специалисты по психологии развития провели тысячи экспериментов, но я сомневаюсь, что они особенно занимались бы темой сохранения, если бы Пиаже с самого начала не подтолкнул дисциплину в этом направлении. Явления, связанные с материей, очень загадочны и разнообразны, поэтому не стоит ожидать от маленьких детей инстинктивного знания, в каких преобразованиях свойства материи сохраняются, а в каких — нет.
Материя сохраняется во многих случаях, когда на вид она совершенно явно исчезает или появляется. Это и вода, испаряющаяся из открытой емкости, и пар, поднимающийся из кипящей кастрюли, и нагретая солнцем дверь, которая перестает умещаться в раму, и сгорающие дотла бревна. При этом многие свойства материи не сохраняются при преобразованиях, которые сохраняют материю в целом. Меняется объем воды при замерзании, эластичность растянутой резинки, зернистость соли при растворении, липкость теста после выпечки. Веру дошкольников, что переливание из низкого стакана в высокий увеличивает массу воды, сложно отнести к логическим ошибкам, поскольку преобразования материи очень запутанны.
Откровенно говоря, Пиаже интересовало не только сохранение, присущее материи, но сохранение, присущее количеству в целом, в том числе численное и пространственное. Перегруппировка игрушек не меняет их числа, равно как вес глиняного шарика не меняется, если его раздавить. Пиаже хотел узнать, когда и каким образом дети приходят к неизбежности такого вывода. Последователей Пиаже ошибки сохранения увлекали и по причине своей невероятной устойчивости.
Может быть, самый прямой способ скорректировать восприятие сохранения — это научить ребенка обращать внимание на несколько параметров преобразования материи, например на распределение воды в емкости, а не только высоту ее уровня. Однако такого рода уроки мало влияют на восприятие, особенно спустя недели и месяцы. В одном из исследований несколько сотен детей проходили один из четырех видов обучения о сохранении. Одним прямо объясняли, что не так в их суждениях. Других подталкивали делать выводы еще до того, как они увидят преобразования. Третьим показывали, что преобразования легко можно обратить. Четвертым рассказывали о логических причинах, по которым при преобразованиях материи масса и объем сохраняются. После этого понимание вопросов сохранения проверяли трижды на протяжении пяти месяцев. Результаты не воодушевляли: ни один из подходов не улучшил результатов.
Интересно, что в этом и во многих других исследованиях детям в процессе обучения не рассказывали о самой материи. Пиаже объяснял подобные ошибки недостатком логического мышления, поэтому многие психологи пытались исправить положение рассказами о логике. Однако есть и другой подход: сосредоточиться на причинах сохранения, рассказать, что материальные вещества состоят из маленьких частиц и что эти частицы не могут возникать из ничего и разрушаться (если не считать ядерной реакции). Если попросить химика объяснить ребенку сохранение материи, он, скорее всего, начнет именно с молекул, а не с отношений эквивалентности и не с количественной неизменности. Этот подход действительно оказался эффективным (мы обсудим это ниже). Таким образом, спустя несколько десятилетий после того, как Пиаже объявил задания на сохранение мерой логичности детских рассуждений, мы узнали, что дети проваливают их не потому, что нелогично мыслят, а потому, что неправильно понимают природу материи.
* * *
Атомы — это составляющие материи, из которых образованы все твердые тела, жидкости и газы. «Не доверяйте атомам, — предупреждает интернет-мем. — Они во всем замешаны». Дети не видят и не ощущают атомов, поэтому даже не подозревают об их существовании. В схожей ситуации пребывало все человечество вплоть до пионерских работ ученых XIX столетия — например, Джона Дальтона, сформулировавшего принципы химического синтеза, и Джозефа Томсона, открывшего электроны. Ничто в нашем восприятии не указывает на то, что окружающая нас материя образована из каких-то частиц. В основном она представлена дискретными, связными «пакетами»: камнями, деревьями и бревнами, кирпичами, столами, стульями, ботинками, шапками, карандашами, молотками. Эти предметы не проявляют признаков молекулярного строения. Они кажутся непрерывными и целостными.
Мы не только не осознаём микроскопические компоненты макроскопических объектов, но и неправильно воспринимаем свойства самих этих объектов. Материя имеет вес и объем, но человек от природы не умеет определять их. Он может только прикинуть тяжесть (ощущаемый вес) и величину (видимый объем). В тяжести сливается собственно вес и плотность: одинаково весящие предметы будут восприниматься по-разному, если плотность у них разная (например, пятикилограммовый стальной брусок кажется тяжелее, чем пять килограммов пенопласта). Величина отличается тем, что объем в нем сочетается с площадью поверхности. Предметы с тем же объемом, но с разной площадью поверхности могут показаться разными по величине: скомканная простыня выглядит больше, чем аккуратно сложенная. Из-за своей субъективной природы тяжесть и величина меняются не так, как измеряемый вес и объем. У любой материи есть вес, но не у всякой есть ощущаемый вес (пример — снежинки и пыль). Аналогично объем есть у любой материи, но он не всегда видимый (пример — гелий и пар). Эта группа восприятий — то, что материя непрерывна, обладает тяжестью и величиной, — образует основу «холистической» теории материи, которая появляется в детском возрасте и у старших подростков сменяется «корпускулярной теорией».
Ошибки сохранения не противоречат холистической теории материи, поскольку изменение внешнего вида вещества — его высоты, ширины и площади — представляется синонимом изменения самого вещества. Однако такие ошибки не единственный пример действия холистических теорий. Они проступают и в детских суждениях о том, что является материей, а что — нет. Когда дошкольников и учеников младших классов спрашивают, состоят ли твердые предметы (например, камни, деревья, бревна и кирпичи) из материи, они единодушно отвечают утвердительно. Еще они соглашаются, что из материи состоят те нетвердые вещества, которые можно увидеть и потрогать (например, вода, соль, сок и желе). Но в том, состоят ли из материи менее осязаемые материальные вещества, например пыль, тучи, кляксы, пузыри, они уже не так уверены. Дети колеблются и в отношении видимых, но нематериальных сущностей — тени, радуги, молнии, солнечного света. Наибольшее смущение у них вызывает воздух. Они знают, что воздух их окружает, что они вдыхают его в легкие, но считают его нематериальным. Еще они утверждают, что у воздуха нет объема, то есть, например, внутри пустой коробки он не занимает вообще никакого места. Воздух противоречит самой сути детской холистической теории материи, так как имеет объем, но при этом невидим и не имеет величины, обладает весом, но неощутимым, без тяжести.
Холистические теории явно проявляются в детских предположениях о том, какие предметы пойдут ко дну, а какие — останутся на плаву. Основным фактором здесь является плотность, однако у ребенка нет органов чувств для ее оценки. Судить он может только о тяжести и величине, и это приводит к систематическим ошибкам. В одном из исследований четырехлетним малышам показывали кубики разного веса и размера и просили угадать, утонут они или нет. Большинство выбрало критерий, основанный на весе: кубики, весящие меньше 100 граммов, должны плавать, а более тяжелые — утонуть независимо от того, больше или меньше их плотность по сравнению с плотностью воды. Таким образом, прогнозы оказывались верны для легких кубиков с плотностью ниже пороговой и для тяжелых кубиков с плотностью выше пороговой, но ошибочны, если плотность легкого кубика превышала пороговую, а у тяжелого оказывалась меньше. Другие исследования показали, что детей можно побудить учитывать и вес, и размер, то есть приблизительно оценивать плотность, но сами они делают это редко. Плотность просто не проявляется в холистической теории материи.
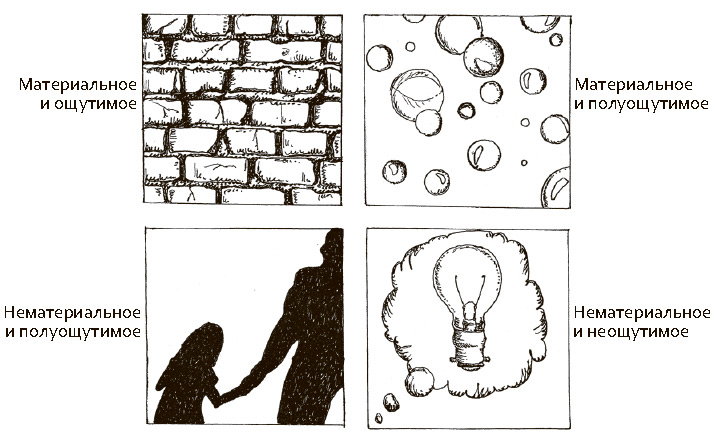
Рис. 2.2. Сначала дети определяют материю по ее ощутимости. Они правильно оценивают, что кирпичи состоят из материи, а мысли — нет, но не уверены в отношении полуощутимых сущностей, например пузырей или тени
В еще более чистой форме детские холистические теории проявлялись, когда детям предлагали поразмышлять над преобразованием материи, которое не поддается восприятию, — микроскопическим делением. Им показывали кусок пенопласта и просили представить, что произойдет с его массой, весом и объемом, если делить его напополам до бесконечности. Ниже — беседа между исследователем и третьеклассником. Именно так обычно отвечают дети младше десяти лет.
Ученый: Давай представим, что этот маленький кусочек можно разделить пополам, а потом еще раз пополам. Если мы будем его делить и делить, исчезнет ли материя пенопласта совсем?Ребенок: Да. Через год ее уже не будет. Ничего не останется.Ученый: Тогда давай представим очень маленький кусочек пенопласта — такой крохотный, что его не видно. Он будет занимать какое-то место?Ребенок: Нет, не будет. Если на столе лежит что-то очень большое, а потом убрать это в угол, оно не будет занимать никакого места.Ученый: А у такого маленького кусочка будет вес?Ребенок: Нет, тоже не будет.Ученый: Ноль граммов?Ребенок: Да. Если берешь что-то маленькое, чувствуешь только свою кожу, потому что оно ничего не весит.
Обратите внимание, что ребенок явно приравнивает объем к величине (этот крохотный кусочек можно «спрятать в угол»), а вес — к тяжести («чувствуешь только кожу»). У более старших детей результаты совершенно другие:
Ученый: Представь, что этот маленький кусочек можно раз за разом делить пополам. Если продолжать его делить, материя пенопласта когда-нибудь исчезнет окончательно?Ребенок: Половина чего-то — это тоже что-то, пусть и очень, очень маленькое. Нет такого предмета, половина которого — это ничего.Ученый: Если делить эти кусочки пополам, появится ли когда-нибудь такой фрагмент, который не будет занимать пространства?Ребенок: Нет. Сколь малой ни была бы материя, она все равно занимает какое-то место.Ученый: А получится когда-нибудь кусочек без веса?Ребенок: Вес все равно будет, пусть и неизмеримый. Если крохотный человечек попытается его поднять, он вес почувствует.
Эта шестиклассница явно считает материю неуничтожимой и наделяет весом и объемом даже малую, невидимую глазу материю. Как и ребенок в предыдущем примере, она склонна отождествлять вес с тяжестью, но признаёт, что ее собственное восприятие тяжести — точнее, отсутствия тяжести — не имеет отношения к тому, есть ли у предмета вес (отсюда отсылка к «крохотному человечку»).
Наконец, еще одно доказательство существования холистических теорий — это смущение, которое появляется у детей, когда они начинают узнавать о газах. Обычно это происходит в средней школе. В этом возрасте они уже могут согласиться с тем, что газы состоят из материи, но им все еще сложно связать макроскопические свойства газов с микроскопическими частицами. Дети поначалу воспринимают газ как целостную однородную сущность, так же, как они изначально представляли себе твердые тела. Это приводит их к отрицанию того, что частицы газа постоянно находятся в движении, разделены пустым пространством и что расстояние между ними зависит от объема, который занимает газ в целом. Некоторые взрослые тоже отвергают эти идеи. Можно многое знать о взаимосвязи между макроскопическими характеристиками твердого тела (например, плавучестью) и его микроскопическими свойствами (например, плотностью), но в случае газов все приходится осваивать заново.
* * *
Понимание детьми материи — это развитие младенческого понимания материи, хотя психологи много лет были уверены, что у младенцев отсутствует даже представление о постоянстве предметов, то есть осознание, что предметы продолжают существовать, когда на них не смотришь.
Формирование представления о постоянстве казалось медленным и растянутым процессом. До четвертого месяца жизни младенцы не пытаются тянуться к желаемому предмету, если спрятать его за ширму или под ткань. С четвертого по восьмой месяц они уже берут предмет, частично скрытый из виду, но не пытаются взять его, если он скрыт полностью. С восьмого по двенадцатый месяц дети берут полностью скрытые предметы, но при этом делают любопытную ошибку. Если предмет несколько раз спрятать в одном месте (месте A), а затем в другом (месте Б), ребенок будет искать его там, где он был спрятан раньше, и только потом переключится на новое место. Это поведение известно как ошибка А-не-Б. Наконец, с двенадцатого по восемнадцатый месяц младенцы начинают доставать предметы, скрытые из виду, независимо от того, прячут ли их туда же, куда до этого.
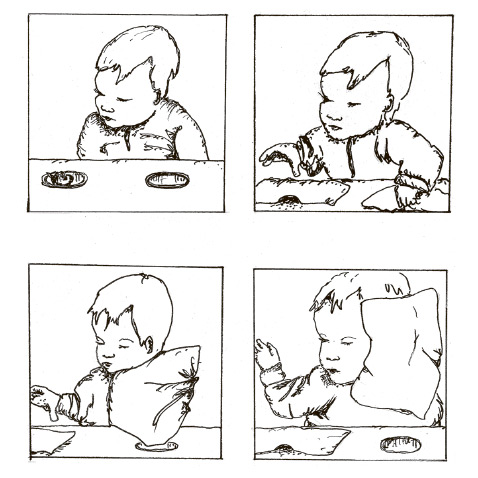
Рис. 2.3. Ребенок на рисунке ищет спрятанный предмет (накрытую игрушку) в неправильном месте (справа). Что интересно, иногда дети смотрят в правильном направлении (влево), но тянутся при этом не туда
Развитие представления о постоянстве предметов первым описал Жан Пиаже — психолог, открывший ошибки сохранения. Он пришел к выводу, что у детей нет врожденного осознания постоянства материи, не говоря уже о ее сохранении, но оно вырабатывается в течение первого года жизни. Проблема в том, что этот вывод основан на данных, в которых соединены два вида ошибок: концептуальные и двигательные. Возможно, младенцы не берут скрытые предметы не потому, что забыли об их существовании (концептуальная ошибка), а просто еще не умеют к ним тянуться (двигательная ошибка). Когда наблюдаешь за десятимесячным ребенком, совершающим ошибку А-не-Б, возникает сильное ощущение, что проблема именно в движениях, а не в восприятии: он ищет предмет не там, но смотрит часто в правильном направлении. Глаза выдают знание, которое не могут воплотить руки.
Чтобы отделить концептуальные ошибки от двигательных, можно использовать различные приемы оценки ожиданий младенцев в отношении предметов, для которых не требуется проявлять двигательные навыки. Один из них был разработан в 1970-е, в последние годы жизни Пиаже, и известен как метод зрительного предпочтения. Младенцы, как и все остальные люди, дольше смотрят на неожиданное событие (например, когда один предмет проходит сквозь другой), чем на ожидаемое (например, если предметы сталкиваются). Сравнивая таким образом уделяемое внимание, психологи узнали, что богатые и разнообразные ожидания имеются у младенцев задолго до того, как они получают возможность воплощать свои мысли на практике, не говоря уже о том, чтобы их высказывать.
В хорошо известном исследовании ученые ставили перед пятимесячными детьми прямоугольную ширму, которую можно было поворачивать вперед и назад на нижней оси. За ширму помещали маленькую коробку — так, чтобы ее не было видно, — и показывали ребенку два варианта развития событий: ширма либо останавливалась, как будто столкнувшись с преградой, либо продолжала движение, как будто проходя через нее. Наблюдая за этими событиями, взрослый удивился бы во втором случае, но не удивился в первом, и поэтому на второе событие смотрел бы дольше. Младенцы ведут себя так же. Они дольше смотрят на второе событие и, следовательно, во втором случае удивлены, а в первом — нет.
Это открытие свидетельствует не только о том, что младенцы ожидают столкновения предметов, а не прохождения их друг через друга, но и что они следят за скрытыми из поля зрения предметами, прогнозируя поведение видимых объектов (движущейся ширмы) на основе их взаимодействий с невидимыми (коробкой). Таким образом, представление о постоянстве предметов у младенцев проявляется задолго до того, как они научатся брать их руками. Уже в трехмесячном возрасте они ожидают, что спрятанная коробка остановит движение ширмы.
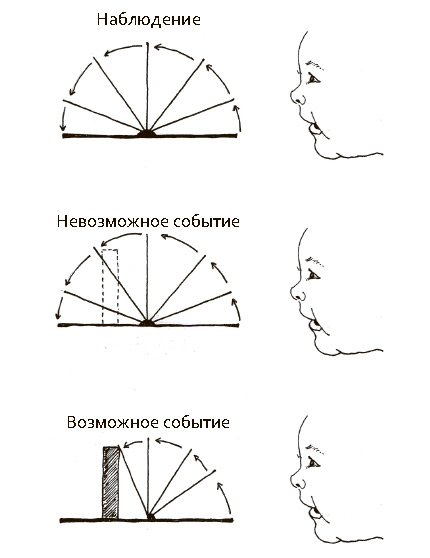
Рис. 2.4. Уже в четырехмесячном возрасте дети дольше смотрят на ширму, которая как будто проходит через твердую коробку (невозможное событие), чем на ширму, которая останавливается при контакте с коробкой (возможное событие)
Кроме того, в этом возрасте они уже считают, что предметы приходят в движение от контакта с другими предметами и описывают непрерывную траекторию. Если показать нарушения этих принципов — например, предметы, которые движутся сами по себе или возникают из ниоткуда и пропадают, — младенцы будут смотреть с недоверием. Конечно, в природе это невозможно, но хитрые ученые имитируют такие события с помощью ловкости рук и оборудования для фокусов. Таким образом, вопреки предположениям Пиаже, у младенцев есть ожидания в отношении предметов и эти ожидания сохраняются даже во взрослом возрасте. В то же время представления в отношении цельности, непрерывности и контакта проявляются только в отношении дискретных, связанных предметов и отсутствуют в случае других форм материи, например соли и песка.
В одном из исследований ученые проверяли, могут ли восьмимесячные младенцы отслеживать два вида сущностей, помещенных за непрозрачной ширмой: горку песка и предметы, похожие на горку песка, но движущиеся как единое целое (кусочки пенопласта с приклеенным песком). В первом случае ученые насыпали за ширму одну горку, а затем другую. После этого ширму опускали, показывая либо обе горки, либо всего одну. Младенцы смотрели на оба результата одинаково долго, то есть у них не было ожиданий в отношении того, сколько горок песка должно там быть. Во втором случае дети видели, как исследователи кладут за ширму один предмет, а затем второй. После этого экран опускали, показывая один либо два предмета. Теперь младенцы смотрели на один предмет значимо дольше, так как, по их мнению, за ширмой должны находиться два.
Было сделано предположение, что младенцы просто не уверены, в две или в одну горку был высыпан песок в первом случае. Именно поэтому ученые провели еще один эксперимент: насыпали песок не за одной, а за двумя ширмами, между которыми оставляли промежуток. Когда ширму опускали, показывая одну либо две горки, младенцы смотрели на оба результата одинаково долго. Они не отслеживали положение песка так, как положение цельных предметов, пусть и сделанных похожими на горку песка.
Младенцы не единственные, кто отслеживает связанные формы материи, но не отслеживает несвязанные. Когда описанные выше исследования повторили у лемуров, результаты оказались такими же: эти животные имели точные ожидания числа предметов за экраном, но не имели ожиданий в отношении горок песка.
Эволюция, видимо, не одарила приматов способностью отслеживать несвязанные вещества. Мы можем следить за предметами, которые движутся в пространстве, скрываются из виду и вступают в контакт с другими предметами, но не можем даже посчитать горки песка, по крайней мере в младенческом возрасте. Конечно, эволюция сохраняет те навыки, которые оказались полезными для выживания и размножения вида, и сложно придумать, каким образом отслеживание нетвердых веществ соответствовало бы этому критерию. Такие вещества, как молоко и вода, нужны для питания, но нет необходимости отслеживать их при перемещении в пространстве. Не обязательно и воспринимать связи между ними и другими материальными сущностями, например твердыми предметами. Представление о камне как целостном предмете, который можно поднять, перенести, бросить или спрятать, несоизмеримо важнее для выживания, чем осознание того, что камень, в сущности, аналогичен песку.
* * *
Если в начале жизни человек воспринимает материю как фундаментально целостную, то как он приходит к осознанию ее корпускулярности? Рассказывать детям, что материя состоит из частиц, не очень эффективно, потому что они еще не готовы принять эту информацию. Сначала им нужно перестроить свое понимание материи — перестать обращать внимание на отличия, важные для холистической, но не корпускулярной теории, и научиться видеть особенности, имеющие значение для корпускулярной теории, но не для холистической. В частности, детям приходится учиться игнорировать разницу между предметами и несвязанными веществами и начать рассматривать и то и другое как материю, а также увидеть различия между восприятием веса (тяжестью) и его физическим определением, между воспринимаемым объемом (величиной) и физическим термином «объем». Только после этого можно понять концепцию плотности — веса, приходящегося на единицу объема.
Плотность — это характеристика, воплощающая корпускулярную теорию. Плотным и неплотным может быть только вещество, обладающее внутренней структурой. Однако структура непроницаема для невооруженного глаза, поэтому у маленьких детей нет представления о плотности как отдельном от веса параметре. Как уже отмечалось выше, они не используют плотность для предсказания плавучести и для определения материала. Представьте себе следующее задание. Вам дали три металлических кубика: свинцовый со стороной 2,5 сантиметра и весом 180 граммов, еще один свинцовый со стороной 7,5 сантиметра и весом почти 5 килограммов и алюминиевый со стороной 13 сантиметров и весом 220 граммов. Вам нужно определить, какие кубики сделаны из одного и того же металла. Они оклеены бумагой, поэтому сориентироваться по цвету не получится.
Как вы поступите? Скорее всего, вы соотнесете вес кубиков с их величиной и поймете, что самый большой (алюминиевый) не такой тяжелый для своего размера в сравнении с двумя другими (свинцовыми). Для дошкольников и учеников младших классов эта задача оказывается на удивление сложной. Они могут определить, какой кубик выделяется с точки зрения веса, какой — с точки зрения объема, но не видят отклонений с точки зрения веса на единицу объема. Большинство детей в итоге исходят исключительно из веса кубиков, сравнивая меньший свинцовый с алюминиевым.
Эту задачу с угадыванием материала придумали психолог Кэрол Смит и ее коллеги. Она уже более трех десятилетий изучает детские интуитивные теории материи. Большинство ее исследований посвящено плотности, так как это хороший показатель понимания детьми материи в целом. Один из придуманных Смит способов объяснить детям понятие плотности — массы на единицу объема — заключается в сравнении этого неуловимого параметра с удельными количествами, поддающимися восприятию. Давление, например, это удельный параметр (сила на единицу площади), который можно почувствовать кожей, а темп — удельный параметр (число ударов на единицу времени), который можно услышать. Концентрация — удельный параметр (число молекул в единице объема), определяемый языком, а насыщенность (число предметов на единицу площади) — удельный параметр, видимый глазу.
В одном из исследований Смит вводила понятие плотности с помощью двух других удельных концепций: концентрации и насыщенности. Чтобы научить семиклассников выделять переменные, входящие в удельные величины, им предлагали расследовать два гипотетических убийства. В первом случае жертва выпивала отравленный напиток Kool-Aid, и детям нужно было определить, кто из подозреваемых его приготовил. Для этого требовалось сравнить между собой концентрации продуктов в любимых рецептах у всех подозреваемых, то есть количество порошка на единицу воды. Во втором случае жертву отравляли печеньем с кусочками шоколада, и дети должны были определить, кто его испек. Они сравнивали насыщенность печенья шоколадом в рецептах подозреваемых, то есть количество кусочков шоколада на единицу теста.
Чтобы оценить понимание испытуемыми концентрации, насыщенности и плотности, Смит просила расположить в порядке увеличения растворы разной концентрации, различную насыщенность точек и материалы разной плотности. Все удельные величины определялись легко вычисляемыми параметрами: например, четыре чайные ложки сахара на два стакана воды. Перед экспериментом с расследованием убийства ученики уже умели располагать точки по насыщенности, но не умели располагать растворы по концентрации и материалы по плотности. После эксперимента они могли расположить растворы, но все еще не материалы. Понятийный промежуток между отрабатываемыми величинами (насыщенностью и концентрацией) и целевой величиной (плотностью) оказался слишком велик.
В дальнейших исследованиях Смит и коллеги применили другой подход. Вместо того чтобы пытаться сделать плотность воспринимаемым параметром, они показывали ученикам материальные явления, объяснимые только с точки зрения плотности и ее составных элементов — веса и объема. Несколько недель ученики взвешивали на очень чувствительных весах маленькие, не имеющие тяжести предметы (блестки, капли чернил). На рычажных весах они сравнивали пустые воздушные шары с шарами, наполненными воздухом. Они определяли объем предметов, которые не получается измерить линейкой (капли воды), исходя из измеримых объемов (миллилитр воды). Они погружали предметы разной плотности в жидкости разной плотности. Они измеряли вес и объем железного шарика до и после нагревания и вес таблеток шипучего аспирина до и после растворения в воде.
В отличие от задач с убийствами, этот подход оказался эффективным. До курса лишь немногие ученики могли упорядочить материалы по плотности. После курса с этим справлялось большинство. Кроме того, после курса большинство учеников начало считать материей неосязаемые вещества (воздух, пыль, дым) и приписывать вес микроскопическим объектам (крохотному кусочку пенопласта). Наверное, больше всего заслуживает внимания тот факт, что ученики, сначала провалившие задачи Пиаже на сохранение, после обучения справлялись с ними, хотя тема сохранения прямо не затрагивалась.
Дополнительные исследования группы Кэрол Смит показали, что освоение корпускулярной теории материи имеет на удивление обширные последствия за пределами области материи, в мире чисел. Целые числа, как и предметы, можно делить на меньшие составляющие (дроби), однако дети изначально воспринимают числа по-другому, считая их просто конечными точками отсчета. Малыши понимают, что числа можно увеличивать и уменьшать, прибавляя и убирая предметы, но не имеют представления о делении. Числа рассматриваются как целостные и однородные, аналогичные физическим объектам.
Заинтригованные этим сходством, Смит и коллеги задались вопросом, развивается ли понимание делимости чисел в тандеме с пониманием делимости материи. Для этого они совместили описанную выше задачу на деление пенопласта с задачей на деление чисел. Вот простой пример беседы с третьеклассником:
Ученый: Между нулем и единицей есть еще какие-нибудь числа?Ребенок: Нет.Ученый: А половина?Ребенок: Да. Получается, что есть.Ученый: А сколько примерно чисел между нулем и единицей?Ребенок: Ну, не очень много. Только ноль и половина, потому что это на полпути к единице.Ученый: Давай представим, что ты разделил два пополам и получил один, а затем снова разделил результат пополам. Можно так делить до бесконечности?Ребенок: Нет, потому что если взять эту половину числа, получится ноль, а ноль разделить нельзя.Ученый: То есть когда-нибудь получится ноль?Ребенок: Да.
Некоторые дети знали, что существуют и другие дроби, не только одна вторая. Один третьеклассник, например, заметил: «Есть половина, треть, четверть, одна какая-то и так далее вплоть до десяти». Но даже такие дети отрицали, что сами эти дроби можно делить. В более старшем возрасте дети уже не просто утверждали, что дроби, например одну четверть, можно разделить пополам, но и что делить пополам можно бесконечно. Это иллюстрирует следующий диалог с пятиклассником:
Ученый: Между нулем и единицей есть еще какие-то числа?Ребенок: Да, есть.Ученый: Можешь привести пример?Ребенок: Одна вторая или ноль целых пять десятых.Ученый: А сколько примерно чисел между нулем и единицей?Ребенок: Много.Ученый: Представь, что ты разделил два пополам, получил единицу и опять разделил ее пополам. Можно так делить до бесконечности?Ребенок: Да. Когда что-то делишь, всегда что-то остается.Ученый: Ты когда-нибудь получишь ноль?Ребенок: Нет, потому что есть бесконечно много чисел меньше единицы, но больше ноля.
Крайне важно то, что осознание детьми делимости чисел сопровождает осознание делимости материи. Дети, утверждающие, что числа на каком-то шаге деления перестают существовать, согласны и с тем, что материальные вещества в какой-то момент деления теряют вес, в то время как дети, несогласные с первым утверждением, не согласны и со вторым. И тем не менее, если понимание приходит не одновременно, отстает именно представление о бесконечной делимости чисел, то есть бесконечную делимость материальных сущностей (предметов) дети усваивают раньше бесконечной делимости нематериальных (чисел).
Понимание строения материи, таким образом, может стать трамплином к более сложному пониманию чисел. Бесконечная делимость, как и бесконечная плотность, — очень важная идея, которую можно перенести из одной области в другую. Подчеркивание параллелей между этими явлениями — очень продуктивная стратегия преподавания натуральных дробей и других видов рациональных чисел, например десятичных дробей и процентов. Ученики, которых учили ассоциировать дроби с долей емкости, заполненной водой (веществом), успевают намного лучше, чем те, которым дроби показывали в виде кусков пирога (предмета). Предметы бывают полезны при освоении целых чисел, так как и то и другое дискретно, связано и едино, но дроби лучше объяснять на примере веществ, так как и то и другое непрерывно, делимо и обладает плотностью. Параллели между числами и материей проходят глубже, чем в самих этих областях.
* * *
Что тяжелее: килограмм пуха или килограмм золота? Конечно, ни то ни другое: килограмм и есть килограмм. Но вполне вероятно, что перед тем, как ответить на этот вопрос, вы на секунду задумались. Золото «весомее» пуха, и концепция тяжести вступает в противоречие с концепцией веса. Тяжесть и величина — это воспринимаемые качества материи. Они сохраняются при изменениях ее концептуального понимания и мешают рассуждать о материальных явлениях на протяжении всей нашей жизни.
Возьмем задачу о том, какой предмет утонет, а какой — нет. Взрослые быстро оценивают, что большие плотные предметы, например сковородка, идут ко дну, а легкие и воздушные, например упаковочный пенопласт, остаются на поверхности. Однако сравнить легкий, но при этом плотный предмет, например железную стружку, с тяжелым, но воздушным, например пенопластовой коробкой, уже сложнее. Даже если человек признает, что плотность — единственный параметр, имеющий отношение к задаче, тяжесть и величина все равно вмешиваются в рассуждения.
Тяжесть и величина нарушают и способность отделять материальные сущности от нематериальных. Если попросить человека быстро классифицировать «материальное» и «нематериальное», неощутимые вещества (чернильные пятна, духи, воздух) потребуют больше времени, чем ощутимые (камни, кирпичи, ботинки). Ошибки будут совпадать с детскими ошибками в аналогичных заданиях без ограничения времени. В одном из исследований скоростной классификации взрослые относили чернильные пятна к материи лишь в 85% случаев, духи — в 83%, а воздух — в 75%. И наоборот, в 35% случаев к материи причисляли гром, в 37% — свет звезд, а в 57% — молнию. Даже Антуан Лавуазье, основоположник современной химии, был сбит с толку физической сущностью тепла и света. И то и другое он отнес к элементам материи.
Чтобы сбиться в рассуждениях о материи, не обязательно нужна нехватка времени. Люди ошибаются и в обычных ситуациях. Например, мы ставим заполненную до краев бутылку воды в холодильник, забывая, что она лопнет, когда вода внутри расширится. Мы переплачиваем за большие упаковки продуктов, не задумываясь об эквивалентности количества на единицу упаковки в товарах разных размеров. Мы перенапрягаемся, расчищая снег с дорожки, не осознавая, что скопление не имеющих тяжести снежинок — это десятки килограммов замерзшей воды. А еще мы не можем разобраться, наполовину пуст стакан или наполовину полон, хотя в действительности он заполнен целиком — отчасти жидкостью и отчасти газом.
Мой любимый бытовой пример ошибок, связанных с материей, — это разливное пиво в пабе. Стандартный стакан на пинту — 0,47 литра — размером 14,9 сантиметра в высоту, 8,2 сантиметра в диаметре сверху и 6 сантиметров в диаметре у донышка. Сколько пива, по-вашему, будет не хватать, если на глазок налить стакан не до краев, а до высоты 12,7 сантиметра?
Почти четверти объема! Ведь стакан сужается книзу и в его верхней части умещается больше пива, чем в нижней. Большинство забывают, сколько пива упускают из-за недолива, но теперь решение проблемы найдено. Предприимчивые любители пива изобрели карманный прибор для измерения уменьшения объема пива в зависимости от высоты. Его название хорошо отражает происхождение идеи: пивоизмеритель Пиаже.

Рис. 2.5. Бытовых ошибок на сохранение очень много даже у взрослых. Хороший пример — хроническое неумение оценить, сколько пива не хватает в неполном стакане
Назад: Часть I. Интуитивные теории физического мира
Дальше: Глава 3. Энергия

