Глава четвертая. Дзета-гипотеза Римана и смех простых чисел

Какой будет цивилизация через миллион лет? Почти все, к чему мы привыкли, к тому времени исчезнет. Но кое-что останется. И в том числе числа и смех, тут можно не сомневаться. Это хорошо, поскольку числа и смех придают смысл жизни – конечно, по-разному, но все же. Поэтому интересно поразмышлять, каков будет их статус в миллионном году. Но вначале позвольте пояснить, почему я так уверен, что они никуда не денутся, если почти все, что нам сегодня известно, либо исчезнет, либо изменится до неузнаваемости.

В целом все, что существует уже давно, скорее всего, просуществует еще гораздо дольше. А вот всякого рода новинки – вряд ли. И то, и другое следует из принципа Коперника, который, в сущности, говорит, что в нас нет ничего особенного. А поскольку и в нашей точке зрения нет ничего особенного, нам едва ли удастся застать тот или иной феномен в самом начале или в самом конце существования. Вот, скажем, вы идете на бродвейский мюзикл. Сколько он продержится на сцене, не знает никто: все может обернуться как угодно, от нескольких дней до десятков лет. Однако вы точно знаете, что из всех, кто его посмотрит, 95 % не попадут ни в число первых 2,5 %, ни в число последних 2,5 %. Следовательно, если в вас нет ничего особенного, то есть вы просто случайный зритель из числа всех зрителей представления, можете быть на 95 % уверены, что не попадете в эти «хвосты». Это значит, что если спектакль шел уже n раз на тот момент, когда вы собрались его посмотреть, можете быть на 95 % уверены, что впереди у него не больше 39×n и не меньше n: 39 представлений. (Простая арифметика: верхний предел не допускает вас в число первых 2,5 % всех зрителей, а нижний – в число последних 2,5 %.) Так что, заручившись всего лишь принципом Коперника и школьной арифметикой, вы можете определить ожидаемую продолжительность жизни, скажем, бродвейского спектакля с точностью до 95 %. Потрясающе.

Эту логическую цепочку придумал Дж. Ричард Готт III, астрофизик из Принстонского университета. В 1993 году он опубликовал в журнале «Nature» статью «Как принцип Коперника влияет на наши перспективы» (Gott III, J. R., «Implications of the Copernican Principle for Our Future Prospects»), где рассчитал ожидаемую продолжительность жизни нашего вида. Люди существуют уже около 200 000 лет. Поэтому, если момент, в который мы наблюдаем наш вид, ничем особенным не выделяется, можно быть на 95 % уверенными, что он просуществует еще не менее 5100 лет (1/39×200 000), но исчезнет за 7,8 миллионов лет (39×200 000). Готт отмечает, что это обеспечивает виду homo sapiens ожидаемую продолжительность существования, сопоставимую с другими видами гоминид (наш предок Homo erectus просуществовал 1,6 миллион лет) и млекопитающими в целом (у них средняя продолжительность существования вида около 2 миллионов лет). Кроме того, это дает нам достаточные основания считать, что в миллионном году мы никуда не исчезнем, хотя эта вероятность не так велика, как мы по наивности надеемся (см. «Конец близок», стр. 322).

А что тогда будет, кроме нас? Вспомните что-нибудь, что появилось совсем недавно, скажем, Интернет. Интернет существует около трети столетия (об этом я узнал, заглянув в тот же Интернет, в «Википедию»). Согласно логике Коперника, мы можем быть на 95 % уверенными, что он просуществует еще 10 месяцев, но исчезнет самое большее через 300 лет. Так что в миллионном году почти наверняка не будет ничего даже отдаленно похожего на Интернет (пожалуй, не то чтобы сенсационный вывод). То же самое можно сказать и о бейсболе, существующем чуть больше двухсот лет. И о технологии промышленного производства, которая появилась всего несколько сотен лет назад и, скорее всего, в ближайшие десять тысяч лет уступит место чему-то новому и невиданному. По той же коперниковской логике не стоит делать ставки и на то, что в миллионном году сохранится что-то похожее на официальную религию.

Как ни парадоксально, но если мы хотим найти что-то, что с большой вероятностью сохранится к миллионному году, нам придется возвращаться в своей естественной истории гораздо глубже в прошлое. Ведь, по выражению Готта, «что уже долго было, то долго и продержится». И если мы заглянем в прошлое на несколько миллионов лет, то в числе прочего увидим смех и числа.

Откуда мы это знаем? В наши дни и смех, и числовое чутье у нас общее с другими видами, а значит, они были и у наших общих предков, существовавших миллионы лет назад.

Вот, скажем, смех. Шимпанзе умеют смеяться. Чарльз Дарвин отмечает в книге «О выражении эмоций у человека и животных» (1872): «Если щекотать молодого шимпанзе (у них особенно чувствительна к щекотанию, как у наших детей, подмышечная область), то он издает более определенный звук, похожий на хихиканье и смех; впрочем, смех иногда бывает беззвучен» (пер. под ред. Е. Павловского). На самом деле то, что в приматологии называют смехом шимпанзе, ближе к сиплому пыхтению. Оно проявляется не только при щекотке, но и при шуточной борьбе, игре в догонялки и притворных атаках – точь-в-точь как у детей до появления словесных шуток в возрасте пяти-шести лет. Но выходят ли шутки приматов за границы чисто физических проявлений? Исследователь Роджер Футс рассказывал, что шимпанзе Уошо, которая умела изъясняться языком жестов, как-то раз, когда он посадил ее себе на плечи, помочилась на него, после чего показала знак «смешно» и фыркнула, но не засмеялась.

Линии людей и шимпанзе разошлись пять-семь миллионов лет назад. Если сделать резонное предположение, что смех у людей и шимпанзе «гомологичен», а не возник независимо, это значит, что смеху тоже не меньше пяти-семи миллионов лет. Поэтому, согласно принципу Коперника, смех в миллионном году, скорее всего, сохранится.

Теперь рассмотрим числа. Шимпанзе умеют и производить элементарные арифметические вычисления, и их учили применять символы, похожие на цифры, чтобы рассуждать о количестве. Числовое чутье свойственно не только приматам. Исследователи обнаружили, что воспринимать и выражать числа способны самые разные животные – саламандры, дельфины, еноты. Лет двадцать назад ученые из Массачусетского технологического института обнаружили, что у макак есть специализированные числовые нейроны в той части мозга, которая у людей соответствует зоне, отвечающей за числа. Очевидно, у числового чутья давняя эволюционная история, оно даже древнее смеха. Следовательно, по тому же принципу Коперника можно быть уверенными, что в миллионном году числа никуда не исчезнут.

Числа и смех – одни из древнейших культурных чудес нашего мира. Поэтому они, скорее всего, просуществуют дольше всех и, весьма вероятно, переживут и миллионный год. Здесь можно провести аналогию с семью чудесами света, о которых говорили в античности. Когда этот список был составлен (самая ранняя версия датируется примерно 140 годом до н. э.), древнейшим чудом света с большим опережением были египетские пирамиды (около 2500 лет до н. э.). А остальные чудеса – висячие сады Семирамиды, храм Артемиды в Эфесе, статуя Зевса в Олимпии, мавзолей в Галикарнасе, Колосс Родосский и Александрийский маяк – были моложе почти на две тысячи лет. Какое из семи чудес сохранилось до наших дней? Правильно, пирамиды. Остальные исчезли – погибли при пожарах и землетрясениях.

Ожидаемая продолжительность жизни смеха и чисел – как у пирамид. И это, как я уже говорил, хорошо, поскольку они лежат в основе юмора и математики соответственно, и это помогает жить самым возвышенным душам среди нас. Бертран Рассел в автобиографии рассказывает, что в юности был несчастен и часто задумывался о самоубийстве. Но дальше размышлений дело не пошло, поскольку, признается он, «мне хотелось побольше узнать о математике». Такие же суицидальные настроения одолевают и героя Вуди Аллена в фильме «Ханна и ее сестры», но он отходит от опасной грани, когда случайно заглядывает в кино и видит, как братья Маркс в фильме «Утиный суп» выстукивают мелодию на шлемах фридонских солдат, будто на ксилофоне. Чтобы жизнь наших потомков из миллионного года стоила того, чтобы жить, пусть лучше у них останутся смех и математика.

Но какой она будет, их математика? И над чем они станут смеяться?

Ответить на первый вопрос, пожалуй, проще. Ведь математика – самая универсальная часть человеческой цивилизации. Все земные культуры умеют считать, следовательно, во всех земных культурах есть понятие о числе. Если где-то в космосе существует разумная жизнь, мы вправе ожидать от нее чего-то подобного. Единственный универсальный признак цивилизации, который узнают где угодно по всей Вселенной, – это число. В фантастическом романе Карла Сагана «Контакт» инопланетяне из окрестностей Веги отправляют на Землю последовательность простых чисел. Героиня книги, которую в экранизации «Контакта» играет Джоди Фостер, работает в SETI (программе поиска внеземных цивилизаций). И к вящему своему восторгу и ужасу понимает, что простые числа, которые улавливает ее радиотелескоп, генерирует какая-то разумная жизнь.

Но что было бы, если бы инопланетяне отправили нам не числа, а шутки? Скорее всего, мы не отличили бы их от фонового шума. Ведь мы с трудом отличаем от фонового шума даже шутки из шекспировских пьес (нет, правда, вам когда-нибудь бывало по-настоящему смешно на шекспировской пьесе?) Нет ничего более вечного, чем число, основа математики, – но нет ничего более узкого и эфемерного, чем юмор, основа смеха. По крайней мере, нам так думается. Мы совершенно уверены, что цивилизация, на миллион лет опередившая нас в развитии, согласится с нашим понятием о числе, а мы – с их. Однако от их шуток мы, скорее всего, только растерянно почесали бы в затылке – и наоборот. Что же касается всех промежуточных явлений культуры, от литературы на самом эфемерном конце континуума до философии и физики на самом универсальном – кто знает?..

Так видится нам картина сегодня. Но в миллионном году, полагаю, она будет прямо противоположной. Самым универсальным аспектом культуры будет считаться юмор. А число растеряет трансцендентную репутацию и превратится в сугубо местный артефакт вроде компьютерной операционной системы или формы бухгалтерской отчетности. Если я прав, ученые из SETI будут высматривать в сигналах не простые числа и не цифры числа p, а что-то совсем другое.

Но вернемся ненадолго к числам. В 1907 году Бертран Рассел, которому было за тридцать, написал настоящий гимн во славу математики. «Математика, при правильном на нее взгляде, обладает не только истинностью, но также высшей красотой – красотой холодной и строгой, подобной красоте скульптуры, которая не прибегает ни к одной из более слабых частей нашей природы, которая не использует эффектных внешних украшений, свойственных живописи или музыке, и, тем не менее, – возвышенно чистой и способной к тому суровому совершенству, которое может демонстрировать лишь величайшее искусство» (здесь и далее пер. В. Шапошникова). Эти строки, подчеркивающие трансцендентный образ математики, часто цитируются в популярной литературе о математике. Однако в таких книгах нечасто встретишь ссылки на совсем иную точку зрения, которую Рассел высказывал, когда ему было под девяносто и он уже отмел свои юношеские панегирики (или почти юношеские), назвав их «по большей части чушью». Математика, писал пожилой Рассел, «перестала казаться мне нечеловеческой с точки зрения ее содержания. Я пришел к убеждению, хотя и крайне неохотно, что она состоит из тавтологий. Боюсь, что разуму, обладающему достаточной интеллектуальной силой, вся математика покажется тривиальной, как тривиально утверждение, что четвероногое животное есть животное». Так что на протяжении жизни представления о математики у Рассела сильно эволюционировали. И мне кажется, что к миллионному году вся наша цивилизация претерпит такие же изменения (да, Вирджиния, филогенез иногда повторяет онтогенез). Для наших потомков математика станет всего лишь сложной системой тавтологий, сугубо местного значения, которая оказалась для нас удобным инструментом вроде бухгалтерской системы, позволяющим наладить отношения с окружающим миром.

Если математика, в сущности, тривиальна, ее тривиальность должна быть особенно очевидной на элементарном уровне, пока дым и зеркала высших теорий еще не сделали свое дело. Что ж, давайте рассмотрим этот уровень.

Никто не станет спорить, что самые фундаментальные объекты математики – это положительные целые числа: 1, 2, 3 и так далее. Особое место среди этих чисел должны занимать простые числа, те самые, которые направляли на Землю инопланетяне в «Контакте». Простое число – это число, которое нельзя разложить на меньшие множители (то же самое можно сказать иначе: простое число – это число, которое делится только само на себя или на единицу). Первые простые числа – это 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37… Простые числа – это атомы арифметики, а все остальные числа называются составными, и их можно получить, перемножив простые в разных сочетаниях. Так, чтобы получить число 666, нужно перемножить 2×3×3×37. Можно без особых усилий доказать, что любое составное число можно разложить на простые множители одним и только одним способом. Это часто называют основной теоремой арифметики.

Пока что все сходится: одни тавтологии. Так что перейдем к следующему очевидному вопросу: а сколько их, этих простых чисел?

Этот вопрос задал еще Евклид в III веке до нашей эры, и ответ содержится в предложении 20 книги IX его «Начал»: простых чисел бесконечно много. Доказательство этого предложения, которое приводит Евклид, – пожалуй, первое по-настоящему элегантное рассуждение в истории математики. Оно укладывается в одну фразу: если бы простых чисел было конечное множество, то можно было бы перемножить их все, прибавить единицу и получить новое число, которое не делится ни на одно простое число, а это противоречие. (Новое число делилось бы с остатком 1 на любое число из якобы конечного списка простых, так что оно либо само было бы простым числом, либо делилось бы на какое-то простое число, не вошедшее в список. Так или иначе, изначальный конечный список простых чисел оказался бы неполным. Значит, не существует конечного списка, который охватил бы все простые числа. Следовательно, их бесконечно много).

Итак, мы знаем, что ряд простых чисел тянется бесконечно. Но тогда естественным образом возникает следующий вопрос: как эти атомы арифметики разбросаны среди всех прочих чисел? Есть ли какая-то закономерность? Среди относительно небольших чисел простые попадаются довольно часто, но чем дальше уходишь по числовой оси, тем они реже. Четыре из первых десяти чисел простые (2, 3, 5 и 7). Из первых 100 чисел простых 25. Если немного перепрыгнуть вперед, окажется, что между 9 999 000 и 10 000 000 девять простых чисел, из следующей сотни, от 10 000 000 до 10 000 100, – только два (10 000 019 и 10 000 079). Можно найти сколь угодно длинные отрезки числовой оси, где простых чисел вовсе нет. Но есть и очень большие простые числа, стоящие по соседству, например, 1 000 000 009 649 и 1 000 000 009 651. (Простые числа, отличающиеся всего на 2, называются числами-близнецами; конечно или бесконечно их количество, вопрос открытый.) Такое ощущение, что простые числа рассыпаны практически случайно, словно сорная трава среди остальных чисел. «Похоже, нет никаких причин, по которым одно число простое, а другое нет, – объявил математик Дон Цагир на инаугурационной лекции в Боннском университете в 1975 году. – Напротив, если посмотреть на эти числа, складывается впечатление, что перед тобой необъяснимая тайна бытия».

Простые числа, несмотря на свое несложное определение, видимо, живут в своей вечной и сложной реальности, независимой от нашего сознания. Они обладают трансцендентной загадочностью, той самой, которой начисто лишено высказывание Рассела «четвероногое животное – это животное». Но неужели они не подчиняются совсем никаким законам? Это было бы неожиданно, учитывая их роль строительного материала арифметики. И на самом деле у них есть свой закон. Но для того, чтобы его обрести, нужно, как ни странно, подняться на много этажей в небоскребе математики – от скромных натуральных чисел через целые, дроби, действительные числа до самых комплексных чисел с мнимой частью. (Исторически это восхождение заняло больше двух тысяч лет). И вот тогда, на самом-самом верху, мы и наталкиваемся на головоломку, которая называется дзета-гипотезой Римана.

∞

Практически все математики согласны, что дзета-гипотеза Римана – величайшая нерешенная задача во всей математике. Вероятно, это самая сложная задача, порожденная разумом человека. Риман – это Бернхард Риман, немецкий математик, живший в XIX веке. Дзета – это дзета-функция, творение высшей математики, которая, как первым установил Риман, таит в себе тайну простых чисел. В 1859 году Риман в краткой, но невероятно глубокой статье сформулировал гипотезу о дзета-функции. Если эта гипотеза верна, то простые числа подчиняются скрытой гармонии, причем довольно красивой. Если ложна, мелодия простых чисел несколько неблагозвучна – словно ее играет расстроенный оркестр.

Как же все обстоит на самом деле? Последние полтора века математики тщетно пытались доказать дзета-гипотезу Римана. Давид Гильберт включил ее в список из 23 важнейших задач математики в своей знаменитой речи на математической конференции в 1900 году в Париже (а позднее объявил, что это важнейшая задача «не только математики, а вообще»). Гипотеза Римана была единственной из списка Гильберта, которая так и осталась нерешенной за целых сто лет. В 2000 году, в столетнюю годовщину речи Гильберта, группа ведущих математиков планеты провела пресс-конференцию в Колледж де Франс и назвала новый набор из семи «Задач тысячелетия», за решение любой из которых назначалась награда в миллион долларов. (Призовой фонд обеспечивает Математический институт Клэя, основанный бостонским инвестором Лэндоном Т. Клэем.) Никого не удивило, что гипотеза Римана попала и в этот список.

Дзета-гипотеза Римана – не просто ключ к пониманию природы простых чисел. Она настолько важна для математического прогресса, что заранее считается истинной (вероятно, опрометчиво) в предварительных доказательствах тысяч теорем (которые, как говорят математики, «обусловлены» этой гипотезой). Если она окажется ложной, рухнет целая область высшей математики, построенная на ней. (Великая теорема Ферма, доказанная в 1995 году, не играла в математике такой структурной роли и поэтому значительно менее важна.)

Естественно, происхождение у дзета-функции музыкальное. Если ущипнуть скрипичную струну, она при вибрациях порождает не только ноту, на которую настроена, но и все возможные обертоны. Математически эта комбинация звуков соответствует бесконечной сумме ζ(s)=1+(1/2)'+(1/3)'+(1/4)'+…, которая называется гармоническим рядом. Если взять каждый член этого ряда и возвести его в степень s, получится дзета-функция от переменной s:

Эту функцию придумал около 1740 года Леонард Эйлер, который затем сделал замечательное открытие. Он обнаружил, что дзета-функция, бесконечная сумма, проходящая через все числа, может быть записана как бесконечное произведение, проходящее только через простые числа, которые появляются в виде обратных величин:

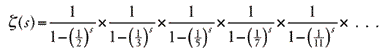
Эйлер был величайшим математиком своего времени, но и он не вполне осознал потенциал открытой им формулы бесконечных произведений. «До сегодняшнего дня математики тщетно пытались выявить какой-то порядок в последовательности простых чисел, – писал Эйлер, – и у нас есть причины полагать, что это тайна, в которую человеческий разум никогда не проникнет».

Полвека спустя Карл Фридрих Гаусс сделал первый настоящий прорыв в понимании простых чисел со времен Евклида. Мальчиком Гаусс обожал подсчитывать, сколько простых чисел содержится в каждом отрезке по тысяче. Такие размышления были приятным способом скоротать «скучные четверть часа, – писал он другу, – но потом я бросил это занятие, не добравшись и до миллиона». В 1792 году, в пятнадцать лет, Гаусс заметил интересную закономерность. Хотя на первый взгляд простые числа располагались на числовой оси в случайном порядке, в их потоке в целом все же нашлась некоторая регулярность. Можно было достаточно точно оценить, сколько простых чисел встретится до данного числа, разделив данное число на его натуральный логарифм. Представьте себе, к примеру, что вы хотите узнать, сколько простых чисел найдется до миллиона. Достаньте карманный калькулятор, наберите на нем 1 000 000 и разделите на ln(1 000 000). Получится 72 382. На самом деле простых чисел до миллиона 78 498, поэтому оценка ошибочна примерно на 8 %. Однако при увеличении заданного числа погрешность стремится к нулю.

Гаусс открыл «монетку, которую бросает Природа, чтобы выбрать простые числа» (по словам британского математика Маркуса дю Сутоя). Было что-то немного жуткое в том, что эту монетку надо взвешивать натуральным логарифмом, который родился в непрерывном мире дифференциального исчисления и, казалось бы, не имеет никакого отношения к прерывистому миру натуральных чисел (логарифмическая функция определяется площадью под определенной кривой). Гаусс не смог доказать, что натуральная логарифмическая функция в дальнейшем предскажет, что на бесконечности простых чисел становится все меньше и меньше – он просто высказал эмпирическую догадку. Не смог он и объяснить ее приблизительность – почему она не в состоянии точно сказать, где находится следующее простое число.

За завесу мнимой случайности удалось заглянуть лишь Риману. В 1859 году в статье, в которой было меньше 10 страниц, он сделал несколько ходов, которые разгадали загадку простых чисел. Начал он с дзета-функции. Эйлер считал, что эта функция охватывает только действительные числа (в множество действительных чисел, соответствующих точке на числовой прямой, входят целые числа, как положительные, так и отрицательные, рациональные числа, выражаемые дробями, и иррациональные числа вроде π или е, выражаемые непериодическими десятичными дробями). Однако Риман пошел дальше Эйлера и обобщил дзета-функцию на множество комплексных чисел.

Комплексные числа состоят из двух разных частей – действительной и мнимой (в мнимую часть входит квадратный корень из минус единицы). Типичное комплексное число – например, 2+3√-1, где 2 – действительная часть, а 3√-1 – мнимая. Поскольку у комплексного числа две части, его можно представить себе как двумерное: в отличие от действительных чисел, они располагаются не на числовой оси, а на плоскости. Риман решил распространить дзета-функцию на комплексную плоскость. И показал, что в каждой точке комплексной плоскости дзета-функция задает высоту. Она порождает обширный абстрактный ландшафт с горами, холмами, долинами и равнинами, которые тянутся бесконечно во все стороны – дзета-ландшафт. А самые интересные точки дзета-ландшафта, как обнаружил Риман, – это точки, где высота равна нулю, то есть на уровне моря. Эти точки называются нулями дзета-функции, поскольку соответствуют тем комплексным числам, которые, если подставить их в дзета-функцию, дают нуль. Эти комплексные «нули» дзета-функции, которых на дзета-ландшафте бесконечно много, позволили Риману совершить настоящее чудо: он впервые в истории вывел формулу, которая точно описывала, как бесконечное множество простых чисел располагается в числовой последовательности.

Это открытие послужило началом метафорического диалога между математикой и музыкой. До Римана в простых числах слышался лишь случайный шум. Теперь появился новый способ услышать их мелодию. Каждый нуль дзета-функции, входящий в римановскую формулу простых чисел, порождает волну, напоминающую чистый музыкальный тон. Если сочетать все эти музыкальные тоны, они порождают гармоническую структуру простых чисел. Риман обнаружил, что положение данной нулевой точки на дзета-ландшафте определяет высоту и громкость соответствующей музыкальной ноты. Чем дальше нуль к северу, тем выше звук. А главное – чем дальше он к востоку, тем громче. Оркестр простых чисел играет в гармонии, так, чтобы ни один инструмент не заглушал соседей, только если все нулевые точки лежат в достаточно узкой полосе долготы на дзета-ландшафте. Но Риман пошел еще дальше. Разведав лишь крошечный клочок бесконечного дзета-ландшафта, он смело предположил, что все нули лежат вдоль критической линии, проходящей с юга на север. И это утверждение впоследствии и получило название дзета-гипотезы Римана.

«Если гипотеза Римана истинна, – писал дю Сутой, – она объяснит, почему мы не наблюдаем строгой закономерности в расположении простых чисел. Закономерность соответствует точкам, где какой-то инструмент играет громче остальных. Как будто каждый инструмент играет свою закономерность, но при таком совершенном сочетании закономерности гасят друг друга, и остается только бесформенный поток простых чисел, которые то прибудут, то схлынут». Есть что-то волшебное в том, как бесконечное множество нулевых точек на дзета-ландшафте коллективно контролирует размещение бесконечного количества простых чисел среди натуральных: чем сильнее регламентировано расположение нулей по одну сторону зеркала, тем случайнее кажется порядок простых чисел по другую.

Но так ли идеально регламентированы нули, как думал Риман? Если гипотеза Римана ложна, ее опровергнет один-единственный нуль, сместившийся с критической линии. А вычислить, где расположены нули, задача нетривиальная. Когда сам Риман разведывал дзета-ландшафт, то обнаружил, что первые несколько точек на уровне моря выстроились именно так, как он рассчитывал. В начале XX века вручную рассчитали расположение еще нескольких сотен нулей. С тех пор компьютеры локализовали миллиарды нулей – и все они расположены точно на критической линии. Казалось бы, раз до сих пор не удалось найти контрпримера гипотезы Римана, это повышает вероятность, что она истинна. Но это спорный вопрос. Ведь дзета-функция дает бесконечно много нулей, и может статься, что они покажут свое истинное лицо лишь на невообразимо дальних далях дзета-ландшафта – в краях, которые, вероятно, исследуют лишь значительно позднее миллионного года. Те, кто слепо признают истинность гипотезы Римана, не должны забывать, что в истории математики прослеживается интересная закономерность: в алгебре утверждения, долго остававшиеся гипотезами (теорема Ферма), как правило, оказываются истинными, а в математическом анализе (подобные гипотезе Римана) часто бывают ложными.

Сегодня большинство математиков, пытающихся расколоть гипотезу Римана, исходят в основном из эстетических соображений: гипотеза Римана проще и красивее, чем ее отрицание, и приводит к самому «естественному» распределению простых чисел. «Если существует много нулей, отклоняющихся от линии, а такое может быть, вся картина становится просто ужасной, ужасной, уродливой», – сказал математик Стив Гонек. Едва ли у этой гипотезы найдутся какие-то практические последствия, но для математиков, которые ее исследуют, это не играет никакой роли. «Я никогда не делал ничего “полезного”, – похвалялся Г. Г. Харди в своей знаменитой книге «Апология математика». – Ни одно мое открытие не способствовало ни прямо, ни косвенно увеличению или уменьшению добра или зла и не оказало ни малейшего влияния на благоустроенность мира». Математики вроде Харди признают за собой два мотива: во-первых, чистое удовольствие, которое приносят занятия математикой. Во-вторых, ощущение, что они будто астрономы, вглядывающиеся в платоновский космос чисел, – космос, который выходит за пределы человеческой культуры и любых других возможных цивилизаций и сейчас, и в будущем. Харди добавляет, что «число 317 простое не потому, что мы думаем так, и не потому, что наш разум устроен так, а не иначе, а потому, что это так, потому, что математическая реальность устроена так». Ален Конн, французский математик, которого очень многие считают главным кандидатом на доказательство гипотезы Римана, тоже ревностный платоник. «Я считаю, – говорил Конн, – что последовательность простых чисел… обладает реальностью значительно более неизменной, чем окружающая нас физическая реальность».

Однако будет ли все это считаться истинным в миллионном году? Мне думается, что когда мы лучше поймем, что такое простые числа, они утратят свою трансцендентную репутацию. И тогда мы увидим, что они, как и вся остальная математика (или, если уж на то пошло, как религия), созданы человеком, что это сугубо земной артефакт. Когда же нам ждать великого развенчания? Пал Эрдеш, самый плодовитый (и непоседливый) из современных математиков, говорят, утверждал: «Прежде чем мы поймем, что такое простые числа, пройдет еще миллион лет, не меньше». Однако принцип Коперника дает совсем другую оценку. Вопрос о дзета-гипотезе Римана был открыт 160 лет назад самим Риманом. Это значит, что можно с уверенностью 95 % утверждать, что он останется неразрешенным еще года четыре (¹/₃₉×160), однако получит ответ в течение ближайших шести тысяч лет (39×160), то есть гораздо раньше миллионного года. Когда и если он будет решен, простые числа наконец лишатся флера космической инаковости.

Простые числа определяют дзета-функцию, дзета-функция задает нулевые точки, нулевые точки совокупно хранят тайну простых чисел. Если удастся доказать или опровергнуть гипотезу Римана, это замкнет этот тесный кружок, превратив «загадку» простых чисел в тавтологию – такую же, как утверждение «четвероногое животное – это животное». Поэтому я предсказываю, что задолго до миллионного года математики пробудятся от своего коллективного платоновского сна. Никому и в голову не придет направлять последовательность простых чисел через весь космос. Наши потомки отмахнутся от них, как герой «Кошмара математика» Бертрана Рассела: «Прочь! Вы всего-навсего Символические Совпадения!»

∞

А что же смех? Как я уже заметил, нет ничего более узкого, местного, эфемерного, чем тот тип «юмора», который заставляет засмеяться. И ничего более низменного. На протяжении почти всей человеческой истории комическое было смесью скабрезности, агрессии и глумления. Что до особого пыхтения и раздувания грудной клетки, которые оно вызывает, это рассматривалось как «избыточный рефлекс», на первый взгляд не имеющий отношения к выживанию наиболее приспособленных.

Однако в последние годы ученые, поднаторевшие в изящном искусстве эволюционной психологии, нашли гораздо более изобретательный подход к поиску дарвинистских обоснований для смеха. Пожалуй, самую правдоподобную гипотезу выдвинул нейрофизиолог В. Рамачандран. В своей книге «Фантомы мозга», написанной в 1998 году в соавторстве с Сандрой Блейксли (Ramachandran, V., Blakeslee, S., Phantoms in the Brain), Рамачандран выдвигает «теорию ложной тревоги». Возникает потенциально опасная ситуация, у тебя запускается реакция «бей-или-беги», оказывается, что тебе просто показалось, и ты оповещаешь свою социальную группу (генетически близкую), что опасность мнимая, издавая стереотипные звуки – которые к тому же распространяются от одного члена группы к другому, поскольку заразительны. Когда эволюция наладила этот механизм, гласит гипотеза, его удалось направить на другие цели – например, на выражение враждебности к другим социальным группам (или утверждение превосходства над ними) и на высвобождение запретных социальных порывов в пределах своей группы. Однако в основе первоначального механизма «ложной тревоги» лежит ощущение несоответствия: страшная опасность оказалась пустяком, грозное «что-то» обернулось безобидным «ничем». А эволюция юмора с течением тысячелетий привела к тому, что роль несоответствия становилась все главнее. Высшее проявление смеха считается сейчас выражением интеллектуальной эмоции. Наверное, вершиной эволюции остроумия можно считать еврейские шутки, талмудически-изысканную игру с языком и логикой (вспомните свои любимые реплики Граучо Маркса или Вуди Аллена). С такой интеллектуальной точки зрения сильнейший стимул для смеха – это чистое абстрактное несоответствие. Как считал Шопенгауэр, хорошая шутка – это неправильный силлогизм. (Например: «Главное – быть искренним. Сможешь это изобразить, и дело в шляпе».) А несоответствие – полная противоположность старой скучной тавтологии. И так же универсально.

Вот почему я считаю, что юмор и математика к миллионному году поменяются местами. Но какими они будут, шутки той далекой эпохи? Высшая разновидность смеха пробуждается, когда мы видим, как несоответствие разрешается каким-то остроумным способом, что приводит к эмоциональной встряске от приятного узнавания. Мы воображаем, будто перед нами что-то непонятное и загадочное – а вдруг оказывается, что перед нами нет вовсе ничего. Именно таким и будет разрешение загадки дзета-гипотезы Римана, когда его наконец найдут в невообразимом будущем. Под раскаты хохота платоническая инаковость простых чисел обернется тривиальной тавтологией. Если задуматься, что гипотеза, которую сегодня считают величайшей задачей, порожденной человеческим разумом, вполне может в миллионном году оказаться грубоватой шуткой, достойной школьника, это очень отрезвляет.