Глава 5
От семи мостов до шести рукопожатий
Формальное изучение сетей началось в середине XVIII века, когда переживал пору расцвета восточнопрусский город Кёнигсберг, родина философа Иммануила Канта. Среди достопримечательностей Кёнигсберга были семь мостов через реку Прегель, соединявших противоположные берега с двумя островками посреди реки, а также сами эти островки между собой (см. илл. 4). Местные жители давно заметили, что невозможно пройти по всем семи мостам, не пройдя по одному из них хотя бы дважды. Эта задача привлекла внимание великого математика Леонарда Эйлера, уроженца Швейцарии, и в 1735 году он разработал теорию графов, чтобы наглядным и научным способом доказать, почему такой маршрут невозможен. На упрощенном графе, или схеме (см. илл. 5), четыре “вершины” обозначают два берега реки и два острова, больший и меньший, а семь “ребер” обозначают соединяющие их мосты. Строго говоря, Эйлер продемонстрировал, что возможность существования пути, который пересекал бы каждое ребро всего один раз, зависит от степени вершин (то есть количества ребер, сходящихся к каждой вершине). Граф должен иметь либо две вершины с нечетным количеством ребер, либо ни одной. Поскольку в графе, изображающем семь кёнигсбергских мостов, четыре таких вершины (одна с пятью ребрами, остальные с тремя), Эйлеров путь в нем невозможен. Пройтись по всем мостам, не пройдя ни по одному из них дважды, можно было бы, только убрав одно ребро – то есть мост между двумя островами: тогда остались бы только две вершины с нечетной степенью. Со времен Эйлера основными единицами теории графов, которую он сам изначально называл “геометрией положения”, являются вершины (узлы) и ребра (звенья).
В XIX веке ученые стали применять этот принцип ко всему – от картографии до электрических цепей и до изомерии органических соединений. О том, что могут существовать еще и общественные сети, тоже, разумеется, задумывались крупные политические мыслители того времени – в частности, Джон Стюарт Милль, Огюст Конт и Алексис де Токвиль. Последний из них обратил внимание на то, что большое количество разного рода общественных объединений на раннем этапе существования США сыграло важную роль в формировании американской демократии. Однако ни один из них не пытался изложить свои догадки в связной форме. Поэтому можно считать, что изучение социальных сетей ведет свой отсчет с 1900 года, когда школьный учитель и обществовед-любитель Иоганн Делитч опубликовал схему, отображавшую характер дружеских отношений между 53 учениками, с которыми он занимался в течение 1880/81 учебного года. Делитч выявил четкую связь между близостью общественного положения мальчиков и их академической успеваемостью (на основе которой в ту пору рассаживали учеников в классе). В чем‐то сходная работа была проделана тремя десятилетиями позже в Нью-Йорке, где психиатр Якоб Леви Морено, своеобразная личность – австриец по рождению, но при этом противник Фрейда, – составлял социограммы, изучая взаимоотношения между девочками, малолетними преступницами, в исправительной школе в Гудзоне, штат Нью-Йорк. В его исследовании, опубликованном в 1933 году под названием “Кто выживет?” (Who Shall Survive?), показывалось, что большой рост числа сбежавших из учреждения в 1932 году становится объяснимым, если знать, какое место занимали беглянки в школьной социальной сети симпатий и антипатий, имеющих как расовый, так и сексуальный характер (см. вкл. № 2). Вот здесь, заявил Морено, и скрыты “общественные силы, которые господствуют над человечеством”. Его книга, считал он, станет “новой настольной книгой – руководством по социальному поведению, по человеческим сообществам”.
Спустя еще тридцать лет лингвист и библиограф Юджин Гарфилд придумал сходный графический способ наглядно показывать историю разных научных областей при помощи “историограммы” цитат. С тех пор индексы цитирования и “факторы влияния” стали стандартными инструментами измерения академических достижений в науке. А еще они дают возможность отображать процесс появления новых научных идей – например обнаруживая “невидимые колледжи”, которые вызываются к жизни сетями цитирования и которые весьма отличаются от тех настоящих колледжей, где работают большинство ученых. Впрочем, подобные показатели иногда говорят лишь о том, что ученые склонны цитировать труды тех ученых, кто близок им по взглядам. Как гласит старая пословица, свой своему поневоле брат. Это относится не только к цитированию, но и ко многому другому. Если два узла связаны с третьим, то высока вероятность, что они окажутся связаны и друг с другом, потому что (говоря словами экономиста Джеймса Э. Рауха) “два человека, которые знакомы со мной, будут знакомы между собой с большей вероятностью, чем два произвольно выбранных человека”. Триада, все участники которой связаны между собой положительными чувствами, называется “уравновешенной” и иллюстрирует изречение “друг моего друга – мой друг”. Другая триада, два участника которой не знают друг друга, хотя знают третьего участника, иногда называется “запретной триадой”. (Вариант, при котором два участника дружны между собой, а третий враждебен одному из них, являет собой пример такой неприятной ситуации, когда “враг моего друга – мой друг”.)
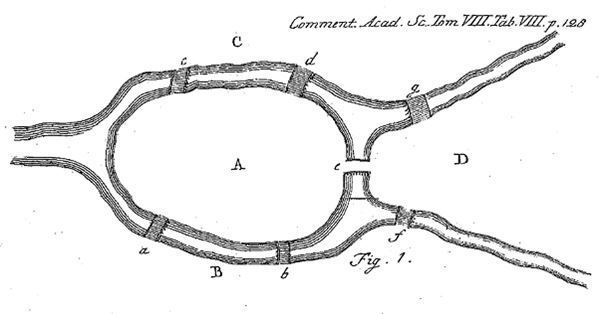
Илл. 4. Иллюстрация № 1 Эйлера из его книги Solutio problematis ad geometriam situs pertinentis [лат. “Решение задачи, связанной с геометрией положения”] (1741). Те, кто пожелал бы испытать решение задачи на месте, уже не имеют возможности сделать это, так как два из семи старинных мостов не пережили бомбежек города во время Второй мировой войны, а еще два были разрушены уже после того, как Кёнигсберг стал советским Калининградом.
Таким образом, гомофилия – наша склонность испытывать притяжение к людям, похожим на нас самих (ее еще называют ассортативностью), – может считаться первым законом работы социальных сетей. Эверетт Роджерс и Дилип Бхоумик первыми из социологов предположили, что гомофилия может оборачиваться и минусами, ограничивая круг общения человека; они высказали мысль, что существует и “оптимальная гетерофилия”. Не выступает ли гомофилия своего рода самосегрегацией? В 1970‐х годах Уэйн Зэкери выстроил схему дружеских связей между членами университетского клуба каратистов. Эта схема выявила наличие двух отчетливо обозначенных групп внутри клуба. Гомофилия может основываться на общем статусе (это и заданные характеристики, например расовая, национальная, половая и возрастная принадлежность, и приобретенные характеристики, например религиозная принадлежность, образование, профессия или модель поведения) или на общих ценностях, поскольку их возможно отличить от приобретенных черт. Знакомая иллюстрация этого явления – наклонность американских школьников самоизолироваться на основе расовой и национальной общности (см. вкл. № 3), хотя недавние исследования и наводят на предположение, что эта тенденция существенно разнится от одной расовой группы к другой.
Могут ли такие схемы показать нам, кто из людей играет главные роли? Лишь в ХХ веке ученые и математики формально определили значимость такого понятия, как “центральность”. Три важнейших показателя важности в формальном сетевом анализе – это центральность по степени, центральность по посредничеству и центральность по близости. Центральность по степени – по количеству ребер, исходящих от одного конкретного узла, – служит показателем общительности: это просто число отношений, которыми один человек связан с другими. Центральность по посредничеству – понятие, официально закрепленное социологом Линтоном Фрименом в конце 1970‐х годов, – позволяет оценить количество информации, проходящей через тот или иной узел. Подобно тому как пассажиры общественного транспорта, стремящиеся побыстрее добраться до места назначения, создают заторы на немногочисленных пересадочных станциях, участники одной общей сети тоже часто обращаются к нескольким ключевым фигурам, которые способны связать их с другими, более отдаленными от них людьми или группами людей. Фигурами, обладающими центральностью по посредничеству, необязательно являются люди, имеющие наибольшее количество связей: важно, чтобы у них имелись по‐настоящему важные связи. (Иными словами, дело не в количестве, а в качестве ваших знакомств.) Наконец, центральность по близости – это показатель, учитывающий среднее количество “шагов”, которые требуется совершить каждому узлу, чтобы добраться до всех остальных узлов; его часто используют, чтобы определить, у кого имеется наилучший доступ к информации – при условии ее широкого распространения. Люди, обладающие высокой центральностью по степени, по посредничеству или по близости, каждый на свой лад служат основными “узлами связи”.
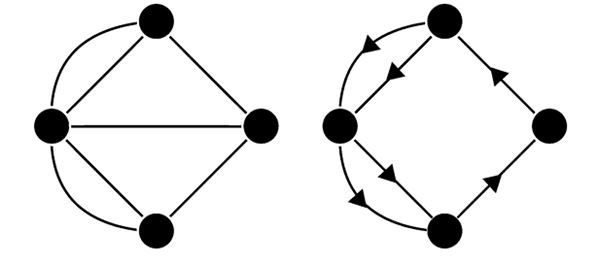
Илл. 5. Упрощенная схема Эйлеровой задачи о кёнигсбергских мостах. Задачу можно решить, только убрав грань в середине (то есть мост, соединяющий два острова, на илл. 4).
В середине ХХ века произошел и существенный прогресс в нашем понимании совокупных свойств сети, которые зачастую остаются незаметными с точки зрения любого отдельного узла. Р. Дункан Люче и Альберт Перри из Массачусетского технологического института предложили использовать коэффициенты “кластеризации” для измерения той степени, в которой связаны между собой узлы в группе, причем крайним случаем считается клика, внутри которой каждый узел связан со всеми остальными в группе. (Строго говоря, коэффициент кластеризации показывает количественное соотношение полносвязанных общественных триад, то есть таких, в которых каждый член любой троицы связан с двумя остальными.) Плотность сети – похожий критерий взаимосвязанности.
Важность таких единиц измерения стала очевидной в 1967 году, когда социальный психолог Стэнли Милгрэм провел свой знаменитый эксперимент. Он направил письма произвольно выбранным адресатам, жившим в Уичито, штат Канзас, и в Омахе, штат Небраска. Получателей просили переслать письмо напрямую намеченному конечному адресату – соответственно, жене одного студента-богослова из Гарварда и одному биржевому маклеру в Бостоне, – если они лично знают этих людей, или же переслать письмо кому‐нибудь, кто, по их мнению, может знать конечного адресата, при условии, что они сами коротко знакомы с посредником. А еще их просили отправить Милгрэму открытку отслеживания и в ней рассказать о том, что именно они сделали. В целом, по сообщению Милгрэма, 44 из 160 писем из Небраски в итоге были доставлены по назначению. (Более позднее исследование наводит на предположение, что таких писем было всего 21.) Законченные цепочки позволили Милгрэму подсчитать количество посредников, задействованных для того, чтобы доставить письмо по назначению: в среднем оно равнялось пяти. Это открытие предвосхитил венгерский писатель Фридьеш Каринти в рассказе “Звенья цепи” (Láncszemek), напечатанном в 1929 году: там главный герой держит с приятелями пари, что сумеет связаться с любым человеком на Земле, кого бы они ни назвали, всего через пятерых общих знакомых, из которых ему самому нужно лично знать всего одного. К этой же задаче подступались и другие исследователи, проводившие эксперименты независимо друг от друга, – в частности, политолог Итиэль де Сола Пул и математик Манфред Кохен.
Сеть, в которой два узла связаны через пятерых посредников, имеет шесть ребер (звеньев). Выражение “шесть рукопожатий” [буквально – шесть степеней разделения] прижилось лишь после появления в 1990 году одноименной пьесы Джона Гуэра, но у него имелась долгая предыстория. Как и представление о том, что “мир тесен” (так назвали диснейлендовский аттракцион, придуманный в 1964 году), или техническое понятие близости, эта фраза очень емко подытоживает ощущение взаимосвязанности, усилившееся в середине ХХ века. Эта тема разыгрывалась во множестве вариаций: шесть шагов до Марлона Брандо, шесть шагов до Моники Левински, шесть шагов до Кевина Бейкона (этот вариант даже превратился в настольную игру), шесть шагов до Луизы Вайсберг (матери одного из друзей Малкольма Гладуэлла), а еще – если обратиться к научным аналогам этих игр – шесть шагов до математика Пала Эрдёша, который, как известно, заложил основы теории сетей. Недавно проведенные исследования позволяют предположить, что количество этих рукопожатий сейчас скорее ближе к пяти, чем к шести, а это, в свою очередь, наводит на мысль о том, что с 1970‐х годов технический прогресс, пожалуй, принес не такие уж разительные перемены в нашу жизнь, как принято считать. Впрочем, для директоров тысячи самых крупных компаний, по версии журнала Fortune, это число составляет 4,6. А для пользователей сети Facebook оно составляло 3,74 в 2012 году и только 3,57 – в 2016‐м.

