4. Контактные силы
Теперь, когда мы объяснили природу электростатической силы, мы сможем представить различные контактные силы, существующие на нашем уровне, которые из нее проистекают.
Они включают контакт с воздухом или водой, что позволит нам ввести понятие давления и объяснить природу силы Архимеда. Это поможет нам понять, почему на высоте давление понижается, как летают воздушные шары и как плавают некоторые предметы.
Электростатическая сила покажется нам далекой. И действительно, в каждом кубе материи со стороной 1 мм заключено примерно сто миллиардов миллиардов атомов, то есть невозможно рассмотреть действие электростатической силы для каждого из них в отдельности, чтобы вывести результат для нашего масштаба. Так что придется обойтись эмпирическими законами, выведенными с помощью опытов. Эти законы не являются фундаментальными, ибо они лишь следствие электростатической силы.
1. Взаимодействие твердых тел
Влияние шероховатости
Сила реакции опоры
Когда мы стоим прямо и неподвижно, на нас действует сила почвы. Согласно формуле ma→; = F→; наш вес должен сообщать нам ускорение, направленное вниз: если этого не происходит, значит, сопротивление почвы полностью компенсирует наш вес.
Не существует никакого специального выражения, описывающего силу, не дающую нам провалиться сквозь землю: каждый раз эта сила такой мощности, чтобы объект не мог пройти сквозь опору (мы рассматривали причину этого на атомном уровне).
Таким образом, чем больше вес предмета, поставленного на поверхность, тем больше сила, с которой поверхность действует на тело, чтобы свести ускорение к нулю.
Если предмет ни в коем случае не может иметь перпендикулярного ускорения на плоской поверхности, зато он может иметь ускорение, направленное вдоль поверхности. Например, если мы положим кусок льда на наклонную поверхность (➙ рис. 4.1 а): часть его веса побуждает его пройти сквозь поверхность, но эта часть встречает противодействие поверхности. Другая часть веса влечет лед вниз по склону, эту часть ничто не уравновешивает, и лед скользит вниз. Теперь заменим лед на что-нибудь более шершавое, например на резину (➙ рис. 4.1 b): при условии, что склон будет не слишком крутым, мы убедимся, что резина останется на месте. Это означает, что на этот раз «что-то» оказывает некое дополнительное воздействие, которое мешает весу заставить тело пройти сквозь опору. Чтобы таким образом нейтрализовать действие веса, эта новая сила направлена вдоль склона и вверх.
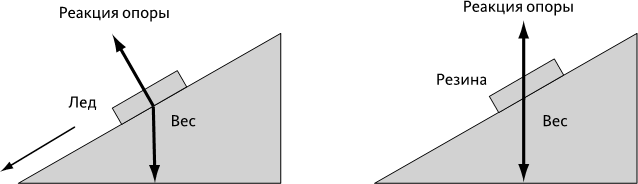
Рис. 4.1 – Силы, действующие на лед и резину на наклонной поверхности
(b) – действие веса и реакция опоры вместе составляют силу, толкающую лед вниз по склону. (b) – в реакции опоры одна из составляющих сил, благодаря контакту с шершавой поверхностью, направлена вверх, что сводит общую силу к нулю.
В итоге мы можем разделить реакцию опоры на две составляющих:
• «нормальная» составляющая (перпендикулярная поверхности), которая не дает объекту пройти сквозь опору;
• тангенциальная составляющая (действующая вдоль поверхности), препятствующая скольжению объекта вдоль поверхности (➙ рис. 4.2).
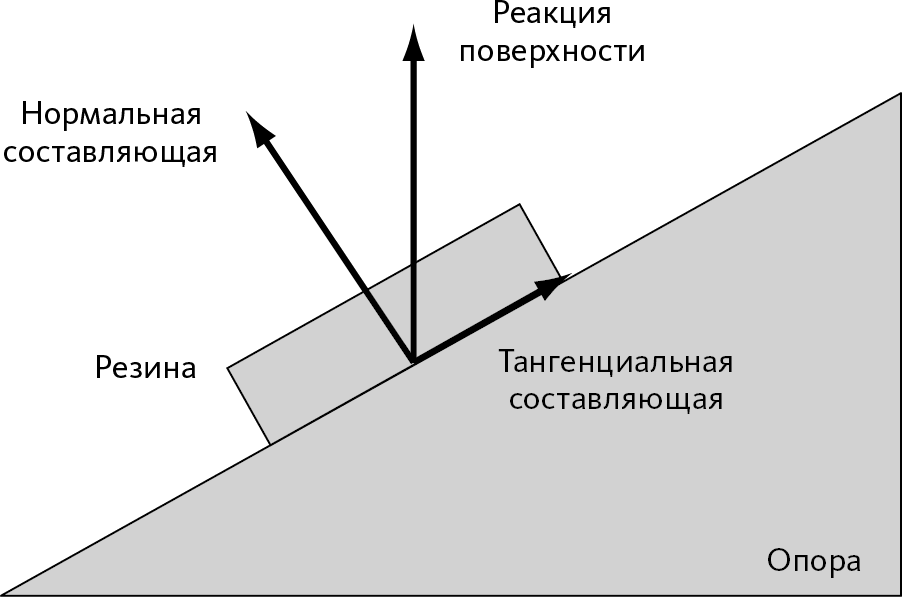
Рис. 4.2 – Составляющие реакции опоры
Микроскопические аспекты контакта
Как поверхность может проявлять тангенциальную силу? Чтобы точно понять, что происходит, нужно ближе присмотреться к месту соприкосновения резины и поверхности, на микроскопическом уровне (этот уровень будет промежуточным между размером атома и резины).
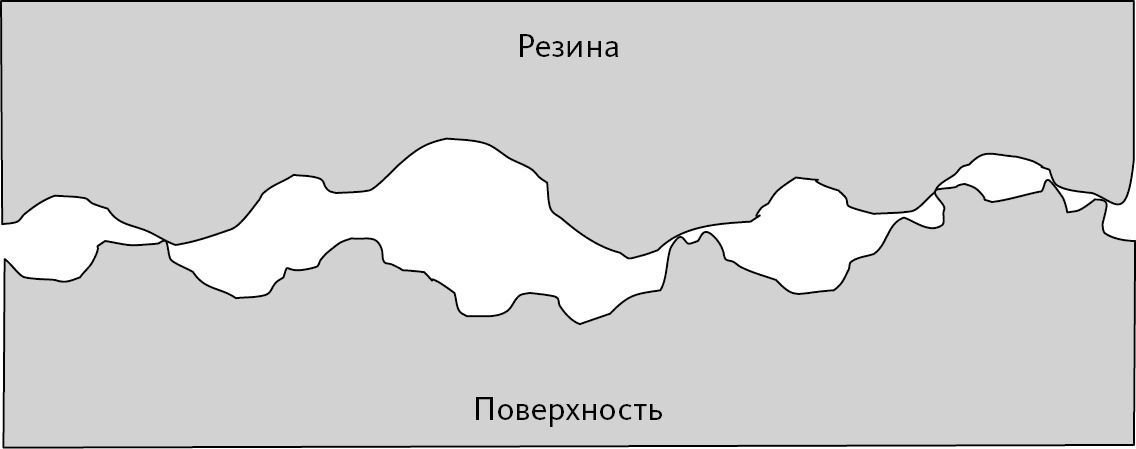
Рис. 4.3 – Соприкосновения двух твердых тел: вид под микроскопом
На рис. 4.3 показано, что мы рассматриваем в данном случае: поверхность соприкосновения двух твердых тел, которая при взгляде невооруженным глазом кажется гладкой, но на деле вся состоит из бугорков. Даже хорошо отполированная поверхность на микроскопическом уровне представляет собой ту же картину.
Мы убедились в следующем:
• Прежде всего, контакт происходит на уровне маленьких бугорков двух твердых тел, а вовсе не вдоль поверхности. То есть, несмотря на видимость, два твердых тела прикасаются друг к другу лишь частично, а большую часть так называемой «контактной зоны» занимает воздух.
• Затем мы видим, что «бугорки» в какой-то степени цепляются друг за друга, что не дает двум поверхностям скользить друг по другу. Именно это объясняет неподвижность резинки даже на наклонной поверхности: таким образом, мы видим, что сила, с которой поверхность действует на предмет, проявляется не только перпендикулярно, но и вдоль.
Трение твердых тел
Продолжим наш опыт и положим резину на плоскую поверхность, которую будем постепенно наклонять: мы убедимся, что при определенном угле наклона резина поедет вниз. Это значит, что существует предел, за которым соприкосновение с шершавым предметом перестает уравновешивать силу, придающую ускорение, в данном случае вес. Тангенциальная реакция опоры проявляется здесь в виде трения: она препятствует скольжению предмета и тормозит его.
Проведем пару небольших опытов, чтобы определить силу этого трения твердых тел. Возьмите какой-нибудь предмет (например, эту книгу) и заставьте ее скользить по поверхности, просто подталкивая ее: если все идет нормально, это будет нетрудно…
Теперь проделайте то же самое, сильно надавив на предмет, который вы заставляете скользить: тем самым вы увеличиваете нормальную реакцию поверхности, которая не дает предмету пройти сквозь нее. Теперь вы чувствуете, что двигать предмет стало намного труднее.
Если точнее, сила трения твердых тел прямо пропорциональна силе нормальной реакции опоры (➙ рис. 4.4).
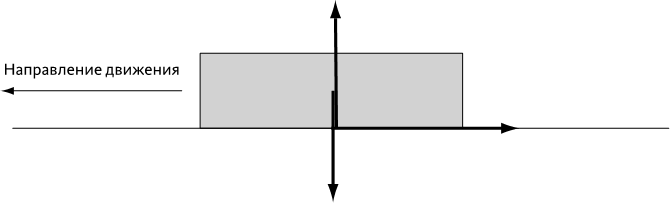
Рис. 4.4 – Силы, приложенные к предмету, двигающемуся по поверхности
В данном примере нормальная реакция (N→;) компенсирует вес (P→;). Тангенциальная составляющая (F→;) соответствует трению твердых тел. Т пропорционально N.
Эта формула была выведена Шарлем де Кулоном, который дал свое имя этому закону. Если FTP – сила трения твердых тел, а N – сила нормальной реакции опоры, мы получаем выражение FTP = μ ⋅ N, где μ – коэффициент трения, который зависит от рода вещества (чем более шершавая поверхность, как у резины, тем больше сила трения FTP).
ВЕСЬМА ПОЛЕЗНАЯ ШЕРОХОВАТОСТЬ
Трение твердых тел может показаться большим неудобством, препятствующим движению; на самом же деле микроскопические неровности, лежащие в основе трения, абсолютно необходимы для движения по любой поверхности. Если бы наши ноги не «цеплялись» за землю на микроскопическом уровне, ходить было бы невозможно: наши ноги скользили бы как на льду, и мы не могли бы продвинуться вперед ни на шаг.
Если точнее: когда резина стремится поехать вниз по склону, сила трения действует в обратном направлении, чтобы ее остановить. И наоборот, когда мы ставим ногу на землю, а потом пытаемся сдвинуть ее назад, сила трения направлена вперед, чтобы не дать ноге сдвинуться: речь идет о нашей силе тяги, единственной, которой мы располагаем.
Та же картина наблюдается со всеми видами наземного транспорта: машинами, поездами… Колесо, крутящееся на гладком льду, останется на месте, ибо не возникает никакой силы, направленной вдоль поверхности (см. схему ниже). Зато шершавая поверхность создает тангенциальную силу, препятствующую скольжению: колесо больше не скользит по поверхности. С другой стороны, тангенциальная реакция толкает колесо вперед: колесо вертится, не скользя.
Отсюда вывод: шероховатость поверхности не только не препятствует поступательному движению транспортного средства (нет движения, значит, нет и силы трения), но именно она и является движущей силой, перемещающей машину. Какой переворот произвело изобретение колеса!
Для движения колеса необходимы хорошие шероховатые материалы: дорожное покрытие и резиновые шины. Лучшие шины те, которые имеют наилучшее сцепление с дорогой.
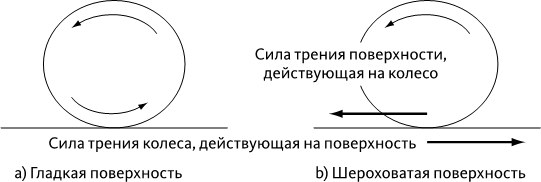
(а) – из-за гладкости поверхности на колесо не действует сила трения: колесо стоит на месте. (b) – благодаря шероховатости поверхности тангенциальная реакция опоры выступает движущей силой: именно она заставляет машину двигаться.
Вернемся к опыту с куском резины на наклонной поверхности. При определенном угле наклона резина начинает скользить вниз. Возьмем брусок из такой же резины, но более тяжелый и крупный: брусок начинает съъезжать при том же угле наклона.
Здесь уравновешиваются две силы:
• больший вес более крупного бруска сильнее толкает его вниз;
• больший вес более крупного бруска вызывает более сильную реакцию наклонной опоры а следовательно, и более сильное трение.
Простое математическое выражение показывает, что две силы компенсируют друг друга. Иными словами: угол начала движения зависит только от материала соприкасающихся поверхностей – и это отличный способ измерить коэффициент трения различных материалов.
Пружинящая сила!
Подвесим лампочку на нитку: лампочка висит неподвижно, что означает, что сила натяжения нити компенсирует вес лампочки. По примеру реакции опоры сила натяжения нити всегда адаптируется к величине веса подвешенного предмета.
Теперь заменим нить на пружину: если к ней не подвешен предмет, пружина имеет «естественную» длину, которую физики называют длиной без нагрузки. Если мы подвесим на пружину лампочку, пружина растянется на некоторую длину. Если мы подвесим на нее предмет вдвое тяжелее, мы увидим, что растяжение пружины увеличилось вдвое (➙ рис. 4.5). Это значит, что растяжение пружины пропорционально приложенной к ней силе.
Если мы обозначим приложенную силу F, а х – растяжение пружины по отношению к длине без нагрузки, получается, что F = kx.
k называется коэффициентом упругости пружины: чем она больше, тем пружина жестче, то есть растягивается или сжимается с трудом.
F соответствует силе, с которой предмет действует на пружину: то есть это также и сила действия пружины на предмет (принцип взаимодействия). Эта сила стремится вернуть пружину к длине без нагрузки: это называется силой упругости пружины.
Выражение F = kx важно, потому что оно означает, что пружину с определенным коэффициентом упругости можно использовать для измерения сил, – здесь попросту используется измерение длины. Пружина, измеряющая силу, называется «динамометр». Мы уже использовали его для измерения гравитационной и электростатической силы в предыдущих разделах (➙ рис. 2.2 и 3.1).
Кроме того, пружины служат амортизаторами в транспортных средствах. Отметим также, что многие физические явления (в частности, на атомном уровне) происходят благодаря силам, действующим по типу пружины, которые не стоит недооценивать.
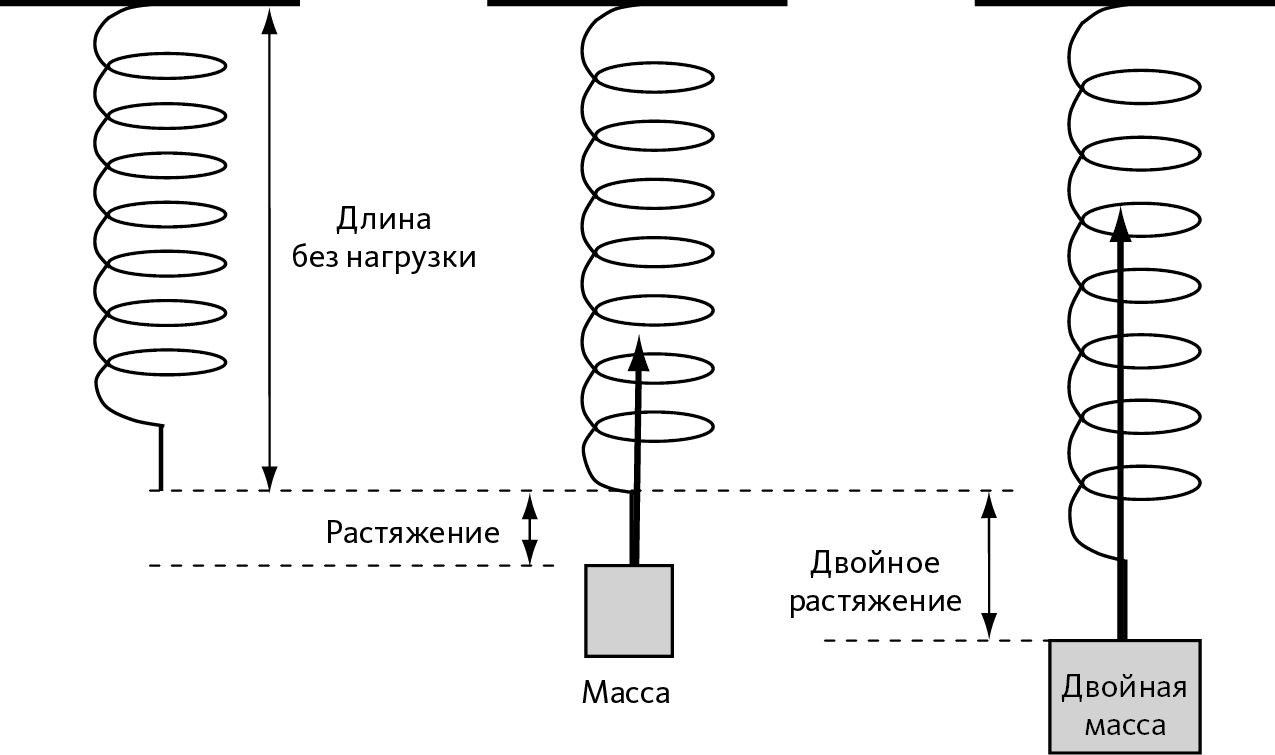
Рис. 4.5 – Сила упругости пружины


