12.1. Палитра методов расчета мультипликаторов

Дамодаран в своем классическом учебнике «Инвестиционная оценка» говорит о существовании трех методов расчета мультипликаторов. Согласно его терминологии, это оценка: 1) по сравнимым компаниям; 2) на основе регрессии; 3) исходя из фундаментальных характеристик оцениваемой компании. Представляется, что читателю было бы понятнее, если бы было сказано, что мультипликаторы можно рассчитать либо по аналогии, либо исходя из фундаментальных характеристик оцениваемой компании. В то же время при расчете по аналогии можно либо пользоваться простыми арифметическими средними или средневзвешенными оценками, либо делать расчеты на основе регрессионных уравнений.

В свете рассуждений о значении «схожести» оцениваемой компании и компаний-аналогов возникает вопрос о том, сколько аналогов лучше иметь для корректной оценки. Понятно, что чем их больше, тем большей статистической достоверностью обладают оценки средних величин. С другой стороны, чтобы расширить группу аналогов, в нее придется включать также компании, имеющие меньшее сходство с оцениваемой. Авторы вышеупомянутой книги «Оценивая бизнес. Анализ и оценка закрытых компаний» [Pratt, Nikulita 2010] считают, что одного-двух аналогов недостаточно для серьезных умозаключений, и в этом я с ними полностью согласна. В то же время 10 и более аналогов представляется им большим числом, и они рекомендуют использовать 4–7 сравнимых компаний (естественно, при условии их наличия). В моей практике встречались случаи, когда группа аналогов была существенно шире и сужать ее до 4–7 компаний не имело смысла. Представляется, что число 4–7 могло возникнуть из-за ориентации на один географический рынок. Многие российские компании приходится сравнивать с их «собратьями» на формирующихся рынках различных стран, в том числе стран Азии, Латинской Америки и Восточной Европы, и число аналогов может измеряться даже двузначным числом. По мнению Дамодарана, применение регрессионных уравнений позволяет использовать в качестве аналогов компании из более удаленных отраслевых сегментов, т.е. можно увеличивать выборку аналогов, когда в ней недостаточно аналогов близких. Если же используются какие-либо средние значения, то отклонения от отраслевого принципа чреваты последствиями.

12.2. Методы расчета среднего значения мультипликатора

В этой книге я не буду подробно останавливаться на методах расчета среднего значения мультипликатора для группы аналогов, поскольку здесь мы внедряемся уже в область статистики, где начинают действовать правила получения достоверных оценок. С одной стороны, для расчета достоверного среднего значения желательно, чтобы группа аналогов была достаточно большой. Однако, с другой стороны, всегда нужно помнить, что чем больше группа, тем более отдаленно похожие на оцениваемую компанию аналоги мы в нее включаем, что ведет к искажению результата и т.д. Выбирать нужно золотую середину, универсальное правило на этот счет сформулировать невозможно. Именно в грамотном выборе группы аналогов и проявляются мастерство и опыт аналитика. Если размер группы позволяет, то желательно удалить из выборки крайние значения — самое высокое и самое низкое.

Затем можно вычислить искомый мультипликатор одним из трех способов:

• как среднеарифметическое;
• как средневзвешенное (при этом взвешивать нужно по знаменателю мультипликатора, т.е. P/E взвешивается по чистой прибыли, а P/S — по продажам);
• как медиану мультипликаторов для группы аналогов.

Среди аналитиков нет единодушия в определении, какой из трех способов предпочтителен. На наш взгляд, расчет по среднеарифметическому — самый худший вариант из трех.

Во-первых, нужно помнить, что в случае использования среднеарифметического значения возникает «оптический обман» корректного взвешивания различных мультипликаторов. Казалось бы, данный метод придает одинаковые веса разным мультипликаторам, но на самом деле эти веса разные.

Проиллюстрируем это на примере. Допустим, мы оцениваем компанию по мультипликатору Р/Е. У нас есть два аналога, Р/Е первого аналога равен 15, а второго — 5, тогда среднее значение Р/Е равно 10. Положим, мы хотим инвестировать $200. Как нам нужно их вложить, чтобы получить Р/Е, равный 10? Оказывается, нужно вложить $150 в первую компанию и $50 — во вторую. Тогда мы сможем «купить» $10 чистой прибыли первой компании и $10 чистой прибыли второй, что в сумме даст $20 чистой прибыли, или Р/Е, равный 10 (при вложении $200).

Во-вторых, среднеарифметические значения бывают завышены, особенно это касается мультипликатора Р/Е. Как говорилось выше, недостаток показателя Р/Е состоит в том, что он чаще других бывает отрицательным — в тех случаях, когда компания имеет отрицательную прибыль. Поскольку отрицательные значения мультипликатора смысла не имеют, на практике Р/Е рассчитывается только для выборки прибыльных компаний, что и приводит к его завышению. Между тем в расчет можно включить и убыточные компании. Тогда все компании выборки нужно представить как одну большую компанию, т.е. сначала сложить цены их акций, а затем величины их чистой прибыли на одну акцию и поделить одно на другое. Это и будет взвешиванием в случае с отрицательными значениями знаменателя. Что касается выбора между средним значением или медианой, то медиана считается более точной оценкой, поскольку крайние значения влияют на нее меньше, чем на среднеарифметическое. Особенно это актуально в случае с Р/Е, который может быть равен сколь угодно большому числу для тех компаний, чья прибыль не сильно отличается от нуля. Выход из этой ситуации — отбросить крайние значения при расчете среднего.

12.3. Регрессионное уравнение

Вторым способом расчета требуемого мультипликатора является регрессионное уравнение. Напомним, что регрессия — это линейное уравнение, в котором правая часть объясняет изменение левой части. Например, если я напишу уравнение 5L = 0,55R, где R — выручка компании, а L — затраты на персонал, то его можно будет интерпретировать следующим образом: рост выручки на 1% требует увеличения расходов на персонал на 0,5%. Искусство составления регрессионных уравнений состоит в том, чтобы правильно определить, от каких параметров зависит движение той или иной переменной, и представить в правой части уравнения такой набор независимых параметров, который в максимальной степени объяснял бы изменения переменной в левой части.

Для оценки с использованием мультипликаторов, которые были получены первым путем (как среднее или медиана), нужно внимательно следить за тем, чтобы оцениваемая компания и ее аналог как можно более точно совпадали по рисковости, темпам роста и некоторым другим параметрам. Эмпирическим путем было установлено, что значение показателя Р/S хорошо коррелирует с доходностью продаж или маржей чистой прибыли (регрессионное уравнение вида Р/S = α + β(E/S)), а значение Р/BV — с доходностью акционерного капитала (регрессионное уравнение вида Р/BV = α + βROE).

На самом деле результат в каком-то смысле тривиален. Ведь оба уравнения, по сути, иллюстрируют тот факт, что в конечном счете для оценки компании важна ее доходность. Поэтому оценка компании зависит от того, какую прибыль генерирует $1 продаж и какую доходность на вложенный капитал генерирует $1 активов. Так что данные формулы — еще одно напоминание о том, что оцениваемая компания и ее аналоги в идеале должны быть схожи как по показателям доходности продаж, так и по показателям доходности активов. Регрессия — хороший способ, позволяющий решить эту проб­лему. Ведь регрессия выявляет формулу зависимости величины мультипликатора от этих параметров, следовательно, в выборке аналогов не обязательно должны быть компании, похожие друг на друга, как оловянные солдатики. Таким образом, регрессия применима там, где недостаточно прямых аналогов для расчета мультипликатора.

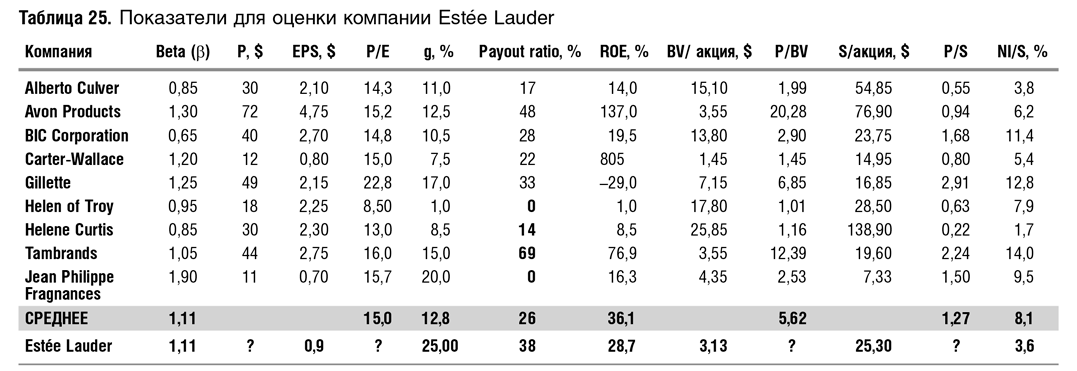
Ниже мы рассмотрим учебный пример расчета мультипликаторов на основе регрессий, заимствованный у Дамодарана. Пример довольно старый, и поэтому он условный, сейчас, конечно, все данные поменялись. В этом примере требуется оценить закрытую компанию Estée Lauder, известного производителя элитной косметики и парфюмерии, на основе оценки рынком публичных компаний схожего профиля. В табл. 25 приводятся данные для Estée Lauder и группы аналогов, состоящей из 9 компаний. Как видно из таблицы, у Estée Lauder ожидаемые темпы роста примерно в два раза выше, чем в среднем для группы аналогов (25 и 12,8% соответственно), доля дивидендов в чистой прибыли несколько выше, доход на акционерный капитал — ниже, а маржа чистой прибыли (Е/S) существенно ниже (3,6% против 8,1%).

Для оценки были выбраны показатели P/E, P/BV и P/S. При этом рассчитывались регрессионные уравнения следу­ющего вида:

• мультипликатор Р/Е регрессировался относительно темпов роста (g), доли дивидендов в чистой прибыли (1 – b) и рисковости ценной бумаги (Р). Полученное в итоге уравнение связывает Р/Е только с темпами роста (g), а это означает, что зависимости от двух других параметров в данном случае не было выявлено;
• мультипликатор Р/BV регрессировался относительно доходности на акционерный капитал (ROE);
• мультипликатор Р/S — относительно маржи чистой прибыли при продажах (E/S), однако в этом случае разница в темпах роста не учитывалась.

В табл. 26 приводятся формулы полученных регрессий и результаты оценки.

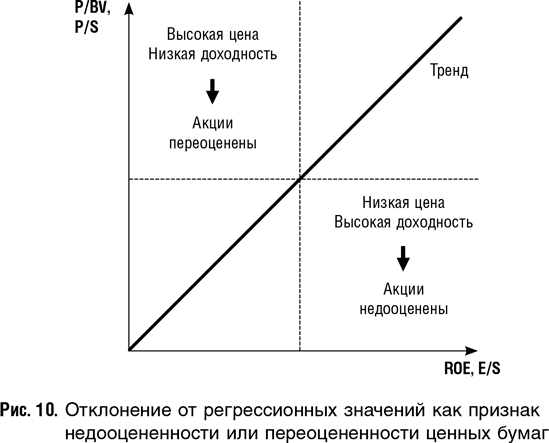
Регрессионное уравнение задает рамки для анализа пере- и недооцененности конкретной ценной бумаги. Результаты регрессионного анализа можно наглядно представить в виде графика (рис. 10). Допустим, по вертикальной оси заданы показатели Р/S или Р/BV, а по горизонтальной — ROE и E/S соответственно. Зависимости между Р/S и E/S, а также между Р/BV и ROE, полученные в результате расчета регрессионных уравнений, представляют собой прямые с положительным наклоном (на нашем рисунке такая прямая обозначена словом «тренд»). Область вокруг прямой можно условно поделить на четыре квадрата. Очень условно можно принять, что при прочих равных удаление конкретной ценной бумаги от тренда «вверх и влево» (высокая цена при низкой доходности) может свидетельствовать о переоцененности этой бумаги, а «вниз и вправо» (низкая цена при высокой доходности) — о недооцененности по сравнению с группой аналогов. Столь схематичное представление, конечно же, следует воспринимать не как догму, а как возможный инструмент, помогающий исследовать проблему недо- и переоцененности акций.

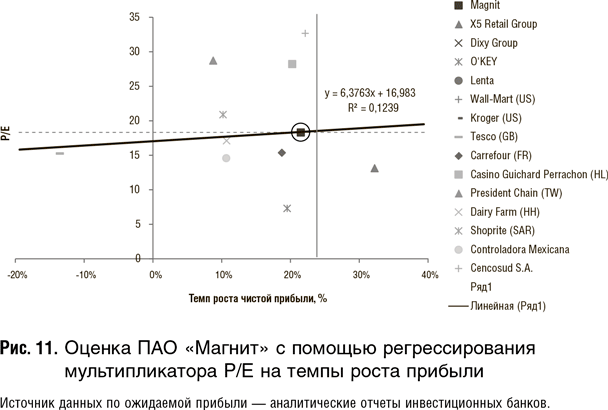
Разберем конкретный пример с подобным вариантом анализа. Посмотрим на оценку российской розничной сети «Магнит» на 10.03.16 с помощью регрессионного уравнения. Регрессировать будем ожидаемые темпы роста чистой прибыли на показатель P/E. На рис. 11 отдельные наблюдения и тренд, в легенде справа — список аналогов. Что здесь можно сказать? Данный анализ не выявляется ни недооценки, не переоценки по сравнению с аналогами: оценка «Магнита» строго на линии тренда. Смущает, однако, то, что линия тренда не является четко выраженной, и значение R2 регрессионного уравнения всего 12%, что немного. (Нечеткий тренд и низкий R2, конечно, связанные вещи.) Но все же вывод о том, что акции «Магнита» не являются недооцененными, я бы сделала. Рекомендации «покупать» не вырисовывается.

Оценка на основе фундаментального анализа редко применима на практике. Связано это с тем, что она является неким «кентавром», у которого передняя половина туловища — дисконтированный денежный поток, а задняя — оценка по аналогии. Для оценки на основе фундаментального анализа, как и для оценки по дисконтированному денежному потоку, требуется найти норму дисконта, которая не нужна для оценки по аналогу. Однако эта оценка менее точна, чем оценка по дисконтированным денежным потокам, и в этом смысле она похожа на оценку по аналогии. По нашему мнению, еще одна промежуточная оценка — между оценками по аналогии и по дисконтированным денежным потокам — практически не добавляет ничего нового к пониманию стои­мости компании или ее ценных бумаг, поэтому на практике ее можно применять не так часто.

12.4. Отраслевая применимость методов

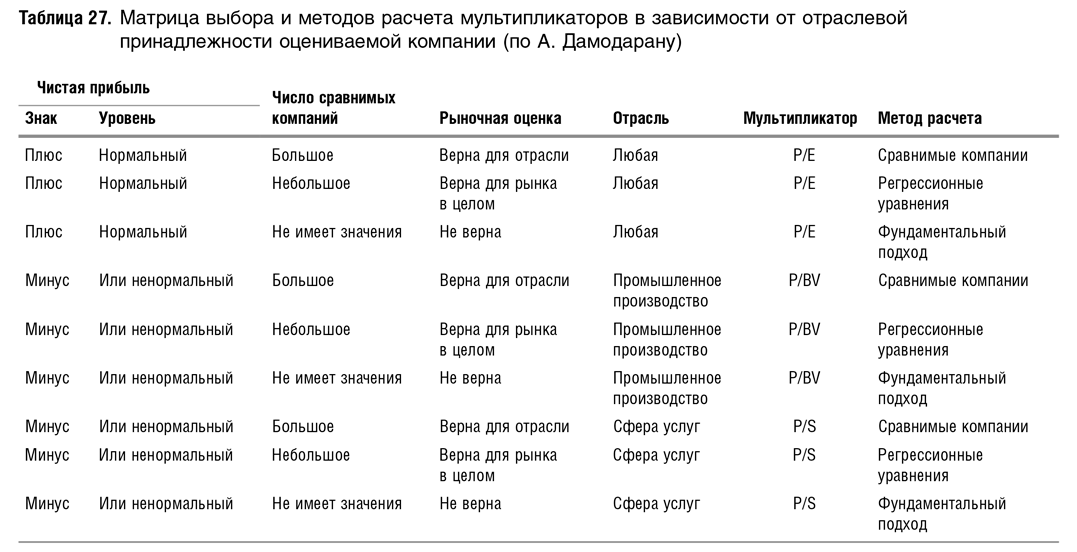
Дамодаран приводит сводную таблицу (табл. 27), по которой можно выбрать, какой из основных показателей лучше использовать и как его рассчитывать. Мультипликатор P/E, например, рекомендуется использовать только для компаний с положительной прибылью, находящейся в диапазоне нормальных (для данной компании) значений. В противном случае искажения будут слишком велики. Оценку по активам предпочтительнее использовать для промышленных компаний, а по продажам — для компаний сферы услуг. Подразумевается, что в промышленности важнее капитальные активы, а в сфере услуг — клиентская база. В тех случаях, когда сравнимых компаний мало или их нет вовсе, предлагается использовать фундаментальный анализ, а когда они есть — регрессионные уравнения или средние оценки.

Дамодаран считает, что в случае небольшого количества сравнимых компаний более применима регрессия. Насколько я понимаю, обусловлено это не тем, что в случае малого количества аналогов она дает более точный результат. Дамодаран считает допустимым в случае регрессии расширить выборку сравнимых компаний за счет более удаленных по своим характеристикам от аналога. Связано это с тем, что если при включении в выборку непохожих компаний среднее может существенно отклоняться от среднего близкого аналога, то при регрессионном уравнении мы имеем дело с формулой зависимости мультипликатора от иных параметров, следовательно, попадание удаленных компаний не должно сильно исказить результат.

В целом я согласна с такой градацией и рекомендую начинающему аналитику ею пользоваться. Более опытный специа­лист всегда будет исходить из конкретной ситуации. Например, в телекоммуникационной отрасли капитальные активы стоят очень дорого, и оценка по активам заслуживает не меньшего внимания, чем оценка по выручке и т.п.

Помимо применимости тех или иных показателей в конкретных отраслях важно еще учитывать такой важный фактор, как разброс значений показателя для группы аналогов. Разброс значений, как правило, измеряется стандартной статистической мерой, например стандартным отклонением. Оно определяется как среднее отклонение от среднего значения, деленное на это среднее значение. Правило таково: чем выше разброс значений того или иного мультипликатора у аналога, тем менее корректно применение этого мультипликатора. Понятно, что для финальной оценки может использоваться несколько мульти­пликаторов, при этом оценке по каждому из них придается определенный вес: например, 30% — оценке по Р/Е, 30% — оценке по Р/S и 40% — оценке по Р/BV. В данном контексте меньший вес придается мультипликатору с большим разбросом, а больший — мультипликатору с меньшим разбросом. На интуитивном уровне это понятно. Меньший разброс значений мультипликатора свидетельствует о том, что он лучше коррелирует со стоимостью.

12.5. Краткие выводы

• Согласно Дамодарану, существуют три метода расчета мультипликаторов: на основе сравнимых компаний, регрессионных уравнений и фундаментальных показателей самой компании. На наш взгляд, методы оценки на основе сравнимых компаний и регрессии — это, по сути, две разновидности оценки по аналогии.
• Фундаментальный анализ используется, когда компаний-аналогов нет или их совсем мало.
• Среднее значение мультипликатора может быть рассчитано как среднеарифметическое, средневзвешенное и медианное значения для компаний выборки. Метод простого среднего — самый уязвимый, так как он придает некорректные веса разным мультипликаторам и часто дает завышенные оценки, особенно в случае с P/E, что объясняется исключением из выборки компаний с отрицательными значениями показателя.
• Регрессионное уравнение решает проблему отсутствия или нехватки прямых аналогов, так как в силу выявления зависимости между ценой компании и факторами стоимости оно позволяет оперировать выборкой компаний из разных отраслей.
• Регрессионный анализ является инструментом для анализа недооцененности и переоцененности акций.
• Для получения финальной оценки по мультипликаторам можно использовать средневзвешенную оценку по разным показателям, при этом бóльший вес желательно давать тому мультипликатору, разброс значений которого для выборки аналогов меньше.