Дайсон
Осенью в Корнеллский университет прибыл Фримен Дайсон. Некоторым математикам из Корнелла были знакомы работы некоего британца Дайсона, но это имя едва ли могло считаться известным. В математике много вундеркиндов, однако никто не верил, что этот невысокий двадцатитрехлетний парнишка с ястребиным носом — тот самый Фримен Дайсон. И все же кое-кто из аспирантов считал его гением и загадкой. Он спал допоздна, приходил в кабинет с газетой, читал ее до обеда, а потом дремал весь день, закинув ноги на стол и прикрыв глаза. Изредка он заходил в кабинет Бете. Что они там делали, никто не знал.
Дайсон действительно был тогда одним из двух или трех талантливейших молодых математиков Англии. Сын высокообразованных англичан из среднего класса, он родился, когда его родители уже достигли среднего возраста (они не спешили вступать в брак). Его отец Джордж был композитором, дирижером и учителем музыки в колледже для мальчиков на юге Англии. Впоследствии он стал директором Королевского музыкального колледжа. Мать Дайсона Милдред выучилась на адвоката, но оставила практику. От нее Фримен унаследовал глубокую любовь к литературе, начиная с Чосера и поэтов Древней Греции и Рима. В шестилетнем возрасте он сидел, обложившись раскрытыми томами энциклопедии и погрузившись в вычисления, которыми было исписано множество листов. Уже тогда он полностью погружался в себя. Однажды старшая сестра прервала его занятия, спросив, куда подевалась их няня. Фримен ответил: «Полагаю, она где-то там, но определенно не здесь». Он прочитал популярную книгу по астрономии «Красота небес», научно-фантастические романы Жюля Верна, а в восемь или девять лет написал собственный фантастический роман — «Эролунарная коллизия сэра Филипа Робертса». Произведение отличалось зрелым ритмичным синтаксисом и по-взрослому непринужденной литературной манерой. Главный герой обладал способностями к арифметике и строил космические корабли. Фримен, не признававший коротких предложений, в пространных выражениях изобразил ученого, спокойно воспринимающего популярность, но вместе с тем одинокого в своей работе:
«Я, сэр Филип Робертс, и мой друг майор Форбс, — начинался роман, — только что разгадали важнейшую тайну природы: мы выяснили, что Эрос, маленькая планета, столь хорошо известная по причине своей близости к Земле, в последующие 10 лет и 287 дней подойдет к Земле на 3 миллиона миль, в то время как обычно она проходит около нашей планеты раз в 37 лет на расстоянии 13 миллионов миль. Следовательно, существует высокая вероятность того, что Эрос попросту столкнется с Землей. Настоятельно рекомендую тщательно просчитать эту вероятность!»
Когда страсти немного улеглись и все разошлись по домам, волнение до конца не утихло. Напротив, все принялись просчитывать самые невероятные сценарии; какие-то из них были рациональными, а какие-то нет. Сэр Филип тем временем спокойно писал что-то в своем кабинете, разве что задерживаясь там чуть дольше обыкновенного. Никто не мог сказать, что у него на уме.
Затем Дайсон прочитал популярные книги об Эйнштейне и теории относительности. Вскоре он понял, что хочет знать больше, чем предусмотрено школьной программой, и выписал каталоги научных издательств. Наконец, мать заметила, что интерес сына к математике превращается в одержимость. Ему было пятнадцать лет, и он только что провел рождественские каникулы, методично, с шести утра до десяти вечера, решая семьсот примеров из учебника Пьяджо «Дифференциальные уравнения». В том же году, к своему разочарованию узнав, что классический учебник Виноградова по теории чисел не переведен на английский, он выучил русский и сам перевел этот труд, записав перевод своим аккуратным почерком. Рождественские каникулы близились к концу; мать пригласила его на прогулку и осторожно начала разговор со слов древнеримского драматурга Теренция: «Я человек, и ничто человеческое мне не чуждо». Она пересказала ему «Фауста» Гете, части первую и вторую, указав на то, что Фауст тоже был погружен в книги, жаждал знаний и власти и ради этого пожертвовал возможностью любить. Этот разговор произвел на Дайсона такое впечатление, что много лет спустя, посмотрев «Гражданина Кейна», он заплакал, узнав на экране того Фауста, о котором говорила мать.
Когда началась война, Дайсон поступил в Тринити-колледж Кембриджского университета. Его учителями стали величайшие английские математики: Харди, Литтлвуд и Безикович. В физике в то время господствовал Дирак. Судьбы Дайсона и Фейнмана в войну сложились по-разному. Британская армия не сумела разглядеть талантов Дайсона, и они остались без применения. Юного гения назначили в командный штаб бомбардировщиков Королевских ВВС в Букингемширском лесу, где он проводил статистические исследования; впрочем, полученные результаты игнорировались, если они противоречили официальному мнению властей. Бесполезность этого труда сильно угнетала его. Вместе с другими сотрудниками отдела стратегических исследований он узнал, что вопреки бытующим в командном штабе стереотипам безопасность пилотов истребителей не возрастает по мере накопления ими опыта; что люки для катапультирования слишком узки, и пилоты не могут воспользоваться ими в экстремальной ситуации; что пулеметы замедляют движение самолета и увеличивают численность команды, не повышая шансы выжить в перестрелке с вражеским истребителем; что британская стратегия бомбардировок обречена на провал. Математика раз за разом опровергала правдивость «примеров из жизни», особенно когда эти примеры передавались из уст в уста и становились мифами, имеющими лишь одну цель — привлечь в пилоты молодежь.
Дайсон видел хаотичные следы от взрывов на снимках, сделанных после вылетов, видел, что немцам удается поддерживать работу заводов, в то время как гражданские районы лежат в руинах. Он работал под бомбежками в Гамбурге в 1943 году и Дрездене в 1945-м и чувствовал, что проваливается в нравственный ад. В Лос-Аламосе военная машина добилась впечатляющих результатов, собрав команду независимых ученых. Бюрократический аппарат, с которым пришлось столкнуться Дайсону, погряз в мелкой и крупной лжи, и ученым из командного штаба бомбардировок не удалось ему противостоять.
Это были темные времена, ознаменовавшие внедрение новых технологий, которые объединили науку и механизированное производство. Даровитая на изобретения Англия всегда относилась к новшествам с недоверием. Машины подрывали традиционный образ жизни, заменяя живую рабочую силу бездушным автоматизмом. На стыке веков в клубах черного дыма, окутывавшего английские промышленные города, в жестоких заводских условиях не было ничего романтичного; люди были склонны скорее идеализировать условия жизни крестьян, хотя те были не менее жесткими. В Америке тоже были свои луддиты, но в век радио, телефонов и автомобилей мало кто посчитал бы технологический прогресс пагубным. Американцы проникнутся ненавистью к технологиям лишь к концу XX века, но эта ненависть зародилась еще тогда, в атмосфере торжества 1945-го, и выросла из страха перед атомной бомбой. Среди книг, которые оказали большое влияние на Дайсона, была детская сказка под названием «Волшебный город», написанная в 1910 году Эдит Несбит. Мораль книги заключается в том, что технологии в ней преподносятся как нечто неоднозначное. Мальчик по имени Филип узнает, что в волшебном городе можно получить в свое распоряжение любой механизм, но при одном условии: пользоваться им придется вечно. Поставленный перед выбором — взять лошадь или велосипед, — Филип поступает мудро и выбирает лошадь. Сказка была написана в те времена, когда мало кто отказывался обменять лошадей на велосипеды, автомобили и тракторы. Узнав об атомной бомбе, Дайсон вспомнил «Волшебный город» и подумал о том, что изобретенную новую технологию уже нельзя «разобрести» обратно. Тем не менее в жизни все не так однозначно, поэтому Дайсон в то же время разделял мнение Д. Г. Лоуренса, отмечавшего приятную чистоту и минималистичность объектов, произведенных машинным способом, будь то книги, стулья, бутылки или кованое изголовье кровати. «Мое желание обладать функциональным предметом, отвечающим моим требованиям, наконец удовлетворено… Поэтому я склоняю голову перед машиной и ее изобретателем». Новость о Хиросиме отчасти стала облегчением для Дайсона. Война для него закончилась. Но он не забыл о том, что в результате стратегических бомбардировок погибло вчетверо больше мирных людей, чем при взрыве атомных бомб. Спустя много лет, когда у него родился сын, он разбудил ребенка среди ночи своим криком, проснувшись от нестерпимого кошмара. Ему снилось, что перед ним горит разбившийся самолет. Рядом стояли люди; некоторые бросались в огонь, пытаясь спасти выживших. Во сне Дайсон не мог пошевелиться, оцепенев от ужаса.
Окружающим Фримен порой казался застенчивым и скрытным, но его учителя в Англии вскоре поняли, что юноша просто блестяще владеет собой. В старших классах он занимался теорией натуральных чисел. В частности, работал над разбиением — так в математике называется способ представить число в виде суммы натуральных слагаемых: например, разбиение числа 4 — это 1 + 1 + 1 + 1, 1 + 1 + 2, 1 + 3, 2 + 2 и 4. Число разбиений быстро возрастает — у числа 14 их уже 135, — и скорость этого возрастания легко определить, используя принципы классической теории чисел. Здесь нет ничего сложного. Первые несколько рядов может просчитать даже ребенок. Размышление над этой теорией открывает перед исследователем великолепный мир, сложный и прекрасный, как оригами. Дайсон пошел по стопам индийского математика-вундеркинда начала XX века Шриванасы Рамануджана. На втором курсе Кембриджского университета Дайсон вывел несколько гипотез о разбиениях, доказать которые не смог. Но вместо того чтобы прекратить попытки, обратил неудачу себе во благо: публикация этих наработок стала его вторым научным трудом. «Используя алгебраические тождества, профессор Литтлвуд никогда не утруждается их доказывать, — писал он об одном из своих знаменитых профессоров. — По его мнению, если найдется человек настолько недалекий, что ему потребуются доказательства верности тождества, это можно будет сделать в нескольких строках. Моя цель — опровергнуть данное убеждение». Дайсон пообещал привести любопытные примеры тождеств, доказать которые ему не удалось. Он также заявлял, что «есть случаи еще более туманные — существование тождеств, которые невозможно не просто доказать, но даже привести… Стоит ли говорить, что я призываю читателей предоставить недостающие доказательства, а еще лучше — недостающие тождества». Дайсон никогда не любил скучных математических диспутов.
Однажды ассистент Дирака сказал Дайсону: «Я ухожу из физики в математику; физика слишком запутана, абстрактна, неуловима». На что Дайсон ответил: «Я ухожу из математики в физику по тем же причинам». Математика казалась ему предметом любопытным, но реальный мир был еще любопытнее. А самым подходящим местом для занятий физикой представлялись Соединенные Штаты. Он никогда не слышал о Корнеллском университете, но ему сказали, что из всех физиков мира лучше всего работать с Бете. А Бете находился в Корнелле.
Дайсон отправился в незнакомую страну с настроем первооткрывателя, готовый встретиться лицом к лицу и с флорой, и с фауной, и с потенциально опасными аборигенами. В Америке он впервые сыграл в покер. Узнал, что такое пикник по-американски: к его изумлению, для американцев это означало приготовление стейков на гриле под открытым небом. Ездил на автомобильные прогулки. «Мы были в диких местах», — писал он родителям вскоре после приезда, имея в виду отрезок пригородной трассы между Итакой и Рочестером. Его компаньоном в путешествиях стал физик-теоретик по имени Ричард Фейнман, «первый встреченный мной представитель редкого вида — ученого, родившегося на американской земле».
«Он разработал свою версию квантовой теории, — писал Дайсон. — Этот человек всегда полон новых идей; большинство из них блестящи, но не имеют практического применения, и почти всегда одно озарение вскоре сменяется другим… Когда он врывается в кабинет и начинает рассказывать об очередной гипотезе, сопровождая свою речь невероятными звуковыми эффектами и размахивая руками, жизнь определенно не кажется скучной».
Хотя формально Дайсон был простым аспирантом, его первым заданием стало исследование актуальной проблемы: Бете, только что вернувшийся с Шелтер-Айленда, поручил ему просчитать вариант Лэмбовского сдвига. Сам Бете уже сделал первый шаг к решению теоретической задачи, поставленной экспериментом Лэмба. Возвращаясь в поезде с конференции, он наспех набросал на клочке бумаги предварительные расчеты, которые вскоре заставили десяток его коллег вздохнуть: «Ну почему мы до этого не додумались?». Когда поезд прибыл в Скенектади, он позвонил Фейнману и попросил его проследить, чтобы эти расчеты попали в руки Оппенгеймеру и прочим присутствовавшим на конференции в течение недели. Это были весьма приблизительные вычисления, подобные тем, что они делали в Лос-Аламосе; в них не учитывались релятивистские эффекты и исключались бесконечности. Впоследствии на смену открытию Бете пришли более строгие расчеты в духе тех, что делал Швингер. Тем не менее Бете первым нашел верное число, почти попал в точку, и физики укрепились в убеждении, что в квантовой электродинамике возможны новые точные эксперименты.
Существующая теория объясняла наличие различных энергетических уровней внутри атома и предоставляла физикам действенный инструмент для их вычисления. Разница величин возникала из-за разных комбинаций квантовых чисел, углового момента электрона, вращающегося вокруг ядра, и углового момента электрона, вращающегося вокруг своей оси. Встроенная в уравнение симметрия приводила к точному совпадению пары величин, обозначающих высчитанные таким способом энергетические уровни. Но в лаборатории Уиллиса Лэмба эти величины не совпали, а значит, ученые что-то упустили из виду. Бете предположил, что этим «чем-то» был давний враг физиков-теоретиков, то, чего все боялись, — самодействие электрона.
Эта дополнительная энергия или масса возникала в результате взаимодействия электрона с собственным полем — процесса, напоминающего проглатывание змеей своего хвоста. Данная величина была всего лишь некой досадной помехой, когда теоретически равнялась бесконечности и незначительно проявлялась на практике. Но сейчас, когда она, оставаясь бесконечной в теории, реально обнаруживалась в эксперименте, игнорировать ее было нельзя. Бете все время держал в уме предположение, выдвинутое на Шелтер-Айленде нидерландским физиком Хендриком Крамерсом: «наблюдаемую» массу электрона (ту, которую теоретики считали его фундаментальным свойством) следует считать комбинацией двух других свойств — собственной энергии и «собственной» массы. Странной парочкой были эти массы — собственная и «наблюдаемая», известные также как «голая» и «одетая». Собственную массу нельзя было измерить напрямую, а наблюдаемую невозможно высчитать на основе базовых принципов. Крамерс предложил метод, позволивший теоретикам вывести число из экспериментальных измерений и «выправить» его, совершить «перенормировку». Бете это удалось — грубо, но эффективно. Между тем с изменением массы менялся и заряд — величина, которую также считали абсолютной. Поэтому и ее пришлось подвергнуть перенормировке, то есть запустить процесс изменения условий уравнения, в ходе которого бесконечные величины становятся конечными. Этот процесс похож на рассмотрение крупного объекта через регулируемую линзу; когда мы поворачиваем регулятор, объект уменьшается, но вместе с тем становится понятно, какой эффект регулировка оказывает на другие объекты, в том числе и сам регулятор. Такая работа требовала большой осторожности.
С одной стороны, перенормировку можно охарактеризовать как вычитание бесконечности из бесконечности с тайной надеждой получить что-то иное. С точки зрения логики подобное действие бессмысленно: бесконечность (последовательность целых чисел — 0, 1, 2, 3…) минус бесконечность (последовательность четных целых чисел — 0, 2, 4…) равняется бесконечности (последовательности нечетных целых чисел — 1, 3, 5…). Они одинаковы, в отличие, к примеру, от существенно более обширной бесконечности, включающей натуральные числа. Физики-теоретики в глубине души уповали на то, что стоит им написать «бесконечность минус бесконечность = ноль», природа чудесным образом вмешается и сделает это правдой, хотя бы раз. Оправдание их надежд означало бы, что они сделали важное открытие о мире. Вот только пока было неясно, какое именно.
Бете поручил Дайсону просчитать простой, «игрушечный» вариант Лэмбовского сдвига — для электрона без спина. Таким образом Дайсон смог бы найти быстрое решение актуальной проблемы, а Бете — продолжить свои изыскания. Дайсон видел, что расчеты, опубликованные Бете, были аферой, но аферой гениальной — очень грубое приближение, каким-то образом попавшее в точку. Он все чаще общался с Фейнманом, который постепенно перестал казаться ему представителем экзотического вида. Обедая у Бете, он наблюдал за тем, как дикий американец вскакивает из-за стола, чтобы поиграть с Генри, пятилетним сыном хозяина дома. Фейнман обожал детей своих друзей. Он развлекал их, болтая на тарабарском языке, жонглировал, изображал различные музыкальные инструменты, как человек-оркестр. Мог заворожить их одним простым действием: брал у кого-нибудь очки и медленно надевал их, а потом снимал и снова надевал. Или просто беседовал с ними. Как-то раз он спросил у Генри:
— Знаешь, что на каждое число есть другое число, вдвое больше?
— Неправда! — воскликнул Генри.
Фейнман ответил, что может это доказать.
— Назови число.
— Миллион!
— Два миллиона, — ответил Фейнман.
— Двадцать семь!
— Пятьдесят четыре, — ответил Фейнман, и так продолжалось до тех пор, пока Генри не уловил суть. Это было первым знакомством ребенка с понятием бесконечности.
Некоторое время, поскольку Фейнман не воспринимал свою работу всерьез, Дайсон относился к ней столь же несерьезно. В письмах родителям он называл Фейнмана «не то гением, не то шутом» (и впоследствии жалел об этих словах). Через несколько дней Дайсон услышал рассказ наведавшегося в Корнелл Вайскопфа об исследованиях Швингера в Гарварде. Он уловил связь между работой Швингера и тем, что говорил Фейнман, хотя последний оперировал совсем другими понятиями. За вспышками и необузданностью Фейнмана он начал замечать наличие метода. И в следующем письме родителям заговорил уже иначе:
«Фейнман — человек, чьи идеи понять столь же трудно, сколь легко понять идеи Бете. По этой причине до сих пор я гораздо большему учился у Бете, чем у него. Но, мне кажется, если я задержусь здесь подольше, то буду работать именно с Фейнманом».
Смутная картинка
Физикам казалось, что их трудности чисто математические: все эти бесконечности, расхождения, формальный подход. Но было еще одно скрытое препятствие, которое редко всплывало в опубликованных работах и устных обсуждениях, — невозможность визуализации. Разве возможно представить атом или электрон в момент излучения им света? Каким должен быть мысленный образ, способный помочь ученому, направив его размышления по верному пути? Первые квантовые парадоксы заставили физиков усомниться в своей способности к интуитивному пониманию, в своей интуиции вообще, и к началу 1940-х годов они почти перестали говорить о визуализации. Казалось, эта проблема больше из области психологии, чем физики.
Визуализация атома по Нильсу Бору — атом, представленный в виде миниатюрной Солнечной системы, — была отвергнута как не соответствующая истине. В 1923 году, на десятую годовщину разработки этой концепции, немецкий квантовый физик Макс Борн восхвалял ее: «Идея о том, что законы микрокосма отражают происходящее в большом мире, видится человеческому уму истинным волшебством». Но уже тогда Борн и его коллеги понимали, что модель Бора — анахронизм. Она выстояла, когда открыли угловой момент и спин, ее включили в стандартную программу по физике и химии для старших классов, но картинка электронов, вращающихся вокруг ядра, больше не соответствовала действительности. На смену ей пришли волны с резонансными модами, вероятностно рассеянные частицы, операторы и матрицы, изменчивые пространства с дополнительными измерениями. Настал момент, когда физики решили полностью отказаться от идеи визуализации. Тон задал сам Бор. На вручении Нобелевской премии за свою модель атома он сказал, что пора отказаться от надежды описать атомную модель путем проведения аналогий с повседневными понятиями. «Мы должны умерить наши требования и довольствоваться формальными концепциями — формальными в том смысле, что они не снабжены визуальной информацией, привычной картинкой…» Такая смена позиции породила немало трений. «Чем больше я размышляю над физической стороной теории Шрёдингера, тем более отталкивающей ее нахожу, — заметил Гейзенберг в 1926 году в разговоре с Паули. — Попробуйте представить вращающийся электрон, чей заряд распространяется в пространстве по осям в четырех-пяти измерениях. То, что Шрёдингер пишет о возможности визуализировать его теорию… я считаю бредом». Как бы высоко ни ценился среди физиков навык концептуализации, который они называли интуицией, сколько бы ни говорилось о разнице физического и формального понимания, вывод напрашивался сам собой: не стоит доверять изображениям субатомной реальности, списанным с земного, повседневного опыта. Бейсбольные мячи, артиллерийские снаряды, планетоиды — квантовые физики-теоретики отвергли все эти модели, отказались от визуализации в виде колесиков и волнистых линий. Отец Фейнмана как-то спросил его (впоследствии Ричард много раз пересказывал эту историю): «Когда атом переходит из одного состояния в другое, он излучает частицу света, называемую фотоном. Это понятно. Фотон в атоме опережает время? Если да, то откуда он берется? Как излучается?» Ни у кого не было картинки, иллюстрирующей это явление — излучение света, взаимодействие материи и электромагнитного поля. А ведь оно было определяющим для квантовой электродинамики.
Вместо картинки возникла бездна — бурлящая, живая, полная вероятностей; неспокойный вакуум новой физики. Некоторые физики, не в силах подобрать даже приблизительный визуальный аналог происходящего в квантовом мире, обратились к новому виду философствования — парадоксальным мысленным экспериментам и спорам о реальности, сознании, причинности и измерении. К концу 1920-х годов эти споры стали неотъемлемым атрибутом интеллектуальной среды; они были провокационными и неразрешимыми и следовали за физикой, как облако пыли за автоколонной. Опубликованная в 1935 году работа Эйнштейна, Подольского и Розена — та самая, благодаря которой у семнадцатилетнего Швингера появился шанс произвести впечатление на Раби, — стала тому ярчайшим свидетельством. В ней приводились примеры двух квантовых систем — возможно, атомов, — связанных в прошлом взаимодействием частиц, но в данный момент разделенных большим расстоянием. Авторы показывали, что простое измерение одного атома из пары повлияет на результаты измерения второго, причем эффект будет мгновенным — быстрее света, то есть, по сути, ретроактивным. Эйнштейн считал, что это компрометирует законы квантовой механики. Бор и более молодые теоретики были настроены более оптимистично, отмечая, что Эйнштейн уже отнес представления о прошлом и о расстоянии в категорию понятий, о которых нельзя говорить с полной определенностью, в классическом духе. В том же ключе была выдержана теория о знаменитом коте Шрёдингера: бедное гипотетическое животное сидело в ящике с детектором, присоединенным к пузырьку с ядовитым газом, и его судьба, таким образом, зависела все от того же квантово-механического явления — излучения фотона атомом. Шрёдингер утверждал, что, несмотря на бойкие вероятностные расчеты ученых — в пятидесяти процентах случаев «да», в пятидесяти «нет», — они по-прежнему не могли визуализировать кота иначе как живым или мертвым.
Со временем физики неохотно примирились с тем, что неспособны выстроить однозначную ментальную модель событий, происходящих в микромире. Используя слова «волна» или «частица» — а использовать оба этих слова приходилось, — они сопровождали их молчаливыми кавычками, словно подразумевая: на самом деле это никакая не волна и не частица. В результате все признали, что отношение ученых-физиков к действительности изменилось. Больше невозможно было предполагать, что существует единственная реальность и что ум человека способен рационально и четко ее осмыслить, а ученый — объяснить. Стало ясно: продукт работы исследователя — теория или модель — рассматривает и интерпретирует опыт способом, который никогда не дает окончательного ответа. Ученые полагались на модели, как человек, пытающийся сориентироваться в темной комнате, опирается на почерпнутый из памяти визуальный образ. Физики начали открыто говорить о том, что создают некий язык — как будто они были не исследователями, а литературными критиками. «Не стоит считать, что задача физики — выявить законы природы, — говорил Бор. — Физика касается лишь того, что можно сказать о природе». И это всегда было так, но на сей раз природа утерла ученым нос.
Однако в конечном счете почти никому из физиков не удалось полностью отказаться от визуализации. Образы были им необходимы. Прагматичные теоретики ценили образ мышления, основанный на видении и чувствовании. Они называли его физической интуицией. Фейнман сказал Дайсону (и тот с ним согласился), что именно благодаря физической интуиции появились великие работы Эйнштейна. Период величия для Эйнштейна закончился, когда тот «перестал мыслить конкретными физическими образами и начал манипулировать уравнениями». Интуиция задействовала не только визуальный, но и слуховой, и кинестетический каналы. Те, кто видел Фейнмана в минуты предельной концентрации, рассказывали о сильном, даже тревожном воздействии этого процесса как физического: создавалось впечатление, что его мозг не ограничивался серым веществом, а заставлял работать все мышцы тела. Сосед Фейнмана по Корнеллскому общежитию как-то открыл дверь и увидел, что Ричард катается по полу рядом с кроватью: так он решал задачу. А когда не катался, то как минимум ритмично бормотал себе под нос или отбивал барабанную дробь кончиками пальцев. В ходе научной визуализации человек часто помещает себя внутрь природной среды: в воображаемый луч света, в релятивистский электрон. Как писал историк науки Джеральд Холтон, это процесс, в котором «карта ума… и законы природы накладываются друг на друга». Для Фейнмана элементы в природе взаимодействовали в ощутимом, меняющемся, порхающем ритме.
Он и сам об этом задумывался; как-то раз даже выписал фрагмент стихотворения Набокова (хотя литература и поэзия совсем его не интересовали): «Пространство — мельтешение в глазах; а время — пение в ушах».
— Вот вы все время твердите о визуализации, — заметил он в разговоре с историком Сильваном Швебером, который брал у него интервью. — Я пытаюсь привнести ясность, но рождается лишь смутная картинка, которая с трудом поддается осмыслению и визуализируется лишь наполовину. Мне представляются дрожащие траектории и извилистые линии. Даже сейчас, рассуждая о функционале влияния, я вижу слияние и собираю образы, словно вещи в мешок, а затем пытаюсь их развить. Я могу их представить, но не могу описать.
— Можно ли сказать, что вы видите решение? — спросил Швебер.
— Скорее лишь его очертания. Пожалуй, такой метод визуализации является интуитивным. Как правило, я пытаюсь представить картинку настолько четкой, насколько это возможно, но иногда могу пойти математическим путем, так как он оказывается более эффективным. Однако при решении некоторых задач я сталкиваюсь с необходимостью задействовать воображение; тогда я обращаюсь к этому методу, прежде чем перейти к математическим расчетам.
Главной сложностью стала визуализация понятия «поле». Однажды Фейнман сказал студентам: «У меня нет подходящего образа для электромагнитного поля, с помощью которого вы могли бы представить суть этого понятия». Пытаясь проанализировать собственный способ визуализировать то, что не поддается воображению, он выяснил нечто странное. Математические символы, которые он использовал каждый день, переплелись с его физическими ощущениями движения, давления, ускорения. Фейнман наделял абстрактные символы физическим смыслом даже тогда, когда он пытался управлять своей необузданной физической интуицией и оперировать этими символами, применяя свои знания.
«Описывая магнитное поле, движущееся в пространстве, я говорю о E- и B-полях и размахиваю руками, поэтому вам может показаться, что я действительно их вижу. Но на самом деле я вижу некие смутные, темные, дрожащие линии, кое-где снабженные стрелочками, исчезающими, если приглядеться внимательнее… Тогда я начинаю путать символы, которые использую для описания объектов, и сами объекты».
И все же Фейнман не мог ограничиться одним лишь математическим методом. В математике поле представляло собой совокупность чисел, каждое из которых было связано с определенной точкой в пространстве. «Это невозможно вообразить», — признался он студентам.
Визуализация необязательно подразумевала построение диаграмм. Как сложное, интуитивное, кинестетическое понимание физики не всегда можно было передать с помощью фигур, составленных из палочек, так и диаграмма не всегда отражала физическую реальность. Визуализация могла иметь форму таблицы или картинки-подсказки. К тому же в квантовой физике диаграммы использовали редко. Правда, был один типичный пример — «лесенка» из горизонтальных линий, изображающая энергетические уровни атома:
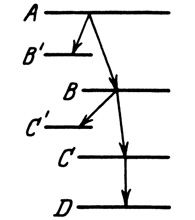
Квантовый скачок, визуализированный в виде лесенки
Квантовый скачок (переход) вниз с одного энергетического уровня на другой сопровождается излучением фотона; поглощение фотона приводит к скачку на верхний уровень (согласно постулатам Бора). На подобных диаграммах фотоны не отображались вовсе, как и на других, еще более неудачных схемах того же процесса.
Фейнман никогда не использовал такие диаграммы, но часто заполнял страницы своих тетрадей рисунками, напоминающими о пространственно-временных траекториях, которые были столь важной частью его принстонской работы с Уилером. Путь электрона на его рисунках изображался прямой линией, которая шла через всю страницу, символизируя движение в пространстве (горизонталь) и во времени (вертикаль). Поначалу Фейнман, как и другие, не отображал излучение фотона; это явление передавалось на картинке как отклонение электрона от намеченной траектории. Такой подход отражал выбранный ученым способ визуализации процесса: Фейнман по-прежнему воспринимал взаимодействие электронов с электромагнитным полем как взаимодействие именно с полем, а не со скоплением частиц — фотонов.
В середине 1947 года после длительных уговоров и даже угроз друзья Фейнмана убедили его опубликовать идеи, о которых он беспрестанно им твердил. Когда публикация наконец увидела свет, диаграмм в ней не было. Новый труд, в основу которого легла частично переработанная дипломная работа, свидетельствовал о том, что фейнмановское понимание проблем квантовой электродинамики стало более зрелым и глубоким. Он объяснял постулаты своей новой теории с беззастенчивой простотой. Для многих физиков эти идеи стали самыми влиятельными из всех, когда-либо опубликованных Фейнманом.
Он утверждал, что разработал альтернативную формулировку квантовой механики в дополнение к тем, что двадцатью годами ранее представили Шрёдингер и Гейзенберг. Он определил понятие амплитуды вероятности для пространственно-временной траектории. В классической механике физики просто складывали вероятности. Например, в бейсболе процент шансов перехода беттера на первую базу считается так: тридцать процентов вероятности попадания по мячу плюс десять процентов вероятности перемещения на базу за болы (четыре неточные подачи питчера подряд) плюс пятипроцентная возможность ошибки. В мире квантовой механики вероятности выражались в виде комплексных чисел, чисел с модулем и фазой, и рассчитывались из квадрата амплитуд. Эта математическая процедура была необходима, чтобы выявить свойство частиц вести себя как волны. Волнам свойственна интерференция. Они могут усиливать или гасить друг друга в зависимости от того, как накладываются их фазы. Свет, соединяясь со светом, может порождать тьму, чередующуюся с яркими полосами, — подобно глубоким бороздам и высоким гребням, образуемым волнами на поверхности озера.
Фейнман описал то, с чем его читатели уже были знакомы, — канонический эксперимент квантовой механики, так называемый эксперимент с двумя щелями, который для Нильса Бора стал иллюстрацией неизбежного парадокса корпускулярно-волнового дуализма. К примеру, поток электронов проходит сквозь две прорези в экране. С противоположной стороны их поступление фиксирует детектор. Достаточно чувствительный прибор способен фиксировать перемещения электронов в виде полета множества пуль; он может быть настроен так, чтобы производить щелчки, подобно счетчику Гейгера. Однако возникающая картина демонстрирует другое пространственное явление: вероятность найти электрон в той или иной точке детектора определяется дифракционной картиной, а точнее — результатом интерференции «электронных» волн, прошедших через щели. Так что же такое электрон — частица или волна? Решением этого парадокса в квантовой механике стал неизбежный вывод: каждый электрон каким-то образом «видит» обе прорези и проходит через них одновременно. В классическом же представлении частица должна проходить только через одну из двух щелей. Однако в процессе эксперимента, когда прорези поочередно закрывали, пропуская поток электронов сначала через щель А, а затем через щель В, интерференции не происходило. Делались попытки «поймать» частицу в момент ее прохождения через одну из щелей, разместив детектор рядом с прорезью, но, казалось, само присутствие детектора разрушало возникавший ранее рисунок.
До сих пор амплитуда вероятности отражала возможность прибытия частицы в определенное место в определенное время. У Фейнмана она стала соответствовать «всему циклу движения частицы», то есть ее пути целиком. Он сформулировал центральный принцип своей квантовой механики: «Вероятность процесса, который может происходить несколькими различными способами, пропорциональна квадрату суммы комплексных вкладов всех альтернативных путей». Эти комплексные числа, эти амплитуды, прежде записывались в терминах классического действия; Фейнман показал, как рассчитать действие для каждой траектории в виде определенного интеграла. И доказал, что этот необычный подход является математическим эквивалентом стандартной волновой функции Шрёдингера, хоть и сильно отличается от нее по духу.
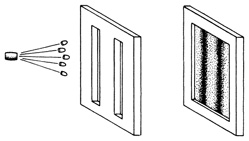
Главная загадка квантовой механики — та, к которой в итоге сводятся все остальные.
Подчиняясь классическим законам механики, оружие, производя выстрел, выпускает пули. Но на пути к цели они сначала должны пройти сквозь экран с двумя щелями. Траектория их движения показывает, что вероятность попадания в цель зависит от места их прохождения. Наиболее вероятно попадание в цель позади одной из прорезей. Вероятность этого равна сумме вероятностей для каждой щели: если бы половину пуль выпустили с открытой левой щелью, а половину — с открытой правой, результат был бы одинаковым.
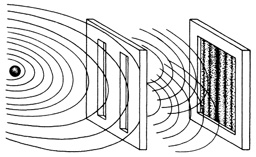
Но когда мы имеем дело с волнами, результат существенно отличается. Если открывать щели по очереди, путь волн будет похож на траекторию пуль: мы увидим два отчетливых пика. Но если обе щели открыты, волны проходят через них одновременно, и происходит интерференция; при совпадении фаз волны усиливают друг друга, при несовпадении — гасят.
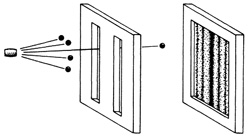
Итак, мы подошли к квантовому парадоксу. Подобно пулям, частицы «выстреливают» в цель каждая по отдельности, но при этом они, как и волны, подвержены интерференции. Если каждая частица проходит через щель по своему индивидуальному пути, что вызывает интерференцию? Хотя электрон и достигает цели в определенной точке в пространстве и времени, оказывается, что каким-то образом он проходит через обе щели, или, если хотите, «ощущает присутствие» в обеих щелях одновременно.
Фейнман не печатался в Physical Review уже более десяти лет — с тех пор, как опубликовал свою дипломную работу. К его огорчению, редакция отказалась печатать этот новый труд. Бете помог ему кое-что переписать, показал, как разделить для читателя старое и новое, после чего Фейнман отправил работу в журнал «Обзоры современной физики» (Reviews of Modern Physics), специализирующийся на ретроспективных исследованиях. Она вышла весной под заголовком «Пространственно-временной подход в нерелятивистской квантовой механике» (Space-Time Approach to Non-Relativistic Quantum Mechanics). Фейнман открыто признавал, что его формулировка квантовой механики не представляет собой ничего нового с точки зрения результатов, но при этом объяснял, в чем состоит достоинство его труда: «Есть ни с чем не сравнимое удовольствие в том, чтобы рассматривать давно известное с новой точки зрения. Кроме того, существуют задачи, решать которые новым способом гораздо удобнее». (Например, при расчете взаимодействия частиц можно избежать трудоемких расчетов с использованием двух различных систем координат.) Читатели — поначалу их были единицы — не обнаружили в его работе замысловатой математики, увидев в ней всего лишь попытку немного иначе взглянуть на известную проблему: ее основа была взята из чистой классической механики и пропущена через призму физической интуиции.
Но были и те, кто сразу распознал потенциал фейнмановских идей, например польский математик Марк Кац. Он слышал лекции Фейнмана об интегралах по траекториям в Корнелле и сразу же заметил сходство его рассуждений с теорией вероятности. Кац в то время пытался развить исследования Норберта Винера по броуновскому движению — хаотичному, беспорядочному движению атомов в процессе диффузии, которое так занимало Фейнмана в ходе его теоретических изысканий в Лос-Аламосе. Винер тоже создал интегралы, суммирующие множество вероятных путей частицы, но в его теории было одно существенное отличие — то, как он рассматривал время. Через несколько дней после выступления Фейнмана Кац разработал новую формулу, получившую название формулы Фейнмана — Каца. Впоследствии она станет одним из самых часто используемых математических инструментов, установивших связь между применением теории вероятности и квантовой механикой. А польский математик будет считать, что его знают прежде всего как «Каца из формулы Фейнмана — Каца»: это открытие затмит все остальные в его карьере.
Фейнмановские интегралы по траекториям — эти суммы траекторий — казались странными даже физикам, привыкшим к теориям со сложным философским смыслом. Они создавали вселенную, где учитывались все потенциальные возможности, где ничего не оставалось скрытым и признавалась каждая вероятность. Фейнман объяснил свою концепцию Дайсону:
«Электрон делает все, что ему вздумается, движется в любом направлении с любой скоростью, вперед или назад во времени — как ему захочется. А потом ты просто складываешь амплитуды и получаешь волновую функцию».
Дайсон с улыбкой ответил, что Фейнман сошел с ума. Но Фейнман интуитивно уловил самую суть эксперимента с двумя щелями, в котором электрон «осознавал» все вероятности.
Попытка Фейнмана познать природу с помощью интеграла по траекториям, его понятие «суммы историй» представляли собой переосмысление принципов наименьшего действия и наименьшего времени. Фейнману казалось, что он открыл глубинные законы, благодаря которым много веков назад возникли принципы механики и оптики, открытые Христианом Гюйгенсом, Пьером де Ферма и Жозефом Луи Лагранжем. Откуда брошенный мяч знает, что должен описать именно эту дугу, максимально сократив действие? Откуда лучу света известно, что он должен выбрать траекторию, сводящую к минимуму время распространения? В ответ на эти вопросы Фейнман представил теорию, которая служила для осмысления не только новых тайн квантовой механики, но и обманчиво невинных задачек, с которыми сталкивается любой начинающий студент-физик. Проходя через воду, свет преломляется под точным углом. От поверхности зеркала он отскакивает, как бильярдный шар. Кажется, что свет движется по прямой. Этот путь — путь наименьшего времени — особенно примечателен, потому что отражает ситуацию, когда вклады соседних траекторий почти совпадают по фазе и потому усиливают друг друга. Но на краю зеркала — вдали от пути наименьшего времени — траектории обнуляются. При этом свет проходит всеми возможными путями. Фейнман показал это; он доказал, что траектории, которые на первый взгляд кажутся несущественными, всегда присутствуют в общей картине, затаившись где-то на заднем плане; их вклады не проходят незамеченными, они готовы заявить о себе в любой момент такими явлениями, как миражи и дифракционная решетка.
Студентов, изучающих оптику, в то время учили альтернативному объяснению этих явлений, представляя свет волной, подобной тем, что образуются в воздухе и воде. Фейнман категорически отмел эту точку зрения. Волнообразность — внутреннее свойство фазы, которой обладает амплитуда. Когда-то давно, вместе с Уилером, Фейнман мечтал вовсе исключить из рассуждений поле. Это оказалось невозможным. Поле прочно укоренилось в сознании физиков. Без него было не обойтись; более того, число полей постоянно множилось. Появление новых частиц, например мезонов, означало возникновение нового поля — словно дополнительного слоя прозрачного пластика; частица была его квантованным проявлением. И все же теория Фейнмана сохранила признаки своего первоначального скелета, хотя от самого скелета он давно отказался. Ее «действующими лицами» снова были частицы, и на этот раз их роль вырисовывалась более отчетливо. Это привлекло к ней внимание физиков, ищущих опору в визуализации, потерявшихся в мире мыслительных экспериментов, где все больше властвовали облачные следы, номенклатуры и поведение частиц.
Слава Швингера
Интегралы по траекториям Фейнмана были частью разрозненного арсенала идей и методов, которые были им накоплены, но не сведены в единую систему. Это была его личная, «частная» физика. В своих исследованиях он часто полагался на догадки или, по его собственному выражению, «полуэмпирические шалости». Его интересовал лишь результат, методы же представляли собой бессвязную мешанину; он с трудом мог объяснить и тем более обосновать свои выводы даже самым своим сочувствующим слушателям — Бете и Дайсону. Осенью 1947 года Фейнман посетил публичную лекцию Бете, в которой тот описывал свой подход к Лэмбовскому сдвигу. В заключение Бете подчеркнул необходимость разработать более надежный способ сделать теорию конечной — способ, который не противоречил бы теории относительности. Тут Фейнман понял, что сможет сделать необходимые вычисления и внести исправления. Он пообещал Бете к утру дать ответ.
Но к утру он понял, что не располагает достаточной информацией о том, как Бете вычислил самоэнергию электрона, и поэтому не может перевести свои наработки на нормальный язык физики. Они вместе постояли у доски: Бете объяснил свои расчеты, Фейнман попытался изложить свой метод, но в ответе, который получился в итоге, обнаружились не скромные, как у Бете, а чудовищные расхождения. Вместе с тем, размышляя о проблеме с физической точки зрения, Фейнман был убежден, что расхождений не будет.
В последующие дни он вспомнил все, что знал о самоэнергии. Переписав свои уравнения с учетом наблюдаемой, «одетой», массы электрона вместо «голой», он выяснил, что решение, как он и думал, будет конечным. Тем временем Итаки достигла новость (ее принесли Вайскопф и Бете) о прорыве, сделанном Швингером в Кембридже. К тому моменту, когда в конце осени стало известно, что Швингер сумел рассчитать магнитный момент электрона — еще одну маленькую экспериментальную аномалию, недавно обнаруженную в лаборатории Раби, — Фейнман уже успел сделать то же самое. Сложные вычисления Швингера убедили ведущих физиков в том, что теория не зашла в тупик. «Господь велик!» — писал Раби Бете со свойственным ему сарказмом. А Бете отвечал: «Поистине замечательно, что твои эксперименты позволили взглянуть на теорию под совершенно новым углом; за относительно короткое время она стала развиваться. Я испытываю такое же волнение, как в дни зарождения квантовой механики».
Фейнман испытывал растущее чувство соперничества по отношению к Швингеру, и его это все больше раздражало. Ему казалось, что у него есть своя квантовая электродинамика, а у «Швингера — Вайскопфа — Бете», которых он считал командой — своя. В январе состоялась заседание Американского физического общества в Нью-Йорке, и Швингер на нем блистал. Его проект был далек от завершения, но он внедрил в стандартную квантовую механику новую идею перенормировки и сумел продемонстрировать ряд впечатляющих выводов. Он показал, что аномальный магнитный момент (например, Лэмбовский сдвиг) возникает вследствие взаимодействия электрона с собственным полем. Его лекция собрала толпу народа; зал был набит битком. Многие физики были вынуждены стоять в коридорах и слышали лишь взрывы аплодисментов (и смущенный смех, раздавшийся в тот момент, когда Швингер в конце своей речи произнес: «Совершенно ясно, что…»). Лекцию решили повторить в тот же день в Колумбийском университете; последовали спешные приготовления. На этой лекции побывал Дайсон. Оппенгеймер сидел в первом ряду и, не стесняясь, курил трубку. Когда настало время для вопросов и ответов, Фейнман встал и заявил, что получил аналогичные результаты и мог бы внести небольшую корректировку. И тут же пожалел о своих словах. Ему показалось, что они прозвучали как слова маленького мальчика, пролепетавшего: «Папа, я тоже так умею!» Той зимой еще мало кто догадывался, насколько сильным было соперничество между ним и Швингером, но одного раздосадованного замечания, высказанного Фейнманом своей девушке, было достаточно, чтобы та поняла источник его разочарования и разобралась в ситуации.
«Мне жаль, что эксперимент, над которым ты так долго работал, буквально украден кем-то другим, — ответила она. — Я понимаю, как тебе неприятно. Но, Дик, ведь конкуренция делает жизнь гораздо интереснее». И поинтересовалась: почему бы ему и его сопернику не объединить усилия и не начать работать вместе?
Не только Швингер и Фейнман пытались найти объяснение экспериментам с Лэмбовским сдвигом и магнитным моментом электрона и произвести соответствующие вычисления. Другие физики-теоретики взяли на вооружение подход Бете — те самые вычисления, которые он набросал на клочке бумаги. Они не видели необходимости в создании монументальной теории, новой квантовой электродинамики; ведь достаточно было внедрить технику перенормировки в существующую физику, и нашелся бы правильный ответ. Две команды ученых добились в этом успеха независимо друг от друга, придя к более совершенному, чем у Бете, решению, которое учитывало рост величин на околосветовой скорости. Но одна команда — Вайскопф и аспирант Брюс Френч — совершила роковую ошибку, в нерешительности посоветовавшись со Швингером и Фейнманом перед публикацией своих открытий. Поглощенные своими более амбициозными проектами, они предостерегли Вайскопфа, сказав, что тот допустил неточность в расчетах одного маленького коэффициента. Вайскопф решил, что столь блестящие молодые ученые не могут ошибаться оба сразу, и отложил публикацию. Прошли месяцы, прежде чем Фейнман позвонил Вайскопфу, извинился и сказал, что его вычисления были верны.
Что касается собственной теории Фейнмана, разработкой которой он занимался, прорыв в ней произошел, когда он столкнулся с щекотливой темой антиматерии. Первая античастица — антиэлектрон, или позитрон — была описана менее двадцати лет назад. Это был знак «минус» из уравнений Дирака, следствие симметрии между позитивной и негативной энергией. Дирак, будучи вынужден как-то объяснить наличие «дыр» в океане энергии, в 1931 году отметил, что «дыра, если таковая обнаружится, является новым видом частиц, неизвестным экспериментальной физике». Впрочем, неизвестным этот вид пробыл лишь несколько месяцев: Карл Андерсон из Калифорнийского технологического нашел следы таких частиц в облачной камере, построенной для обнаружения космических лучей. Частица выглядела как электрон, но, двигаясь в магнитном поле, отклонялась вверх, а не вниз.
Четкие фотографии и броское название, придуманное для новой частицы редактором журнала против воли Андерсона, узаконили существование позитрона. Физики-теоретики больше не могли его игнорировать. При столкновении электрона с его «побратимом» из мира антивещества высвобождалась энергия в виде гамма-лучей. Или, на языке Дирака, который представлял себе вакуум как живой бурлящий океан, испещренный дырами или пузырьками, электрон проваливался в дыру и заполнял ее собой, вследствие чего и дыра, и электрон исчезали. Продолжив изучение снимков космических лучей, экспериментаторы выяснили, что есть и обратный процесс: гамма-луч, то есть высокочастотная частица света, был способен спонтанно произвести пару частиц — один электрон и один позитрон.
В теории Дирака наметились проблемные места: в ней, как и во всей его физике, возникали нежелательные бесконечности. Простейшее описание вакуума — пустое пространство в условиях абсолютного нуля — предполагало наличие бесконечной энергии и бесконечного заряда. А с практической точки зрения человека, пытающегося вывести уравнение, бесконечность частиц была чревата неприятными последствиями. В поисках выхода из этой ситуации Фейнман в очередной раз обратился к своей работе с Уилером в Принстоне и восприятию времени как потока, текущего в обоих направлениях. Он снова предложил пространственно-временное решение, в котором позитрон был электроном с противоположным знаком времени. Геометрия этого решения была проста, но весьма необычна, и Фейнману стоило большого труда подобрать метафору для ее описания:
«Представьте, что в куб с коллодием поместили черную нить, после чего коллодий отвердевает, — писал он. — Нить тянется сверху вниз произвольным образом. Затем куб нарезают по горизонтали на тонкие квадратные секции; из этих срезов, как из последовательно сменяющих друг друга кадров, составляют фильм». На каждом таком срезе будет присутствовать точка, и она будет перемещаться, шаг за шагом повторяя траекторию нити. А теперь представьте, объяснял Фейнман, что нить в кубе изогнулась в форме буквы N. Стороннему наблюдателю, который видит только срезы, но не нить целиком, эта картина напомнит образование пары «частица/античастица»:
«На последовательных срезах сначала будет видна лишь одна точка, но потом появятся еще две — срезанные участки изогнувшейся нити. Все три точки будут какое-то время двигаться вместе, затем две из них сойдутся и «обнулятся», и на последних кадрах вы опять увидите одну точку».

С помощью обычных уравнений, которые позволяют вычислить движение электрона, можно рассчитать и эту модель, хотя понадобится пройти «более сложный путь в пространстве и времени, чем тот, к которому мы привыкли». Сравнение с нитью не нравилось Фейнману; он искал метафоры, которые точнее бы выразили его точку зрения, запечатлели бы саму суть различия между траекторией нити «в срезе», то есть в конкретный момент времени, и явлением в целом. Но потом студент Корнелла, в войну служивший пилотом бомбардировщика, предложил сравнение, которое Фейнман позже использовал в своей работе и которое стало знаменитым.
Итак, пилот следит за дорогой через прицел низко летящего бомбардировщика и вдруг видит не одну, а три дороги. Он испытывает смятение, которое вскоре проходит, так как два новых «разветвления» сходятся и исчезают; пилот понимает, что мгновением раньше пролетел место, где дорога поворачивает в обратном направлении, изгибаясь в форме буквы N. Тот участок, где дорога идет назад, соответствует позитрону — он возникает одновременно с первым электроном, движется и аннигилирует с другим электроном.
Так Фейнман описал картину в целом. Метод интегралов по траекториям хорошо подходил для этой модели: еще по своей работе с Уилером он знал, что сумма фаз ближайших траекторий применима и к «обратному времени». Он также нашел способ разрешить осложнения, возникшие из-за принципа запрета Паули — фундаментального закона квантовой механики, согласно которому два электрона не могут одновременно находиться в одном и том же квантовом состоянии. Фейнман весьма оригинально обошел этот принцип — постановил, что, хотя в ранних вычислениях участвовали две частицы, на самом деле это была одна частица, двигающаяся по зигзагообразной траектории во временном срезе. «Обычная теория скажет, что это невозможно, потому что в отрезок времени между ty и tx два электрона не могут находиться в одном и том же состоянии, — записал он в тетради. — Но мы заявляем, что это один и тот же электрон, и таким образом принцип Паули перестает действовать». Объяснение, словно взятое из научно-фантастического романа о путешествиях во времени, — едва ли физики были готовы его принять. Фейнман отдавал себе отчет в том, что предлагает радикально отступить от общепринятого понимания времени. Он нарушал повседневную интуитивную логику, гласящую, что будущего еще не существует, а прошлое уже прошло. В свое оправдание он мог сказать лишь одно: физическое время перестало соответствовать времени «психологическому» — законы микромира не делали различий между прошлым и будущим, а Эйнштейн уничтожил понятие абсолютного времени, не зависящего от наблюдателя. Вместе с тем Эйнштейн и помыслить не мог, что частицы способны развернуться и поплыть против течения времени. Фейнману осталось лишь подчеркивать необходимость такого переосмысления. «Для физики может оказаться полезным рассмотрение событий во всех временных пластах одновременно и понимание того, что в каждый отдельный момент времени мы осознаём лишь то, что уже случилось», — писал он.
Грохот моих шестеренок
Весной 1948 года Швингеру и Фейнману предстояла очередная конференция — продолжение элитной встречи на Шелтер-Айленде. Мероприятие запланировали на конец марта; для него был арендован курортный отель в горах Поконо в Пенсильвании. Все было как в прошлый раз: идиллическая обстановка, небольшой список участников и серьезная повестка. Снова должны были приехать Ферми, Бете, Раби, Теллер, Уилер и фон Нейман; председателем назначили Оппенгеймера. Кроме того, в этот раз ждали двух гигантов довоенной физики: Дирака и Бора.
Они собрались 30 марта в холле отеля, под старой зеленой башней с часами. Из окон открывался вид на поле для гольфа и километры лесистых гор. Конференция началась с доклада, посвященного последним новостям о треках частиц в космических лучах и ускорителе в Беркли. Ученые обещали, что к осени синхротрон, снабженный пятиметровым магнитом, разгонит протоны до значений энергий в 350 миллионов электронвольт. Этого будет достаточно для выделения огромного числа новых элементарных (так казалось ученым) частиц — мезонов, содержащихся в космических лучах и в данный момент представляющих самый большой интерес для исследователей. Чем ждать, пока образцы частиц поступят в облачные камеры из космоса, экспериментаторы лучше создадут их самостоятельно.
Анализируя данные, полученные в результате изучения космических лучей, ученые столкнулись с проблемой: оказалось, что между ожидаемой и реальной силами взаимодействия мезонов с другими частицами имелось огромное расхождение. На предыдущей конференции молодой физик Роберт Маршак высказал мнение, которое в 1947 году требовало от ученого гораздо больше мужества и смекалки, чем спустя двадцать — тридцать лет: он предположил, что существуют две разновидности частиц и что эти группы взаимодействуют друг с другом. Не один мезон, а два! — стоило только высказать это предположение, и оно стало очевидным. Фейнман торжествующе заявил, что новую частицу следует назвать маршаком. Благодаря развитию технологий реестр новых частиц насчитывал уже почти двузначное число. На открытии конференции в Поконо экспериментаторы разогревали публику демонстрацией слайдов с наиболее характерными изображениями — впечатляющими треками частиц, похожими на следы разбежавшихся кур. На этих снимках не было полей, матриц, операторов, зато геометрия рассеяния частиц была представлена достаточно отчетливо.
На следующее утро пост докладчика занял Швингер. Он презентовал «полную» теорию квантовой электродинамики, которая, как он подчеркнул в самом начале, соответствовала двойному критерию «релятивистской инвариантности» и «калибровочной инвариантности». Выполненные в соответствии с ней вычисления выглядели одинаково вне зависимости от скорости и фазы частиц. Инвариантность гарантировала, что теория останется неизменной, какой бы ни была случайная позиция наблюдателя: так на длительность отрезка времени от рассвета до заката не влияет то, перевели вы часы на час вперед, чтобы продлить световой день, или нет. Теория обеспечивала независимость расчетов от определенной системы координат — «калибра». По словам Швингера, он рассматривал квантованное электромагнитное поле, в котором «каждая малейшая единица пространства считается частицей» — частицей с большей математической силой и меньшей визуальной ощутимостью, чем в физике вчерашнего дня. Далее он представил новые сложные вычисления и начал демонстрировать применение своей теории на конкретном примере, показывая взаимодействие электрона с его собственным полем. Его почтенные слушатели, скорее всего, ничего не поняли, но, в отличие от привычной Швингеру аудитории, их было не так легко запугать, поэтому его воодушевленную речь не раз прерывали. Сам Бор задал ему вопрос — Швингеру это не понравилось, и он резко его оборвал, а затем продолжил свою речь, пообещав, что все станет ясно в свое время. Как всегда, он не пользовался записями и подчеркивал это; почти вся его лекция была посвящена формулировкам, он выводил одно уравнение за другим. Это был настоящий математический марафон, затянувшийся почти до вечера. Бете отметил, что критики притихли, когда Швингер перешел к математическим формулам; вопросы возникали лишь тогда, когда тот начинал объяснять чисто физические понятия. Он поделился этим наблюдением с Фейнманом и посоветовал ему избрать аналогичный, математический подход к своему докладу. Глядя на своих знаменитых коллег, Ферми с некоторым удовлетворением отметил, что те начали терять нить. Лишь он и Бете до самого конца внимательно слушали Швингера.
Затем настала очередь Фейнмана. Он нервничал. Ему показалось, что лекция Швингера, по всем признакам блистательная, была принята не очень хорошо (но он ошибался: Швингер произвел неизгладимое впечатление на всех, и, главное, на Оппенгеймера). По совету Бете он полностью изменил ход доклада. Изначально Фейнман планировал излагать свои идеи с точки зрения физики; математические формулы у него тоже имелись, хоть и не столь изящные, как у Швингера, но, как и у Швингера, они во многом были понятны лишь самому автору. Он мог объяснить свои методы с помощью формулировок, но не мог обосновать сами математические вычисления. Он пришел к имеющимся результатам путем проб и ошибок и знал, что его формула точна, так как проверил ее на множестве задач, в том числе на задачах Швингера — и она сработала. Но доказать, что она работает, и связать ее со «старой» квантовой механикой он был не в состоянии. Тем не менее он последовал совету Бете и начал с уравнений, заявив: «Математическая формула, которую я сейчас вам покажу, решает все нерешенные задачи квантовой механики».
Фейнман всегда говорил друзьям, что может рассказывать о физике кому угодно — неважно, кем были его слушатели. Он любил вспоминать о том, как Нильс Бор в Лос-Аламосе отметил его как молодого человека, который не боялся оспаривать мнение старших. Время от времени Бор обращался к Фейнману за личной консультацией, часто через своего сына Оге, тоже физика, но так до конца и не проникся к нему полной и безоговорочной симпатией. Бору претила «американистость» Фейнмана, его чрезмерный энтузиазм, манеры рубахи-парня. Сейчас, в конце затянувшегося дня, сидя среди двадцати шести других уважаемых ученых, Бор ждал. Фейнману никогда не приходилось выступать перед таким скоплением светлых научных умов — даже в Принстоне, когда он читал лекции в присутствии Эйнштейна и Паули. Он создал новую квантовую механику, почти не зная старой, за исключением работ Дирака и Ферми, которые он прочитал и на которые опирался; оба ученых сейчас сидели перед ним. Были здесь и его учителя Уилер и Бете. А также Оппенгеймер, который создал одну бомбу, и Теллер, строивший другую. Для них он был многообещающим и бесстрашным юным светилом. Через семь недель ему исполнялось тридцать лет.
Швингер впервые слышал теорию Фейнмана. Она показалась ему интеллектуально отталкивающей, хотя тогда он ничего не сказал (позже они по-дружески сравнят свои методы и обнаружат, что сходятся почти во всем). Ему казалось, что Фейнман выстраивает сеть из догадок и интуитивных предположений, напоминавшую сырой каркас из поперечных и продольных балок. Бете прервал его лишь однажды, почувствовав, что слушатели потерялись в деталях, и попытался вернуть Фейнмана к основным положениям теории. Тот объяснил свои интегралы по траекториям, оставшиеся совершенно непонятыми, и позитроны, путешествующие во времени, — идею еще более чуждую. Теллер отметил явное нарушение принципа запрета и не согласился с неубедительным оправданием Фейнмана. У последнего же сложилось впечатление, что у каждого из присутствующих есть свой любимый принцип или теорема, а он нарушил их все. Дирак спросил: «Ваша теория унитарна?» Фейнман даже не понял, что он имеет в виду. Дирак объяснил: матрица, несущая объект из прошлого в будущее, должна хранить точную информацию о полной вероятности. Но у Фейнмана не было такой матрицы. Суть его подхода заключалась в том, что он рассматривал прошлое и будущее вместе; его объекты могли свободно передвигаться вперед и назад во времени по одному лишь своему желанию. Его не понимали. Наконец, когда он нарисовал на доске диаграммы — схематичные траектории частиц — и попытался продемонстрировать свой метод суммирования амплитуд различных траекторий, Бор поднялся с места. Разве Фейнман не проигнорировал центральный принцип квантовой механики, сформулированный еще двадцать лет назад? Совершенно очевидно, что эти траектории противоречат принципу неопределенности. Он подошел к доске, попросил Фейнмана отойти в сторону и начал объяснять. Уилер, делавший заметки, быстро записал: «Бор хотел знать, действительно ли эта теория рассматривает ту же физику, что и теория Дирака, или же физическая ее часть недостаточно продумана». Бор продолжал рассуждать несколько долгих минут. Тогда-то Фейнман и понял, что потерпел неудачу. В тот момент его это очень огорчило. Но позже он заметит: «Я рассказал им слишком много. Грохот моих шестеренок слишком далек от них».
«Кроме того, Фейнман представил свою теорию»
После конференции Уилер взял на себя задачу по распространению новейших научных данных. В этом его ограничивали лишь технологии того времени. Вернувшись в Принстон, он подрядил своих аспирантов в печатники. Те вручную, страница за страницей, перенесли его конспекты на бланки мимеографа и напечатали несколько десятков экземпляров, отчего их локти надолго окрасились в фиолетовый. В течение долгого времени эти самиздатовские брошюры были единственным способом ознакомиться с новой ковариантной квантовой электродинамикой Швингера. «Альтернативной формулировке» и любопытным диаграммам Фейнмана в ней было отведено лишь несколько страниц. Дайсон с жадностью читал эти заметки. Бете пытался раздобыть для него приглашение в Поконо («Представляете, как меня это обрадовало, как я был польщен?» — писал Дайсон родителям), но Оппенгеймер отказался рассматривать кандидатуру студента.
Фейнману поручили написать отчет нетехнического характера о встрече в Поконо для нового профильного журнала «Физика сегодня» (Physics Today) (как он надеялся, анонимно). В своей статье он разъяснил перенормировку по Швингеру, заключив ее словами:
«Большая часть конференции была посвящена лекции Швингера и последующему обсуждению его находок. Как выразился один участник, “на обсуждения осталось не так много времени, ведь нам пришлось учить физику”. Он имел в виду новую работу Швингера».
«Кроме того, Фейнман представил свою теорию, в которой электродинамические уравнения изменены таким образом, чтобы все величины, в том числе инертность (масса) электронов, оказались конечными. Результаты этой теории согласуются с выводами Швингера, но не имеют столь же законченного характера».
В качестве поощрительного приза Фейнмана попросили помочь в выборе кандидата на получение новой премии, учрежденной Национальной академией наук за «выдающийся вклад в наше понимание природы света». Увидев имя Фейнмана в списке экспертов, Швингер догадался, что премия достанется ему, и оказался прав. Ведь что еще, как не свет во всех его обличьях, является главным предметом изучения квантовой электродинамики?
Пожалуй, никто другой не находился под столь сильным впечатлением от Швингера (и столь же слабым — от Фейнмана), как Оппенгеймер. А по возвращении в Принстон он, к своему изумлению, нашел подтверждение теории Швингера в письме от японского физика-теоретика Синъитиро Томонаги, чей путь к славе начался со слов: «Я взял на себя смелость и отправил вам копии нескольких своих работ и конспектов…»
Японские физики стали значимыми фигурами в мировом физическом сообществе лишь недавно, в 1930-х годах. Хидэки Юкава из Киотского университета первым предположил, что «переносчиком» ядерной энергии, связывающим протоны в атомном ядре, может быть некая тяжелая, недолговечная и еще не открытая частица. Затем началась война, и Япония оказалась отрезанной от остального мира. Даже теперь, когда война закончилась, связь с оккупированной Японией восстанавливалась медленно. О Лэмбовском сдвиге в Киото и Токио узнали не от американских физиков, не из научных бюллетеней, а из небольшой заметки в обычном новостном журнале.
Томонага был уроженцем Токио и выпускником Киотского университета, одноклассником и другом Юкавы. На него глубоко повлиял Дирак: Томонага принадлежал к небольшой группе ученых, которые перевели знаменитый учебник британского физика на японский. В 1937 году он отправился в Германию и учился у Гейзенберга; с началом войны вернулся домой, по пути заехав в Нью-Йорк и посетив Всемирную выставку. Он разработал теорию «супермножественного времени», согласно которой каждая точка поля обладает собственными «часами». Несмотря на кажущуюся абсурдность попыток манипулировать бесконечным числом временных переменных, теория оказалась рабочей. Разрабатывая свою концепцию, Томонага оказался практически на той же территории, которую осваивали его коллеги из Европы и Америки, однако в своих исследованиях он чувствовал себя куда более одиноким, и даже учеба в Германии не избавила его от этого ощущения. Иногда он описывал свое мрачное настроение в дневнике:
«После ужина я снова занялся физикой, но вскоре сдался. Кажется, какой-то злой рок мешает моей работе. Без всякой видимой причины меня охватило уныние, и я пошел в кино… Вернувшись, почитал научный сборник, но мало что понял… Почему в природе всё не может быть яснее и доступнее для понимания?.. Занявшись вычислениями, я обнаружил, что интегралы расходятся: в результате я получаю бесконечность. После обеда пошел прогуляться. На улице жгучий мороз… Все мы стоим на разделительной полосе, откуда невозможно увидеть будущее. Нам не стоит слишком тревожиться из-за результатов, хотя они могут существенно отличаться от ожидаемого…»
Это чувство эмоциональной опустошенности, охватывавшее его время от времени, не шло ни в какое сравнение с тем, что ему пришлось пережить в первые месяцы после японской капитуляции. Нехватка продовольствия и жилья в Японии затмила все остальное. Томонага жил в «куонсетской хижине» — времянке из гофрированной стали — на территории Токийского университета. В ней же он обустроил кабинет. Вместо мебели были татами.
Хотя Оппенгеймер ничего не знал об условиях, в которых жил Томонага, ему было хорошо известно о тяготах, постигших Японию из-за того, что он и его коллеги сотворили в Лос-Аламосе. Он хотел, чтобы физика осталась международной — в данный момент, казалось, в ней воцарились американцы. Так что Томонага написал ему в самый подходящий момент. Из письма ясно следовало, что японский физик не только пришел к тем же основным выводам, что и Швингер, но сделал это раньше. Он не публиковал свою работу и, в отличие от Швингера, не дал ее детального обоснования, но он был первым. Оппенгеймер тут же выразил Томонаге свое одобрение, разослав письма всем участникам конференции в Поконо. «Мы выслушали прекрасный доклад Швингера, — написал он, — и потому сможем оценить это независимое открытие». Для Дайсона, пытавшегося разобраться в новых теориях, представленных в Поконо, откровением в работах Томонаги стала их красивая простота. Он осознал, что теперь наконец ему стали понятны идеи Швингера, которые вряд ли нуждались в столь сложных обоснованиях. Изучая конспекты из Поконо, многие аспиранты пришли к такому же выводу, несмотря на дифирамбы Швингеру со стороны их наставников. Позднее Дайсон процитировал слова одного «недоброжелательного критика», который сказал: «Кто-то печатает свои работы, чтобы рассказать, как это сделать; Джулиан Швингер публикуется, чтобы показать, что только он один может это сделать». Швингер словно поставил своей целью достичь максимально возможного соотношения уравнений к тексту, и его сочинения стали серьезным испытанием для наборщиков Physical Review.
Иногда среди аплодисментов Швингеру раздавалась критика: суть замечаний сводилась к тому, что он бездушный Паганини, вместо музыки ослепляющий слушателей своей техникой; что он больше математик, чем физик; что он слишком старательно сглаживает углы. «Полагаю, меня обвиняют в том, что я представил законченную сложную математическую формулу, за которой не видно физических открытий, ставших для нее строительным материалом», — говорил он позднее.
Да, он убрал те самые «балки». Ему никогда не нравилось демонстрировать черновой ход своей мысли — так же, как он предпочитал не показывать конспекты своих лекций слушателям. Но, если бы ему не хватало физической интуиции, никакая математическая мысль не помогла бы ему соединить относительность и квантовую электродинамику. За всеми его формулами крылось глубокое, историческое понимание природы частиц и полей. Для Швингера перенормировка была не просто математическим фокусом. Она означала новый этап в понимании того, что такое частица. И если бы он сформулировал свое главное открытие повседневным языком, который, по его мнению, был недостаточно выразительным, оно звучало бы так:
«О чем мы говорим — о частицах или о волнах? До недавнего времени ученые считали, что их уравнения непосредственно касаются явления, называемого в физике частицами, — например, уравнение Дирака, которое должно описывать атом водорода. Но применительно к теории полей уравнения характеризуют всего лишь один из подуровней. Экспериментально мы рассматриваем частицы, а теоретически с помощью старых формул описываем поля. Говоря о полях, мы предполагаем, что можно описать и каким-то образом ощутить происходящее во всех точках пространства в любой момент времени; говоря о частицах, мы просто берем образец поля и замеряем его в конкретный момент времени.
Свойство частицы — последовательность. Мы понимаем, что перед нами частица, лишь когда по прошествии времени она остается на месте. Это явление подразумевает непрерывность присутствия в пространстве и времени. Но если мы производим измерения в разные моменты, не связанные друг с другом, откуда нам знать, что мы имеем дело с частицами? Эксперименты позволяют исследовать поле лишь приблизительно, рассматривая большие участки пространства в течение продолжительного времени.
Суть перенормировки заключается в том, чтобы перейти с одного уровня описания на следующий. Начиная выводить уравнения для поля, вы оперируете на уровне, где нет частиц: они появляются лишь тогда, когда уравнения поля решены. Но изначально в уравнениях отсутствуют свойства, приписываемые частицам, — заряд и масса.
Кто-то скажет: “В ваших уравнениях есть расхождения, вам нужно их исправить их”. Но это всего лишь форма, а не суть перенормировки. Суть в том, что теории Максвелла и Дирака описывают не электроны, позитроны и фотоны, а гораздо более масштабные вещи».

