Лекция 3. Великие законы сохранения
Изучая физику, вы обнаруживаете, что существует огромное количество сложных и очень точных законов – законы гравитации, электричества и магнетизма, законы ядерных взаимодействий и т. д. Но все это многообразие отдельных законов пронизано некими общими принципами, которые так или иначе содержатся в каждом законе. Примерами таких принципов могут служить законы сохранения, некоторые свойства симметрии, общая форма квантовомеханических принципов и тот приятный для одних и досадный для других факт, что все законы являются математическими. В этой лекции я хочу поговорить о законах сохранения.
Физик употребляет обычные слова необычным образом. Для него закон сохранения означает, что существует число, которое остается постоянным вне зависимости от того, когда вы его подсчитаете – скажем, сейчас или через некоторое время, после того как в природе произойдет множество изменений. Вот, например, закон сохранения энергии. Имеется величина, которую вы можете вычислять по определенным правилам, и ответ у вас всегда будет одинаковым, что бы ни случилось.
Понятно, что такие принципы могут оказаться полезными. Предположим, что физика, или, вернее, природа, – это огромная шахматная доска с миллионами фигур и мы пытаемся выяснить законы движения фигур. Великие боги, сидящие за доской, играют очень быстро, и нам трудно уследить за их ходами. Все же мы улавливаем некоторые правила – те правила, для выяснения которых не обязательно следить за каждым ходом. Например, предположим, что на доске стоит только один слон, белопольный. Он движется только по диагонали и поэтому всегда остается на белых квадратах. Если мы отвернемся, а затем посмотрим снова на доску, за которой играют боги, то белопольный слон будет по-прежнему стоять на доске, может быть в другом месте, но все равно на белом квадрате. Такова природа законов сохранения. Мы можем узнать кое-что об игре, не вдаваясь в доскональное ее изучение.
Правда, в шахматах этот закон может оказаться не таким уж полезным. Если мы отвернулись надолго, то может случиться, что за это время слона успели съесть, пешка прошла в ферзи и Бог решил, что выгоднее иметь слона вместо ферзя, а слон этот оказывается чернопольным. К сожалению, может выясниться, что некоторые из наших сегодняшних законов физики также несовершенны, но я опишу их вам такими, какими мы видим их в настоящее время.
Я сказал, что мы употребляем обычные слова в качестве научных терминов, а в заглавии этой лекции стоит слово «великий» – «Великие законы сохранения». Это не термин: я вставил его лишь затем, чтобы придать заглавию более патетическое звучание, и вполне мог бы назвать лекцию просто «Законы сохранения». Есть несколько законов сохранения, которые верны лишь приблизительно, но иногда оказываются полезными, их мы могли бы назвать «малыми» законами сохранения. Позже я расскажу об одном или двух из них. Но основные законы, которым посвящена эта лекция, насколько нам известно сегодня, совершенно точны.
Проще всего понять закон сохранения электрического заряда; с него я и начну. Существует число, полный электрический заряд мира, которое остается постоянным, что бы ни произошло. Если вы теряете заряд в одном месте, то находите его в другом. Сохранение относится только к полному электрическому заряду. Это опытным путем установил Фарадей. Он экспериментировал с огромным металлическим шаром, к наружной поверхности которого был присоединен очень чувствительный гальванометр, чтобы следить за зарядом на поверхности; гальванометр был такой, что даже небольшой заряд давал сильные отклонения. Внутри шара Фарадей собрал разнообразное электрическое оборудование. Он создавал заряды, натирая стеклянные палочки кошачьим мехом, и строил большие электростатические машины, так что внутренность шара походила на лабораторию из фильма ужасов. Но в ходе всех его экспериментов на поверхности не появлялось никакого заряда; создать заряд было невозможно. Хотя стеклянная палочка заряжалась положительно, когда ее терли кошачьим мехом, мех получал точно такое же количество отрицательного заряда, и суммарный заряд всегда был равен нулю. Если бы внутри шара заряд создавался, то гальванометр, присоединенный снаружи, показал бы это. Итак, полный заряд сохраняется.
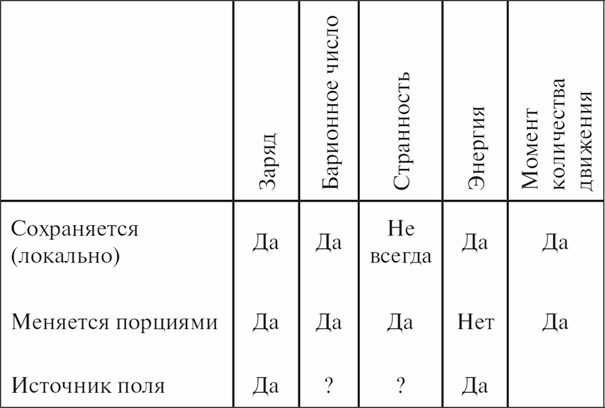
Это нетрудно объяснить на очень простой модели, совсем не математической. Предположим, что мир состоит из частиц двух видов, электронов и протонов, – было время, когда он действительно представлялся людям настолько простым, – и предположим, что электроны несут отрицательный заряд, а протоны – положительный, так что мы можем их разделить. Мы можем взять кусок материала и отнять у него часть электронов или, наоборот, добавить. Но если считать, что сами электроны неизменны, не исчезают и не распадаются (это очень простое предположение, не имеющее отношения к математике), то разность между общим числом протонов и общим числом электронов меняться не будет. Больше того, в нашей простой модели не будет меняться ни одно из этих двух чисел. Но вернемся к зарядам. Вклад протонов положителен, а электронов – отрицателен, и если эти частицы не создаются и не уничтожаются поодиночке, то полный заряд будет сохраняться. В табл. 1 я перечислил некоторые сохраняющиеся величины; первая из них – заряд. Против вопроса, сохраняется ли заряд, я пишу «да».
Такая теоретическая модель очень проста, но со временем было обнаружено, что электроны и протоны нельзя считать постоянными и неизменными. Например, частица, называемая нейтроном, может распадаться на протон и электрон плюс что-то еще, о чем мы поговорим позже. Правда, оказывается, что нейтрон электрически нейтрален. Поэтому, хотя протоны и электроны не неизменны в том смысле, что их можно создать из нейтрона, заряд все равно сохраняется. При распаде нейтрона мы начинаем с нулевого заряда и получаем один заряд положительный и один отрицательный, что в сумме дает нуль.
Таблица 1
Подобным же примером может служить другая частица, заряженная положительно, но отличная от протона. Она называется позитроном и представляет собой как бы зеркальное изображение электрона. Она во всех отношениях подобна электрону, за исключением того, что несет заряд противоположного знака и, что еще важнее, является античастицей, ибо, встретившись, электрон и позитрон взаимно уничтожаются и превращаются в свет. Так что сами по себе электроны не вечны. Электрон плюс позитрон дают свет. Этот свет, невидимый глазу, гамма-излучение; но видимый свет и гамма-излучение для физика – одно и то же, у них лишь разная длина волн. Таким образом, частица и соответствующая ей античастица могут взаимно уничтожаться, аннигилировать. Свет не имеет электрического заряда, но тут уничтожается один положительный и один отрицательный заряд, и суммарный заряд остается прежним. Таким образом, теория сохранения заряда немного усложняется, но по-прежнему имеет мало отношения к математике. Вы просто складываете число протонов с числом позитронов и отнимаете число электронов, а кроме того, учитываете другие частицы, например отрицательные антипротоны и положительные p+-мезоны, ибо каждая элементарная частица несет заряд (возможно, равный нулю). Нам надо лишь сложить все заряды и найти общий, и, что бы ни случилось потом, какая бы реакция ни произошла, он будет оставаться постоянным.
Это одна сторона закона сохранения заряда. Теперь возникает интересный вопрос. Достаточно ли сказать, что заряд просто сохраняется, или надо еще что-нибудь добавить? Если бы заряд представлял собой вещественную подвижную частицу и сохранялся благодаря этому, то сохранение было бы гораздо более конкретным свойством. Мыслимы два возможных способа сохранения заряда внутри ящика. Первый способ – заряд перемещается внутри ящика из одного места в другое. Другая возможность состоит в том, что заряд в одном месте исчезает и в то же самое мгновение возникает в другом месте; это происходит одновременно, и общий заряд по-прежнему остается постоянным. Вторая возможность сохранения отличается от первой, когда для исчезновения заряда в одном месте и появления его в другом что-то должно перемещаться в промежуточном пространстве. Первая форма сохранения называется локальным сохранением зарядов и несет в себе гораздо больше смысла, чем простое утверждение о неизменности полного заряда. Как видите, мы уточняем наш закон – если действительно заряд сохраняется локально. А это действительно так. Время от времени я пытался продемонстрировать вам возможности логики, позволяющей связывать одну идею с другой, и теперь хочу проследить с вами за рассуждениями Эйнштейна, который пришел к выводу, что если некоторая величина сохраняется (в данном случае речь пойдет о заряде), то она сохраняется локально. Это рассуждение основывается на следующем: если два человека пролетают мимо друг друга в космических кораблях, то вопрос о том, кто из них движется, а кто стоит на месте, нельзя решить путем эксперимента. Это так называемый принцип относительности; он гласит, что равномерное движение по прямой линии относительно. Для обоих наблюдателей любое физическое явление будет выглядеть одинаково и не скажет им, кто из них стоит и кто движется.
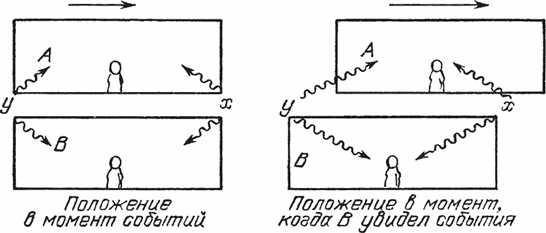
Рис. 18
Пусть у нас есть два космических корабля, А и B (рис. 18). Предположим, я придерживаюсь того мнения, что корабль B стоит, а корабль A движется мимо него. Запомните, что это только мое мнение. Вы можете стать на другую точку зрения, хотя и видите те же самые явления природы. Предположим теперь, что внутри корабля находится человек, который хочет выяснить, одновременно ли происходит исчезновение заряда в одном конце корабля и возникновение его в другом. Чтобы быть уверенным в одновременности этих событий, он не должен сидеть в носу корабля, иначе он увидит одно раньше другого, так как свет с кормы дойдет до него не сразу. Поэтому будем считать, что он поместился точно посредине корабля. Другой человек занимается такими же наблюдениями в своем корабле. Ударяет молния; в точке x создается заряд, и в тот же самый миг в другом конце корабля, в точке у, заряд уничтожается, исчезает. Заметьте, что это происходит одновременно, в полном соответствии с нашими представлениями о сохранении заряда. Если мы теряем электрон в одном месте, то находим электрон в другом, но из первого места во второе ничто не перемещается. Предположим, что исчезновение и возникновение зарядов сопровождается вспышками, которые служат нам сигналом. Человек B говорит, что оба события произошли одновременно, потому что он сидит посредине корабля, а свет от вспышки в x, где заряд создается, и от вспышки в у, где заряд уничтожается, приходит к нему одновременно. Человек B скажет: «Да, оба события произошли одновременно». Но как посмотрит на это человек с другого корабля? Он скажет: «Нет, друг мой, вы ошибаетесь. Я видел, что в x заряд возник раньше, чем исчез в у». А все это потому, что он движется в направлении x и свет от x до наблюдателя проделывает меньший путь, чем от у, и приходит раньше. Этот человек может утверждать: «Нет, сначала заряд возник в x, а уж затем исчез в у. Значит, какое-то время между возникновением заряда в x и исчезновением в у существовал дополнительный заряд. Тут нет никакого сохранения. Это противоречит закону». Тогда первый возразит: «Но вы же движетесь». А второй ответит: «А откуда вы знаете? Мне кажется, что это вы движетесь», и т. д. Если невозможно установить экспериментальным путем, движемся мы или находимся в покое, поскольку физические законы от этого не зависят, то из нелокальности закона сохранения следовало бы, что он будет казаться правильным только тем людям, которые стоят на месте в абсолютном смысле. Но, согласно принципу относительности Эйнштейна, такое состояние невозможно, а следовательно, закон сохранения заряда не может быть нелокальным. Локальность сохранения заряда созвучна теории относительности, и то же самое можно сказать обо всех остальных законах сохранения. Как выяснилось, этот принцип распространяется на все сохраняющиеся величины.
Заряд обладает еще одним очень интересным и удивительным свойством, которому до сих пор не найдено объяснения. Оно никак не связано с законом сохранения. Заряд всегда изменяется порциями. Если у нас есть заряженная частица, то заряд ее может быть равен единице или двум, минус единице или минус двум. Хотя это свойство не связано с сохранением, я должен записать в табл. 1, что заряд изменяется порциями. Очень удобно, что он изменяется порциями – благодаря этому нам легче усвоить теорию сохранения. Речь идет о вещах, которые можно пересчитать и которые перемещаются из одного места в другое. И наконец, еще одно важное свойство заряда: он является источником электрического и магнитного поля. Поэтому на практике несложно определить величину полного заряда электрическим путем. Заряд – это мера взаимодействия тела с электричеством, с электрическим полем. Поэтому мы должны внести в табл. 1 еще одно свойство заряда: он является источником поля; другими словами, электричество связано с зарядом. Таким образом, эта сохраняющаяся величина обладает двумя свойствами, не связанными непосредственно с сохранением, но тем не менее интересными. Первое: заряд изменяется порциями – и второе: он является источником поля.
Существует много законов сохранения, и мы рассмотрим еще несколько законов, подобных сохранению заряда в том смысле, что они сводятся к простому пересчету. Например, существует закон сохранения барионов. Нейтрон может превратиться в протон. Если каждый из них мы будем считать единицей, или барионом, то число барионов при этом не изменится. Нейтрон несет единичный барионный заряд, т. е. представляет собой один барион; протон – тоже один барион (мы только и делаем, что считаем да придумываем умные слова!), поэтому если происходит реакция, о которой я сейчас говорил, и нейтрон распадается на протон, электрон и антинейтрино, то полное число барионов не меняется. Но это не единственная реакция такого рода. Протон, взаимодействуя с другим протоном, может создавать множество странных вещей, например L-частицу, протон и K+-мезон (Λ и K+ – названия странных частиц):
(легко) p + p → Λ + p + K+.
В этой реакции участвуют два бариона, но получается как будто бы только один, поэтому либо Λ-частица, либо K+-мезон является барионом. Если мы проследим за поведением L-частицы, то обнаружим, что она очень медленно распадается на протон и p-мезон:
(медленно) Λ → p + π,
а p-мезон в конце концов распадается на электроны и еще кое-что. Здесь снова появляется барион – в протоне, поэтому мы считаем, что барионный заряд L-частицы равен единице, а K+-мезон не несет барионного заряда, его барионный заряд равен нулю.
Таким образом, в табл. 1 вдобавок к заряду появляется новая величина – барионный заряд, который мы подсчитываем по такому правилу: барионное число равно числу протонов плюс число нейтронов плюс число L-частиц минус число антипротонов минус число антинейтронов и т. д. Это просто правило счета. Величина сохраняется, изменяется порциями, и хотя никто не уверен, но каждому хочется думать по аналогии, что она является источником поля. Мы для того и составляем такие таблицы, чтобы попытаться угадать законы ядерных взаимодействий, и это один из быстрейших способов разгадать природу. Если заряд является источником поля, а барионный заряд во всех остальных отношениях ведет себя точно так же, то он тоже должен быть источником поля. К сожалению, опыт пока что не подтверждает нашей догадки; может быть, она и верна, но мы слишком мало знаем, чтобы утверждать это с полной уверенностью.
Можно назвать еще одно или два таких правила счета, например для лептонного заряда, но основная идея их та же, что и в случае барионов. Есть, правда, один закон, несколько отличающийся от других. Реакции странных частиц характеризуются скоростью их протекания: одни реакции происходят легко и быстро, другие – медленно и с трудом. Слова «легко» и «с трудом» я употребляю не в смысле практического осуществления экспериментов. Речь идет о том, насколько быстро протекают реакции в естественной обстановке. Имеется явственное различие между двумя типами реакций, которые я упомянул; взаимодействием пары протонов и гораздо более медленным распадом L-частицы. Оказывается, что если рассматривать только быстрые и легкие реакции, то существует еще одно правило счета, согласно которому L-частице соответствует минус единица, K+-мезону – плюс единица, а протону – нуль. Это число называется странностью или гиперонным зарядом. Оно сохраняется при всех быстрых реакциях, но не сохраняется при медленных. Поэтому в табл. 1 мы должны внести еще один закон сохранения, называемый законом сохранения странности или гиперонного заряда, – закон, справедливый только отчасти. Это очень странное свойство, и вполне понятно, почему сама величина названа странностью. Она сохраняется лишь в некоторых случаях, зато изменяется всегда порциями. При изучении сильных взаимодействий, с которыми связаны ядерные силы, физики обнаружили, что странность сохраняется. Это натолкнуло их на мысль, что при сильных взаимодействиях странность также является источником поля. Но опять-таки полной уверенности в этом нет. А рассказал я об этом для того, чтобы стало яснее, как законы сохранения помогают нам угадывать новые законы.
Время от времени выдвигались другие законы сохранения, той же природы, что и эти правила счета. Химики, например, когда-то думали, что при любой реакции число атомов натрия остается неизменным. Но атомы натрия не неизменны. Можно превратить атомы одного элемента в атомы другого, так что первый элемент полностью исчезнет. Когда-то считался справедливым и другой закон: что постоянна полная масса предмета. Это зависит от того, как вы определяете массу и принимаете ли вы во внимание энергию. Закон сохранения массы содержится в законе сохранения энергии, который мы сейчас разберем. Из всех законов сохранения этот закон самый трудный и абстрактный, но и самый полезный. Его труднее понять, чем те, о которых мы только что говорили, потому что в случае заряда и в других рассмотренных случаях механизм понятен – все сводится более или менее к сохранению каких-то предметов. Более или менее потому, что одни предметы превращаются в другие, но все же речь идет о простом пересчете.
Сохранение энергии – несколько более сложный вопрос, хотя и здесь у нас есть число, которое не меняется со временем, число это не соответствует никакому определенному предмету. Чтобы прояснить суть дела, я приведу вам следующее простенькое сравнение.
Вообразите, что мать оставляет в комнате ребенка с 28 кубиками, которые нельзя сломать. Ребенок играет с кубиками целый день, и мать, вернувшись, обнаруживает, что кубиков по-прежнему 28 – она следит за сохранением кубиков! Так продолжается день за днем, но однажды, вернувшись, она находит всего 27 кубиков. Оказывается, один кубик валяется за окном – ребенок его выкинул. Рассматривая законы сохранения, прежде всего нужно убедиться в том, что ваши предметы не вылетают за окно. Такая же неувязка получится, если в гости к ребенку придет другой мальчик со своими кубиками. Ясно, что все это нужно учитывать, рассуждая о законах сохранения. В один прекрасный день мать, пересчитывая, обнаруживает всего 25 кубиков и подозревает, что остальные 3 ребенок спрятал в коробку для игрушек. Тогда она говорит: «Я открою коробку». «Нет, – отвечает он, – не смей открывать мою коробку». Но мама очень сообразительна и рассуждает так: «Я знаю, что пустая коробка весит 50 г, а каждый кубик весит 100 г, поэтому мне надо просто-напросто взвесить коробку». Затем, подсчитав число кубиков, она получит
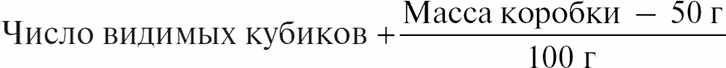
– опять 28. Какое-то время все идет гладко, но потом сумма опять не сходится. Тут она замечает, что в раковине изменился уровень грязной воды. Она знает, что если кубиков в воде нет, то глубина ее равна 15 см, а если положить туда один кубик, то уровень повысится на 0,5 см. Поэтому она добавляет еще одно слагаемое:
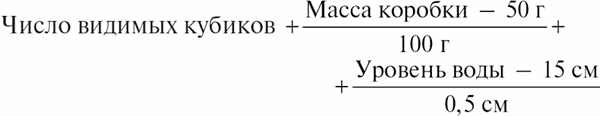
и снова получается 28. Ребенок становится все более изобретательным, а мать не уступает ему, добавляя все новые и новые слагаемые, которые соответствуют кубикам, но с математической точки зрения представляют собой абстрактные числа, потому что самих кубиков не видно.
Теперь я попытаюсь объяснить, в чем сходство между сохранением кубиков и сохранением энергии и в чем различие. Для начала предположим, что ни при каких условиях вы не можете видеть кубики. Слагаемое «число видимых кубиков» всегда отсутствует. Тогда мать будет складывать множество слагаемых, таких, как «кубики в коробке», «кубики в воде» и т. д. Кубиков энергии, насколько нам известно, вообще нет. Кроме того, в отличие от кубиков количество энергии не обязательно выражается целым числом. Бедная мамаша может получить в одном слагаемом 61/8 кубика, в другом – 7/8, в третьем – 21 кубик, что по-прежнему составляет в сумме 28. Так обстоит дело с энергией.
Мы установили, что для закона сохранения энергии у нас есть схема с целым набором правил. Согласно каждому из этих правил, мы можем вычислить значение для каждого из видов энергии. Если мы сложим все значения, соответствующие разным видам энергии, то сумма их всегда будет одинаковой. Но, насколько мы знаем, не существует никаких реальных частиц (кубиков или шариков) энергии. Это абстрактное, чисто математическое правило: существует число, которое не меняется, когда бы вы его ни подсчитали. Более вразумительного объяснения я дать вам не в силах.
Энергия существует во всевозможных формах, подобно кубикам в коробке, кубикам в раковине и т. д. Есть энергия, связанная с движением (кинетическая энергия); энергия, связанная с гравитационным взаимодействием (она называется потенциальной энергией тяготения); тепловая, электрическая и световая энергия; энергия упругости в пружинах; химическая энергия; ядерная энергия и, наконец, энергия, которой обладает частица в силу одного своего существования, – эта энергия прямо зависит от массы. Обнаружил ее, как вы знаете, Эйнштейн. Я имею в виду его знаменитое соотношение Е = тс².
Итак, существует много видов энергии, и мы кое-что знаем об их взаимосвязи, – в этом вопросе мы не совсем невежественны. Например, то, что мы называем тепловой энергией, в значительной степени лишь кинетическая энергия движения частиц в теле. Упругая энергия и химическая энергия имеют одинаковое происхождение – силы взаимодействия между атомами. Когда атомы перестраиваются в другом порядке, меняется энергия, а если меняется эта величина, то должна измениться и какая-то другая. Например, если вы что-то сжигаете, меняется химическая энергия, и вы обнаруживаете теплоту там, где ее раньше не было, ибо сумма энергий должна остаться прежней. Упругая энергия и химическая, обе связаны с взаимодействием атомов, и теперь нам известно, что эти взаимодействия являются комбинацией двух вещей – электрической энергии и опять-таки кинетической, только на этот раз формулу дает нам квантовая механика. Световая энергия – не что иное, как электромагнитная энергия, потому что свет теперь представляют себе как электрическую и магнитную волну. Ядерная энергия не выражается через другие виды энергии; сегодня я могу сказать только, что она – результат ядерных сил.
Закон сохранения энергии очень полезен в методическом отношении. Я приведу несколько простых примеров, чтобы показать вам, как, зная закон сохранения энергии и формулы для вычисления энергии, мы можем понять другие законы. Иными словами, многие другие законы не независимы, а являются как бы зашифрованными пересказами закона сохранения энергии. Простейший из них – правило рычага (рис. 19).
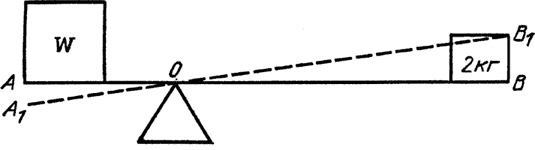
Рис. 19
На шарнире – рычаг. Длина одного плеча 1 м, другого – 4 м. Прежде всего вспомним закон для энергии тяготения: если у вас есть несколько грузов, то вы берете вес каждого груза, умножаете его на высоту над землей, складываете все вместе и получаете полную энергию тяготения. Пусть на длинном плече рычага груз массы 2 кг, на коротком – какой-то неизвестный груз массы Х; X – всегда неизвестная величина, поэтому давайте переименуем ее в W и сделаем вид, будто мы знаем о ней больше, чем на самом деле. Теперь вопрос в том, каким должен быть груз W для равновесия, чтобы рычаг тихо покачивался, но сильно не перекашивался. Если он тихо покачивается, то это означает, что энергия остается одинаковой и когда рычаг горизонтален, и когда он наклонен так, что груз в 2 кг поднялся, скажем, на 2 см. Раз энергия одинакова, рычагу безразлично, в каком он положении, и он не перекашивается. Если груз в 2 кг поднимается на 2 см, то насколько опускается груз W? Из рисунка ясно, что если AO = 1 м, а OB = 4 м, то при BB1 = 2 см отрезок AA1 будет равняться 0,5 см. Теперь применим закон для энергии тяготения. Вначале обе высоты BB1 и AA1 были равны нулю и общая энергия была равна нулю. Чтобы найти энергию повернувшегося рычага, мы умножаем вес груза массы 2 кг на высоту 2 см и складываем с неизвестным весом W, умноженным на высоту 0,5 см. Сумма должна дать прежнюю энергию – нуль. Поэтому
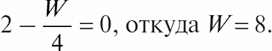
Это один из способов понять простой закон – хорошо известное вам правило рычага. Но интересно, что не только этот, но и сотни других законов можно тесно связать с различными видами энергии. Я привел вам этот пример только для того, чтобы показать, насколько полезен закон сохранения энергии.
Но вся беда в том, что на практике он не выполняется из-за трения в шарнире. Если что-то движется, например по горизонтальному полу катится шарик, то рано или поздно трение его остановит. А куда же денется кинетическая энергия шарика? Энергия движения шарика превратится в энергию колебания атомов пола и атомов шарика. Мир, если смотреть на него издали, кажется круглым, гладким, чисто отполированным шариком, но если посмотреть на него вблизи, он оказывается очень сложным: миллиарды крохотных атомов, всевозможные неровности. Он похож на крупную гальку у нас под ногами, ибо состоит из этих крохотных шариков. Таков и пол – бугристая дорога, насыпанная из шариков. Когда вы катите чудовищный голыш по этой гальке, вы видите, что галька – маленькие атомы – начинает подпрыгивать. После того как шар прокатился, атомы, которые остались позади, продолжают дрожать от тех толчков и ударов, которые они претерпели. Так в полу остается тепловая энергия, колебания атомов. На первый взгляд кажется, что закон сохранения несправедлив, ибо энергия прячется от нас и нам нужны термометры и другие приборы, чтобы ее обнаружить. Но как бы ни был сложен процесс, мы всегда находим, что энергия сохраняется, даже если не знаем других, более детальных законов.
Впервые закон сохранения энергии был продемонстрирован не физиком, а медиком. Он экспериментировал на крысах. Если вы сожжете пищу, то сможете найти, сколько выделилось тепла. Если такое же количество пищи вы дадите крысе, то пища вместе с кислородом превратится в углекислый газ, так же как и при горении. Измерив энергию в обоих случаях, вы обнаружите, что в живых существах происходит то же самое, что и в неживой природе. Жизнь так же подчиняется закону сохранения энергии, как и другие явления. Кстати говоря, всякий закон или принцип, справедливый для «неживой» природы и поддающийся проверке на великом феномене жизни, оказывается справедливым и там. В том, что касается законов физики, до сих пор не обнаружено разницы между неживыми предметами и живыми существами, хотя последние могут быть устроены гораздо сложнее.
Количество энергии в пище говорит вам, сколько тепла, механической работы и т. д. она может произвести. Измеряют эту величину в калориях. Когда говорят о калориях в пище, это не значит, что вы едите эти самые калории – они просто мера количества тепла, заключенного в пище. Физики иногда смотрят на других свысока и считают себя такими умными, что людям хочется поймать их на какой-нибудь ошибке. Я скажу вам, на чем их можно поймать. Им должно быть стыдно, что для измерения энергии они пользуются такой уймой способов и названий. Разве не бессмыслица, что энергию измеряют в калориях, в эргах, в электрон-вольтах, в килограммометрах, в британских тепловых единицах, в джоулях, в киловатт-часах – столько мер для одной и той же величины? Вы можете подумать, что по крайней мере современные первоклассные-то физики-теоретики приняли общую единицу, но загляните в их статьи: тут энергию измеряют и в кельвинах, и в мегагерцах, а теперь еще и в обратных ферми – последняя новинка. Если кому-нибудь нужны доказательства, что физики не лишены человеческих слабостей, то вот вам одно из них – столь огромное число единиц для измерения энергии.
Многие явления природы задают нам интересные загадки в связи с энергией. Не так давно были открыты объекты, названные квазарами. Они находятся на громадных расстояниях от нас и излучают в виде света и радиоволн так много энергии, что возникает вопрос, откуда она берется. Если энергия сохраняется, то состояние квазара после того, как он излучил такое чудовищное количество энергии, должно отличаться от первоначального. Вопрос в том, является ли источником энергии гравитация – не произошел ли гравитационный коллапс квазара, переход в иное гравитационное состояние? Или это мощное излучение вызвано ядерной энергией? Никто не знает. Вы скажете: «А может быть, закон сохранения энергии несправедлив?» Нет, когда явление исследовано так мало, как квазар (квазары настолько далеки, что астрономам нелегко их увидеть), и как будто бы противоречит основным законам, обычно оказывается, что не закон ошибочен, а просто мы недостаточно знаем явление.
Другой интересный пример использования закона сохранения энергии – реакция распада нейтрона на протон, электрон и антинейтрино. Сначала думали, что нейтрон превращается в протон и электрон. Но когда измерили энергию всех частиц, оказалось, что энергия протона и электрона меньше энергии нейтрона. Возможны были два объяснения. Во-первых, мог быть неправильным закон сохранения энергии. Бор предположил, что закон сохранения выполняется только в среднем, статистически. Но теперь выяснилось, что правильно другое объяснение: энергии не совпадают потому, что при реакциях возникает еще какая-то частица – частица, которую мы называем теперь антинейтрино. Антинейтрино уносит с собой часть энергии. Вы скажете, что антинейтрино, мол, только для того и придумали, чтобы спасти закон сохранения энергии. Но оно спасает и многие другие законы, например закон сохранения количества движения, а совсем недавно мы получили прямые доказательства, что нейтрино действительно существует.
Этот пример очень показателен. Почему же мы можем распространять наши законы на области, подробно не изученные? Почему мы так уверены, что какое-то новое явление подчиняется закону сохранения энергии, если проверяли закон только на известных явлениях? Время от времени вы читаете в журналах, что физики убедились в ошибочности одного из своих любимых законов. Так, может быть, не нужно говорить, что закон выполняется в тех областях, куда мы еще не заглядывали? Но если вы никогда не скажете, что закон выполняется там, куда вы еще не заглядывали, вы ничего не узнаете. Если вы принимаете только те законы, которые относятся уже к проделанным опытам, вы не сможете сделать никаких предсказаний. А ведь единственная польза от науки в том, что она позволяет заглядывать вперед, строить догадки. Поэтому мы вечно ходим, вытянув шею. А что касается энергии, она, вероятнее всего, сохраняется и в других местах.
Вот почему наука недостоверна. Как только вы скажете что-нибудь об области опыта, с которой непосредственно не соприкасались, вы сразу же лишаетесь уверенности. Но мы обязательно должны говорить о тех областях, которых никогда не видели, иначе от науки не будет проку. Например, при движении тела его масса меняется из-за сохранения энергии. Из-за эквивалентности массы и энергии энергия, связанная с движением, проявляется как дополнительная масса. Двигаясь, тела становятся тяжелее. Ньютон был другого мнения. Он считал, что массы постоянны. Когда обнаружилось, что представления Ньютона неверны, все говорили: «Это ужасно! Физики нашли у себя ошибку! Почему же они думали, что они правы?» Эффект этот очень мал и проявляется только при скоростях, близких к скорости света. Если вы запустите волчок, то масса его останется такой же, как и в спокойном состоянии, с точностью до ничтожной дроби. Но тогда они должны были бы говорить так: «Если скорость не превышает такого-то значения, масса волчка не меняется». Все было бы ясно, не правда ли? Но нет. Ведь опыты проводились только с деревянными, медными и стальными волчками, и пришлось бы говорить: «Когда волчки, сделанные из меди, дерева и стали, крутятся не быстрее, чем с такой-то скоростью…» Как видите, мы не знаем всех условий, необходимых для опыта. Неизвестно, будет ли сохраняться масса радиоактивного волчка. Поэтому, если мы хотим, чтобы от науки была какая-то польза, мы должны строить догадки. Чтобы наука не превратилась в простые протоколы проделанных экспериментов, мы должны выдвигать законы, простирающиеся на еще не изведанные области. Ничего дурного тут нет, только наука оказывается из-за этого недостоверной. А если вы думали, что наука достоверна, вы ошибались.
Итак, возвращаясь к нашему списку законов сохранения (см. табл. 1), мы можем внести туда энергию. Насколько нам известно, она сохраняется в точности. Элементарной единицы энергии не существует. Далее, является ли она источником поля? Да. Эйнштейн считал, что гравитация порождается энергией. Энергия эквивалентна массе, и, следовательно, мысль Ньютона, что гравитация порождается массой, трансформировалась в утверждение, что гравитацию производит энергия.
Существуют другие сохраняющиеся величины, подобные энергии в том смысле, что они являются числами. Одна из них – количество движения. Если взять все массы системы, перемножить их на скорости и сложить, то сумма будет количеством движения системы; полное количество движения системы сохраняется. Согласно нынешним представлениям энергия и количество движения тесно связаны, поэтому я поместил их в одном столбце.
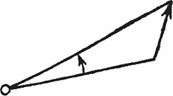
Рис. 20
Еще пример сохраняющейся величины – момент количества движения, о котором мы уже говорили. Например, если у нас есть движущееся тело и мы выберем произвольный центр, то скорость увеличения площади (рис. 20), описываемая отрезком, соединяющим тело с центром, умноженная на массу тела, называется моментом количества движения. Таким образом, момент количества движения численно равен площади, описываемой отрезком, соединяющим тело с центром, при движении тела за единицу времени. Сложив моменты всех тел, входящих в систему, мы получим момент количества движения системы. Эта величина не меняется. Итак, мы имеем сохранение момента количества движения. Кстати, многим часто кажется, будто момент количества движения не сохраняется. Подобно энергии, он проявляется в различных формах. Большинство людей думают, будто он связан только с движением, но я покажу вам, что он проявляется и в других формах. Если в проволочную катушку вдвигать магнит, то магнитное поле, магнитный поток внутри ее, увеличится и по проводу пойдет электрический ток. Вообразите, что вместо провода – диск, в котором имеются электрические заряды наподобие электронов в проволоке (рис. 21). Теперь я пододвигаю издалека магнит, вдвигаю очень быстро вдоль оси, точно в середину, и магнитный поток изменяется. Так же как и в проволоке, магнитные заряды начинают двигаться по кругу, и, если диск насажен на подшипник, он закрутится. Это не похоже на сохранение момента: когда магнит далеко от диска, диск не поворачивается, а когда близко – диск крутится. Мы получили вращение задаром, а это против правил. «Ах так, – скажете вы, – значит, должно существовать какое-то другое взаимодействие, заставляющее магнит крутиться в обратную сторону». Ничего похожего. На магнит не действует электрическая сила, которая стремилась бы повернуть его в обратную сторону. Все объясняется тем, что момент проявляется в двух формах. Одна из них – момент, связанный с движением, а другая – момент, связанный с электрическим и магнитным полями. Вокруг магнита существует поле со своим моментом, который не проявляется в движении, но по знаку противоположен вращению. Если мы проделаем опыт в обратном порядке (рис. 22), это станет еще яснее. Когда диск с заряженными частицами и магнит находятся рядом и оба неподвижны, я говорю, что поле обладает моментом, моментом в скрытой форме, не проявляющимся в механическом вращении. Когда же вы убираете магнит, поля разъединяются, и момент количества движения должен теперь проявиться – диск закрутится. Причина, заставляющая его крутиться, – это явление электромагнитной индукции.
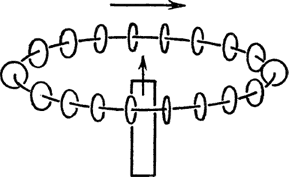
Рис. 21
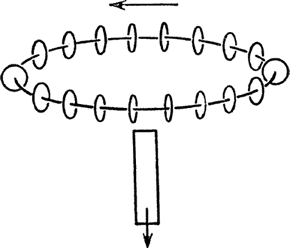
Рис. 22
Меняется ли момент количества движения порциями, я затрудняюсь сказать. На первый взгляд он никак не может изменяться порциями, ибо зависит от того, под каким углом вы строите проекцию системы. Вы смотрите на изменяющуюся площадь и, естественно, видите ее по-разному в зависимости от того, смотрите ли вы на нее прямо или под углом. Если момент изменяется порциями и, глядя на систему под одним углом, вы нашли, что он равен 8 единицам, а потом чуть-чуть изменили угол, то число единиц изменится незначительно, скажем, станет чуть-чуть меньше 8. Но 7 не чуть-чуть меньше 8; 7 меньше 8 на вполне определенную величину, так что момент вряд ли может изменяться порциями. Однако тонкости и странности квантовой механики позволяют обойти это доказательство: если мы измерим момент количества движения относительно любой оси, он, как ни странно, всегда будет выражаться целым числом единиц. Правда, в отличие от электрического заряда, это не те единицы, которые можно подсчитать. Момент изменяется порциями в математическом смысле таким образом, что при любом измерении величина его выражается целым числом. Но мы не можем толковать его так же, как целое число единичных электрических зарядов – воображаемых единиц, которые мы можем пересчитать: одна, другая, третья… В случае момента количества движения мы не можем представить их себе как отдельные единицы, и тем не менее число их – всегда целое… Что крайне странно.
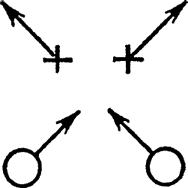
Рис. 23
Есть и другие законы сохранения. Они не так интересны, как те, о которых я рассказывал, и речь в них идет не о сохранении величины. Предположим, у нас есть устройство, в котором частицы движутся симметрично. Пусть их движениям свойственна двусторонняя симметрия (рис. 23). Тогда, согласно законам физики, при любых перемещениях и столкновениях вы можете ожидать, и ожидать не напрасно, что, взглянув на эту систему позже, вы обнаружите в ней прежнюю симметрию. Следовательно, существует еще один вид сохранения – сохранение характера симметричности. Полагалось бы и этот закон занести в нашу таблицу, но тут не сохраняется никакая определенная величина, поддающаяся измерению. О законе сохранения симметрии мы поговорим подробнее в следующей лекции. Классическую физику он мало интересует потому, что такие красивые симметрические начальные условия там очень редки и практического значения он почти не имеет. В квантовой же механике, где мы имеем дело с очень простыми системами вроде атомов, их внутреннее строение часто бывает симметричным (например, с двусторонней симметрией) и характер симметрии сохраняется. Вот почему этот закон важен для понимания квантовых явлений.
Еще один интересный вопрос: заложен ли более фундаментальный принцип в законах сохранения или мы должны принимать их такими, как они есть? Этот вопрос я отложу до следующей лекции, но одну его сторону хочу отметить сразу. При популярном изложении этих разнообразных принципов они кажутся взаимно не связанными. Зато при более глубоком понимании вы обнаруживаете между ними тесную связь – каждый из них так или иначе подразумевает в себе остальные. Взять хотя бы связь между относительностью и локальным характером сохранения. Если бы я не пояснил эту связь примером, то могло бы показаться чудом, что из невозможности определить, как быстро вы движетесь, вытекает, что сохраняющаяся величина не может исчезнуть в одном месте и одновременно возникнуть в другом.

Рис. 24
Теперь я хотел бы показать вам, какова связь между сохранением момента количества движения, сохранением количества движения и сохранением некоторых других величин. При сохранении момента количества движения мы имеем дело с площадью, описываемой движущимися частицами. Если нам дано несколько частиц (рис. 24) и мы примем за центр очень далекую точку x, то расстояния до всех частиц будут почти одинаковы. В этом случае при вычислении площадей, или моментов количества движения, нужно учитывать только одно – составляющую скорости, которая на рис. 24 вертикальна. Мы обнаружим, что сумма всех масс, умноженных на их вертикальные скорости, постоянна, ибо постоянен момент количества движения относительно любой точки, и если точка выбрана достаточно далекая, то момент зависит лишь от масс и скоростей. Таким образом, из сохранения момента количества движения вытекает сохранение количества движения. А оно, в свою очередь, подразумевает сохранение еще одной величины, настолько связанной с количеством движения, что я даже не стал вносить ее в табл. 1. Я имею в виду положение центра масс (рис. 25).
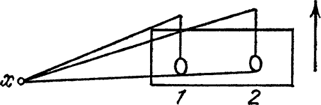
Рис. 25
Масса в ящике не может переместиться из одного положения в другое просто так, сама по себе. Сохранение массы тут ни при чем: масса все время одна и та же, речь идет лишь о ее перемещениях. Заряд мог бы переместиться, а масса – нет. Позвольте объяснить почему.
Предположив, что ящик плавно идет вверх, найдем момент количества движения относительно не очень далекой точки х. Если при движении ящика вверх масса находится в положении 1, то площадь, описанная ее радиусом, будет изменяться с определенной скоростью. Если масса передвинется в положение 2, то площадь станет увеличиваться быстрее: высота будет прежней, потому что ящик поднимается с прежней скоростью, а расстояние от х до массы увеличилось. Но, согласно закону сохранения момента, быстрота изменения площади не может изменяться. Поэтому масса не имеет права передвинуться сама по себе: вы должны что-то подтолкнуть или еще как-нибудь увеличить момент количества движения. Вот почему ракета не может двигаться в пустоте, но движется. Если у вас несколько масс и одна двинулась вперед, то другие вынуждены двигаться назад – так, чтобы перемещения вперед и назад взаимно уравновесились. Так работает ракета. Сначала она, скажем, неподвижно висит в пустоте, потом выбрасывает газ назад и из-за этого летит вперед. Главное – что все вещество, центр массы, масса в среднем остаются на прежнем месте. Нужная часть полетела вперед, а ненужная, нас не интересующая, отброшена назад. Теорем о сохранении только нужных вещей нет, они говорят лишь о сохранении всего в целом.
Поиски законов физики – это вроде детской игры в кубики, из которых нужно собрать целую картинку. У нас огромное множество кубиков, и с каждым днем их становится все больше. Многие валяются в стороне и как будто бы не подходят к остальным. Откуда мы знаем, что все они из одного набора? Откуда мы знаем, что вместе они должны составить цельную картинку? Полной уверенности нет, и это нас несколько беспокоит. Но то, что у многих кубиков есть нечто общее, вселяет надежду. На всех нарисовано голубое небо, все сделаны из дерева одного сорта. Все физические законы подчинены одним и тем же законам сохранения.

