Перескакивающие электроны – спектры
В 1849 году Иоганн Бальмер (1825–1898) защитил докторскую диссертацию в Базельском университете, Швейцария. Он прожил в Базеле всю свою жизнь, работая учителем в женской школе и читая лекции в университете. Бальмер, любитель нумерологии, считал, что практически все (и число овец в стаде, и число ступенек на египетской пирамиде, и т. д.) в этой жизни имеет что-то вроде особенной связи с числами и формулами. Хоть Бальмер был по образованию математик, он не внес значительного вклада в свою область, но оказал содействие дальнейшему развитию физики своей спектральной формулой для атома водорода.
Его достижение было по-настоящему выдающимся. В то время Бальмер знал только о четырех частотах в спектре атома водорода, которые экспериментально определил Андерс Ангстрем (1814–1874). Используя только эти четыре значения, Бальмер в шестьдесят лет составил формулу, предсказавшую полный спектр частот атома водорода (а также верно предсказавшую нижнюю и верхнюю границы диапазона частот). Вскоре после этого Бальмер узнал, что эта формула не только объяснила те четыре изначальных значения, но и правильно предсказала двенадцать других частот.
В 1885 году он опубликовал свои труды в двух статьях, которые сделали его имя бессмертным. За годы было определено еще больше спектральных частот, но формула Бальмера остается неизменной. В 1890 году Йоханнес Ридберг (1854–1919) обнаружил, что формула Бальмера на самом деле является частным случаем более общей формулы (которую сейчас мы называем формулой Ридберга):
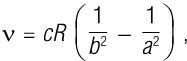
где ν – частота, c – скорость света, а R – постоянная Ридберга. Частоты Бальмера для атома водорода можно получить, если установить b = 2 и a = 3, 4, 5, 6 и т. д. Хотя эта формула правильно предсказала линии, наблюдаемые в спектре атома водорода, никто не знал, почему она работала – она просто работала. В течение еще тридцати лет атом держал это в тайне.
Следуя предложению Хансена, Бор взглянул на формулу Бальмера. Возможно, он увидел ее в общем варианте Ридберга (см. выше). Формула была хорошо известна, и, скорее всего, Бор увидел ее еще студентом, только чтобы потом забыть. Мы уже обсуждали то, как Бор предположил, что энергия связи электрона в атоме квантована подобно тому, как Планк проквантовал энергию резонаторов. Используя эту гипотезу с некоторой очень простой классической физикой, Бор смог получить общее выражение для разности энергий связи ΔE двух квантовых состояний с квантовыми числами n1 и n2:
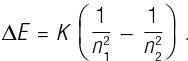
Снова увидев формулу Бальмера, Бор, должно быть, немедленно понял, как вытащить физику, все эти годы глубоко скрывавшуюся в этой формуле. А затем Бор выдвинул следующую гипотезу: что разность энергий квантовых состояний электрона равна энергии светового кванта Эйнштейна, hν:
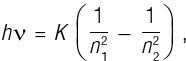
таким образом получив формулу Бальмера, где R = K / hc. На самом деле Бор смог посчитать постоянную Ридберга и обнаружить, что она отлично согласуется с экспериментальным значением. Более того, числа a и b из формулы Бальмера тождественны квантовым числам n1 и n2, нумерующим квантовые состояния, а не являются просто какими-то целыми числами без физического смысла. Таким образом, новый вариант теории Бора получил неоценимую поддержку. Давайте посмотрим поближе на физическое понимание, лежащее за выводом Бора.
К тому времени, когда Бор познакомился с теорией Бальмера, у него уже было то, что нужно, чтобы вывести выражения для энергии связи ΔE. Однако, вероятнее всего, именно взгляд на формулу Бальмера заставил Бора завершить это преобразование. Теперь оставался только один шаг, чтобы его закончить. Бору нужно было приравнять разность энергий связи к энергии одного фотона, рассчитываемой в соответствии с формулой Эйнштейна для световых квантов, приходя к выражению:
ΔE = hν,
известному как правило частот Бора.
Математика этого шага очевидна (просто приравнять ΔE к hν), но физическая интерпретация Бора поразительна. Согласно Бору, электрон может менять квантовое состояние «перескакиванием» из одного в другое. Если электрон переходит из квантового состояния с большей энергией в состояние с меньшей, он испустит один фотон, который появится в спектре частот атома. Другими словами, частотный спектр атома возникает вследствие «перескоков» всех возбужденных электронов из состояний с большими энергиями в состояния с меньшими, при которых они излучают фотоны. Поглощение одного фотона приводит к тому, что электрон переходит из состояния с меньшей энергией в состояние в большей. Нужно осознать, что для двух заданных квантовых состояний энергия, или частота фотона, излученного при «перескоке» электрона «вниз», равна энергии, или частоте, поглощенного фотона при «перескоке» электрона «вверх». Получается, что более чем через пятьдесят лет после Кирхгофа модель Бора окончательно объяснила выводы, которые он сделал из опытов с веществом: как и атом, оно будет излучать и поглощать на той же самой частоте.
Другим успехом теории Бора было правильное предсказание серии Пикеринга. В 1896 году Эдуард Чарльз Пикеринг (1846–1919) обнаружил в свете звезд серию спектральных линий, которую он приписал водороду. Проблема была в том, что формула Бальмера не предсказывала эти линии. Примерно в то же время, когда Бор составлял свою теорию, интерес к серии Пикеринга вновь появился в работе Альфреда Фаулера (1868–1940), обнаружившего спектральные линии в лабораторном эксперименте. Используя свою теорию, Бор смог правильно объяснить эту серию линий, приписав их к частотному спектру однократно ионизованного гелия.
В однократно ионизованном состоянии атом гелия очень «водородоподобный» в том смысле, что у него, как у водорода, имеется только один электрон. От атома водорода он отличается ядром, содержащим два протона (а в ядре атома водорода – только один) и два нейтрона (тогда как в атоме водорода их нет). Это был другой крупный успех теории Бора. Сначала Эйнштейн отвечал на нее слабой похвалой, но, когда он узнал, что она смогла правильно предсказать серию Пикеринга, он сменил тон: «Это громадное достижение. Тогда теория Бора, несомненно, верна».
Были и другие успехи. Используя свою теорию, Бор сделал правильный вывод, что рентгеновское излучение возникает при переходе внутреннего электрона на орбиталь, или квантовое состояние, с меньшей энергией, оставшейся вакантной из-за того, что находившейся там другой электрон был прежде выбит из атома. Более того, Бор предпринял первый шаг навстречу квантовой химии, выяснив, что химические свойства атомов обусловливаются их внешними, или валентными, электронами.
В 1913 году статью Бора об атоме водорода опубликовали, и за ней тут же последовали две другие. Отношение к его теории было неоднозначным. Возможно, один из самых беспокоящих вопросов к теории задал Резерфорд, удивлявшийся тому, каким образом электрон, находящийся в каком-то квантовом состоянии, «решает», в какое состояние перейти дальше. Проблема состояла в том, что, казалось, в теории отсутствовала типичная идея причины и следствия (причинности). В самом деле, эта проблема, присущая квантовой механике, возникла снова позже, когда Эйнштейн вернулся к взаимодействию света и вещества.

