Фотоэлектрический эффект
По иронии судьбы в том же самом наборе экспериментов, которые проводил Герц для исследования волновой природы света, описанной теорией Максвелла, он также случайно обнаружил фотоэлектрический эффект. Это явление было небольшим бременем для достопочтенной максвелловской теории света. Когда освещают определенные типы металлов, с поверхности испускаются, то есть выбиваются и становятся свободными, электроны (см. рис. 14.1). Это явление называется фотоэлектрическим эффектом, и с помощью теории Максвелла невозможно было объяснить несколько его особенностей:
• Чтобы электроны были выбиты и стали свободными, частота света, попадающего на поверхность (падающего света), должна быть больше определенного значения, которое является характеристикой металла, освещаемого им. Другими словами, имеется граничная частота, и частота падающего света должна быть выше нее, иначе фотоэлектрического эффекта не будет. Это не согласуется с волновой теорией света, которая предсказывает, что электроны будут вылетать при любой частоте падающего света, если его интенсивность достаточно велика.
• Как только частота света превышает граничное значение, электроны начинают вылетать с определенной скоростью, или кинетической энергией. В то время как число вылетающих электронов пропорционально интенсивности света, кинетическая энергия, или скорость, с которой они вылетают, нет. На самом деле их кинетическая энергия определяется частотой света, а не его интенсивностью.
• Электроны вылетают почти сразу после того, как их выбивает свет. То есть эффект почти мгновенный. Это происходит даже при низкой интенсивности света.
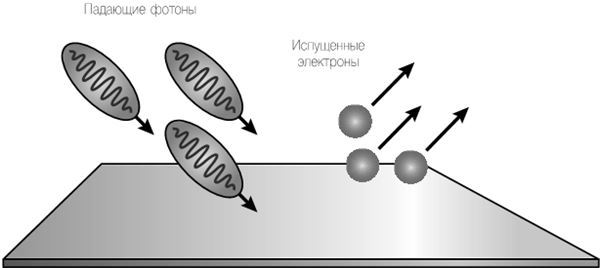
Рис. 14.1. Приходящие (падающие) фотоны энергии hν попадают на поверхность металла. Так они выбивают электроны, и те освобождаются от притяжения со стороны металла.
Эйнштейн ясно видел решение всех этих трудностей. Как мы обсуждали раньше, он предположил, что свет состоит из квантов. Другими словами, свет состоит из частиц с энергией hν у каждой, которые мы сегодня называем фотонами. Таким образом, когда свет облучает металл, фотон может столкнуться с электроном и передать ему свою энергию hν. Эта передача энергии почти мгновенна, поскольку энергия фотона не распределена по большому объему, а сконцентрирована, поэтому передача столь быстра. Итак, когда фотон ударит по электрону, последний улетит за пределы металла, только если энергия фотона «достаточна». Что мы понимаем под достаточностью?
Притяжение между электроном и атомом, с которым он связан, удерживает отдельный электрон в металле; положительно заряженное ядро атома удерживает отрицательно заряженный электрон и не дает ему просто так улететь от него. Поэтому фотону нужно иметь достаточную энергию, чтобы освободить электрон от этой силы притяжения. Это минимально необходимое количество энергии – всего, что меньше, будет недостаточно для освобождения электрона. Это объясняет вышеупомянутую граничную частоту.
У фотона должна быть определенная частота ν, то есть определенное количество энергии hν (поскольку h – это постоянная), чтобы он мог освободить электрон из тисков атома. Минимальное количество энергии называется работой выхода W – работой, которую нужно произвести, чтобы электрон освободился, – и она является неотъемлемым свойством металла. Более того, она объясняет, почему фотоэлектрический эффект наблюдают только при свете с частотой выше определенной, а не при любой, если интенсивность достаточно велика, как это предсказывается в волновой теории.
Согласно фотонной концепции, чем больше интенсивность, тем больше фотонов с одинаковой энергией. Пусть даже у нас больше фотонов, если у них нет минимальной энергии (работы выхода W), требуемой для освобождения электрона от атома, то ничего не произойдет. А что если энергия больше, чем работа выхода? Что случится с оставшейся энергией? В конце концов, нам известно, что она не исчезает просто так, поскольку, как мы узнали из части 1, энергия сохраняется.
Оставшаяся энергия уходит на сообщение скорости электрону, с которой он улетает. Чем больше энергии остается, тем больше будет скорость электрона при его вылете из металла. На самом деле, чтобы электрон улетел, нужно немного больше энергии, чем просто работа выхода. Как упомянуто, бо2льшая интенсивность означает больше фотонов, и больше фотонов с «достаточной» энергией приведут к тому, что больше электронов вылетят из металла.
Другими словами, при достижении граничной частоты увеличение интенсивности непосредственно увеличит число электронов, покидающих металл. Однако она не повлияет на скорость, с которой они улетают; на нее влияет лишь частота фотона, ударяющего по электрону. Вспомним, что скорость является результатом «оставшейся энергии», о которой мы говорили выше. Сумма того количества энергии и работы выхода W равна количеству энергии, которую имеет фотон, hν, и которая зависит только от частоты ν фотона. Мы можем суммировать все эти результаты в простом уравнении, впервые написанном Эйнштейном:
hν = Kmax + W,
где Kmax – максимальная кинетическая энергия, которую может приобрести электрон. Ясно, что это просто уравнение для закона сохранения энергии, подобное тому, о котором мы говорили в части 1, с тем единственным отличием, что сейчас мы говорим о сохранении энергии микроскопических частиц – даже они сохраняют энергию.
Световые кванты Эйнштейна и уравнение сохранения энергии успешно объяснили фотоэлектрический эффект и другие явления которые волновая теория света и теория Максвелла объяснить не смогли. Вы, наверно, воображаете, что физическое сообщество встретило такой прорыв с распростертыми объятиями. К сожалению, нет.

