Книга: Тайна за тремя стенами. Пифагор. Теорема Пифагора
Назад: ГЛАВА 1 Правда и миф о Пифагоре
Дальше: ГЛАВА З Пифагорейское братство
ГЛАВА 2
Теорема
Теорема Пифагора — одно из самых значительных математических достижений в истории. И хотя ее приписывают самосскому мудрецу, известно, что схожие результаты были получены еще в древних цивилизациях Востока. Однако мы не можем отказывать греческим геометрам в гениальности: переход от частного к общему, от наблюдения к теореме — это их заслуга.
Насколько в общественном сознании фигура Пифагора ассоциируется с математикой, настолько же она связана с теоремой, носящей его имя. Однако ее точная формулировка известна меньше, хотя данную теорему изучают в школах по всему миру, и еще меньше люди понимают, зачем в действительности она нужна.
На вопрос о пользе теоремы ответить несложно. Она решает классическую проблему геометрии большой теоретической важности. Таким образом, не говоря о практической пользе, важность ее состоит в том, что она служит основой множества теорем в тригонометрии и аналитической геометрии и, очевидно, в том, что она необходима для извлечения квадратных корней. Как мы увидим далее, проблема извлечения корней из чисел проявляется в достаточно простых математических задачах, таких как вычисление длины диагонали квадрата или прямоугольника по его сторонам.
Возможно, своим влиянием и известностью эта теорема обязана ощущению неочевидности, которое остается после ее анализа. В отличие от других теорем, в этой нет ничего интуитивно понятного, что объясняло бы ее свойства, которые мы сейчас еще раз рассмотрим, так что ее понимание — это акт чисто логической дедукции. Именно поэтому некоторые считают теорему квинтэссенцией математики.
КАТЕТЫ, ГИПОТЕНУЗА И УГЛЫ
Катеты — это стороны, прилегающие к прямому углу прямоугольного треугольника, а гипотенуза — сторона, противоположная прямому углу. Термины эти пришли к нам из греческого языка. Слово «катет» восходит к древнегреческому kathetos, что значит «прямостоящий, перпендикулярный», а «гипотенуза» происходит от hypoteinousa — «натянутая, стягивающая». Это определение обозначает, что гипотенуза представляет собой диаметр окружности, на которой лежит вершина прямого угла прямоугольного треугольника, то есть диаметр, который «стягивает» прямой угол. Поскольку речь идет об углах, возможно, источник этих терминов — наблюдения над положениями мышц ноги или плеча и предплечья.
ОПРЕДЕЛЕНИЕ ТЕОРЕМЫ
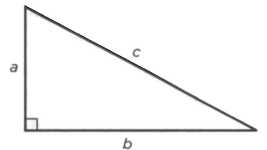
Самое значительное открытие, которое традиция приписывает Пифагору, — это описание прямоугольного треугольника, устанавливающее соотношение между его катетами и гипотенузой. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов длин двух других сторон треугольника (см. рисунок 1). Определение теоремы звучит как «сумма квадратов катетов равна квадрату гипотенузы», а ее алгебраическое выражение выглядит так:
a2 + b2 = c2.
Эту теорему можно сформулировать и более строгим образом, следуя современным математическим нормам. Ее определение в специальных геометрических терминах выражается следующим образом (см. рисунок 2):
Дан треугольник ABC; угол С прямой (то есть треугольник является прямоугольным), если площадь квадрата, построенного на стороне с, противоположной углу С, равна сумме площадей квадратов, построенных на двух других сторонах a и b: a2 + b2 = c2.
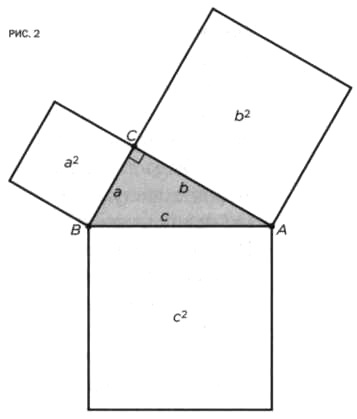
Из уравнения а2 + b2 = с2 следует, что
а = √(с2-b2),
b = √(с2-а2),
c = √(a2 + b2).
Во времена Пифагора эта теорема служила для определения перпендикулярности. Ведь в прямоугольном треугольнике «квадрат гипотенузы равен сумме квадратов катетов», потому что катеты перпендикулярны друг другу. С другой стороны, если на практике соотношение сторон именно таково (а2 + b2 = с2), отсюда можно вывести, что данный треугольник — прямоугольный.
В наши дни угольник и копировальная бумага, которые применяются для построения технических чертежей, позволяют проводить не только перпендикулярные отрезки, но и комбинировать углы их пересечения из углов в 30°, 45°, 60° и 90°. В современном мире при черчении с применением плотницкого или столярного угольника тем же инструментом можно проверять перпендикулярность линий. А в Древней Греции архитектор, желающий проверить, перпендикулярны ли друг другу стены, мог использовать теорему Пифагора. Инструментом для измерения длины в то время служила веревка с завязанными на равных расстояниях узелками. Этой веревкой архитектор отмерял 3 единицы по одной стене и 4 по другой, после чего он мог определить, что стены перпендикулярны друг другу, если между двумя этими отметками укладывалось 5 единиц (52 = З2 + 42). Так проблема измерения углов сводилась к проверке соотношения длин, то есть гораздо более простой операции.
ПРЕДШЕСТВЕННИКИ ТЕОРЕМЫ ПИФАГОРА
Египтяне и вавилоняне уже знали, что треугольник с соотношением сторон 3:4:5 прямоугольный, но, видимо, только греки заметили, что З2 + 42 = 52 и, таким образом, первыми сформулировали теорему в ее общем виде. Тысячелетние китайская и индийская культуры тоже довольно рано обратили внимание на эту геометрическую особенность — проблема диагонали квадрата была известна в этих культурах, а вот в великих цивилизациях доколумбовой Америки или Африканского континента (за исключением Египта) она не ставилась. В любом случае, Пифагору или кому-то из его учеников принадлежит заслуга открытия того, что описанное выше соотношение справедливо для всех возможных прямоугольных треугольников.
ПРЕДШЕСТВЕННИКИ ТЕОРЕМЫ ПИФАГОРА
Задолго до того как Пифагор сформулировал общий закон, касающийся всех прямоугольных треугольников, в Вавилоне эпохи Хаммурапи — властителя, умершего примерно в 1750 году до н. э., — уже знали, как высчитывать «пифагоровы тройки», то есть такие комбинации положительных чисел (a, b, с), при которых а2 + b2 = с2. Вот некоторые примеры: (3, 4, 5), (5, 12, 13) и (8, 15, 17). Согласно теореме Пифагора, каждая из этих троек представляет собой длины сторон прямоугольного треугольника.
Наш главный источник информации о Вавилоне и Месопотамии — знаменитые глиняные клинописные таблички, на которых писали, пока глина была еще мягкой, а затем обжигали их в печи или высушивали на солнце, что придавало им достаточную твердость. Из всех этих табличек особую ценность для истории математики представляют те, что написаны около 2000 года до н.э. В самых древних записях использовался аккадский язык. Слова в нем состоят из одного или более слогов, и каждое из них отображается группой прямых черточек. Для письма аккадцы использовали палочку с треугольным концом, который они наклонно вдавливали в табличку, от чего оставались клиновидные следы, ориентированные в разных направлениях, поэтому такое письмо называется клинописью.
Среди 300 вавилонских табличек математического содержания из полумиллиона найденных до сегодняшнего дня особый интерес представляет табличка, называемая Плимптон 322 (табличка № 332 из коллекции издателя Джорджа Артура Плимптона, которую он в 1932 году передал Колумбийскому университету). Эта табличка относится к древнему периоду династии Хаммурапи (который охватывает эпоху между 1800 и 1600 годами до н.э.) и на ней изображена таблица с четырьмя колонками символов, которые, по-видимому, представляют числа, записанные в вавилонской шестидесятеричной системе.
Эти ряды чисел можно принять за записи торговых счетов, но при их внимательном изучении было сделано выдающееся открытие: это список пифагоровых троек по формуле а2 + b2 = с2. Таким образом, табличка Плимптона доказывает, что вавилоняне знали элементарную геометрию и начала алгебры.
Как вавилоняне нашли эти пифагоровы тройки? Почему они их интересовали? Для составления этой таблицы они, возможно, использовали известный им алгоритм, который оставался в забвении следующие 1500 лет, до Евклида с его «Началами».
| I. | II.b | III.d | IV. | l |
| (1) 59 00 15 | 159 | 2 49 | 1 | 2 00 |
| (1) 56 56 58 14 50 06 15 | 56 07 | 3121 [1 20 25] | 2 | 57 36 |
| (1) 55 07 4115 33 45 | 116 41 | 150 49 | 3 | 120 00 |
| (1) 53 10 29 32 52 16 | 3 3149 | 5 09 01 | 4 | 3 45 00 |
| (1)48 54 0140 | 105 | 137 | 5 | 112 |
| (1) 47 06 4140 | 519 | 8 01 | 6 | 600 |
| (1) 43 11 56 28 26 40 | 38 11 | 59 01 | 7 | 45 00 |
| (1) 41 33 59 03 45 | 1319 | 20 49 | 8 | 16 00 |
| (1) 38 33 36 36 | 901 [801] | 12 49 | 9 | 10 |
| (1) 35 10 02 28 27 24 26 40 | 122 41 | 216 01 | 10 | 148 00 |
| (1) 33 45 | 45 | 115 | 11 | 100 |
| (1) 29 21 54 02 15 | 27 59 | 48 49 | 12 | 40 00 |
| (1) 27 00 03 45 | 7121 [2 41] | 4 49 | 13 | 4 00 |
| (1) 25 48 5135 06 40 | 29 31 | 53 49 | 14 | 45 00 |
| (1) 23 13 46 40 | 56 | 53 [146] | 15 | 130 |
На следующей странице в таблице показаны 15 из 38 пифагоровых троек из этой таблички. Хотя клинописные символы заменены на привычные цифры, для понимания таблицы нужно сделать несколько уточнений. Четвертая колонка содержит номер строки. Вторая и третья колонки показывают значение гипотенузы и катета прямоугольного треугольника, записанные в шестидесятеричной системе. В последней колонке, обозначенной буквой «l», находятся значения второго катета. Содержимое первой колонки вызывает некоторое удивление, потому что там представлен квадрат соотношения d, деленного на l. Это значение можно было бы охарактеризовать как квадрат некоей тригонометрической функции. Рассмотрим первую строку вавилонской таблички, использовав десятеричную систему. В колонке II обозначена длина катета b=119 (что в шестидесятеричной системе записывается как 159 — одна «шестидесятая» плюс 59. — Примеч. перев.), а в колонке III — гипотенуза d =169 (записано как 249 — две «шестидесятой» плюс 49). Из этих величин вытекает длина другого катета, l = = 120 (200 — две «шестидесятки»). В таблице ниже эти значения переведены в десятеричную систему, по ней легче проверить соответствующие соотношения.
| Номер строки | l | b | d |
| 1 | 120 | 119 | 169 |
| 2 | 3456 | 3367 | 4825 |
| 3 | 4800 | 4601 | 6649 |
| 4 | 13500 | 12709 | 18541 |
| 5 | 72 | 65 | 97 |
| 6 | 360 | 319 | 481 |
| 7 | 2700 | 2291 | 3541 |
| 8 | 960 | 799 | 1249 |
| 9 | 600 | 481 | 769 |
| 10 | 6480 | 4961 | 8161 |
| 11 | 60 | 45 | 75 |
| 12 | 2400 | 1679 | 2929 |
| 13 | 240 | 161 | 289 |
| 14 | 2700 | 1771 | 3229 |
| 15 | 90 | 56 | 106 |
ЗЕМЛЕМЕРИЕ В ЕГИПТЕ
В Египте математика была менее развита, чем в Междуречье. Сведения о ней происходят из пяти папирусов, посвященных математическим вопросам, среди которых самые важные — это папирус Ринда, обнаруженный в 1858 году шотландским египтологом Александром Генри Риндом (1833-1863) и ныне хранящийся в Британском музее, и Московский папирус, находящийся в коллекции Пушкинского музея в Москве. Два этих документа восходят, по всей видимости, к XVIII веку до н.э., хотя, возможно, они еще более древние. Оба папируса представляют исключительную ценность для историков математики, и весьма показательно, что ни в одном из них нет никаких свидетельств о теореме, известной сегодня как теорема Пифагора, или о пифагоровых тройках.
Во всяком случае, египтяне знали о том, что треугольники с соотношением сторон 3, 4, 5, а также пропорциональные им, прямоугольные и широко пользовались этим соотношением, когда надо было начертить две перпендикулярные линии, так что треугольник 3:4:5 даже получил название египетского.
О его применении, среди прочих, рассказывает Геродот в своем описании работы землемеров после сдвигов почвы, вызванных разливами Нила. Засвидетельствовано использование египетского треугольника и в строительстве, к примеру, при возведении огромной пирамиды Хефрена, восходящей к XXVI веку до н.э.
Ясное указание на пифагорово соотношение появляется в различных египетских расчетах, однако до нас не дошло никаких свидетельств, что это соотношение было сформулировано в общей форме. К примеру, в одном из документов XII династии (ок. 2000 до н.э.), найденном в Кахуне, используется выражение
l2 = (3/4)2 = (1+1/4)2,
пропорциональное египетскому треугольнику. В Берлинском папирусе тоже содержится ряд медицинских, литературных и математических документов Среднего Царства, содержащих следы пифагоровой теоремы. В одном из математических папирусов решается система уравнений с двумя неизвестными в связи со следующей задачей:
Площадь квадрата в 100 квадратных кубитов равна сумме двух меньших квадратов. Сторона одного из них составляет 1/2 + 1/4 стороны другого. Найди длины сторон этих квадратов.
ТРИАНГУЛЯЦИЯ В ЗЕМЛЕМЕРИИ
Египетские землемеры были жрецами, и их деятельность по измерению земли имела почти мистическое значение и вызывала благоговение у крестьян. Способ, с помощью которого они творили свое «волшебство», — это не что иное, как тригонометрия. Первые культуры, которые заинтересовались геометрией, развивали тригонометрические знания для использования их в строительстве и землемерии. Раздел земель на треугольники (триангуляция) всегда был главным методом измерения поверхностей, и развитие топографии вплоть до наших дней доказало его эффективность. Каждый треугольник можно разбить на два прямоугольных треугольника, которые позволят определить высоту или расстояние до недостижимых объектов с помощью измерения некоторых сторон и некоторых треугольников. Внимательно рассмотрев эти фигуры и сопоставив их с определениями синуса, косинуса и тангенса (см. стр. 55), можно заметить их очень полезные свойства. К примеру, b = a tg В. То есть вычислив угол В, можно получить значение а и, с помощью тригонометрических таблиц, узнать длину b. Это позволяет реализовать любые технические измерения с помощью линейки и теодолита (инструмент для точного измерения углов на местности), которые точно определяют длины и углы.

Английская гравюра начала XVII века, иллюстрирующая измерение расстояния до недостижимого объекта с помощью триангуляции.
На языке современной алгебры соответствующая задача решается следующей системой:
х2 + у2 = 100,
y = (1/2 + 4/4)x
что требует, как это видно в папирусе, выполнить подстановку и вычислить квадратный корень. Это решение типологически близко пифагорову, но более, чем о знакомстве с теоремой Пифагора, оно свидетельствует о том, что египтянам были известны методы решения двойных уравнений — значительный результат для Древнего Египта.
ПИФАГОР В ИНДИИ
В Индии также развивались арифметико-геометрические знания, связанные с теоремой Пифагора, — они применялись при строительстве храмов и возведении алтарей. Между VIII и II веком до н. э. арифметические и геометрические сведения составили сборник текстов, известный под названием «Сульвасутра». Сульва — это термин, обозначающий веревки, использующиеся для измерения, а Сутра — книга правил и изречений, относящихся к определенному ритуалу или науке, так что название можно перевести как «Учебник правил о веревке».
Тексты «Сульвасутры» были своего рода сборником книг, где излагались правила возведения алтарей определенных форм и размеров, среди которых самые интересные — это «Баудхаяна» и «Апастамба», датируемые V веком до н. э. Там излагаются способы использования веревки не только для измерения, но и для построения перпендикулярных линий — для этого применяются три веревки, длины которых представляют пифагоровы тройки (к примеру, 3, 4, 5; 5, 12, 13; 8, 15, 17; 7, 24, 25). Для этих целей использовали чаще всего треугольник со сторонами 15, 36, 39 (пропорциональный треугольнику 5, 12, 13, называемому индийским треугольником).
Трудно оценить, насколько оригинальны эти сведения для Индии. С одной стороны, здесь, как и в Египте, использовалось натяжение веревок, а с другой — все тройки «Сульвасутры» легко отыскать в вавилонском правиле, описанном выше. Это наводит на мысли о том, что знания из Месопотамии пришли и на берега Инда.
ПОЭЗИЯ И МАТЕМАТИКА В КИТАЕ
В Китае теорема Пифагора известна как Кон Ку и впервые появляется в математическом трактате «Чу Пей Cyan Чинь», что можно перевести как «Классическая арифметика гномона». Наиболее вероятно, что этот труд был написан между 500 и 300 годами до н. э., и, по общему мнению, Пифагор его знать не мог. «Чу Пей Суан Чинь» — это сумма знаний, пришедших из гораздо более отдаленных времен и собранных в III веке до н.э. двумя знаменитыми математиками, Чжао Шуаном и Лю Хуэем. К счастью, в его содержании можно отделить древние пласты от позднейших наслоений. Что касается теоремы Пифагора, этот математический трактат касается ее только в примитивной форме, то есть дает конкретные числовые соотношения, а не общие правила нахождения пифагоровых троек.
В трактате «Чу Пей Суан Чинь» есть один пассаж о прямоугольных треугольниках, в котором интерес вызывает описание некоей фигуры, названной диаграммой гипотенузы и представляющей собой не что иное, как визуальную демонстрацию теоремы Пифагора с помощью треугольника со сторонами а = 3, b = 4 и с = 5. В этом доказательстве строится квадрат со стороной (а + b)у который делится на четыре треугольника с основанием а и высотой b, и квадрат со стороной с (см. рисунок 3 на следующей странице). В высшей степени вероятно, что доказательство восходит к эпохе уже после Пифагора, но даже в этом случае его стоит разобрать подробнее.
Дан прямоугольный треугольник с катетами а и b и гипотенузой с. Следует доказать, что площадь квадрата со стороной с равна сумме площадей квадратов со сторонами а и b.
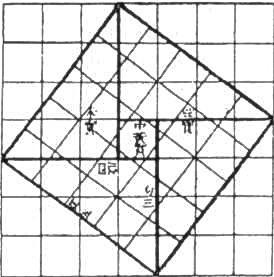
РИС. з
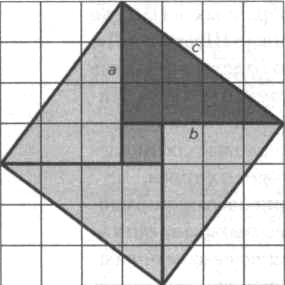
РИС. 4
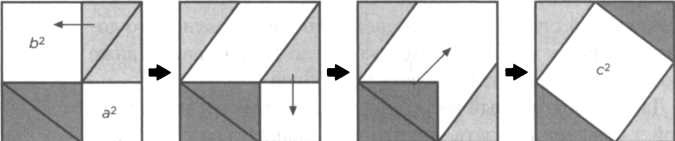
РИС. 5
Если к исходному треугольнику присоединить три равных ему треугольника внутри квадрата со стороной с (см. рисунок 4), то в центре этого квадрата останется незанятым меньший квадрат. Можно заметить, что сторона этого меньшего квадрата равна b - а. Таким образом, площадь меньшего квадрата можно выразить как (b - а)2 = b2 - 2ab + a2, учитывая, что (b - а)2 = (а - b)2. Площадь квадрата со стороной с представляет собой площадь четырех квадратов с высотой а и основанием b, плюс площадь маленького квадрата, таким образом, теорему можно считать доказанной:
с2 = 4(ab/2) + a2 - 2ab + b2 = а2 + b2.
«Чу Пей Суан Чинь» содержит и еще одно блестящее доказательство с применением простого переноса частей (см. рисунок 5).
Второй классический китайский трактат, в котором рассматриваются геометрические аспекты, связанные с теоремой Пифагора, датируется примерно 250 годом до н.э., хотя Лю Хуэй откомментировал его и переписал в 263 году.
Речь идет о «Дзю Чжан Суань Шу»> что значит «Математика в девяти книгах». Последняя, девятая глава полностью посвящена прямоугольным треугольникам и представляет собой 24 задачи, решения которых в той или иной степени основаны на теореме Пифагора. Самая известная из них — задача о сломанном бамбуке, в которой описывается прямоугольный треугольник, образованный сломанным стволом бамбука:
Бамбук высотой 10 футов сломан так, что его верхушка опирается на землю на расстоянии в три фута от основания. Надо вычислить, на какой высоте находится место излома.
Решение этой задачи сочетает в себе теорему Пифагора и применение квадратных уравнений, так как представляет собой решение уравнения
х2 + З2 = (10 - х)2.
ПИФАГОР: ТРАДИЦИОННЫЕ ДОКАЗАТЕЛЬСТВА
Пифагор не оставил потомкам ни строчки, так что не существует ни одного доказательства теоремы, авторство которого можно было бы приписать ему. Ее решение дается во множестве источников, вплоть до детального описания его в самой важной в истории геометрии книге «Начала» Евклида. Но в любом случае не стоит отказывать Пифагору и его последователям в определенной гениальности, так как именно они совершили переход от частного к общему и сформулировали теорему, применимую ко всем частным случаям.
Первое доказательство теоремы, которую традиция приписывает Пифагору, было эмпирическим. Берется треугольник со сторонами a, b, c (катеты и гипотенуза), на которых строятся три квадрата согласно строгим правилам греческой геометрии (см. рисунок 6). Из этих квадратов складываются два различных квадрата. Первый получается из двух квадратов, построенных на катетах и четырех прямоугольных треугольников, каждый из которых равен исходному треугольнику (см. рисунок 7). Второй квадрат состоит из тех же четырех треугольников и квадрата, построенного на гипотенузе (см. рисунок 8). Если из обоих квадратов убрать эти треугольники, площадь центрального квадрата второго (с2) будет равна площади двух малых квадратов первого (b2 + а2), что доказывает теорему Пифагора.
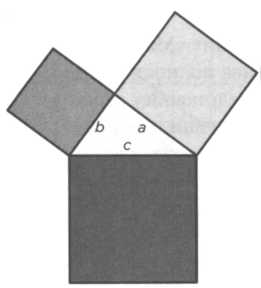
РИС. 6

РИС. 7

РИС. 8
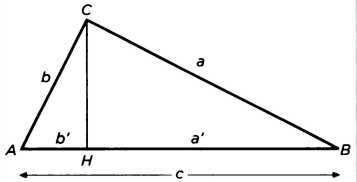
РИС. 9
В противовес такому графическому доказательству, основанному на теории пропорций Пифагора, — теории несовершенной, так как она применима только к соизмеримым количествам, — некоторые историки математики выдвигают другое доказательство, алгебраического характера. Пифагор мог доказать теорему через подобие треугольников — на рисунке 9 треугольники АВС, АСН и СВН — с пропорциональными соответствующими сторонами. Возьмем треугольник АВС с прямым углом С, для которого отрезок СН представляет собой высоту, опущенную на гипотенузу, и делит ее на отрезки d и V — проекции, соответственно катетов а и b. Прямоугольные треугольники АВС, АСН и СВН имеют три общие стороны: каждый из треугольников имеет по две стороны, общие с другими, а их острые углы равны, так как они либо общие, либо составляют вместе прямой угол. Таким образом, треугольники подобны.
ДОКАЗАТЕЛЬСТВО ЧЕРЕЗ ПОДОБИЕ ТРЕУГОЛЬНИКОВ
Подобие треугольников можно применить двумя способами.
— Подобие треугольников АВС и АСН: два треугольника подобны, когда два или более угла у них конгруэнтны (что доказал Евклид):
b/b' = c/b
b2 = b'c.
— Подобие треугольников АВС и СВН:
a/a' = c/a
a2 = a'c.
из чего вытекает так называемая теорема катета. Суммируем:
а2 + b2 = а'с + b'с = с(а' + b'),
но (а' + b') = с, из чего следует
а2 + b2 = с2.
«НАЧАЛА» ЕВКЛИДА
Евклид жил в Александрии около 300 года до н.э. и был автором «Начал» (Stoicheia) — труда, оказавшего огромное влияние на развитие математики и науки в целом. В этой книге он собрал все геометрические знания своей эпохи, не считая собственных доказательств, изложенных строго и изящно, включая определения, формулировки и общие сведения. Этот труд был не просто блестящим компендиумом, а серьезной работой по упорядочиванию геометрических знаний. Возможно, именно поэтому вплоть до последнего времени эта книга оставалась эталоном геометрического трактата. «Начала» занимают второе место по количеству изданий и переводов, уступая только Библии. К настоящему времени они выдержали более тысячи переизданий.
«Начала» делятся на 13 книг: четыре первые посвящены основам планиметрии — конгруэнтность треугольников, равенство площадей, золотое сечение, круг, правильные многоугольники, некоторые квадратуры и, естественно, теорема Пифагора (книга I, предложение 47). Свойства теоремы Пифагора используются в геометрическом контексте измерения площади фигур. Теорема Пифагора вновь упоминается в книге VI, а также в книге X, где речь идет о квадратных корнях.
В предложении 47 Евклид постулирует, что в квадратных треугольниках квадрат стороны, противоположной прямому углу, равен сумме квадратов сторон, прилегающих к нему. Иллюстрация к этому утверждению получила название «ветряной мельницы» (см. рисунок).
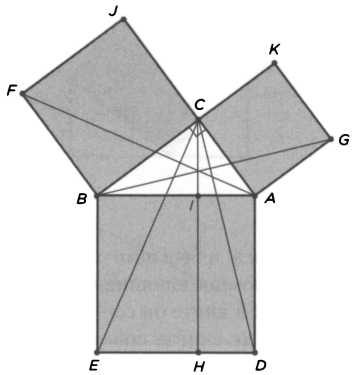
Доказательство выполняется с помощью расчета площадей. Оно заключается в том, чтобы доказать равенство треугольников BFA и ВСЕ и то, что их удвоенная площадь равна, с одной стороны, площади квадрата CBFJ, а с другой — площади прямоугольника ВШЕ. Таким же образом квадрат CKGA имеет ту же площадь, что и прямоугольник AIHD. Отсюда выводится теорема Пифагора, которую можно сформулировать следующим образом: площадь квадрата BADE равна сумме площадей квадратов CBFJ и CKGA.
ЕВКЛИД ИЗ АЛЕКСАНДРИИ
Евклида считают отцом геометрии.
Хотя, по всей вероятности, ни один из результатов в «Началах» не является его открытием, нет сомнений, что именно Евклиду мы обязаны структурированием сведений и способом их изложения. О его жизни известно мало — почти исключительно те сведения, которые сообщает философ Прокл (V век) в своих комментариях к книге I «Начал».
По словам Прокла, Евклид родился ок. 325 года до н.э., жил и преподавал в Александрии и умер прибл. в 265 году до н.э. Кроме того, Прокл утверждает (и это выглядит весьма правдоподобным), что, судя по особенностям его работы, Евклид, возможно, обучался в школе Платона или у кого-то из его учеников. Таким образом, по сведениям Прокла, Евклид жил в эллинистический период. Это более вероятно, чем то, что он жил в классической Греции, учитывая, что в его книге есть отсылки к знаниям той эпохи. Так, Евклид сгруппировал описываемые им открытия способом, непохожим на то, как это делали греки классического времени. Тот же Прокл говорит, что Евклид собрал результаты философа и математика Евдокса (ок. 390-337 до н.э.) в области теории пропорций и математика Теэтета (ок. 417-369 до н.э.) в области правильных многоугольников и что в целом представил в своей книге неопровержимые доказательства множества теорем своих предшественников, о которых дошли лишь скудные сведения. Не сохранилось изначальной редакции труда самого Евклида, так что его тексты приходится реконструировать по комментариям и заметкам более поздних авторов, особенно византийских, латинских и арабских.

Евклид, занимающийся геометрией. С рельефа Андреа Пизано, XIV век (Музей Домского собора, Флоренция).
Теорема показывает также, как получить квадрат, по площади равный двум заданным квадратам, то есть как найти такое значение х, при котором х2 = а2 + b2, так что это еще один пример применения геометрической алгебры. Если предложение 47 представляет собой кульминацию первой книги «Начал», то еще более интересно, как впоследствии Евклид доказывает теорему, ей обратную. Это предложение 48, которому обычно уделяется не так много внимания, но которое имеет огромное логико-дедуктивное значение. В нем постулируется, что если в треугольнике квадрат одной из сторон равен сумме квадратов двух других, то угол, который образуют эти стороны, прямой (см. рисунок 10).
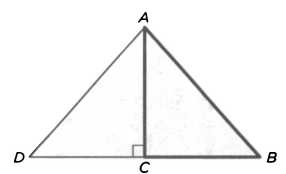
РИС. 10
Доказательство состоит в том, чтобы построить отрезок CD, перпендикулярный АС и равный СВ. Согласно заданным условиям:
ВС2+АС2=АВ2,
и, так как треугольник ADC прямоугольный,
АС2 + CD2=AD2.
Поскольку ВС = CD, АВ2 = AD2, то, следовательно, АВ = AD. Следовательно, треугольники ADC и АВС конгруэнтны, а угол АСВ, равный углу ACD, прямой.
Евклид приводит и графическое доказательство, где квадраты, выстроенные на катетах, превращаются в параллелограммы той же площади (так как они имеют то же основание и ту же высоту), а те, в свою очередь, трансформируются в квадрат, построенный на гипотенузе. Это гениальное доказательство представлено на рисунке 11.
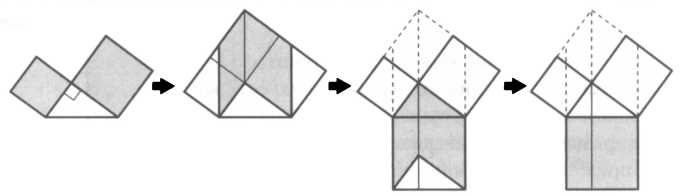
РИС. 11

Оксирннхский папирус 29, фрагмент «Начал», датированный II—IV веками (Филадельфия).

Фрагмент «Афинской школы» Рафаэля, Евклид изображен с циркулем. С противоположной стороны фрески находится Пифагор (Рим).
Теорема Пифагора числится среди имеющих наибольшее число возможных способов доказательства. Одно из объяснений этого явления в том, что в Средние века представление нового способа ее доказательства было одним из условий получения степени Magister matheseos, то есть магистра математики, и в известном смысле это умение стало со временем универсальным показателем общего образования человека.
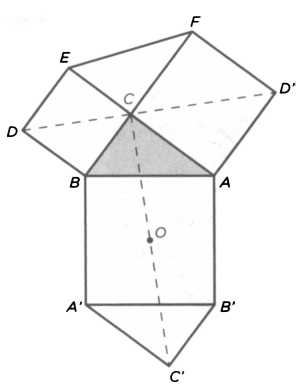
РИС. 12
Гениальный Леонардо да Винчи (1452-1519) был образцом универсального человека эпохи итальянского Возрождения, поскольку блестящим образом сочетал в себе знания в самых разных областях — как в сфере науки, так и искусства. Человек, который запечатлел таинственную красоту Джоконды и изобрел бесчисленные удивительные механизмы, смог представить собственное блестящее доказательство теоремы Пифагора. Леонардо основывался на знаменитой фигуре «мельницы», то есть треугольника с квадратами, построенными на трех его сторонах. К ним сверху он добавил треугольник ECF, а снизу разместил копию исходного треугольника А'С В' (см. рисунок 12). Проведя отрезки DD' и СС', служащие друг другу перпендикулярами, можно убедиться, что DD' делит верхний шестиугольник ABDEFD' на симметричные половины, которыми, если их развернуть друг относительно друга, можно полностью накрыть шестиугольник АСВА'С'В'. Следовательно, два квадрата, построенные на катетах, в сумме дают площадь, равную площади квадрата, построенного на гипотенузе.
ТЕОРЕМА ПИФАГОРА СЕГОДНЯ
Спустя два с половиной тысячелетия после открытия теорема Пифагора находит самые разные математические и научные способы применения. Это математическое достижение, оказавшееся, возможно, столь живучим благодаря своей простоте, сохраняет свою важность при вычислении длин, площадей и объемов разнообразных фигур. В квадрате со стороной х диагональ будет равна х√2; в прямоугольнике со сторонами х и у диагональ равна √(х2 + у2); в параллелограмме (например, в коробке из- под обуви) размерами х, у, z диагональ составит √(х2 + у2 + z2); в конусе с высотой h и радиусом основания r образующая равняется √(h2 + r2)... и так можно продолжать очень долго.
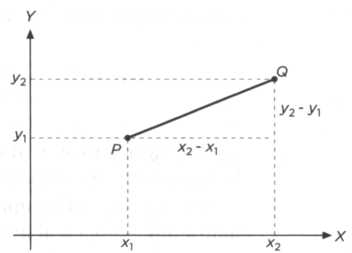
РИС. 13
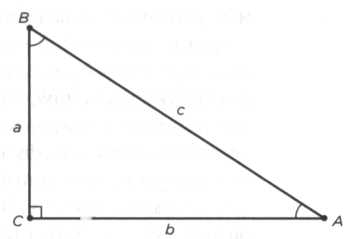
РИС. 14
Теорема Пифагора также лежит в основе декартовой системы координат на плоскости и в пространстве и позволяет определить расстояние d(P,Q) между двумя точками Р= (x1,y1) и Q= (х2, у2), как показано на рисунке 13. Применяя теорему, получаем:
Расстояние (P,Q) = √((x2 - x1)2 + (y2 - y1)2)·
В любом расчете, который предусматривает применение функций, проявляется пифагорово отношение, учитывая, что y = ƒ(x) в декартовом выражении. Теорема используется и в тригонометрии. С величинами углов прямоугольного треугольника связаны такие функции, как синус, косинус, тангенс... (см. рисунок 14), так что:
sin А = a/c cos А = b/c tg А = a/b.
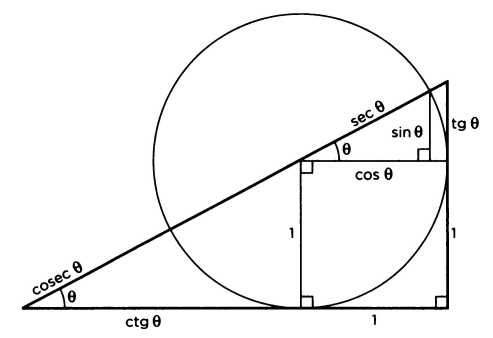
Таким образом, в тригонометрических терминах теорему Пифагора можно выразить как отношение sin2 А + cos2 А = 1. Теореме можно найти применение в топографии, картографии, навигации — морской или воздушной, — а также, конечно, в архитектуре, инженерном деле и во всех областях человеческой деятельности, где требуется расчет размеров. Чтобы показать исключительную важность теоремы в тригонометрии, можно привести следующий рисунок. Кроме того, что на нем мы видим круг и прямоугольный треугольник, катеты которого представляют собой синус и косинус, этот рисунок демонстрирует нам и многие другие величины, соответствующие большинству тригонометрических функций. Там можно найти тангенс, представляющий собой соотношение между синусом и косинусом, три взаимозависимых функции: секанс (то есть 1, деленное на косинус), косеканс (функция, обратная синусу) и котангенс (функция, обратная тангенсу). Таким образом, благодаря вездесущей теореме Пифагора приведенный на рисунке прямоугольный треугольник позволяет вывести очень много интересных соотношений, среди которых шесть тригонометрических функций.
tg2θ +1 = sec2θ,
ctg2θ +1 = cosec2θ,
(tg θ +1 )2 + (ctg θ +1 )2 = (sec θ + cosec θ)2.
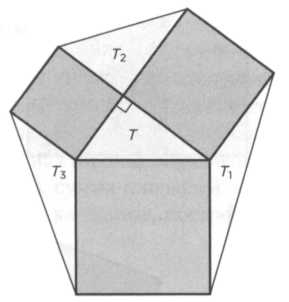
РИС. 15
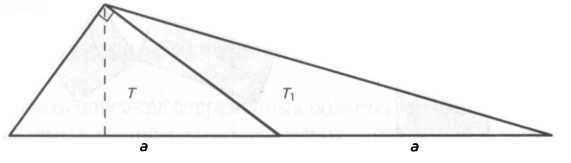
РИС. 16
ТЕОРЕМА ПИФАГОРА В ДРУГИХ МНОГОУГОЛЬНИКАХ
Нет сомнений, что пифагорово соотношение тесно связано с конкретной геометрической фигурой — прямоугольным треугольником. Однако если принять во внимание классическое изображение этой теоремы в виде «ветряной мельницы», где три квадрата составлены так, что их стороны образуют катеты и гипотенузу прямоугольного треугольника, сами собой появляются некоторые вопросы. Что будет, если использовать квадраты для построения любого треугольника? Что будет, если они образуют параллелограмм?
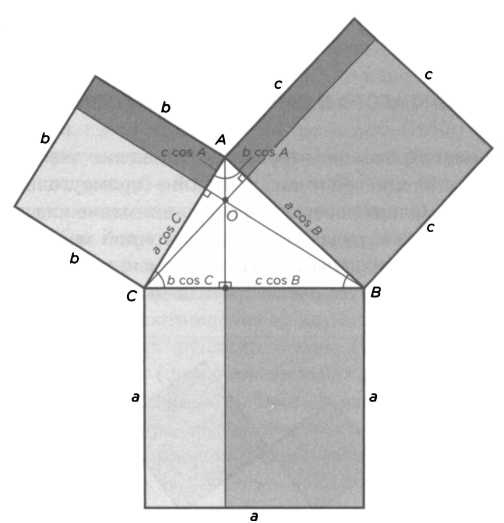
РИС. 17
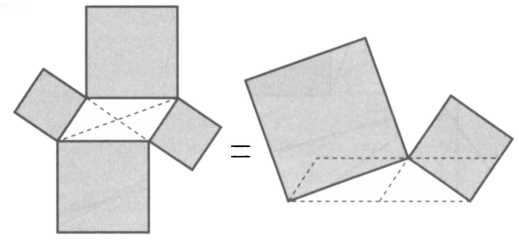
РИС. 18
Если соединить тремя отрезками квадраты при прямоугольном треугольнике, образуется шестиугольник, в котором
появятся три новых треугольника с площадями Т1, Т2 и Т3 (см. рисунок 15). Каковы их площади? Во всех случаях их площади в точности равны площади исходного треугольника: Т1 = Т2 = Т3 = Т. На рисунке 16 показано, что Т = Т1, так как у обоих треугольников одинаковы основание и высота. Для других треугольников также действительно это соотношение. Если взять любой произвольный треугольник АВС, то можно построить на его сторонах три квадрата и задать вопрос, каково соотношение площадей этих квадратов. Возьмем, к примеру, треугольник с острым углом (A < 90°). Решение показано на рисунке 17. На нем проведены три высоты треугольника. Эти высоты продолжены так, чтобы соответствующие прямые делили каждый квадрат, построенный на сторонах треугольника, на два прямоугольника. Подставляя длины сторон, получаем, что площадь верхнего правого прямоугольника равна с · (a cos В). Удивительно, что такова же и площадь нижнего правого прямоугольника. Площади секций слева равны b · (a cos С). Добавляем еще два сегмента с площадями b · (с cos А) и получаем результат:
a2 = b2 + c2 - 2 · b · c · cosA,
по закону косинуса.
Таким образом, если А = 90°, cos 90°= 0, и мы получаем b2 + с2 = а2, известное пифагорово соотношение. Таким образом, закон косинуса — это продолжение теоремы Пифагора. Еще одно удивительное свойство проявляется, если построить четыре квадрата на сторонах параллелограмма. Как можно видеть на рисунке 18, сумма площадей этих квадратов равна сумме площадей двух квадратов, построенных на диагоналях параллелограмма.
МАТЕМАТИЧЕСКИЕ РАЗВЛЕЧЕНИЯ
Закончить описание современных областей применения одного из самых великих математических достижений в истории можно парой развлекательных задачек. Во-первых, теорема Пифагора позволяет ответить на вопрос, которым люди задавались с того момента, как узнали о кривизне земной поверхности: на каком расстоянии от нас находится видимый горизонт? Чтобы ответить, надо знать лишь высоту над уровнем моря, на которой находится наблюдатель. К примеру, если он стоит, озирая окрестности, на горе высотой 1000 м, можно применить нашу теорему следующим образом:
(R + h)2 = R2 + v2.
Следовательно:
v2 = (R+h)2 - R2 = (R2 + 2Rh + h2) - R2 = h2 + 2Rh = h(h+2R),
где R — радиус Земли. Так как 2R + h ≈ 2R, поскольку h значительно меньше R, получается:
v2 ≈ h(2R)
v ≈ √(2Rh).
И так как R = 6371 км, a h = 1 км, получаем:
v ≈ 112, 88 км.
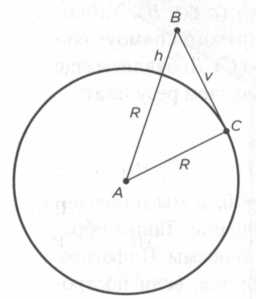
РИС. 19
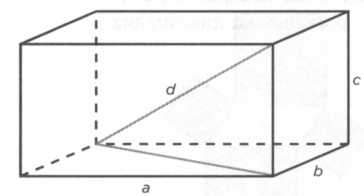
РИС. 20
И наконец, зная соотношение Пифагора как типичное свойство плоских прямоугольных треугольников, можем ли мы применить теорему к трехмерным фигурам? Да, сделать это можно разными способами. Известный и наиболее наглядный — выразить диагональ d коробки со сторонами a, b, с через теорему Пифагора: d2 = а2 + b2 + с2 (см. рисунок 20).
Назад: ГЛАВА 1 Правда и миф о Пифагоре
Дальше: ГЛАВА З Пифагорейское братство

