Глава 2. Коды и комбинации

Азбуку Морзе придумал Сэмюэл Финли Бриз Морзе (1791–1872). Это изобретение неотделимо от создания телеграфа, о работе которого нам также предстоит узнать. Азбука Морзе послужила хорошим вводным материалом для знакомства с сущностью кода, а телеграф – такой же удобный пример, иллюстрирующий аппаратное обеспечение компьютера.

Многим кажется, что азбуку Морзе проще передавать, чем принимать. Даже если вы не знаете ее на память, можете просто сверяться с , где буквы для удобства расставлены по алфавиту.

Принимать азбуку Морзе и переводить ее в обычные слова значительно сложнее и дольше, поскольку вы работаете в обратном порядке: выясняете, какая буква соответствует конкретной кодовой последовательности точек и тире. Например, если вы получите сигнал «тире-точка-тире-тире», придется заглянуть в таблицу и просмотреть почти все буквы одну за другой, пока не выяснится, что перед вами Ы.

Проблема в том, что у нас есть таблица для следующего перевода:

Однако нет обратной таблицы:

В начале изучения азбуки Морзе такая таблица, безусловно, пригодилась бы. Правда, не вполне понятно, как ее составить. Точки и тире не допускают никакого подобия алфавитного порядка.

Давайте забудем об алфавите. Пожалуй, разумнее сгруппировать коды таким образом, чтобы их расстановка зависела от количества точек и тире в той или иной букве. Так, последовательность из азбуки Морзе, содержащая одну точку и одно тире, может означать всего одну из двух букв: Е или Т.

Комбинации, в которых содержится по два знака (либо точки, либо тире), дают нам уже четыре буквы: И, А, Н и М.

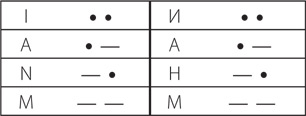
Паттерн из трех символов, точек или тире, дает нам восемь букв: С, Д, У, К, Р, Г, О, В.

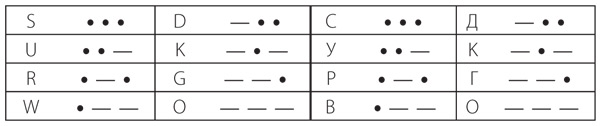
Наконец (если мы хотим прекратить это упражнение, пока не перешли к цифрам и знакам препинания), четырехзначные последовательности точек и тире дают нам еще 16 символов.

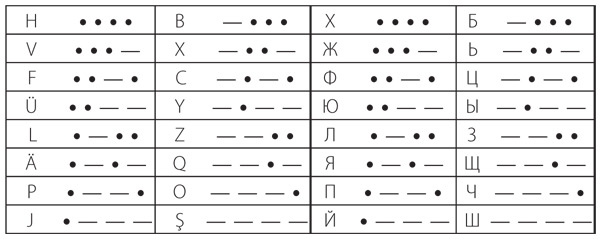
Всего в этих таблицах содержится 2 + 4 + 8 + 16 кодов суммарно для 30 букв; это на четыре кода больше, чем требуется для полной латиницы, состоящей из 26 букв. Именно поэтому четыре кода в последней таблице отведены под буквы с диакритическими знаками.

Эти четыре таблицы помогут с легкостью переводить любые сообщения, передаваемые азбукой Морзе. Получив код конкретной буквы, вы считаете, сколько в нем точек и тире, и решаете, с какой из таблиц сверяться. Каждая таблица устроена так, что код, состоящий из одних точек, располагается в верхнем левом углу, а код из одних тире – в нижнем правом углу.

Замечаете закономерность в размерах четырех таблиц? Обратите внимание: в каждой следующей таблице вдвое больше кодов, чем в предыдущей. Это логично: в последующей таблице содержатся все коды из предыдущей «плюс точка», а также все коды из предыдущей «плюс тире».

Эту тенденцию можно резюмировать следующим образом.

Каждая из четырех таблиц содержит вдвое больше кодов, чем предшествующая ей таблица, так что если в первой таблице 2 кода, то во второй – 2 × 2 кодов, в третьей – 2 × 2 × 2 кодов. Вот как еще можно это представить.

Разумеется, при умножении числа самого на себя можно использовать степени. Так, 2 × 2 × 2 × 2 можно записать как 2⁴ (2 в четвертой степени). Числа 2, 4, 8 и 16 являются степенями двойки, поскольку представляют произведения, которые можно получить умножением двойки самой на себя. Итак, нашу таблицу можно переписать и так.

Таблица сильно упростилась. Количество кодов равно просто 2 в степени <количество точек и тире>. Можно резюмировать табличные данные в виде простой формулы:

Степени двойки часто используются в различных кодах (другой пример рассмотрим в следующей главе).

Чтобы еще сильнее упростить расшифровку кода Морзе, давайте попробуем построить большую древовидную схему на следующей странице.

На схеме показано, какие буквы получаются при постепенном усложнении последовательностей точек и тире. Чтобы расшифровать конкретную последовательность, идите по стрелкам слева направо. Допустим, мы хотим выяснить, какая буква соответствует коду «точка-тире-точка». Начинаем слева, берем точку; далее идем по стрелкам, выбираем тире, а затем еще одну точку. Получаем букву R, расположенную около последней точки.

Такая схема необходима прежде всего для того, чтобы определить код Морзе. Во-первых, она страхует от тупой ошибки: не дает присвоить двум разным буквам один и тот же код. Во-вторых, вы гарантированно задействуете все возможные коды, не выстраивая чрезмерно длинных последовательностей из точек и тире.

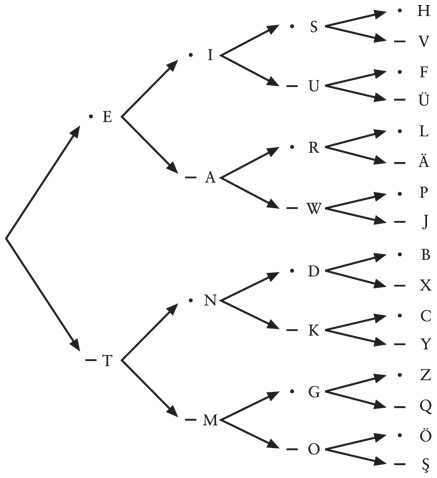
Рискуя получить схему, которая не поместится на печатной странице, мы могли бы расширить ее и добавить туда пятизначные коды из точек и тире. Последовательность из пяти точек и тире даст нам 32 (2 × 2 × 2 × 2 × 2, или 2⁵) дополнительных кода. Как правило, этого достаточно не только для букв, но и для 10 цифр и 18 знаков препинания, включаемых в азбуку Морзе: цифры действительно кодируются пятизначными последовательностями точек и тире. Правда, многие другие пятизначные коды зарезервированы не за знаками препинания, а за буквами с диакритическими знаками.

Чтобы система учитывала все знаки препинания, в нее нужно включить последовательности из шести точек и тире. Таким образом получим 64 (2 × 2 × 2 × 2 × 2 × 2, или 2⁶) дополнительных кода для суммарного множества из 2 + 4 + 8 + 16 + 32 + 64, или 126, символов. Для азбуки Морзе этого слишком много, поэтому большинство таких длинных кодов остаются неопределенными. Слово «неопределенный» в данном контексте указывает на код, который ничего не означает. Если бы вы, принимая азбуку Морзе, получили неопределенный код, то могли бы почти не сомневаться, что кто-то просто допустил ошибку.

У нас хватило смекалки построить эту небольшую формулу:

Так давайте продолжим нашу таблицу и посмотрим, сколько кодов получится из более длинных последовательностей точек и тире.

К счастью, нет необходимости выписывать все возможные коды, чтобы определить, сколько их будет. Достаточно умножать двойку на себя нужное количество раз.

Код Морзе называется двоичным (что буквально означает «два на два»), поскольку любой его элемент включает только два компонента: точку и тире. Такой код подобен монете, которая может упасть только решкой или орлом. Двоичные объекты (например, монеты) и двоичные коды (например, азбука Морзе) всегда можно описать в виде степеней двойки.

Проделанный нами анализ двоичных кодов – это простое упражнение в одной математической дисциплине, которая называется комбинаторикой, или комбинаторным анализом. Традиционно комбинаторный анализ особенно активно используется в теории вероятностей и статистике, поскольку связан с выявлением количества вариантов комбинаций различных объектов (например, монет или игральных костей). Он также помогает понять, как составляются и разбираются коды.