Книга: Код. Тайный язык информатики
Назад: Глава 22 Операционная система
Дальше: Глава 24 Языки высокого и низкого уровня
Глава 23
Фиксированная точка, плавающая точка
В повседневной жизни мы легко оперируем целыми числами, дробями и процентами одновременно. Мы покупаем полдесятка яиц, заплатив налог в размере 8¼ процента из денег, полученных за 2¾ часа сверхурочной работы, оплаченной по тарифу, в полтора раза превышающему обычный. Большинство людей не испытывают трудностей при использовании таких величин. Услышав от статистиков о том, что «среднее американское домохозяйство состоит из 2,6 человека», мы не ужасаемся при мысли о связанных с этим повсеместных увечьях.
Тем не менее когда дело касается компьютерной памяти, переключение между целыми и дробными числами оказывается сложнее. Да, все данные хранятся в компьютерах в виде битов, то есть в виде двоичных чисел. Однако одни виды чисел выразить в битах гораздо легче, чем другие.
Сначала мы использовали биты для представления положительных целых или положительных натуральных чисел. Мы также узнали, как с помощью дополнения до двух можно отобразить отрицательные целые числа, чтобы упростить операцию сложения. В следующей таблице показано, какие диапазоны положительных и отрицательных целых чисел (отрицательные числа выражены с помощью дополнения до двух) можно хранить в ячейках памяти емкостью 8, 16 и 32 бит.
Число битов
Диапазон целых положительных чисел
Диапазон целых отрицательных чисел
8
От 0 до 255
От –128 до 127
16
От 0 до 65 535
От –32 768 до 32 767
32
От 0 до 4 294 967 295
От –2 147 483 648 до 2 147 483 647
Однако на этом мы и остановились. Помимо целых чисел математики также различают рациональные числа, которые могут быть представлены в качестве отношения двух целых чисел. Это отношение также называется дробью. Например, дробь ¾ — рациональное число, отношение чисел 3 и 4. Это число также можно записать в виде десятичной дроби: 0,75. Десятичная дробь остается отношением двух чисел, в данном случае 75/100.
В главе 7 рассказывалось, что в десятичной системе счисления цифры слева от десятичного разделителя являются множителями целых положительных степеней числа 10, а цифры справа — множителями целых отрицательных степеней числа 10. В одном из примеров я показал, что число 42 705,684 равно:
4 × 10 000 +
2 × 1000 +
7 × 100 +
0 × 10 +
5 × 1 +
6 ÷ 10 +
8 ÷ 100 +
4 ÷ 1000.
Обратите внимание на знаки деления. Затем я представил эту последовательность операций без деления:
4 × 10 000 +
2 × 1000 +
7 × 100 +
0 × 10 +
5 × 1 +
6 × 0,1 +
8 × 0,01 +
4 × 0,001.
И наконец, отобразил это число, используя степени числа 10:
4 × 104 +
2 × 103 +
7 × 102 +
0 × 101 +
5 × 100 +
6 × 10–1 +
8 × 10–2 +
4 × 10–3.
Существуют рациональные числа, которые не так легко представить в виде десятичной дроби, например ⅓. Если вы разделите 1 на 3, то получите следующее.
0,33333333333333333333333333333333333333333333333333333…
И так до бесконечности. Подобная дробь называется периодической и записывается 0,(3). Несмотря на то что запись числа ⅓ в виде десятичной дроби выглядит неуклюже, это число по-прежнему является рациональным, поскольку это отношение двух целых чисел. Вот еще один пример: отношение 1/7 можно записать в виде десятичной дроби.
0,1428571428571428571428571428571428571428571428571428571…
Или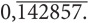
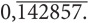
Иррациональные числа — это числа, которые нельзя выразить в виде отношения двух целых чисел, значит, десятичная дробь продолжается бесконечно без повторяющихся последовательностей цифр. К числам такого типа относится квадратный корень из 2.
√2 ≈ 1,41421356237309504880168872420969807856967187537695…
Квадратный корень из 2 — решение следующего алгебраического уравнения:
x2 – 2 = 0.
Если число не является решением какого-либо алгебраического уравнения с целочисленными коэффициентами, оно называется трансцендентным. (Все трансцендентные числа иррациональны, однако не все иррациональные числа трансцендентны.) К трансцендентным числам относится число π, представляющее отношение длины окружности к ее диаметру и приблизительно равное следующему.
3,1415926535897932846264338327950288419716939937511…
Еще одним трансцендентным числом является e, к которому стремится выражение:
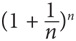
при n, стремящемся к бесконечности. Данное число приблизительно равно следующему.
2,71828182845904523536028747135266249775724709369996…
Все числа, о которых мы говорили, то есть рациональные и иррациональные, называются действительными, или вещественными. Это обозначение отличает их от мнимых — квадратных корней из отрицательных чисел. Комплексные числа — это комбинации мнимых и вещественных чисел. Несмотря на свое название, мнимые числа существуют и используются, например при решении некоторых сложных задач по электронике.
Мы привыкли считать, что числовой ряд непрерывен. Если вы дадите два рациональных числа, я определю, какое число находится между ними. Для этого достаточно найти их среднее арифметическое. Однако цифровые компьютеры не могут работать с континуумами. Биты могут быть равны либо 0, либо 1, между которыми нет больше никаких значений. Так что цифровые компьютеры могут иметь дело только с дискретными значениями. Количество дискретных значений, которые вы можете представить, напрямую связано с количеством доступных битов. Например, в ячейках емкостью 32 бита можно хранить положительные целые числа в диапазоне от 0 до 4 294 967 295. При необходимости сохранить значение 4,5 придется пересмотреть этот подход и действовать иначе.
Можно ли представить дробные значения в двоичном формате? Да, можно. Вероятно, самый простой подход — использование двоично-десятичного кода (BCD). Как говорилось в главе 19, кодировка BCD позволяет записать десятичные числа в двоичном формате. Для кодирования каждой десятичной цифры (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9) требуется четыре бита.
Десятичная цифра
Двоичное значение
0
0000
1
0001
2
0010
3
0011
4
0100
5
0101
6
0110
7
0111
8
1000
9
1001
Формат BCD особенно полезен в компьютерных программах, которые работают с денежными суммами. Самые очевидные примеры — программы для банков и страховых компаний; многие дробные числа в них предусматривают не более двух знаков после десятичного разделителя.
Как правило, для хранения двух BCD-цифр достаточно одного байта. Такая система записи иногда называется упакованным кодом ВСD. В такой кодировке не используется дополнение до двух. По этой причине в случае упакованного кода BCD для указания того, является ли число положительным или отрицательным, обычно требуется дополнительный бит, называемый знаковым битом. Поскольку для хранения BCD-значения удобно выделять целое число байтов, под бит знака обычно отводится четыре или восемь бит памяти.
Предположим, что сумма денег, которой должна оперировать ваша компьютерная программа, никогда не превысит ±10 миллионов долларов. Другими словами, вам требуются значения от –9 999 999,99 до 9 999 999,99. Можно выделить по пять байт памяти для каждой сохраняемой суммы в долларах. Например, число –4 325 120,25 можно представить посредством пяти байт.
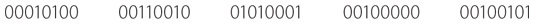
В шестнадцатеричном формате это эквивалентно следующей записи.

Обратите внимание: крайняя левая тетрада равна 1, то есть число является отрицательным. Это знаковый бит. Если бы число было положительным, то крайняя левая тетрада была бы равна 0. Для представления каждой цифры в числе требуется по четыре бита, а прочитать их можно непосредственно по шестнадцатеричным значениям, поскольку они совпадают с десятичными.
Для представления значений в диапазоне от –9 999 999,99 до 9 999 999,99 вам понадобится шесть байт: пять байт для десяти цифр и еще целый байт для знакового бита.
Такой формат записи дробных чисел называется записью с фиксированной точкой, поскольку после десятичного разделителя всегда следует определенное количество цифр, в нашем примере две. Важно: данные о положении этого разделителя не хранятся вместе с числом. Программам, работающим с числами в таком формате, необходимо сообщить, где находится этот разделитель. Вы можете создавать числа с любым количеством десятичных знаков, а также использовать их в одной и той же компьютерной программе. Однако любая часть программы, выполняющая над числами арифметические операции, должна знать, где находится десятичный разделитель.
Формат с фиксированной точкой хорошо работает только в том случае, если вы уверены, что числа не превысят размеры выделенных под них ячеек памяти, что вам не потребуется увеличивать количество десятичных знаков. Использование этого формата совершенно неуместно в ситуациях, когда числа могут стать слишком большими или маленькими. Предположим, вам нужно зарезервировать область памяти для хранения расстояний. Проблема в том, что эти расстояния могут значительно варьироваться. Расстояние от Земли до Солнца составляет 150 000 000 000 метров, а радиус атома водорода — 0,00000000005 метра. Для хранения значений в формате с фиксированной точкой, принадлежащих этому диапазону, придется выделить 12 байт памяти.
Возможно, мы сможем придумать более удобный способ хранения таких чисел, если вспомним, что ученые и инженеры выражают числа с помощью системы, называемой научной нотацией (экспоненциальная запись).
Научная нотация особенно полезна для представления очень больших и очень маленьких чисел, поскольку предусматривает использование степени числа 10, следовательно, позволяет обойтись без длинных строк нулей. В научной нотации следующие числа записываются следующим образом.
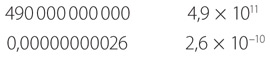
В этих двух примерах числа 4,9 и 2,6 называются дробной частью, или мантиссой (хотя этот термин более уместен для логарифмов). Однако я буду придерживаться компьютерной терминологии, называя этот фрагмент научной нотации значащей частью числа.
Порядок — это степень, в которую возводится число 10. В первом примере порядок равен 11, во втором — –10. Порядок показывает, на сколько мест был сдвинут десятичный разделитель в значащей части числа.
Существует соглашение, по которому значащая часть числа должна принадлежать интервалу от 1 (включительно) до 10. Несмотря на то что следующие числа равны, первый вариант представления является предпочтительным:
4,9 х 1011 = 49 х 1010 = 490 х 109 = 0,49 х 1012 = 0,049 х 1013.
Такая форма научной нотации иногда называется нормализованной.
Обратите внимание: знак показателя степени говорит только о порядке числа, но не о том, является ли оно отрицательным или положительным. Вот как выражаются отрицательные числа в научной нотации:
–5,8125 × 107 соответствует –58 125 000;
–5,8125 × 10–7 соответствует –0,00000058125.
В компьютерах вместо формата с фиксированной точкой используется формат с плавающей точкой, который идеально подходит для хранения малых и больших значений, поскольку основан на научной нотации. Однако применяемый в компьютерах формат с плавающей точкой подразумевает запись в научной нотации двоичных чисел, поэтому нам необходимо выяснить, как выглядят дробные числа в двоичном формате.
Все гораздо проще, чем может показаться. В десятичной записи числа цифры справа от десятичного разделителя соответствуют отрицательным степеням числа 10. В двоичной записи цифры справа от двоичного разделителя (который выглядит так же, как и десятичный) соответствуют отрицательным степеням числа 2. Давайте преобразуем двоичное число в десятичное.
101,1101 1 × 4 +
0 × 2 +
1 × 1 +
1 ÷ 2 +
1 : 4 +
0 : 8 +
1 : 16
Операции деления можно заменить умножением на отрицательные степени числа 2:
1 × 22 +
0 × 21 +
1 × 20 +
1 × 2–1 +
1 × 2–2 +
0 × 2–3 +
1 × 2–4.
Отрицательные степени числа 2 можно также рассчитать путем последовательного деления 1 на 2:
1 × 4 +
0 × 2 +
1 × 1 +
1 × 0,5 +
1 × 0,25 +
0 × 0,125 +
1 × 0,0625.
В результате этого вычисления находим, что десятичный эквивалент двоичного числа 101,1101 равен 5,8125.
В десятичной научной нотации нормализованная значащая часть числа должна быть больше или равна 1, но меньше 10. Таким же образом в двоичной научной нотации нормализованная значащая часть числа должна быть больше либо равна 1, но меньше числа 10, которое соответствует 2 в десятичной системе счисления. Выразим число в двоичной научной нотации.
101,1101 1,011101 × 22
Интересное следствие этого правила: слева от двоичного разделителя в нормализованном двоичном числе с плавающей точкой может стоять только 1.
У большинства современных компьютеров и программ, использующих числа с плавающей точкой, применяется стандарт, введенный в 1985 году Институтом инженеров электротехники и электроники (Institute of Electrical and Electronics Engineers, IEEE) и признанный Американским национальным институтом стандартов (American National Standards Institute, ANSI), — ANSI/IEEE Std 754–1985, стандарт IEEE для двоичной арифметики с плавающей точкой. В кратком описании этого стандарта, занимающем всего 18 страниц, хорошо изложены основы кодирования двоичных чисел с плавающей точкой.
Стандарт IEEE предусматривает два основных формата: число одинарной точности, занимающее в памяти четыре байта, и число двойной точности, занимающее восемь байт.
Сначала рассмотрим число одинарной точности. Оно состоит из трех частей: один бит отводится для знака (0 используется для положительного числа, а 1 — для отрицательного), восемь бит — для порядка, а 23 бита — для дробной значащей части числа, в которой самый младший бит — крайний справа.
1 знаковый бит (s)
8 битов порядка (e)
23 бита дробной значащей части (f)
Итого 32 бита, или четыре байта. Поскольку в значащей части нормализованного двоичного числа с плавающей точкой слева от двоичного разделителя всегда стоит 1, соответствующий ей бит не включается при сохранении числа в формате IEEE. Сохраняется только 23-битная дробная часть. Несмотря на то что для хранения значащей части числа используется только 23 бита, считается, что точность равна 24 битам. Чуть позже мы разберемся в том, что это значит.
Значение 8-битного порядка находится в диапазоне от 0 до 255. Такой порядок называется смещенным. Для нахождения истинного значения порядка с учетом знака необходимо вычесть из него число, называемое смещением. Для чисел одинарной точности с плавающей точкой смещение порядка равно 127.
Значения порядка 0 и 255 используются в особых случаях, о которых расскажу чуть позже. Если значение порядка принадлежит диапазону от 1 до 254, то число, представленное конкретными значениями s (бит знака), e (порядок) и f (дробная часть), равно:
(–1)s × 1,f × 2е − 127.
Выражение (–1)s используется для определения знака числа. Если s равно 0, то число положительное (поскольку любое число в степени 0 равно 1), если s равно 1, то число отрицательное (поскольку –1 в степени 1 равно –1).
Следующая часть выражения 1,f представляет 1, за которой следует двоичный разделитель и 23-битная дробная значащая часть. Все это умножается на 2, возведенное в степень, значением которой является разность хранящегося в памяти 8-битного смещенного порядка и числа 127.
Я не упомянул о способе выражения такого распространенного числа, как 0. Похоже, о нем мы и забыли. Для этого предусмотрено несколько особых случаев:
если e равно 0, f равно 0, то число равно 0; как правило, для представления числа 0 во все 32 бита записываются нули, однако бит знака может быть равен 1, и в этом случае число интерпретируется как отрицательный ноль; бит может обозначать очень маленькое отрицательное число, для представления которого с одинарной точностью доступных цифр и порядков недостаточно;
если e равно 0, а f не равно 0, то число является действительным, но не нормализованным:
(–1)s × 0,f × 2–127;
обратите внимание на 0 слева от двоичного разделителя значащей части;
если e равно 255, а f равно 0, то число символизирует положительную или отрицательную бесконечность — в зависимости от знака s;
если e равно 255, а f не равно 0, то значение считается «не числом» и обозначается аббревиатурой NaN (Not a Number — «не число»); NaN может указывать на неизвестное число или на результат недопустимой математической операции.
Наименьшее нормализованное положительное или отрицательное двоичное число, которое можно представить с одинарной точностью в формате с плавающей точкой, следующее:
1,00000000000000000000000ДВА × 2–126.
В этом числе после двоичного разделителя следуют 23 двоичных нуля. Наибольшее нормализованное положительное или отрицательное двоичное число, которое можно представить с одинарной точностью в формате с плавающей точкой, следующее:
1,11111111111111111111111ДВА × 2127.
В десятичной системе счисления эти два числа приблизительно равны 1,175494351 × 10–38 и 3,402823466 × 1038. Именно этими числами ограничивается диапазон чисел с плавающей точкой одинарной точности.
Вероятно, вы помните, что десять двоичных цифр примерно эквивалентны трем десятичным цифрам. Под этим подразумеваю, что двоичное число, состоящее из десяти единиц, которое соответствует числу 3FFh в шестнадцатеричном формате и 1023 в десятичном, приблизительно равно числу из трех девяток, то есть 999. Таким образом:
210 ≈ 103.
Из этого соотношения следует, что 24-битное двоичное число одинарной точности в формате с плавающей точкой приблизительно эквивалентно десятичному числу, состоящему из семи цифр. По этой причине считается, что число одинарной точности в формате с плавающей точкой имеет точность до 24 битов, или около семи десятичных знаков. Что это значит?
Точность числа с фиксированной точкой очевидна. Например, денежная сумма, выраженная в виде числа с фиксированной точкой, имеющего два десятичных знака, определена с точностью до цента. Однако о числах с плавающей точкой мы не можем сказать ничего подобного. В зависимости от значения порядка число с плавающей точкой может иметь точность до долей цента или до десятков долларов.
Правильнее было бы сказать, что число одинарной точности с плавающей точкой имеет точность до одной части из 224 (одной части из 16 777 216, примерно до шести частей из 100 миллионов). Что это значит на самом деле?
Во-первых, если вы попытаетесь выразить значения 16 777 216 и 16 777 217 в виде чисел одинарной точности с плавающей точкой, они окажутся одинаковыми. Более того, любое число в промежутке между этими двумя значениями (например, 16 777 216,5) тоже будет совпадать с ними. Все три десятичных числа сохраняются в памяти в виде 32-битного числа одинарной точности с плавающей точкой, которое, будучи разделенным на биты знака, порядка и значащей части, выглядит следующим образом.
4B800000h
0 10010111 00000000000000000000000
И оно эквивалентно
1,00000000000000000000000ДВА × 224.
Следующее значение, выраженное двоичным числом с плавающей точкой, эквивалентно числу 16 777 218:
1,00000000000000000000001ДВА × 224.
Хранение двух разных десятичных значений в виде одинаковых чисел с плавающей точкой не всегда создает проблемы.
Правда, если при написании банковской программы вы используете числа одинарной точности с плавающей точкой для хранения денежных сумм в долларах и центах, вас, вероятно, будет беспокоить то, что 262 144,00 доллара равны 262 144,01 доллара. Обе эти суммы выражаются числом:
1,00000000000000000000000ДВА × 218.
Это одна из причин, почему при работе с долларами и центами предпочтительнее применять формат с фиксированной точкой. При использовании чисел с плавающей точкой вы можете обнаружить и другие раздражающие нюансы. Например, программа, выполняющая вычисление, в результате которого должно получиться число 3,50, выдает значение 3,499999999999. Так часто бывает при использовании чисел с плавающей точкой, и с этим ничего нельзя поделать.
Если вы твердо решили остановиться на числах с плавающей точкой, но вам недостаточно одинарной точности, попробуйте применить числа с плавающей точкой двойной точности. Числа в этом формате занимают восемь байт памяти, распределенных следующим образом.
1 знаковый бит (s)
11 бит порядка (e)
52 бита дробной значащей части (f)
Смещение порядка равно 1023, или 3FFh, поэтому число в этом формате записывается так:
(–1)s × 1,f × 2е − 1023.
К нулю, бесконечности и значениям NaN применяются правила, аналогичные тем, которые мы рассматривали, когда говорили о числах одинарной точности.
Наименьшее положительное или отрицательное число двойной точности с плавающей точкой следующее:
1,0000000000000000000000000000000000000000000000000000ДВА × 2–1022.
В этом числе после двоичного разделителя следуют 52 нуля. Наибольшее число:
1,1111111111111111111111111111111111111111111111111111ДВА × 21023.
Соответствующие десятичные числа формируют диапазон примерно от 2,2250738585072014 × 10–308 до 1,7976931348623158 × 10308. Число 10308 очень велико, оно представляет единицу с 308 нулями.
Пятидесятитрехбитная значащая часть числа (включая первый неучитываемый бит) приблизительно эквивалентна 16 десятичным знакам. Это уже намного лучше формата с одинарной точностью, однако вероятность того, что какое-то число однажды станет равно другому, по-прежнему существует. Возьмем, к примеру, числа 140 737 488 355 328,00 и 140 737 488 355 328,01. Они оба будут храниться в виде 64-битного числа двойной точности с плавающей точкой:
42E0000000000000h.
В двоичном формате это число выглядит так:
1,0000000000000000000000000000000000000000000000000000ДВА × 247.
Разумеется, разработка формата для хранения в памяти чисел с плавающей точкой является лишь небольшим этапом в процессе фактического использования этих чисел в программах, написанных на языке ассемблера. Если бы вы конструировали компьютер с нуля, сейчас бы возникла проблема создания набора функций для сложения, вычитания, умножения и деления чисел с плавающей точкой. К счастью, эти задачи можно разбить на более мелкие подзадачи, связанные со сложением, вычитанием, умножением и делением целых чисел, решать которые вы уже научились.
Например, сложение чисел с плавающей точкой сводится к сложению их значащих частей; сложность заключается лишь в порядках. Предположим, вам необходимо выполнить следующую операцию сложения:
(1,1101 × 25) + (1,0010 × 22).
В данном случае нужно сложить числа 11101 и 10010, однако второе число необходимо преобразовать с учетом разницы в значениях порядков. Фактически требуется сложить целые числа 11101000 и 10010. Итоговая сумма составит:
1,1111010 × 25.
Иногда разница в порядках может быть такой большой, что одно из двух чисел даже не повлияет на сумму. Это может произойти, например, при сложении расстояния от Земли до Солнца и радиуса атома водорода.
Перемножение двух чисел с плавающей точкой сводится к перемножению двух значащих частей как обычных целых чисел и сложению двух целочисленных значений порядков. Нормализация значащей части может привести к уменьшению нового значения порядка.
Следующий уровень сложности при использовании чисел с плавающей точкой связан с вычислением квадратных корней, степеней, логарифмов и тригонометрических функций. Однако все эти задачи можно решить с помощью четырех основных операций: сложения, вычитания, умножения и деления.
Например, такая тригонометрическая функция, как синус, вычисляется с помощью разложения в ряд.
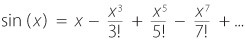
Аргумент x должен выражаться в радианах, где 360° — это 2π радиан, восклицательный знак — факториал числа, или произведение всех целых чисел от 1 и до этого числа. Например, 5! = 1 × 2 × 3 × 4 × 5. В данном случае все сводится к простому умножению. Возведение числителей дробей в степень тоже предполагает умножение. Остальными операциями являются деление, сложение и вычитание. Единственная по-настоящему сложная часть — многоточие в конце выражения, означающее, что это вычисление может продолжаться бесконечно. На практике если вы ограничитесь диапазоном от 0 до π/2 (из которого можно вывести все остальные значения синуса), то сможете избежать лишних вычислений. Вам достаточно десятка слагаемых в этом разложении для получения 53-битных значений двойной точности.
Если учесть, что компьютеры предназначены для того, чтобы облегчать людям жизнь, может показаться, что написание множества подпрограмм для выполнения арифметических операций с плавающей точкой противоречит цели их создания. Однако в этом вся прелесть программного обеспечения. Написанные кем-то подпрограммы для конкретного компьютера могут использоваться другими людьми. Арифметика с плавающей точкой настолько важна для научных и инженерных приложений, что ей традиционно придается огромное значение. На заре компьютерной эры при создании программного обеспечения для нового типа компьютеров написание подпрограмм для выполнения расчетов с плавающей точкой было одной из первоочередных задач.
Целесообразно разработать машинные инструкции специально для выполнения вычислений с плавающей точкой! Очевидно, это легче сказать, чем сделать, однако важность такой задачи трудно переоценить. Если вы сможете реализовать арифметику с плавающей точкой на уровне аппаратного обеспечения, подобно командам умножения и деления в 16-разрядных микропроцессорах, то все вычисления с плавающей точкой будут выполняться компьютером гораздо быстрее.
Первым коммерческим компьютером, в котором вычисления с плавающей точкой могли осуществляться на аппаратном уровне, был IBM 704, выпущенный в 1954 году. Все числа в нем хранились в виде 36-битных значений. Числа с плавающей точкой разбивались на 27-битную значащую часть, 8-битный порядок и однобитный знак. Специальные аппаратные компоненты для расчетов с плавающей точкой могли выполнять операции сложения, вычитания, умножения и деления. Остальные функции реализовывались в программном обеспечении.
В настольном компьютере аппаратное обеспечение для вычислений с плавающей точкой появилось в 1980 году, когда компания Intel выпустила чип 8087. Интегральные микросхемы такого типа в наши дни называются математическими сопроцессорами, или блоками вычислений с плавающей точкой. Микросхема 8087 была названа сопроцессором, поскольку не могла работать сама по себе. Ее можно было использовать только в сочетании с первыми 16-разрядными микропроцессорами Intel 8086 и 8088.
Сопроцессор 8087 — микросхема с 40 выводами, которая использует многие из тех же сигналов, что и микропроцессоры 8086 и 8088. С помощью этих сигналов микропроцессор и математический сопроцессор взаимодействуют. Когда ЦПУ считывает специальную команду ESC (Escape), сопроцессор перехватывает управление и выполняет следующий машинный код, соответствующий одной из 68 команд для вычисления тригонометрических функций, степеней, логарифмов и т. д. Типы данных основаны на стандарте IEEE. В свое время сопроцессор 8087 считался самой сложной интегральной схемой.
Сопроцессор можно назвать небольшим автономным компьютером. В ответ на получение конкретной машинной инструкции для выполнения операции с плавающей точкой (например, команды FSQRT для вычисления квадратного корня) сопроцессор выполняет собственную последовательность команд, сохраненных в ПЗУ. Эти внутренние команды называются микрокодом. Как правило, эти вычисления осуществляются с помощью цикла, поэтому их результат предоставляется не сразу. Тем не менее математический сопроцессор обычно решает задачи по меньшей мере в десять раз быстрее, чем эквивалентные процедуры, реализованные в виде ПО.
Материнская плата первого компьютера IBM PC предусматривала 40-контактное гнездо для микросхемы 8087 рядом с процессором 8088. К сожалению, это гнездо было пустым. Пользователям, которым требовалось ускорить операции с плавающей точкой, приходилось приобретать микросхему 8087 отдельно и самостоятельно устанавливать ее. Однако даже после установки математического сопроцессора не все приложения начинали работать быстрее. Некоторые программы, например текстовые редакторы, практически не нуждаются в вычислениях с плавающей точкой. Другие программы, вроде электронных таблиц, могут выполнять подобные вычисления гораздо чаще, поэтому они должны работать быстрее, однако от использования этой микросхемы скорость работы увеличивалась далеко не у всех приложений.
Дело в том, что программистам нужно было писать специальный код для использования машинных инструкций сопроцессора. Поскольку математический сопроцессор не являлся стандартным компонентом аппаратного обеспечения, многие себя этим не утруждали. В конце концов им все равно приходилось писать собственные подпрограммы для вычислений с плавающей точкой (поскольку у большинства пользователей не было математического сопроцессора), поэтому микросхема 8087 не освободила их от лишней работы, а наоборот, выявила дополнительные задачи. Со временем программисты научились писать приложения для использования математического сопроцессора, если он входил в состав компьютера, и эмулировать его работу, если не входил.
В дальнейшем компания Intel также выпустила математические сопроцессоры 287 и 387 для микропроцессоров 286 и 386 соответственно. В 1989 году появился процессор Intel 486DX, в который сопроцессор был встроен. С тех пор он перестал быть дополнительным компонентом. К сожалению, в 1991 году Intel сконструировала более дешевый микропроцессор 486SX без встроенного сопроцессора, а также отдельный математический сопроцессор 487SX. Однако с изготовлением процессора Pentium в 1993 году встроенный сопроцессор снова стал стандартом, вероятно навсегда. Компания Motorola интегрировала сопроцессор в микросхему 68040 в 1990 году. До этого Motorola продавала математические сопроцессоры 68881 и 68882 для изготовленных ранее микропроцессоров семейства 68000. Микросхемы PowerPC также предусматривают встроенный сопроцессор для выполнения вычислений с плавающей точкой.
Несмотря на то что аппаратный компонент для операций с плавающей точкой — подспорье для ассемблерного программиста, это устройство кажется малозначимой вехой в истории развития вычислительной техники, особенно если сравнивать с другими разработками, начатыми в 1950-х годах. Далее мы поговорим о языках программирования.

