Глава 9
За битом бит

Когда в 1973 году Тони Орландо в своей песне попросил, чтобы любимая «повязала желтую ленточку вокруг старого дуба», он не сопроводил свою просьбу ни подробными объяснениями, ни долгими рассуждениями. Никаких «если», «и», «но». Несмотря на сложные чувства и эмоции, сопровождавшие ситуацию, что разворачивалась в реальной жизни и легла в основу песни, мужчине хотелось получить простой ответ: «да» или «нет». Он знал, что, если на старом дубе появится желтая ленточка, это будет означать: «Да, хотя ты и наворотил дел и провел три года в тюрьме, я все равно хочу, чтобы ты вернулся и мы жили под одной крышей». А отсутствие желтой ленточки скажет: «Даже не думай здесь останавливаться».

Здесь есть две четкие взаимоисключающие альтернативы. Тони Орландо не пел: «Повяжи половину желтой ленточки, если тебе нужно время на размышление» или «Повяжи голубую ленточку, если больше не любишь меня, но по-прежнему хочешь остаться друзьями». Нет, он все сформулировал очень просто.

Не менее информативно, нежели отсутствие или наличие желтой ленточки (разве что не столь поэтично), сработал бы дорожный знак, поставленный во дворе, например «Путь открыт» или «Въезд запрещен». Или табличка на двери «Закрыто» или «Открыто». Или фонарик на окне — включенный или выключенный.

Если вам нужно просто сказать «да» или «нет», то способов хватает. Для этого не надо произносить ни одной фразы, слова, даже буквы. Необходим всего один бит, то есть 0 или 1.

Как мы узнали в предыдущих главах, десятеричная система, которой мы пользуемся при подсчете предметов, на самом деле ничем не примечательна. Ясно, что мы пользуемся системой с основанием 10, так как у нас 10 пальцев на руках. Мы могли бы с тем же успехом использовать систему с основанием 8 (будь мы мультяшками), 4 (будь мы омарами) или даже 2 (если бы мы были дельфинами).

Однако двоичная система счисления все-таки особенная. Дело в том, что это простейшая возможная система счисления. В двоичной системе всего две цифры: 0 и 1. Если нам нужно что-то проще двоичной системы, придется избавиться от 1, и останется только 0. Имея всего лишь 0, ничего не сделаешь.

Слово «бит» — сокращение от английского выражения binary digit («двоичная цифра»). Пожалуй, это одно из симпатичнейших слов в компьютерной терминологии. В английском языке у слова bit есть и общеупотребительное значение — «кусочек, небольшая часть», и это значение нам отлично подходит, поскольку один бит — двоичная цифра, мельчайший фрагмент информации.

Иногда, если изобретается новое слово, ему присваивается новое значение. В данном случае все именно так. Слово «бит» — это не только двоичные цифры, при помощи которых удобно считать дельфинам. В компьютерную эпоху это слово приобрело значение «мельчайший первичный фрагмент информации».

Да, смелое утверждение. Естественно, информация передается не только при помощи битов. Буквы, слова, азбука Морзе и шрифт Брайля, а также десятеричные цифры тоже переносят информацию. Суть бита заключается в том, что он передает очень мало информации. Один бит — это минимально возможное количество информации. Меньше бита — отсутствие информации.

Поскольку бит выражает минимальный возможный объем информации, более сложную информацию можно передать некоторым количеством битов. (Говоря, что бит передает мало информации, я совершенно не имею в виду, что эта информация граничит с бессмыслицей. Желтая ленточка очень важна для тех, кто в ней заинтересован.)

«Запомните, дети, — слышал весь мир, // Как в полночь глухую скакал Поль Ревир…» — писал Генри Лонгфелло. Возможно, он исторически недостоверно описал поступок Поля Ревира, предупредившего американских колонистов о вторжении британцев, однако эти стихи замечательно демонстрируют, как можно передать важную информацию при помощи битов.

Он другу сказал: «Я сигнала жду.
Коль ночью из города наступать
Начнут британцы, ты дай мне знать,
На Северной церкви зажги звезду, —
Одну, если сушей, а морем — две».

Итак, Ревир дал другу два фонаря. Если британцы вторгнутся по суше, друг зажжет на колокольне один, если высадятся с моря — то зажжет оба.

Правда, Лонгфелло не дает явного указания на все случаи жизни. Он умалчивает о третьей возможности, означающей, что британцы пока не вторгаются. Лонгфелло подразумевает, что тогда ни одного фонаря на колокольне гореть не будет.

Допустим, два фонаря висят на колокольне всегда. Как правило, они не горят.

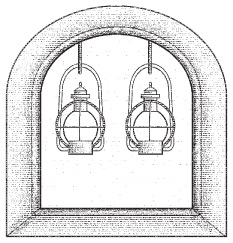
Значит, британцы пока не наступают. Если зажжен один фонарь, значит, британцы наступают по суше, если горят оба, — высаживаются с моря.

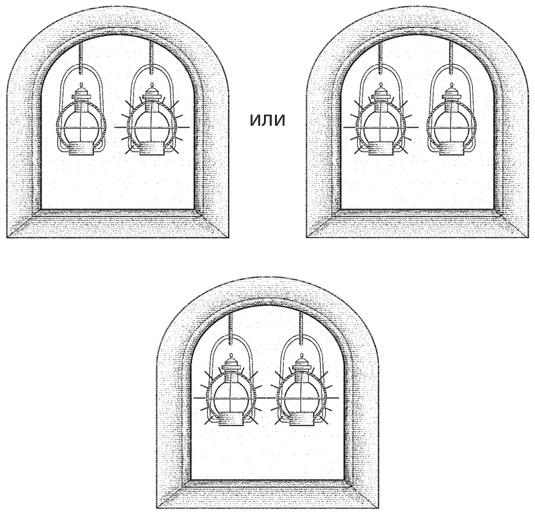
Каждый фонарь — это один бит. Зажженный фонарь равен единичному биту, незажженный — нулевому биту. Тони Орландо показал, что для описания любой из двух возможностей достаточно всего одного бита. Если бы Поль Ревир должен был оповестить людей лишь о том, вторгаются британцы или нет (а не откуда именно), то хватило бы и одного фонаря. Фонарь горел бы в случае нападения и был бы потушен, если бы предстоял еще один спокойный вечер.

Чтобы описать одну из трех возможностей, требуется два фонаря. При наличии второго фонаря и двух битов уже можно описать четыре возможности:

00 = британцы пока не наступают;

01 = британцы наступают с суши;

10 = британцы наступают с суши;

11 = британцы наступают с моря.

На самом деле Поль Ревир, ограничившись всего тремя возможностями, поступил весьма хитроумно. В телекоммуникационной терминологии можно сказать, что он задействовал избыточность, позволяющую бороться с шумом. Термин «шум» в теории телекоммуникаций означает любые помехи, осложняющие передачу информации. Типичный пример шума — помехи на телефонной линии. Тем не менее, даже несмотря на помехи, общение по телефону обычно проходит успешно, поскольку устная речь крайне избыточна. Не требуется четко слышать каждый слог в каждом слове, чтобы понять, что сказали.

В случае с фонарями на колокольне к «шуму» можно отнести такие факторы, как темнота и расстояние от Поля Ревира до колокольни, которые могут помешать отличить первый фонарь от второго. Вот важнейший отрывок из стихов Лонгфелло:

Вдруг видит — звездой огонек замигал,

То дан с колокольни желанный сигнал!

В седло он вскочил, сжал повод в ладонь.

Под ним захрапел в нетерпенье конь.

Второй сигнал! Он коня погнал!

Скорее всего, Поль Ревир был не в состоянии определить, какой фонарь зажегся первым.

Из этого следует важный вывод: информация — выбор из двух или более возможностей. Например, когда мы говорим с кем-либо, любое произносимое слово выбирается из словаря. Если бы мы пронумеровали все слова из словаря от 1 до 351 482, то могли бы столь же четко вести беседу, называя номера, а не слова (естественно, обоим собеседникам понадобились бы словари, где все слова пронумерованы одинаково, а также терпение).

Верно и обратное: любую информацию можно свести к выбору между двумя или более возможностями, а сами возможности выразить при помощи битов. Излишне говорить, что существует множество таких вариантов человеческой коммуникации, где выбор между конкретными возможностями не предоставляется, и такие формы коммуникации также жизненно необходимы. Вот почему люди не флиртуют с компьютерами (по крайней мере, хочется на это надеяться). Если некоторую информацию невозможно выразить при помощи слов, картинок или звуков, значит, ее нельзя закодировать при помощи битов. Да и не возникает такого желания.

Жесты «палец вверх» или «палец вниз» содержат по одному биту информации. Еще есть жесты «два пальца вверх» и «два пальца вниз». Два последних жеста нравились ныне покойным кинокритикам Роджеру Эберту и Джину Сискелу, которые таким образом выносили окончательные вердикты по новейшим фильмам. Итак, в данном случае мы следим только за их большими пальцами. Получается четыре возможности, которые можно представить в виде двух битов:

00 = обоим не понравилось;

01 = Сискелу не понравилось, Эберту понравилось;

10 = Сискелу понравилось, Эберту не понравилось;

11 = обоим понравилось.

Первый бит относится к Сискелу; таким образом, 0 означает, что кино не понравилось Сискелу, а 1 — что кино понравилось Сискелу. Аналогично второй бит описывает вкусы Эберта. Итак, если друг спросит, что решили Сискел и Эберт о фильме Impolite Encounter, вы, вместо того чтобы ответить: «С точки зрения Сискела — большой палец вверх, с точки зрения Эберта — большой палец вниз» или «Сискелу понравилось; Эберту — нет», можете просто сказать: «Один ноль». Если друг знает, какой бит относится к Сискелу, а какой — к Эберту, а 1 означает «палец вверх», 0 — «палец вниз», то ваш ответ будет понятен. Просто вы должны знать код.

Можно сразу условиться, что бит 1 означает «палец вниз», а 0 — «палец вверх». Это может показаться нелогичным. Естественно, мы привыкли считать, что 1 означает нечто «утвердительное», а 0 — наоборот. На самом деле такое соответствие произвольное. Требуется всего лишь, чтобы все, кто пользуется кодом, знали значения бита 0 и 1.

Значение конкретного бита или совокупности битов всегда понимается в контексте. Вероятно, смысл желтой ленточки, повязанной на конкретном дубе, понятен лишь тому, кто ее туда повесил, и тому, для кого предназначен этот знак. Достаточно изменить цвет, дерево, дату — и значение исчезнет, останется просто тряпочка. Чтобы извлечь какую-либо полезную информацию из жестикуляции Сискела и Эберта, нужно как минимум понимать, о каком фильме идет речь.

Если вы вели список фильмов, отрецензированных Сискелом и Эбертом, и фиксировали их голоса, можно добавить в систему еще один бит, который будет выражать ваше мнение. В таком случае количество возможностей доходит до восьми:

000 = Сискелу не понравилось; Эберту не понравилось; мне не понравилось;

001 = Сискелу не понравилось; Эберту не понравилось; мне понравилось;

010 = Сискелу не понравилось; Эберту понравилось; мне не понравилось;

011 = Сискелу не понравилось; Эберту понравилось; мне понравилось;

100 = Сискелу понравилось; Эберту не понравилось; мне не понравилось;

101 = Сискелу понравилось; Эберту не понравилось; мне понравилось;

110 = Сискелу понравилось; Эберту понравилось; мне не понравилось;

111 = Сискелу понравилось; Эберту понравилось; мне понравилось.

Один из плюсов при представлении этой информации в виде битов таков: мы уверены, что учли все возможности, мы знаем, что существует восемь и только восемь возможностей — ни больше, ни меньше. Имея три бита, можно сосчитать лишь от нуля до семи. Трехзначных двоичных чисел больше нет.

Итак, при описании таких битов Сискела и Эберта вас, возможно, уже занимает следующий непростой вопрос: «А что насчет сборника рецензий Leonard Maltin’s Movie & Video Guide?» Ведь Леонард Малтин оценивает фильмы не такими «пальцевыми» жестами, а более традиционно — при помощи системы звезд.

Чтобы определить, сколько битов Малтина требуется, сперва необходимо разобраться в его системе. Малтин оценивает фильм в некоторое количество звезд (от одной до четырех), причем звезда может делиться и пополам. (Кстати, одну звезду Мартин никогда не присваивает; вместо этого такой фильм получает рейтинг КРАХ.) Вот семь возможностей, и это означает, что для представления любой оценки достаточно трех бит:

«Что же насчет 111?» — могли бы спросить вы. Да, этот код ничего не значит. Он не определен. Если бы мы использовали двоичный код 111 в рейтингах Малтина, это бы свидетельствовало об ошибке. (Вероятно, ошибся компьютер, ведь люди никогда не ошибаются!)

Напомню, что, когда мы представляли оценки Сискела и Эберта при помощи двух битов, левый бит относился к Сискелу, правый — к Эберту. Есть ли в данном случае какое-либо значение у отдельных битов? Да, в некотором роде. Если взять числовое значение такого битового кода, прибавить к нему 2, а затем разделить результат на 2, то получится количество звезд. Это возможно лишь потому, что мы определяли коды продуманно и непротиворечиво. Мы вполне могли определить коды и так:

Этот код столь же адекватен, как и предыдущий, если всем понятно его значение.

Если бы Малтину попался фильм, не заслуживающий даже единственной звезды, он мог бы присвоить ему рейтинг в половину звезды. Определенно, кодов на это ему бы хватило. В таком случае коды следовало бы перераспределить так:

Однако если бы затем нашелся такой провальный фильм, который даже половины звезды не заслуживает (МЕГАКРАХ?), то понадобился бы еще один бит: 3-битных кодов больше не осталось.

В журнале Entertainment Weekly оцениваются не только фильмы, но и телешоу, CD, книги, сайты. Оценки варьируются от A+ до F (правда, есть ощущение, что такой чести удостаиваются лишь фильмы Поли Шора). Если подсчитать все возможные оценки, их наберется тринадцать. Для представления этой системы понадобится четыре бита:

0000 = F;

0001 = D–;

0010 = D;

0011 = D+;

0100 = C–;

0101 = С;

0110 = C+;

0111 = B–;

1000 = B;

1001 = B+;

1010 = A–;

1011 = A;

1100 = A+.

У нас осталось три неиспользованных кода: 1101, 1110 и 1111, а всего их шестнадцать.

Рассуждая о битах, мы часто говорим о конкретном числе битов. Чем больше битов у нас в распоряжении, тем больше возможностей удается с их помощью описать.

Естественно, с десятеричными числами складывается точно такая же ситуация. Например, сколько всего региональных телефонных кодов? Региональный телефонный код в США состоит из трех цифр. Если все эти коды будут задействованы (на самом деле пока не все, но мы это проигнорируем), получится 103, или 1000 таких кодов, — от 000 до 999. Сколько семизначных телефонных кодов может быть в зоне действия регионального кода 212? 107, или 10 000 000. Сколько телефонных номеров может быть в зоне действия регионального кода 212, причем с префиксом 260? 104, или 10 000.

Аналогично в двоичной системе количество возможных кодов всегда равно двойке в некоторой степени, где степень — количество битов.

Количество битов

Количество кодов

21 = 2

22 = 4

23 = 8

24 = 16

25 = 32

26 = 64

27 = 128

28 = 256

29 = 512

210 = 1024

Каждый дополнительный бит удваивает количество кодов.

Если известно, сколько нужно кодов, можно ли рассчитать, сколько для этого потребуется битов? Иными словами, как считать в противоположном направлении по вышеприведенной таблице?

Используемый при этом метод иногда называется «логарифм по основанию два». Логарифм — феномен, противоположный возведению в степень. Известно, что 2 в седьмой степени равно 128. Логарифм 128 по основанию 2 равен 7. В более строгой математической нотации получается, что выражение

27 = 128

эквивалентно выражению

log2128 = 7.

Итак, если логарифм 128 по основанию 2 равен 7, а логарифм 256 по основанию 2 равен 8, то каков логарифм 200 по основанию 2? На самом деле он равен примерно 7,64, но нам этого знать и не требуется.

Как правило, биты скрыты от поверхностного взгляда в глубинах электронных устройств. Вы не увидите их на компакт-диске, в электронных часах или внутри компьютера. Лишь иногда биты различимы вполне отчетливо.

Приведу пример. Если у вас есть обычный фотоаппарат с 35-миллиметровой пленкой, возьмите кассету и поверните ее, как показано на рисунке.

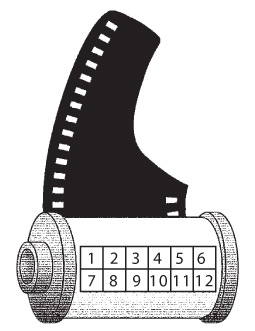
Перед вами предстанет набор серебристых и черных квадратов, отдаленно напоминающий шахматную доску. На рисунке я пронумеровал их от 1 до 12. Этот набор называется DX-кодировкой. Эти 12 квадратов в действительности представляют собой 12 бит. Серебристый квадрат соответствует 1, черный — 0. Квадраты 1 и 7 всегда серебристые (1).

Что значат эти биты? Вы, возможно, знаете, что пленки различаются по светочувствительности. Пленка высокой чувствительности считается «быстрой», поскольку на ней можно производить съемку с очень короткими экспозициями. Чувствительность пленки измеряется в единицах ASA (American Standards Association, Американская ассоциация по стандартам), причем наиболее популярны пленки с чувствительностью 100, 200 и 400 единиц. Чувствительность в единицах ASA не только напечатана на упаковке, но и закодирована на кассете.

Различают 24 стандартные степени светочувствительности для фотопленки.

100

125

160

200

250

320

400

500

640

800

1000

1250

1600

2000

2500

3200

4000

5000

Сколько битов нужно, чтобы закодировать чувствительность пленки? Ответ прост: пять. Мы знаем, что 24 = 16, а это слишком мало. А вот 25 = 32 — больше чем достаточно.

Соответствие между квадратами на кассете и чувствительностью пленки показано в таблице.

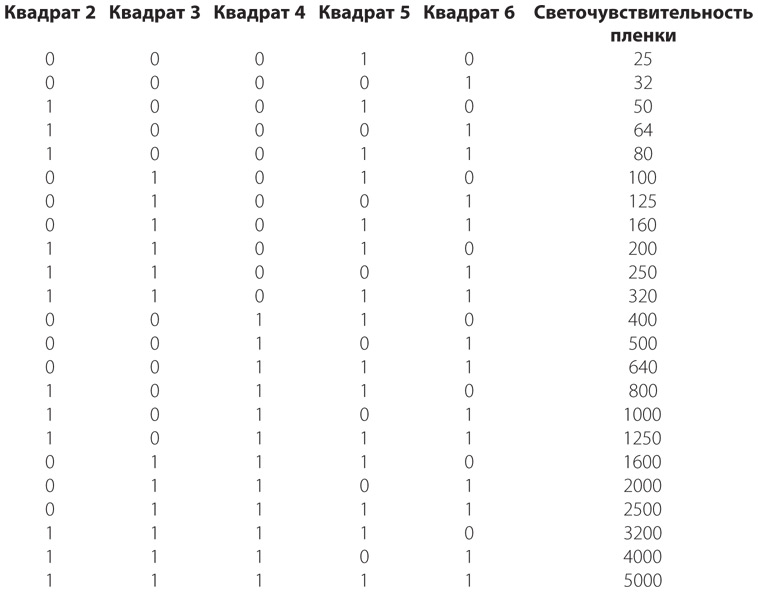
Эти коды используются в большинстве современных 35-миллиметровых фотоаппаратов. Если на вашем фотоаппарате выдержка или тип пленки устанавливаются вручную, эти коды в нем не применяются. Если же коды все-таки считываются, присмотритесь к фотоаппарату, когда будете вставлять пленку. Вы увидите шесть металлических контактов, соответствующих квадратам с первого по шестой на кассете. Серебристые квадраты — это просто открытая металлическая поверхность кассеты, которая является проводником. Черные квадраты покрыты краской, которая не проводит электричество.

Электрическая схема фотоаппарата построена так, что ток подводится к первому квадрату на кассете (он всегда серебристый). Этот ток будет (или не будет) проведен пятью контактами на квадратах со второго по шестой в зависимости от того, окрашены они изолирующей краской или нет. Так, если ток присутствует на контактах 4 и 5, но отсутствует на контактах 2, 3 и 6, в фотоаппарат вставлена пленка 400 ASA. При съемке выдержка будет установлена автоматически.

В бюджетных фотоаппаратах считываются только квадраты 0 и 3, а чувствительность пленки считается равной 50, 100, 200 или 400 единицам ASA.

Квадраты с восьмого по двенадцатый в большинстве аппаратов также не используются. В квадратах 8, 9 и 10 зашифровано число кадров на пленке, а квадраты 11 и 12 содержат сведения о том, черно-белая или цветная пленка, позитивная или негативная.

Вероятно, чаще всего вам приходилось сталкиваться с двоичными числами в коде UPC (Universal Product Code, универсальный код продукта), или просто штрихкоде, — наборе черных полос, который сегодня присутствует практически на любой упаковке. Штрихкод — наглядный символ повсеместного проникновения компьютеров в нашу жизнь.

Хотя у некоторых людей штрихкод вызывает приступы паранойи, это совершенно безобидная вещь, изобретенная для автоматизации розничной торговли и учета товаров. Со своей задачей он справляется вполне успешно. Благодаря ему, например, современные кассовые аппараты выдают покупателю чек, в котором подробно расписаны все его покупки, чего без штрихкода сделать нельзя.

Нас же в первую очередь интересует, что код UPC является двоичным, хотя на первый взгляд этого не скажешь. Давайте разберемся, как устроен штрихкод и как он работает.

Чаще всего встречается штрихкод, состоящий из нескольких цифр и 30 вертикальных полосок различной толщины, разделенных пустыми интервалами переменной толщины. В качестве примера рассмотрим штрихкод, нанесенный на банку куриного супа с вермишелью фирмы Campbell.

Сразу хочется разделить код UPC на тонкие и жирные полоски, узкие и широкие промежутки, и это действительно помогло бы разобраться в его структуре. Черные полоски и пустые промежутки штрихкода бывают различной ширины (всего четыре полоски).

Конечно, удобнее трактовать UPC как набор битов. Имейте в виду, что сканирующему устройству нет нужды просматривать штрихкод целиком, тем более прибор не может интерпретировать цифры в его основании, поскольку это потребовало бы применения сложной компьютерной технологии распознавания символов (Optical Character Recognition, OCR). Сканеру достаточно «увидеть» тонкий срез штрих-кода. Код UPC делают таким большим просто для того, чтобы кассиру легче было нацелить на него сканер. Срез, попадающий в сканер, выглядит следующим образом.

Почти как азбука Морзе, правда?

Сканируя эту информацию слева направо, компьютер присваивает бит 1 первой встреченной черной полоске и бит 0 первому промежутку. Следующие промежутки и штрихи считываются как последовательности одного, двух, трех или четырех битов в зависимости от ширины штриха или промежутка. В битовом представлении этот штрихкод выглядит так.

Итак, весь UPC — просто последовательность из 95 бит. В данном случае их можно сгруппировать.

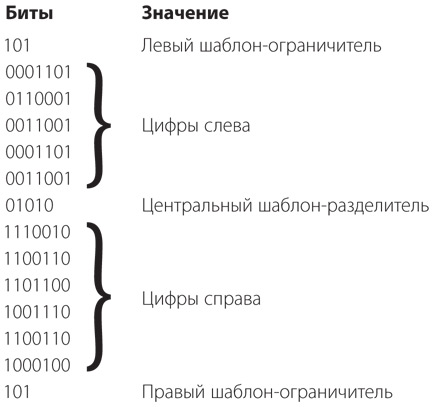
Первые три бита — всегда 101. Они называются левым шаблоном-ограничителем и нужны для того, чтобы настроить сканирующее устройство. По шаблону-ограничителю сканер определяет ширину штриха и промежутка, соответствующую одному биту. Иначе на всех упаковках код UPC пришлось бы делать одинакового размера.

За левым шаблоном-ограничителем следует шесть групп по семь бит в каждой. В них закодированы десятичные цифры от 0 до 9, в чем мы убедимся чуть позже. Затем идет 5-битовый центральный шаблон-разделитель — фиксированная группа битов (всегда 01010), используемая как встроенная контрольная система. Не найдя центрального шаблона-разделителя в нужном месте, сканер считает штрихкод неверным. В частности, так выявляют плохо пропечатанные или поддельные штрихкоды.

За центральным шаблоном-разделителем всегда идут еще шесть групп по семь бит каждая, а за ними — правый шаблон-ограничитель, всегда равный 101. Позже я расскажу, почему благодаря наличию правого шаблона-ограничителя штрихкод можно сканировать и в обратном направлении, то есть справа налево.

Всего в коде UPC зашифровано 12 десятичных цифр. Шесть из них закодированы с его левой стороны, по семь бит в каждой. Для их расшифровки применяется таблица.

Левосторонние коды

0001101 = 0

0110001 = 5

0011001 = 1

0101111 = 6

0010011 = 2

0111011 = 7

0111101 = 3

0110111 = 8

0100011 = 4

0001011 = 9

Обратите внимание: каждый 7-битовый код начинается с 0 и заканчивается 1. Встретив 7-битовый код, который начинается с 1, а заканчивается 0, сканер «понимает», что код UPC либо неверно прочитан, либо подделан. Кроме того, в каждом коде группы единиц встречаются лишь дважды. Это значит, что каждая десятичная цифра в коде UPC зашифрована двумя вертикальными штрихами.

Еще одна особенность кодов в этой таблице — нечетное количество единиц в каждом из них. Она также позволяет проверить корректность штрихкода — так называемый контроль четности (parity). Группа битов обладает четным паритетом, если в ней четное количество битов-единиц, и нечетным паритетом, если в ней нечетное количество битов-единиц.

Для расшифровки битов в правой части штрихкода применяется таблица.

Правосторонние коды

1110010 = 0

1001110 = 5

1100110 = 1

1010000 = 6

1101100 = 2

1000100 = 7

1000010 = 3

1001000 = 8

1011100 = 4

1110100 = 9

Эти коды дополняют коды из предыдущей таблицы. Там, где в левосторонних кодах был 0, теперь стоит 1, и наоборот. Правосторонние коды всегда начинаются с 1 и заканчиваются 0. Кроме того, число битов 1 в них всегда четное, что можно применять для контроля четности. Вот мы и готовы к расшифровке UPC. С помощью двух приведенных выше таблиц можно определить 11 цифр, зашифрованных на банке Campbell Soup.

0 51000 01251 7

Какая досада! Да, это те самые цифры, что напечатаны под штрихкодом. На самом деле это очень удобно: если сканер по каким-то причинам не смог прочитать код, кассир может ввести его вручную. Вы наверняка видели, как это бывает. Конечно, получается, что весь наш труд по расшифровке штрихкода был напрасным, к тому же никакой секретной информации мы так и не получили: просто 30 вертикальных штрихов превратились в 12 цифр.

Первая цифра (в данном случае 0) характеризует тип кода.

0 означает, что перед нами обычный код UPC. Если код нанесен на упаковку с товаром переменного веса, например с мясом или овощами, он начинается с 2. Товары со скидкой обозначаются цифрой 5.

Следующие пять цифр — код производителя. В нашем примере код 51000 соответствует компании Campbell Soup. Он есть на всех продуктах марки Campbell. За ними следует пятизначный (01251) код конкретного продукта этой компании, в нашем случае код банки с куриным супом. Код продукта информативен лишь в сочетании с кодом производителя. У куриного супа с вермишелью, выпущенного другой компанией, будет другой код продукта, в свою очередь код 01251 может значить нечто совершенно иное у другого производителя.

Вопреки распространенному мнению, в код UPC не включается цена товара. Информация о ней извлекается из компьютерной базы данных, используемой в кассовых аппаратах наряду со сканерами.

Последняя цифра (здесь — 7) называется символом проверки остатка и тоже используется для исключения ошибок. Чтобы проверить его на практике, присвоим букву каждой из первых 11 цифр (наш пример 0 51000 01251).

A BCDEF GHIJK

Теперь вычислим:

3 × (A + C + E + G + I + K) + (B + D + F + H + J).

Вычтем результат из ближайшего большего числа, кратного десяти. Полученное число и будет символом проверки остатка для куриного супа с вермишелью Campbell:

3 × (0 + 1 + 0 + 0 + 2 + 1) + (5 + 0 + 0 + 1 + 5) = 3 × 4 + 11 = 23.

Ближайшее большее число, кратное десяти, — 30. Значит, 30 – 23 = 7.

Это число — результат проверки остатка — напечатано под штрихкодом и зашифровано в нем. Такая проверка — одна из форм избыточности. Если остаток, вычисленный по штрихкоду, не совпадет с остатком, явно указанным в нем, штрихкод будет сочтен недействительным.

Как правило, для представления десятичной цифры от 0 до 9 достаточно четырех бит. В штрихкодах используется по семь бит на цифру. Целыми 95 бит закодировано всего 11 значимых десятичных цифр. Если учесть, что UPC с обеих сторон ограничен пустым пространством, эквивалентным девяти нулевым битам, получается, что во всем штрихкоде 11 цифр закодировано 113 бит, по 10 бит на цифру!

Такая избыточная надежность отчасти требуется для защиты от ошибок. Код товара был бы не слишком полезен, если бы покупатель мог в два счета подправить его фломастером.

Кроме того, UPC удобен, поскольку его можно считывать в обоих направлениях. Если в первых считанных цифрах количество единиц четно, сканер распознает, что код читается справа налево. Для расшифровки правосторонних цифр компьютер использует следующую таблицу.

Правосторонние коды в обратном направлении

0100111 = 0

0111001 = 5

0110011 = 1

0000101 = 6

0011011 = 2

0010001 = 7

0100001 = 3

0001001 = 8

0011101 = 4

0010111 = 9

Вот таблица левосторонних кодов.

Левосторонние коды в обратном направлении

1011000 = 0

1000110 = 5

1001100 = 1

1111010 = 6

1100100 = 2

1101110 = 7

1011110 = 3

1110110 = 8

1100010 = 4

1101000 = 9

Эти 7-битовые коды отличаются от кодов, считываемых слева направо. Никакой путаницы не возникает.

Наше знакомство с кодами началось с азбуки Морзе, состоящей из точек, тире и промежутков между ними. Азбука Морзе, на первый взгляд, имеет мало общего с нулями и единицами, на деле же сводится именно к ним.

Вспомните устройство азбуки Морзе. Тире втрое длиннее точки. Точки и тире в пределах одной буквы разделены паузами продолжительностью в одну точку. Промежутки между буквами по длительности равны одному тире. Слова разделяются паузами в два тире.

Чтобы немного упростить анализ, допустим, что длина тире превышает длину точки не в три, а в два раза. Это означает, что точка соответствует одному единичному биту, а тире — двум единичным битам.

Паузы состоят из нулевых битов.

Вот простейшая таблица с азбукой Морзе из главы 1.

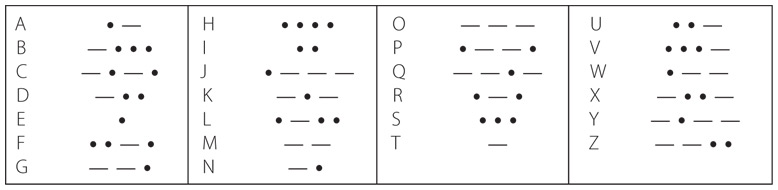
А вот та же таблица, преобразованная в биты.

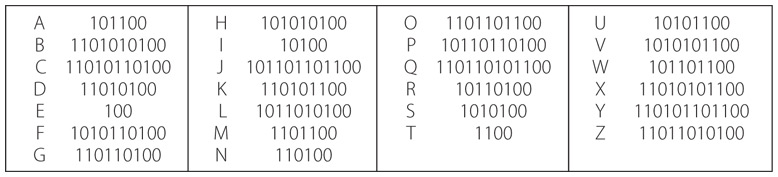
Обратите внимание: все коды начинаются с 1 и кончаются парой 0, представляющей паузу между буквами в пределах одного слова. Кодом пробела между словами является дополнительная пара 0. Таким образом, на азбуке Морзе фраза Hi there выглядит так.

Представив ее в битах, мы получим нечто очень похожее на срез штрихкода.

В битовом выражении азбука Брайля гораздо проще азбуки Морзе. Шрифт Брайля является 6-битовым кодом. Каждый символ — набор из шести точек, каждая из которых может быть выпуклой или плоской. Как говорилось в главе 3, обычно точки нумеруются от 1 до 6.

Например, вот как записывается шрифтом Брайля слово code, где крайний левый бит соответствует первой позиции, а крайний правый — шестой.

Позже мы узнаем, что с помощью битов можно зашифровать не только коды товаров, чувствительность пленки, художественную ценность фильма, способ наступления британской армии или послание любимой женщине, но и любые слова, изображения, звуки, музыку и кино. В своей основе биты — это числа. Для представления информации в форме битов достаточно пересчитать количество доступных возможностей. Это количество определяет, сколько битов понадобится для того, чтобы присвоить каждой возможности уникальный номер.

Биты также играют важную роль в логике, находящейся на стыке философии и математики; ее главная цель — определение истинности или ложности некоего утверждения. Истину и ложь также можно обозначить через 1 и 0.

Назад: Глава 8 Альтернативы десятке

Дальше: Глава 10 Логика и переключатели

Глава 9 За битом бит

Глава 9
За битом бит