Пространственно-временно́й континуум

«Французская революция началась в Париже 14 июля 1789 года». В этом предложении установлены место и время события. Тому, кто слышит это утверждение впервые и кто не знает, что значит «Париж», можно было бы сказать: это – город на нашей Земле, расположенный на 2° восточной долготы и 49° северной широты. Два числа характеризовали бы тогда место, а «14 июля 1789 года» – время, в которое произошло событие. В физике точная характеристика, когда и где произошло событие, чрезвычайно важна, гораздо важнее, чем в истории, так как эти числа образуют основу количественного описания.

Ради простоты мы рассматривали прежде только движение вдоль прямой. Нашей координатной системой был твердый стержень с началом, но без конца. Сохраним это ограничение. Отметим на стержне различные точки; положение каждой из них может быть охарактеризовано только одним числом – координатой точки. Сказать, что координата точки равна 7,586 метра, означает, что ее расстояние от начала стержня равно 7,586 метра. Наоборот, если кто-то задает мне любое число и единицу измерения, я всегда могу найти точку на стержне, соответствующую этому числу. Мы видим, что каждому числу соответствует определенная точка на стержне, а каждой точке соответствует определенное число. Этот факт выражается математиками в следующем предложении: все точки стержня образуют одномерный континуум. Тогда существует точка, сколь угодно близкая к данной точке стержня. Мы можем связать две отдаленные точки на стержне рядом отрезков, расположенных один за другим, каждый из которых сколь угодно мал. Таким образом, тот факт, что отрезки, связывающие отдаленные точки, произвольно малы, является характеристикой континуума.

Возьмем другой пример. Пусть мы имеем плоскость или, если вы предпочитаете что-либо более конкретное, поверхность прямоугольного стола (рис. 59). Положение точки на этом столе можно охарактеризовать двумя числами, а не одним, как раньше. Два числа суть расстояния от двух перпендикулярных краев стола. Не одно число, а пара чисел соответствует каждой точке плоскости; каждой паре чисел соответствует определенная точка. Другими словами: плоскость есть двухмерный континуум. Тогда существуют точки, сколь угодно близкие к данной точке плоскости. Две отдаленные точки могут быть связаны кривой, разделенной на отрезки, сколь угодно малые. Таким образом, произвольная малость отрезков, последовательно укладывающихся на кривой, связывающей две отдаленные точки, каждая из которых может быть определена двумя числами, снова является характеристикой двухмерного континуума.

Рис. 59.

Еще один пример. Представим себе, что вы хотите в качестве системы координат рассматривать свою комнату. Это означает, что вы хотите любое положение тела определить относительно стен комнаты. Положение кончика лампы, если она в покое, может быть описано тремя числами: два из них определяют расстояние от двух перпендикулярных стен, а третье – расстояние от пола или потолка. Каждой точке пространства соответствуют три определенных числа; каждым трем числам соответствует определенная точка в пространстве (рис. 60). Это выражается предложением: наше пространство есть трехмерный континуум. Существуют точки, весьма близкие к каждой данной точке пространства. И опять произвольная малость отрезков линии, связывающей отдаленные точки, каждая из которых представлена тремя числами, есть характеристика трехмерного континуума.

Но все это едва ли физика. Чтобы вернуться к физике, нужно рассмотреть движение материальных частиц. Чтобы исследовать и предсказывать явления в природе, необходимо рассматривать не только место, но и время физических событий. Возьмем снова очень простой пример.

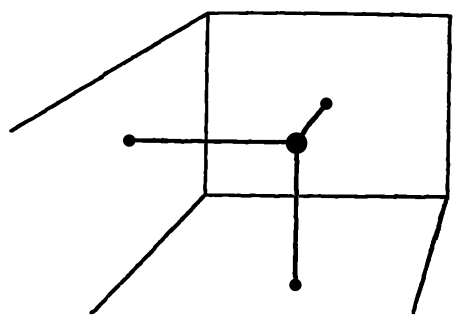
Рис. 60.

Маленький камешек, который примем за частицу, падает с башни. Допустим, что высота башни равна 80 метрам. Со времен Галилея мы в состоянии предсказать координаты камня в произвольный момент времени после начала его падения. На стр. 217 представлена «временна́я таблица», приближенно описывающая положение камня после 1, 2, 3 и 4 секунд.

В нашей «временно́й таблице» зарегистрированы пять событий, каждое из которых представлено двумя числами – временем и пространственной координатой каждого события. Первое событие есть начало движения камня с высоты 80 метров от земли в момент, равный нулю. Второе событие есть совпадение камня с нашим твердым стержнем (башней) на высоте 75 метров от земли. Это имеет место по истечении одной секунды. Последнее событие есть удар камня о землю.

Те сведения, которые записаны во «временно́й таблице», можно было бы представить иначе. Пять пар чисел ее можно было бы представить, как пять точек на плоскости. Установим сначала масштаб. Например: пусть один отрезок будет представлять метр, а другой секунду (рис. 61).

Рис. 61.

Затем нарисуем две перпендикулярные линии, одну из них, скажем, горизонтальную, назовем временно́й осью, вертикальную же – пространственной осью. Мы сразу же видим, что нашу «временну́ю таблицу» можно представить пятью точками в пространственно-временно́й плоскости (рис. 62).

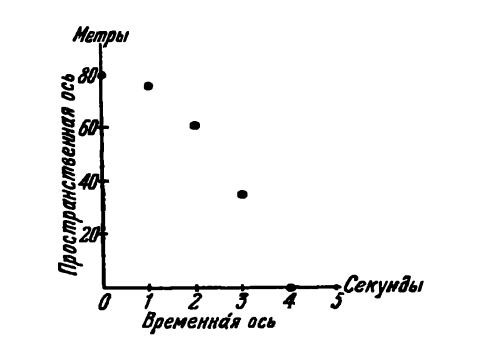
Рис. 62.

Расстояния точек от пространственной оси представляют собой координаты времени, указанные в первой колонке «временно́й таблицы», а расстояния от оси времен – их пространственные координаты.

Одна и та же связь выражена двумя способами: с помощью «временно́й таблицы» и точками на плоскости. Одно может быть построено из другого. Выбор между этими двумя представлениями является делом лишь вкуса, ибо в действительности они оба эквивалентны.

Сделаем теперь еще один шаг. Представим себе улучшенную «временну́ю таблицу», дающую положения не для каждой секунды, а, скажем, для каждой сотой или тысячной доли секунды. Тогда у нас будет много точек в нашей пространственно-временно́й плоскости. Наконец, если положение дается для каждого мгновения или, как говорят математики, если пространственная координата дается как функция времени, то совокупность точек становится непрерывной линией. Поэтому наш следующий рисунок дает не отрывочные сведения, как прежде, а полное представление о движении камня.

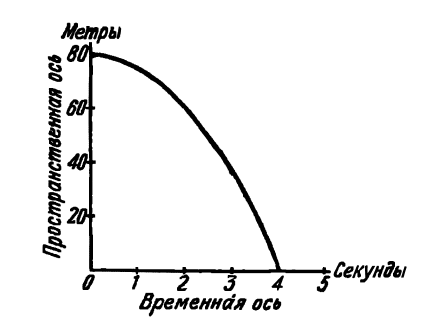
Рис. 63.

Движение вдоль твердого стержня (башни), т. е. движение в одномерном пространстве, представлено здесь в виде кривой в двухмерном пространственно-временно́м континууме. Каждой точке в нашем пространственно-временно́м континууме соответствует пара чисел, одно из которых отмечает временну́ю, а другое – пространственную координату. Наоборот: определенная точка в нашем пространственно-временно́м континууме соответствует некоторой паре чисел, характеризующей событие. Две соседние точки представляют собой два события, прошедшие в местах, близких друг от друга, и в моменты времени, непосредственно следующие друг за другом.

Вы могли бы возразить против нашего способа представления следующим образом: мало смысла в представлении единицы времени отрезком, в его механическом соединении с пространством, образующим двухмерный континуум из двух одномерных континуумов. Но тогда вы должны были бы столь же серьезно протестовать против всех графиков, представляющих, например, изменение температуры в Нью-Йорке в течение последнего лета, или против графиков, изображающих изменение стоимости жизни за последние несколько лет, так как в каждом из этих случаев употребляется тот же самый метод. В температурных графиках одномерный температурный континуум соединяется с одномерным временны́м континуумом в двухмерный температурно-временно́й континуум.

Вернемся к частице, падающей с 80-метровой башни. Наша графическая картина движения есть полезное соглашение, так как она позволяет нам характеризовать положение частицы в любой произвольный момент времени. Зная, как движется частица, мы хотели бы изобразить ее движение еще раз. Сделать это можно двумя путями.

Вспомним изображение частиц, изменяющих свое положение со временем в одномерном пространстве. Мы изображаем движение как ряд событий в одномерном пространственном континууме. Мы не смешиваем время и пространство, применяя динамическую картину, в которой положения изменяются со временем.

Но можно изобразить то же самое движение другим путем. Мы можем образовать статическую картину, рассматривая кривую в двухмерном пространственно-временно́м континууме. Теперь движение рассматривается как нечто, что есть, что существует в двухмерном пространственно-временно́м континууме, а не как нечто, изменяющееся в одномерном пространственном континууме.

Обе эти картины совершенно равноценны, и предпочтение одной из них перед другой есть дело лишь соглашения и вкуса.

То, что здесь сказано о двух картинах движения, не имеет отношения к теории относительности. Оба представления могут быть использованы с одинаковым правом, хотя классическая теория скорее предпочитала динамическую картину описания движения, как того, что́ происходит в пространстве, статической картине, описывающей его в пространстве-времени. Но теория относительности изменила этот взгляд. Она явно предпочла статическую картину и нашла в этом представлении движения, как того, что существует в пространстве-времени, более удобную и более объективную картину реальности. Мы должны еще ответить на вопрос, почему эти две картины эквивалентны с точки зрения классической физики и не эквивалентны с точки зрения теории относительности. Ответ будет понятным, если снова рассмотреть две системы координат, движущиеся прямолинейно и равномерно друг относительно друга.

Согласно классической физике наблюдатели в обеих системах, движущихся прямолинейно и равномерно друг относительно друга, найдут для одного и того же события различные пространственные координаты, но одну и ту же временну́ю координату. Таким образом, в нашем примере удар камня о землю характеризуется при нашем выборе системы координат временно́й координатой «4» и пространственной координатой «0». Согласно классической механике наблюдатели, движущиеся прямолинейно и равномерно относительно выбранной системы координат, обнаружат, что камень достигнет земли спустя четыре секунды после начала падения. Но каждый из наблюдателей относит расстояние к своей системе координат, и они будут, вообще говоря, связывать различные пространственные координаты с событием соударения, хотя временна́я координата будет одной и той же для всех других наблюдателей, движущихся прямолинейно и равномерно друг относительно друга. Классическая физика знает только «абсолютное» время, текущее одинаково для всех наблюдателей. Для каждой системы координат двухмерный континуум может быть разбит на два одномерных континуума: время и пространство. Благодаря «абсолютному» характеру времени переход от «статики» к «динамической» картине движения имеет в классической физике объективный смысл.

Но мы уже убедились в том, что классические преобразования не могут применяться в физике в общем случае. С практической точки зрения они еще пригодны для малых скоростей, но не годятся для обоснования фундаментальных физических вопросов.

Согласно теории относительности момент соударения камня с землей не будет одним и тем же для всех наблюдателей. И временна́я координата, и пространственная координата будут различными в двух различных системах координат, и изменение временно́й координаты будет весьма заметным, если относительная скорость систем приближается к скорости света. Двухмерный континуум не может быть разбит на два одномерных континуума, как в классической физике. Мы не можем рассматривать пространство и время раздельно при определении пространственно-временны́х координат в другой системе координат. Разделение двухмерного континуума на два одномерных оказывается, с точки зрения теории относительности, произвольным процессом, не имеющим объективного смысла.

Все, что мы только что сказали, нетрудно обобщить для случая движения, не ограниченного прямой линией. В самом деле, для описания событий в природе нужно применить не два, а четыре числа. Физическое пространство, постигаемое через объекты и их движения, имеет три измерения, и положения объектов характеризуются тремя числами. Момент события есть четвертое число. Каждому событию соответствуют четыре определенных числа; каким-либо четырем числам соответствует определенное событие. Поэтому: мир событий образует четырехмерный континуум. В этом нет ничего мистического, и последнее предложение одинаково справедливо и для классической физики, и для теории относительности. И опять различие обнаруживается лишь тогда, когда рассматриваются две системы координат, движущиеся друг относительно друга. Пусть движется комната, а наблюдатели внутри и вне ее определяют пространственно-временны́е координаты одних и тех же событий. Сторонник классической физики разобьет четырехмерный континуум на трехмерное пространство и одномерный временно́й континуум. Старый физик заботится только о преобразовании пространства, так как время для него абсолютно. Он находит разбиение четырехмерного мирового континуума на пространство и время естественным и удобным. Но с точки зрения теории относительности время, так же как и пространство, изменяется при переходе от одной системы координат к другой, и преобразования Лоренца рассматривают трансформационные свойства четырехмерного пространственно-временно́го континуума – нашего четырехмерного мира событий.

Мир событий может быть описан динамически с помощью картины, изменяющейся во времени и набросанной на фоне трехмерного пространства. Но он может быть также описан посредством статической картины, набросанной на фоне четырехмерного пространственно-временно́го континуума. С точки зрения классической физики обе картины, динамическая и статическая, – равноценны. Но с точки зрения теории относительности статическая картина более удобна и более объективна.

Даже в теории относительности мы можем еще употреблять динамическую картину, если мы ее предпочитаем. Но мы должны помнить, что это деление на время и пространство не имеет объективного смысла, так как время больше не является «абсолютным». Дальше мы еще будем пользоваться «динамическим», а не «статическим» языком, но при этом всегда будем учитывать его ограниченность.