Трудности, связанные с рациональностью и общеизвестностью рациональности

Тем не менее ноль не оказался выигрышным числом в этом эксперименте в Financial Times. Средним арифметическим было число 19, поэтому победило число 13.

В этом случае принципы рациональности и общеизвестности рациональности не были соблюдены. К примеру, многие участники нерационально выбрали число 100. Даже если бы кто-то ошибочно полагал, что все выберут 100, то оптимальным ответом было бы 67. Такие участники либо не совсем поняли правила игры, либо не смогли посчитать, сколько будет ⅔ от 100.

Концепция рациональности требует от игрока неограниченных когнитивных возможностей. Полностью рациональный человек знает, как решить любую математическую задачу, и может немедленно провести все вычисления, вне зависимости от уровня их сложности. Человеческое поведение можно было бы лучше соотнести с «ограниченной» рациональностью. Это значит, что человеческая рациональность ограничена разрешимостью задачи (то, насколько легко ее можно решить), нашими умственными возможностями, количеством отведенного времени и тем, насколько для нас важно решение этой задачи.

В дополнение к концепции «ограниченной» рациональности, которая имеет большое количество участников, как, например, было в «Игре на угадывание», трудно представить ситуацию, в которой сработал бы принцип общеизвестности рациональности. Даже если все игроки рациональны, вы не выберете 0, если думаете, что остальные игроки не знают, что вы рациональны. Вы бы выбрали число большее, чем 0.

Подъем и крах: применение рациональности на финансовых рынках

«Игра на угадывание» и «Кейнсианский конкурс красоты» объясняют тот интересный факт, что на финансовых рынках даже при условии рациональности всех участников наблюдаются так называемые экономические пузыри – чрезмерно «раздутые» цены. Это связывают с недостатком общеизвестной рациональности.

Игры с одновременными ходами

Часто так случается, что в момент принятия собственного решения игрок не знает, какое действие предпримет соперник. Подобные игры называются играми с одновременными ходами. Иногда игроки принимают решения буквально синхронно, а бывает, проходит какое-то время, но покуда соперники в момент принятия их собственного решения не знают, какой ход выбран другим игроком, мы можем называть их одновременными.

Рассмотрим пример. Кинокомпания Rabbit films сняла захватывающий рождественский фильм о супергероях. Эта лента может быть выпущена в прокат либо в октябре, либо в декабре.

Один из крупнейших конкурентов Rabbit films, кинокомпания Weasel studios, сняла ужасный фильм с огромным бюджетом. По сюжету главные герои этого фильма влюблены друг в друга, но плохая игра актеров не скрывает их взаимной неприязни. Weasel studios также может выпустить фильм в прокат в октябре или в декабре.

Люди чаще ходят в кино в декабре, чем в октябре, поэтому для обеих студий желателен выпуск фильма в декабре. Но оба фильма нацелены на одну аудиторию. Если они появятся в прокате в одно и то же время, то компаниям всеми правдами и неправдами придется бороться за зрителей.

Доход каждой студии зависит не только от даты выхода своего фильма в прокат, но и от даты выхода фильма студии-конкурента. Соответственно, между компаниями наблюдается стратегическое взаимодействие. Выигрыш, который одна студия получит благодаря выбору даты релиза, будет зависеть от выбора соперника.

Стратегическая форма игры

Мы можем проанализировать эту игру, записав возможные действия игроков (релиз фильма в октябре или декабре) и выигрыши (доходы) в таблицу под названием стратегическая (нормальная) форма игры. Стратегическая форма игры – это таблица, известная также как платежная матрица.

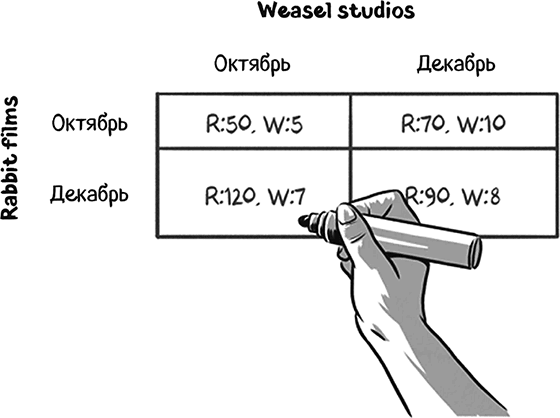
В каждом из двух рядов записан один возможный выбор Rabbit films (октябрь или декабрь), а в каждой колонке записаны возможные выборы Weasel studios. На пересечении каждого ряда и колонки указаны выигрыши каждого игрока: в этом примере под выигрышами понимаются доходы студии.

Эта матрица представляет все возможные исходы игры и указывает, что каждый участник получил бы в качестве выигрыша в каждой конкретной ситуации. Обе киностудии понимают, как работает платежная матрица, и знают, что имеют дело с одной и той же матрицей.

Выигрыши

В каждой конкретной ситуации под выигрышем будет пониматься что-то свое в зависимости от исследуемой проблемы. В примере с релизами фильмов выигрышем являются те многомиллионные доходы, которые с помощью этих фильмов заработали бы студии при любом из возможных исходов.

В иных случаях выигрыши будут иметь другие значения. В биологии выигрышами часто называют приспособленность животного. В экономике, социологии и других науках выигрыш понимается как относительное «благосостояние» или «полезность» участников.

Может показаться странным, что мы связываем с числовыми показателями понятия благосостояния и приспособленности животного. Однако на решения игроков влияют не столько сами числа, сколько то, как эти числа соотносятся.

Для стратегического взаимодействия двух студий важны лишь их предпочтения относительно исхода. Нам важно знать лишь то, какие результаты лучше, а какие хуже для каждого из участников. Числа – это просто удобный способ представления этих предпочтений.

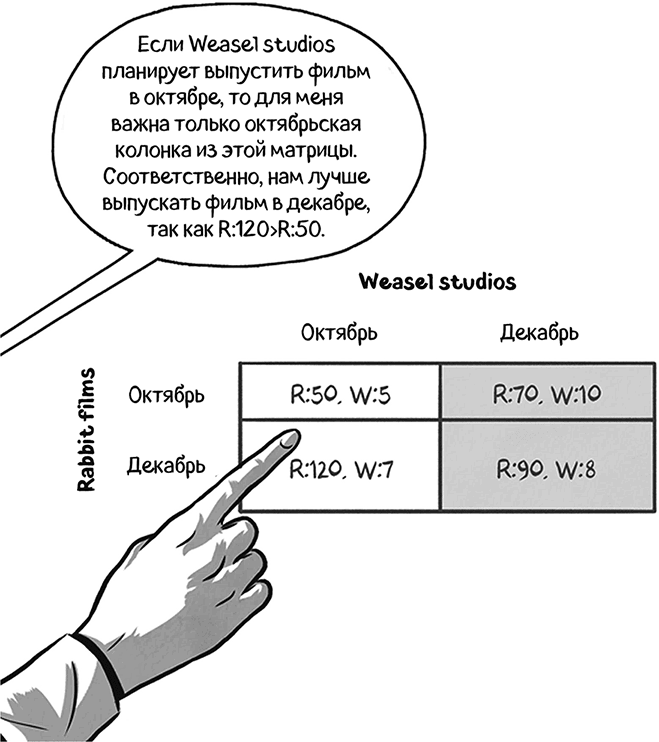
Конечно, существует множество значимых ситуаций, в которых людям важны не только свои собственные выигрыши, но и чужие. Друзья и члены семьи, как правило, стараются радовать друг друга, а пары в состоянии развода и деловые конкуренты могут быть не против причинить друг другу неприятности.

Подобные ситуации легко поддаются анализу с помощью теории игр: записывая потенциальные выигрыши, мы учитываем все желания участников, включая и желания, связанные с личной выгодой, и желание помочь или навредить другим. Значащиеся в таблице числа – это итоговый выигрыш, который каждый из игроков получит при любом из исходов: так, выгода, которую участник способен извлечь, может быть прямой или непрямой (например, если он причинит вред или поможет кому-либо). Таким образом, выигрыш учитывает все, что для человека важно.

Соответственно, в игре стратегической формы каждый игрок заинтересован лишь в увеличении своих выигрышей.