Алан Тьюринг и расцвет компьютерных вычислений
Идеи Алана Тьюринга перевернули весь мир. Он заложил прочную основу для революционного развития современных компьютеров и информационных технологий, а также сделал дальновидные прогнозы по искусственному интеллекту, мозгу и даже биологии развития. Тьюринг также возглавлял разработку решений важных криптоаналитических задач для союзников во время Второй мировой войны.
Чтобы оценить всю важность достижений Тьюринга, стоит узнать, как ученый смог решить одну из самых сложных математических головоломок своего времени и параллельно заложить фундамент для появления всех компьютеров. Истоки ИИ неразрывно связаны с расцветом вычислительной техники.
Первый компьютер
До Второй мировой войны слово «компьютер» обозначало человека (часто – женщину), который выполнял вычисления вручную или с помощью механической счетной машины. Эти человеко-компьютеры были неотъемлемой частью промышленной революции и часто выполняли монотонные вычисления, например для создания книг логарифмических таблиц.
Но в 1936 году Тьюринг, которому на тот момент было всего 24 года, заложил основы для уже знакомого нам типа компьютера и таким образом сыграл ключевую роль в технологической революции. И все же целью Тьюринга не было создание модели современного компьютера. Ученый хотел решить сложную задачу с помощью математической логики. В середине 1930-х годов Тьюринг бесстрашно взялся за решение так называемой Entscheidungsproblem, или «проблемы разрешения», опубликованной математиком Давидом Гильбертом в 1928 году.
К тому времени математики находились в поисках фундаментальных основ, а Гильберт хотел узнать, можно ли считать все математические выражения, вроде 2 + 2 = 4, «разрешимыми». Другими словами, математики пытались понять, существует ли пошаговая процедура, определяющая истинность или ложность любого отдельно взятого математического выражения. Это был фундаментальный вопрос. И хотя мы можем с уверенностью признавать истинность выражения 2 + 2 = 4, интерпретация более сложных логических выражений не так проста. Взять, к примеру, гипотезу Римана, сформулированную Бернхардом Риманом в 1859 году, которая выдавала определенные прогнозы о распределении простых чисел в ряде натуральных. Математики предполагали истинность данной гипотезы, но не могли ее доказать.
Обнаружение предложенной Гильбертом пошаговой процедуры означало бы возможность потенциального создания машины, которая могла бы дать математикам точный ответ на любое логическое выражение. Можно было бы решить все важнейшие математические проблемы. Возможно, тогда это не было столь очевидным, но Гильберт пытался отыскать компьютерную программу. Сегодня его пошаговая процедура называется «алгоритмом». Однако в 1930-х годах не существовало ни компьютеров, ни программ, и Тьюрингу пришлось самостоятельно разработать концепцию вычислений для решения «проблемы разрешения».
В 1936 году Тьюринг опубликовал работу, в которой был представлен четкий ответ на вопрос Гильберта: процедуры для определения истинности или ложности любого математического выражения не существует. Более того, многие из важнейших нерешенных проблем в математике являются неразрешимыми. Это оказалось хорошей новостью для математиков-гуманистов, для которых этот вывод значил, будто бы их никогда не смогут заменить машинами. Но в своей работе Тьюринг представил нечто большее, чем просто решение проблемы Гильберта: в процессе он смог вывести теоретические основы работы современных компьютеров.
Прежде чем тестировать предположение Гильберта, Тьюринг должен был сформулировать эту самую пошаговую процедуру и понять, какое устройство могло бы ее выполнить. Ему не требовалось создавать саму машину – достаточно было понять теоретические принципы ее работы.
Для начала он придумал машину, которая могла считывать символы с перфоленты (см. рис. 1.1). Вы подаете в машину перфоленту, а она изучает символы и на основании заложенных правил принимает решение о своем следующем действии. К примеру, такое устройство могло сложить два числа, записанных на перфоленте, и вывести на ленту результат операции. В дальнейшем это устройство получило название «машина Тьюринга». Но поскольку каждая машина Тьюринга имела собственный свод правил (то есть фиксированную программу), она не годилась для тестирования гипотезы Гильберта.
В 1930-х годах Алан Тьюринг придумал новый тип машин, который смог бы последовательно считывать символы с перфоленты. После принятия решения на основании своих внутренних правил устройство выполняло одно из пяти действий: передвигало ленты вправо или влево, удаляло символ, дописывало новый символ или останавливалось. Такое устройство получило название «машина Тьюринга».
Тьюринг также предположил, что даже саму перфоленту можно использовать для программирования действий машины – то есть базовой версии программного обеспечения. Такая схема получила название «универсальная машина Тьюринга» и стала основой всех современных компьютеров.
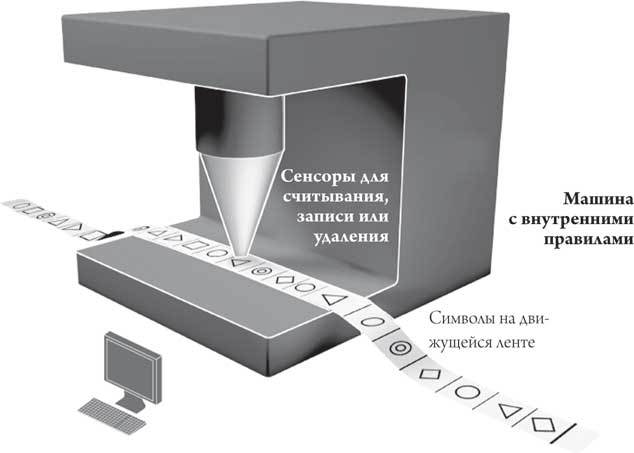
Рис. 1.1. Тьюринг так никогда и не построил свою теоретическую вычислительную машину, но она послужила основой для всех современных компьютеров
Тьюринг понял, что можно создать машину, которая сначала будет считывать процедуру с ленты, а затем использовать эту информацию для определения своих внутренних правил. Таким образом, машина станет программируемой и способной к выполнению тех же действий, что и отдельно взятая машина Тьюринга с фиксированным набором правил. Такое гибкое устройство, которое мы называем «универсальной машиной Тьюринга», и является компьютером.
Почему так? Процедура, записанная на ленте, является аналогом компьютерной программы. Универсальная машина Тьюринга загружает программу с ленты на свое устройство – именно это мы и делаем с программами на жестком диске. Сейчас ваш компьютер используется в качестве текстового процессора, а через минуту он превращается в музыкальный плеер.
Пределы вычислений
После изобретения Тьюрингом теоретического компьютера он смог ответить на вопросы: что такое «вычисляемость»? Что может и не может делать компьютер?
Для опровержения гипотезы Гильберта Тьюрингу нужно было найти лишь одно логическое выражение, которое компьютер не смог бы однозначно трактовать как истинное или ложное. Поэтому Тьюринг сформулировал конкретный вопрос: сможет ли компьютер проанализировать программу и решить, способна ли она «остановиться» или же будет выполняться вечно, до своего отключения? Другими словами, истинен или ложен факт, что программа остановится? Ответ оказался следующим: нет, не сможет. Таким образом, он пришел к выводу, что процедуры Гильберта не существует, и «проблема разрешения» была решена. Фактически вывод Тьюринга заключался в том, что существует бесконечное множество задач, которые компьютер не сможет выполнить.
Пока Тьюринг сражался с проблемой разрешения, американский математик Алонзо Чёрч использовал истинно математический подход к ней. Чёрч и Тьюринг опубликовали свои работы почти одновременно. Работа Тьюринга определяла понятие «вычисляемости», в то время как Чёрч делал упор на «эффективную вычислимость». Оба термина являются равнозначными. Результат их трудов – тезис Чёрча – Тьюринга – лежит в основе нашей концепции пределов вычислений и создает прямую связь между эзотерическим вопросом из математической логики и компьютером на вашем столе или в кармане.
Даже несмотря на существенный прогресс в развитии компьютеров, они до сих пор ограничены пределами, описанными Чёрчем и Тьюрингом. И пускай современные компьютеры в разы мощнее габаритных машин 1940-х годов, они до сих пор способны выполнять только тот же набор задач, что и универсальная машина Тьюринга.
Искусственный мозг
Тьюринг также активно интересовался мозгом. Он был уверен, что мозг ребенка можно смоделировать на компьютере. В 1948 году Тьюринг написал доклад, в котором изложил свою теорию. В процессе написания данной работы он вывел первое описание искусственных нейронных сетей, которые теперь используют для моделирования нейронов.
Его работа оказалась пророческой. К сожалению, доклад не публиковался до 1968 года (через 14 лет после смерти ученого), поскольку директор Национальной физической лаборатории Чарльз Галтон Дарвин охарактеризовал его как «школьное сочинение». Доклад Тьюринга описывал модель мозга, основанную на простых блоках обработки данных – нейронах, которые имеют два входных значения и одно результирующее. Нейроны соединяются в хаотичном порядке и образуют обширную сеть взаимосвязанных блоков. Сигналы, передаваемые по коммутаторам, идентичны синапсам мозга и состоят из единиц и нулей. Сегодня эта модель называется «логической нейронной сетью», но Тьюринг называл ее «неорганизованной машиной типа A».
Машина типа A не могла ничему научиться, поэтому Тьюринг воспользовался ей в качестве основы для обучаемой машины типа B. Машины типа B были идентичны типу A с той лишь разницей, что места соединений между нейронами содержали переключатели, которые можно было «обучить». Обучение сводилось к указанию переключателю включиться (сигнал мог передаваться по синапсу) или выключиться (сигнал блокировался). Тьюринг предположил, что такая схема подойдет для обучения нейронных сетей.
После смерти ученого его идеи были заново открыты, придуманные им простые бинарные нейронные сети отлично подошли для обучения. В частности, они могли научиться распознаванию простых шаблонов (например, формы О и Х). Нельзя не упомянуть о более сложных нейронных сетях. Они заняли центральное место в дальнейших исследованиях ИИ и обусловили успех всех направлений, начиная от беспилотных автомобилей и заканчивая системами распознавания лиц. За всем этим стоял метод, известный как «символическое рассуждение».
Тьюринг: прерванная жизнь
Алан Тьюринг по праву считается одним из величайших умов XX века. Журнал Nature называл его «одним из лучших научных умов всех времен». С такой оценкой сложно не согласиться.
По сути Тьюринг стал отцом информатики. Своей усердной работой и аналитическими знаниями он помог союзникам выиграть Вторую мировую войну. Тьюринг задавал фундаментальные вопросы о природе разума и его связи со структурой мозга. К концу своей жизни ученый взялся за серьезные исследования в области биологии, работая над математической теорией морфогенеза (например, как леопард получает именно такой окрас). Его работы заложили основу новой области биологии, которую признали и начали исследовать только сейчас. Однако столь многогранный, выдающийся и глубокий ум был потерян в 1954 году – Тьюринг покончил с собой после обвинения в «грубой непристойности» за открытую гомосексуальность, которая в то время была запрещена в Великобритании.
Тьюринг умер, когда компьютеры находились в зачаточном состоянии: Фрэнсис Крик и Джеймс Уотсон только открыли структуру ДНК, а искусственный интеллект еще не получил своего названия. Достижения Тьюринга были малоизвестны до 1970-х годов – отчасти из-за гомосексуальности и самоубийства Тьюринга, масштабности математических расчетов в его работах, а также благодаря атмосфере секретности, окружавшей работу ученого в Блетчли-парке.
После декриминализации гомосексуализма в Великобритании в 1967 году и раскрытия секретов Блетчли-парка наследие Тьюринга стало доступным для изучения. Теперь, оглядываясь назад на 41 год жизни Тьюринга и видя его дальнейшее влияние, мы можем лишь представить себе, чего бы смог достичь ученый, проживи он долгую и насыщенную жизнь, которую он заслужил.

