Подтверждение гипотез: программа для решения математических задач

Чистая математика – это еще одно человеческое начинание, подверженное перепадам вдохновения. Программы уже опровергают теоремы, которые люди изо всех сил пытаются доказать. Но смогут ли компьютеры примерить на себя более творческую роль? Если да, то компьютеры будущего переведут математику в области, слишком сложные для нашего восприятия.

В 2012 году Синъити Мотидзуки, уважаемый математик из Киотского университета в Японии, опубликовал на своем сайте более 500 страниц, полностью заполненных вычислениями. Это было кульминацией многолетней работы. Интеруниверсальная теория Тейхмюллера описывала ранее неисследованные математические области и позволяла доказать давний парадокс об истинной природе чисел, известный как АВС-гипотеза. Коллеги-математики оценили результат, но предупредили, что для его проверки потребуются колоссальные усилия. Месяцы работы не приносили плодотворных результатов. Потребовалось целых четыре года, прежде чем кто-то смог разобраться в гипотезе.

Спросите у математика о доказательстве утверждения – скорее всего, вы услышите, что оно должно быть абсолютным, то есть исчерпывающей последовательностью логических шагов, ведущих от установленной отправной точки к неоспоримому выводу. Но это еще не все. Вы не можете просто опубликовать то, во что верите, и спокойно двигаться дальше. Вам нужно убедить других в том, что вы не допустили ни одной ошибки. И действительно революционное доказательство может быть сопряжено с весьма неприятным опытом.

Оказывается, лишь немногие математики готовы отложить в сторону собственную работу и посвятить месяцы или даже годы изучению доказательства Мотидзуки. И поскольку область математики стремительно разделяется на подобласти и подобласти внутри подобластей, проблема становится еще серьезнее. Некоторые ученые полагают, что математика достигла своих пределов.

Реальные открытия могут оказаться слишком сложными для проверки, поэтому многие математики переключаются на более разрешимые и, возможно, менее значимые проблемы. Что же с этим делать?

Для некоторых ученых решение кроется в использовании цифровых помощников. Многие математики уже работают с компьютерами, которые помогают с проверкой доказательств и освобождают время для более творческой работы. Но это может означать изменение и самой математики. Более того, однажды уже сами компьютеры смогут совершить настоящий прорыв в науке. Сможем ли мы идти с ними в ногу? А если нет, то чем это обернется для математики?

Четыре краски

Первое серьезное компьютерное доказательство было опубликовано 40 лет назад и сразу спровоцировало скандал. Это было решение теоремы о четырех красках – головоломки, датируемой серединой XIX века. Теорема утверждает, что во всех картах можно использовать только четыре цвета (краски) для того, чтобы ни одна из смежных областей не была выкрашена в одинаковый цвет.

Можете сами пробовать сколько угодно раз, и вы убедитесь в верности теоремы (см. рис. 5.2). Но для доказательства сначала нужно исключить саму возможность существования фантастической карты, противоречащей теореме.

В 1976 году Кеннет Аппель и Вольфганг Хакен поступили именно так. Они показали, что можно сузить проблему до 1936 наборов карт, для которых может потребоваться пять цветов. Затем каждый из этих потенциальных контрпримеров проверялся компьютером. Ученые обнаружили, что все карты действительно можно раскрасить всего четырьмя цветами.

Вроде бы, работа сделана. Но математики весьма неохотно приняли такие доказательства. А если в код закралась ошибка? Математики не доверяли программам, но никто не хотел вручную перепроверять тысячу примеров. В чем-то они были правы. Проверка программы, тестирующей математическую гипотезу, может оказаться сложнее, чем доказательство той же гипотезы традиционным способом. А ошибка в коде способна сделать все результаты совершенно ненадежными.

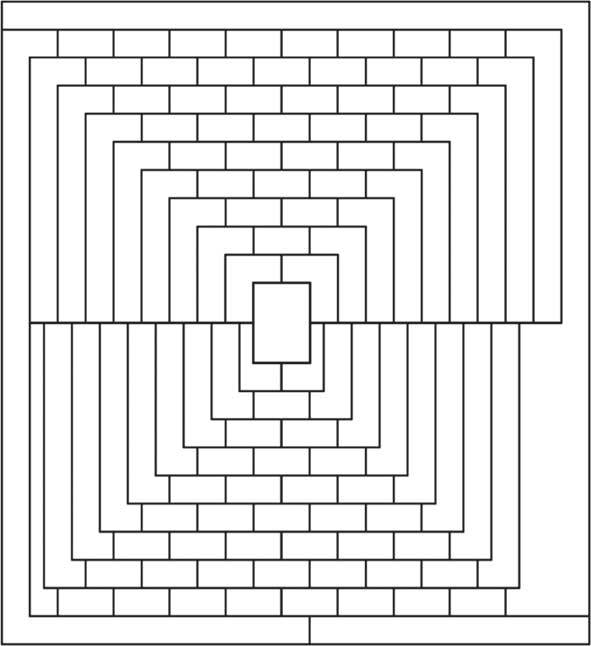
Рис. 5.2. Вы можете раскрасить любую карту с использованием четырех цветов, при этом цвета в смежных областях не будут повторяться. Попробуйте сами на «карте» выше, которая была создана в 1970-х годах писателем и популяризатором математики Мартином Гарднером

Хитрость заключается в том, чтобы проверять одни программы с помощью других. Программные системы доказательства теорем помогут математикам проверить правильность каждого этапа расчетов. Данный процесс является интерактивным. Вы вводите команды в систему, а система их проверяет. Очень похоже на орфокорректор (проверку правописания). А что если в системе проверки возникнет ошибка? Такое всегда возможно, но подобные программы, как правило, достаточно малы и легко проверяются вручную. Более того, многократное выполнение кода показывает вам, что система работает правильно.

Скучные подробности

И все же использование систем доказательства теорем означает изменение принципа работы. Всякий раз, когда математики прописывают доказательства, они опускают множество скучных подробностей. Например, нет смысла каждый раз прикладывать основы расчетов. Но такие сокращения не подойдут для компьютеров, ведь для работы с доказательством они должны учитывать каждый логический и даже самый очевидный шаг, например, почему 2 + 2 = 4.

Перевод «человеческих» доказательств на язык компьютеров все еще остается активной областью исследований. Одно доказательство может занять годы.

Первые достижения проявились в 2005 году, когда команда Жоржа Гонтье из Microsoft Research в Кембридже, Великобритания, обновила доказательство теоремы о четырех красках, сделав каждую ее часть читабельной для компьютера. Все предыдущие версии, начиная с работы Аппеля и Хакена в 1976 году, базировались на математической области под названием «теория графов», которая основывается на нашем пространственном восприятии. Человек может с легкостью расположить области на карте, чего не скажешь о компьютерах. Поэтому исследователям пришлось в корне переработать всю концепцию.

Гонтье обнаружил, что часть доказательства, издавна считавшаяся правильной ввиду своей очевидности, на самом деле не была доказана вообще, поскольку считалось, что это доказательство не стоит затраченных усилий. Оно, конечно, оказалось правильным, но этот случай наглядно продемонстрировал все плюсы дополнительной точности. «Вы должны сводить все решения к алгебре, и для этого требуется большая точность, – говорит он. – Но в результате эта точность гарантированно окупится». Решение теоремы о четырех красках стало лишь началом. «Теорема о четырех красках мало используется в остальных областях математики, – продолжает Гонтье. – Для нас она была просто заковыристой задачей». Поэтому он обратился к теореме Фейта – Томпсона – крупному фундаментальному доказательству в теории групп 1960-х годов. По прошествии многих лет доказательство теоремы было перестроено и переписано, и в конечном итоге его опубликовали в двух книгах. Гонтье надеялся, что формализация теоремы позволит ему продемонстрировать способности компьютера к восприятию более «мясистого» доказательства, которое затрагивало сразу несколько областей математики. Это был идеальный пример.

Непринятые доказательства

Это был успех: в процессе работы исследователи смогли обнаружить несколько мелких ошибок, которые были допущены в книгах. Ошибки быстро исправили. Тем не менее они так и остались визуальным напоминанием того, что не заметил ни один математик-человек. Как сказал Гонтье, многие люди приняли это к сведению. «Я получал письма, в которых люди говорили, что мы написали прекрасную программу». В обоих случаях результат не вызывал сомнений. Гонтье брал общепринятые математические догматы и переводил их на язык компьютеров. Прочим ученым для подтверждения собственных доказательств приходилось самолично переписывать свою работу на понятном для компьютера языке.

В 1998 году Томас Хейлс из Питтсбургского университета, штат Пенсильвания, оказался в том же положении, что и Мотидзуки. Он только что опубликовал 300-страничное доказательство гипотезы Кеплера – 400-летней проблемы о поиске наиболее эффективных способов упаковки набора шаров. Как и в теореме о четырех красках, здесь было возможно несколько тысяч вариантов (способов укладки шаров). Хейлс со своим учеником Сэмюелем Фергюсоном проверил все варианты на компьютере. Он представил полученный ими результат в журнале Annals of Mathematics.

Пять лет спустя рецензенты журнала заявили о том, что на 99 % уверены в правильности доказательства. «Рецензенты-математики, как правило, не стремятся проверять компьютерный код. Они не считают это частью своей работы», – рассказывает Хейлс. Затем в 2003 году убедившийся в своей правоте ученый взялся за переработку доказательства, чтобы затем проверить его с помощью системы автоматического доказательства теорем. По сути он начал заново. Ему потребовалось более десяти лет для завершения проекта. Исследования Гонтье и Хейлса показали, что компьютеры помогают добиться результатов в важнейших областях математики. «Лет десять назад объемные математические теоремы, которые мы сейчас доказываем, казались несбыточной мечтой», – рассказывает Хейлс. Но, несмотря на все новшества в виде системы доказательства теорем, этот процесс остается весьма трудоемким. Большинство математиков не тратят на него время.

Именно поэтому многие ученые стали работать в обратном направлении. Вместо того, чтобы упростить систему доказательства теорем в работе, Владимир Воеводский из Института перспективных исследований в Принстоне, штат Нью-Джерси, предпочитает переделать саму математику в удобную для компьютера форму. С этой целью он взялся за пересмотр всех теоретических основ математики.

Соответствие типу

Это весьма глубокая тема. В настоящее время математика определяется с точки зрения теории множеств, то есть изучает наборы объектов. Например, число ноль определяется как пустое множество, набор без объектов. Единица – это множество, содержащее одно пустое множество. Таким образом можно представить бесконечное количество чисел. Большинство математиков редко волнуются о наборах чисел. Они воспринимают как должное тот факт, что могут понять друг друга, не вдаваясь в лишние подробности.

Но эта схема не подходит для компьютеров, и тут возникает новая проблема. Существует несколько способов определения конкретных математических объектов в терминах множеств. Для нас эти способы не важны, но если два компьютерных доказательства используют разные определения для одного и того же, то такие доказательства окажутся несовместимыми. «Мы не сможем сравнить результаты, поскольку они основаны на разных вещах, – объясняет Воеводский. – Основополагающие принципы математики плохо работают в случаях, если вы хотите уложить все в предельно точную форму».

Альтернативный подход Воеводского заменяет множества типами. Это более строгий способ определения математических объектов, при котором каждому понятию присуще только одно определение. Доказательства, построенные с использованием типов, могут формировать сами типы, что невозможно для множеств.

Данная схема позволяет математикам формулировать идеи в самой системе проверки теорем, а не переводить их на компьютерный язык позже. В 2013 году Воеводский с коллегами опубликовал книгу, которая объясняла принципы, лежащие в основе новой фундаментальной базы. В книге все было представлено наоборот: сначала приводились результаты из системы проверки теорем, а затем данные переводились в понятную для человека форму.

По мнению Гонтье, «обратный способ» работы меняет образ мышления математиков. Он также помогает наладить более тесное сотрудничество между большими группами математиков, ведь им больше не придется постоянно проверять работы друг друга. Результатом станет популяризация идеи о том, что системы доказательства теорем весьма полезны для практических математиков.

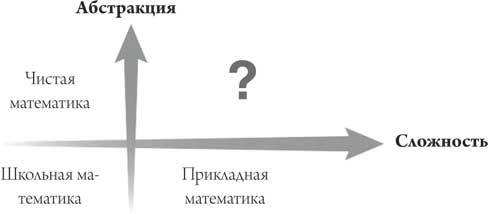
Рис. 5.3. Высоко абстрактная и высоко сложная математика остается за пределами человеческих возможностей. Некоторые ученые считают, что компьютеры смогли бы открыть для нас эту новую область

И все это – только начало. Упрощение математики для компьютеров может открыть для нас совершенно новые области. По мнению Воеводского, работающего над переопределением фундаментальных основ математики, эта наука разделяется на четыре квадранта (см. рис. 5.3). Прикладная математика (например, моделирование воздушного потока над крылом) включает в себя высокую сложность, но низкую абстракцию. Чистая математика (та самая, нарисованная на бумаге и далекая от нашей повседневной жизни) предполагает низкую сложность, но высокую абстракцию. А математика школьного уровня не является ни сложной, ни абстрактной. Но что же находится в четвертом квадранте?

Позабытый

– В наши дни крайне трудно перейти на высокий уровень сложности и абстракции, потому как этот уровень просто не укладывается у нас в головах, – рассказывает Воеводский. – Для высокой сложности и абстракции нужны способности, которых у нас нет.

Вполне возможно, что работа с компьютерами откроет людям доступ к этой четвертой математической области. Мы бы смогли доказывать более крупные, смелые и абстрактные проблемы, возводя наши возможности в математике до небывалых высот.

Может получиться и так, что о нас и вовсе позабудут. В 2014 году Алексей Лисица и Борис Конев из Ливерпульского университета, Великобритания, опубликовали компьютерное доказательство, объем которого составил целых 13 гигабайт, что примерно сопоставимо с размером Википедии. Каждая строка доказательства вполне читаема. Однако для того, чтобы просмотреть все результаты, потребуется прожить несколько длинных человеческих жизней.

С тех пор команда ученых оптимизировала свой код и сократила доказательство до 800 мегабайт. Это значимое улучшение. Однако изучить работу все еще невозможно. Для людей картина выглядит немного иначе. Даже если вы решите посвятить свою жизнь чтению какой-то научной работы, то это будет сравнимо с изучением фотографии по пикселям. В результате вы так и не сможете увидеть всю картину целиком. «Вы не сможете понять идею, стоящую за исследованием», – признается Лисица.

Несмотря на больший масштаб, эта ситуация ничем не отличается от первого доказательства теоремы четырех красок, когда математики все еще сомневались в корректности всестороннего компьютерного поиска. «Мы до сих пор не знаем, почему результат получился верным, – рассказывает Лисица. – Возможно, он ограничен пределами человеческого понимания, поскольку объекты работы действительно огромны». Дорон Цейльбергер из Ратгерского университета в Ньюарке, штат Нью-Джерси, уверен, что настанет время, когда математики-люди не смогут привнести в отрасль ничего полезного. «Все следующее столетие компьютеры будут нуждаться в людях для обучения, – говорит он, – а затем продолжать заниматься этим, но уже в форме интеллектуального спорта. Их машины будут играть друг с другом, как люди играют в шахматы, несмотря на то, что люди во многом уступают машинам».

Цейльбергер – это слишком радикальный пример. Вот уже десять лет он указывает свой компьютер по имени Shalosh B. Ekhad (Шалош Б. Экхад) в качестве соавтора своих работ, а также считает, что людям пора отложить в сторону бумагу и ручку и заняться обучением своих машин. «Самое оптимальное использование времени математика – это передача знаний, – рассказывает он. – Научите компьютеры нужным приемам и позвольте им самим выполнять работу».

Духовная дисциплина

Большинство математиков все же не в восторге от идеи о машинах, способных собирать доказательства за границами человеческого восприятия. «Мысль о том, что когда-то компьютеры заменят математиков, совершенно неуместна», – комментирует Гонтье.

Кроме того, компьютерные математики рискуют утонуть в потоке непрочитанных статей. В настоящее время научные результаты не всегда получают заслуженное признание. Эта проблема особенно актуальна для математики. В 2014 году в онлайн-хранилище arXiv.org каждый месяц выкладывалось свыше 2000 работ по математике – больше, чем по любой другой дисциплине. И этот показатель растет. Многие работы так и остаются незамеченными, поскольку тонут в потоке новых трудов. Одним из способов решения данной проблемы станет создание программы, которая будет читать все опубликованные материалы и передавать людям важную информацию.

Гонтье уверен, что этого недостаточно. «Математика – это не столько поиск доказательств, сколько поиск концепций», – говорит он. По словам Воеводского, сама природа математики находится под пристальным вниманием. А если люди не могут понять доказательства, то это уже не математика. «В будущем математика может стать скорее духовной дисциплиной, нежели прикладным искусством. Одной из важнейших функций математики является развитие человеческого разума».

Но для Синъити Мотидзуки уже слишком поздно. Его работа настолько передовая, настолько далекая от основной математики, что проверить ее с помощью компьютера будет куда сложнее, чем изобрести основное доказательство теоремы. «Я даже не знаю, получится ли официально подтвердить его достижение», – признается Хейлс. Пока что главными судьями остаются люди – пусть даже и не всегда доверяющие себе.