Когда физику Ричарду Фейнману доводилось слушать научную лекцию по теме, в которой он не слишком разбирался, он частенько задавал лектору следующий вопрос: “Не могли бы вы привести простой пример того, о чем идет речь?” Если лектор не мог найти простого примера, это давало Фейнману повод насторожиться – и небезосновательно. Действительно ли лектору было о чем рассказать – или же он просто прикрывался сложными словами, выдавая их за научную мудрость? Если вы не можете сделать сложную задачу относительно простой, вероятно, вы неправильно к ней подходите. Упрощение полезно не только новичкам.

В биологии есть “модельные организмы” – виды, которые были тщательно отобраны, чтобы облегчить труд экспериментаторов: они быстро размножаются в лабораторных условиях, не представляют серьезной опасности и не требуют особенного ухода, а также – после изучения многими научными группами – хорошо описаны и поняты. К этим видам относятся плодовая мушка, лабораторная крыса, полосатый данио, кальмар (имеющий гигантские нервные аксоны), нематода Caenorhabditis elegans и резуховидка Таля (Arabidopsis thaliana) – морозоустойчивое, быстрорастущее цветковое растение, родственное горчице, первое растение, геном которого был полностью секвенирован. В сфере искусственного интеллекта (ИИ) есть свои простые случаи, называемые “модельными задачами”: по сути, они представляют собой предельно упрощенные вариации “серьезных” задач реального мира. Многие из наиболее интересных программ, разработанных на ИИ, представляют собой решения модельных задач – например, как заставить компьютерную программу строить простые объекты в мире кубиков, особом виртуальном мире, где на столе лежат передвигаемые детские кубики. Игра в шахматы – тоже модельная задача, и решить ее, определенно, гораздо проще, чем приехать на машине из Мэна в Калифорнию, положить конец арабо-израильскому конфликту или даже сделать бутерброд из подходящих ингредиентов, найденных на кухне. У этиков есть свои “проблемы вагонетки”: в простейшем варианте неуправляемая вагонетка несется по рельсам и убьет пять человек, которые стоят у нее на пути, если только ее не развернуть, но вы можете перевести стрелку таким образом, чтобы вагонетка ушла на запасной путь и убила бы только одного человека. Переведете ли вы стрелку?

Вот модельный мир, помогающий людям думать о детерминизме, который гласит, что факты – местоположение, масса, направление и скорость каждой частицы, – наблюдаемые в один момент времени, определяют, что случится в следующий момент, и так далее до бесконечности. Физики, философы и другие ученые несколько тысяч лет спорят, является ли наша вселенная детерминистической или же некоторые события на самом деле не предопределены, то есть представляют собой непредсказуемые “случайные” события, которые просто происходят, хотя ничто не заставляет их произойти. Возможно, даже опытные мыслители откроют для себя что-то новое, поиграв с “Жизнью” – поразительно простой моделью детерминистического мира, созданной математиком Джоном Хортоном Конвеем и его студентами в 1970 г.

Игра “Жизнь” ведется на двумерном, размеченном на клетки поле, например на шахматной доске, с использованием простых фишек, например камешков или монеток. Можно также обратиться к высоким технологиям и играть в “Жизнь” на компьютерном экране. Цель игры состоит не в победе; если эту модель вообще можно назвать игрой, то она будет ближе всего к пасьянсу. Каждая из квадратных клеток поля в конкретный момент времени может быть либо “живой”, либо “мертвой”. (Если она “живая”, положите в нее монетку; если “мертвая”, оставьте клетку пустой.) Обратите внимание, что у каждой клетки есть восемь соседей: четыре смежные клетки – север, юг, восток и запад – и четыре диагонали – северо-восток, юго-восток, юго-запад и северо-запад.

Рисунок 1

Время в мире “Жизни” дискретно, а не непрерывно – оно идет шагами, и между этими шагами конфигурация мира меняется по следующему правилу:

Это единственное правило игры. Теперь вы знаете, как играть в “Жизнь”. Вся физика мира “Жизни” описывается этим единственным правилом, из которого нет исключений. Хотя этот фундаментальный закон относится к “физике” мира “Жизни”, на первых порах эту любопытную физику удобно представлять в биологических терминах: считайте, что клетка становится “живой”, когда в ней зарождается жизнь, и “мертвой”, когда эта жизнь угасает, а каждый шаг времени представляет собой смену поколений. Перенаселение (более трех “живых” соседей) и изоляция (менее двух “живых” соседей) приводят к гибели. Рассмотрим несколько простых примеров.

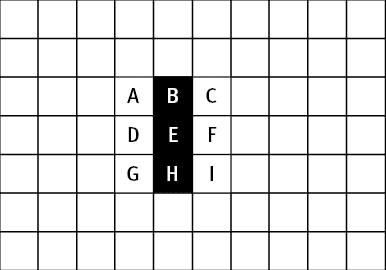
Рисунок 2

В конфигурации, изображенной на рисунке 2, ровно по три “живых” соседа есть только у клеток D и F, поэтому только с них зародится жизнь в следующем поколении. У клеток B и H по одному “живому” соседу, поэтому в следующем поколении они погибнут. У клетки E два “живых” соседа, поэтому она останется “живой”. Таким образом, в следующий “момент” конфигурация будет такой, как на рисунке 3.

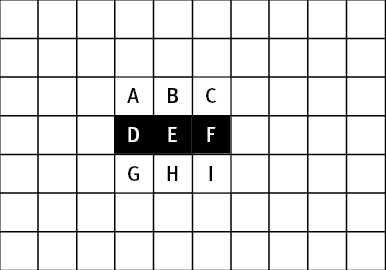
Рисунок 3

Очевидно, в следующий момент восстановится изначальная конфигурация, и это будет повторяться бесконечно, если только в игру каким-то образом не вступят новые “живые” клетки. Такая конфигурация называется мигалкой или светофором. Что произойдет с конфигурацией, изображенной на рисунке 4?

Рисунок 4

Ничего. У каждой “живой” клетки три “живых” соседа, поэтому она перерождается такой же, как была. Ни у одной “мертвой” клетки нет трех “живых” соседей, поэтому нигде не зарождается жизнь. Эта конфигурация называется натюрмортом. Скрупулезно применяя единственный закон “Жизни”, любой может абсолютно точно предсказать, какой станет любая конфигурация “живых” и “мертвых” клеток в следующее мгновение – и в следующее за ним, и так далее. Иными словами, мир “Жизни” представляет собой модельный мир, который прекрасно иллюстрирует детерминизм, прославленный в начале девятнадцатого века французским ученым Пьером Лапласом: имея описание состояния этого мира в некоторый момент времени, мы, наблюдатели, можем в точности предсказать его состояние во все будущие моменты времени, применяя единственный закон физики. Можно сказать иначе: принимая физическую установку в отношении конфигурации в мире “Жизни”, мы получаем совершенные способности к предсказанию – в этом мире нет ни шума, ни неопределенности, ни вероятностей ниже единицы. Более того, двухмерность мира “Жизни” предполагает, что ничто не скрыто из виду. Нет ни закулисья, ни скрытых переменных – физика объектов в мире “Жизни” видна как на ладони.

Если вам скучно следовать простому правилу, можно прибегнуть к компьютерной модели “Жизни”, где вы генерируете изначальную конфигурацию на экране, после чего компьютер выполняет алгоритм за вас, снова и снова изменяя конфигурацию в соответствии с единственным правилом. В лучших моделях можно менять скорость течения времени и масштаб, то приближая конфигурацию, то наблюдая за ней с высоты птичьего полета.

Довольно быстро становится очевидно, что одни простые конфигурации интереснее других. Рассмотрим диагональный отрезок из клеток, изображенный на рисунке 5.

Рисунок 5

Эта конфигурация не мигалка: в каждом поколении две “живых” клетки на концах отрезка умирают в изоляции, а новая жизнь не зарождается. Вскоре весь отрезок исчезает. Помимо неизменных конфигураций – натюрмортов – и конфигураций, которые полностью исчезают, подобно диагональному отрезку, существуют конфигурации различной периодичности. Период мигалки, как мы видели, составляет два поколения, которые будут повторяться до бесконечности, если только не произойдет вторжения другой конфигурации. Вторжения и делают “Жизнь” интересной: среди периодических конфигураций есть такие, которые плывут по полю, подобно амебе. Простейшая из них – планер, пятиклеточная конфигурация, пошагово продвигающаяся на юго-восток на рисунке 6.

Рисунок 6

Существуют также пожиратели, паровозы и космические корабли, а также множество других метко названных обитателей мира “Жизни”, которые становятся узнаваемыми объектами на новом уровне (аналогичном конструктивному уровню). На этом уровне используется свой язык, на котором кратко формулируются точные описания, чересчур затянутые на физическом уровне. Например:

Рисунок 7

Обратите внимание, какая любопытная вещь происходит с нашей “онтологией” – нашим каталогом сущего, – по мере того как мы переходим с уровня на уровень. На физическом уровне нет движения, только “живое” и “мертвое” состояние, а единственные существующие объекты, клетки, определяются фиксированным положением в пространстве. На конструктивном уровне неожиданно появляется движение устойчивых конфигураций: на рисунке 6 на юго-восток движется один и тот же планер (хотя в каждом поколении он состоит из разных клеток), в процессе меняющий форму, а на рисунке 7 в мире становится одним планером меньше, поскольку его поглощает пожиратель.

Также обратите внимание, что на физическом уровне нет никаких исключений из общего правила, а на конструктивном уровне наши обобщения требуют оговорок вроде “обычно” или “если не произойдет вторжения”. Осколки прошлых конфигураций могут “сломать” или “убить” один из объектов онтологии этого уровня. Их салиентность в качестве реальных объектов высока, но не гарантирована. Высокая салиентность предполагает, что можно без особенного риска подняться на этот уровень, принять его онтологию и предсказать – в общих чертах, с оглядкой на риски – поведение крупных конфигураций и систем конфигураций, не просчитывая при этом происходящее на физическом уровне. Например, можно поставить перед собой задачу создать интересную сверхсистему из доступных на конструктивном уровне “элементов”.

Именно этим занялись Конвей и его студенты, которые добились невероятных успехов. Они сконструировали и доказали жизнеспособность самовоспроизводящейся сущности, состоящей целиком из клеток “Жизни”. Работая в соответствии с принципом детерминизма на бесконечном поле, она идеально копировала саму себя, после чего эта копия копировала себя и так далее. Она также (вдобавок) представляла собой универсальную машину Тьюринга – двумерный компьютер, который теоретически может вычислить любую вычислимую функцию! Что же вдохновило Конвея и его студентов создать сначала этот мир, а затем и такого удивительного его обитателя? Они пытались на очень абстрактном уровне ответить на один из главных вопросов биологии: какова минимальная сложность самовоспроизводящегося организма? Они развивали блестящие ранние рассуждения Джона фон Неймана, который работал над этим вопросом до самой своей смерти в 1957 г. Фрэнсис Крик и Джеймс Уотсон открыли ДНК в 1953 г., однако принцип ее работы многие годы оставался тайной. Фон Нейман довольно подробно описал плавающего робота, который подбирал в воде обломки, чтобы сконструировать свою копию, способную впоследствии повторить тот же самый процесс. Его описание того (опубликованное посмертно, в 1966 г.), как автоматон читает собственную схему и копирует ее при создании нового робота, во многом предвосхитило целый ряд позднейших открытий о механизмах экспрессии и репликации ДНК, но чтобы сделать свое доказательство возможности существования самовоспроизводящегося автоманота математически точным и понятным, фон Нейман переключился на простые, двумерные абстракции, которые теперь называют клеточными автоматами. “Жизнь” Конвея представляет собой особенно покладистый клеточный автомат.

Конвей и его студенты хотели подтвердить доказательство фон Неймана, создав двумерный мир с простой физикой, где подобная самовоспроизводящаяся конструкция оказалась бы стабильной, работающей конфигурацией. Как и фон Нейман, они хотели получить как можно более общий ответ, который был бы максимально независим от фактической (земной? местной?) физики и химии. Им хотелось, чтобы модель получилась предельно простой для расчетов и визуализации, поэтому они не только перешли от трехмерного мира к двумерному, но и “оцифровали” пространство и время: как мы видели, время и расстояние в “Жизни” всегда выражается целыми числами “мгновений” и “клеток”. Именно фон Нейман взял абстрактную концепцию механического компьютера Алана Тьюринга (теперь ее называют машиной Тьюринга) и сделал из нее универсальный серийный компьютер с хранимой в памяти программой (теперь его называют машиной фон Неймана), а также в ходе блестящих исследований пространственных и структурных требований для создания такого компьютера обнаружил – и доказал, – что универсальную машину Тьюринга (см. раздел IV) теоретически можно “сконструировать” в двумерном мире. Конвей и его студенты также решили подтвердить это, поупражнявшись в двумерной инженерии.

Им пришлось нелегко, но они показали, как “сконструировать” рабочий компьютер из простых форм “Жизни”. Потоки планеров могут, к примеру, служить “лентой” ввода и вывода, а в качестве управляющего устройства может использоваться крупная конфигурация пожирателей, планеров и других элементов. Как выглядит эта машина? Паундстоун (1985) вычислил, что вся конструкция займет около 10¹³ клеток, или пикселей.

Иными словами, когда достаточное количество элементов составит способную к самовоспроизводству конфигурацию (в двумерном мире), эта конфигурация будет примерно во столько же раз больше каждого из элементов, во сколько организм больше атома. Вероятно, создать способную к самовоспроизводству систему значительно меньшей сложности невозможно, однако это пока не доказано.

Игра “Жизнь” иллюстрирует многие важные принципы и может быть использована для построения множества аргументов и мысленных экспериментов, однако я с ее помощью подчеркну лишь три момента, чтобы остальное вы открыли сами. Во-первых, обратите внимание, как в ней размывается различие между физической и конструктивной установкой. Считаются ли планеры, к примеру, сконструированными или природными объектами (подобно атомам и молекулам)? Если на то пошло, управляющее устройство, составленное Конвеем и его студентами из планеров, пожирателей и тому подобных элементов, уж точно должно считаться сконструированным, но его элементы представляют собой сырье – простейшие “объекты” мира “Жизни”. Никому не пришлось конструировать или изобретать планер – он был открыт как подразумеваемый физикой мира “Жизни” объект. Впрочем, это относится к любому объекту мира “Жизни”. В этом мире не происходит ничего, что не подразумевалось бы – то есть не было бы логически выводимо посредством доказательства теорем – физикой и изначальной конфигурацией клеток. Одни объекты мира “Жизни” просто более удивительны и неожиданны (для нас, с нашим жалким интеллектом), чем другие. В определенном смысле самовоспроизводящаяся компьютерная пиксельная галактика Конвея – “лишь” еще одна макромолекула “Жизни”, для которой характерна особенно долгая и сложная периодичность. Таким образом иллюстрируется параллельный тезис о биологии и происхождении жизни: можно сказать, что аминокислоты просто есть – их не нужно было конструировать. Но белки, состоящие исключительно из аминокислот, слишком сложны – они, по крайней мере, вроде как сконструированы. И снова мы сталкиваемся с градуализмом Дарвина.

Во-вторых, мир “Жизни”, будучи детерминистическим, располагает в полной мере предсказуемым будущим для любой возможной конфигурации, но, как ни странно, его прошлое часто бывает совершенно непостижимо! Рассмотрим натюрморт из четырех “живых” пикселей в квадрате. При взгляде на него – и даже при взгляде на него и его соседей – невозможно сказать, каким было его прошлое. Чтобы заметить это, обратите внимание, что любые три из четырех “живых” пикселей в следующем поколении приведут к формированию натюрморта из этих четырех “живых” пикселей. Была ли хоть одна из этих клеток в прошлом “мертвой” – инертный исторический факт.

В-третьих, вспомните, как важен “шум” и столкновения для создания мутаций, которыми питается эволюция – и другие творческие процессы. Гигантская конфигурация Конвея воспроизводила себя, но не могла мутировать. Она всегда создавала бы свою совершенную копию, а чтобы включить в картину мутации, конфигурацию пришлось бы многократно увеличить. Почему? Потому что в детерминистическом мире “Жизни” “случайная” мутация может произойти, только если появится (псевдослучайным образом) фрагмент, который что-то сломает. Но самым маленьким движущимся объектом остается планер, так что можете представить его в виде отдельного фотона, или космического луча, движущегося со скоростью света (физики мира “Жизни”). Единственный планер может причинить немало вреда – если он должен только “подправить” что-то в геноме самовоспроизводящейся конфигурации, не разрушая генома, этот геном должен быть огромным в сравнении с планером и довольно крепким. Возможно, если бы выяснилось, что гигантские конфигурации размером с галактику слишком хрупки, чтобы пережить редкий дождь из планеров, нашелся бы и способ доказать, что эволюция в мире “Жизни” невозможна, какими бы большими ни были эти конфигурации.