Книга: Насосы интуиции и другие инструменты мышления
Назад: IV. Интерлюдия о компьютерах
Дальше: 25. Виртуальные машины
24. Семь секретов силы компьютеров
Компьютеры наделены силами, которые несколько веков назад показались бы чудесными – “настоящей магией”. При этом, хотя многие компьютерные программы невероятно сложны, все они состоят из шагов, которые в полной мере объясняются очень простыми словами. В работе компьютеров нет места чудесам. Само это отчасти обусловливает ценность компьютеров в качестве инструментов мышления, и потому возможность объяснить – в общих чертах – принцип работы компьютера весьма интересна с философской точки зрения. Никому не помешает на элементарном уровне разобраться, как компьютеры творят свою “магию”. В этой главе фокус будет разоблачен.
Для начала мы представим себе простейший компьютер – регистровую машину – и проанализируем его возможности и принцип работы. Затем мы увидим, что машина Тьюринга и машина фон Неймана (например, ваш ноутбук) ничем не отличаются от регистровых машин, только работают более эффективно. (Все, что под силу вашему ноутбуку, под силу и регистровой машине, но не обольщайтесь – на это у нее могут уйти столетия.) После этого мы разберем, как “архитектуры” других компьютеров могут повысить скорость работы и производительность нашей базовой регистровой машины. Само собой, интереснее и полезнее всего будет изучить архитектуру человеческого мозга.
Погодите-ка. Неужели я только что сказал, что ваш мозг – это просто гигантский компьютер? Нет, пока я такого не сказал. Я говорю, что если ваш мозг представляет собой гигантский компьютер, то найдется способ полностью объяснить его работу, не оставив никаких тайн, но только если мы сумеем обнаружить этот способ. Мы обратимся к обратному проектированию: будем изучать сложную систему, чтобы выяснить, каким образом она функционирует. Обратное проектирование позволяет нам понять, как сердце качает кровь и как легкие поглощают кислород и отдают углекислый газ. Нейробиология делает попытку применить обратное проектирование к мозгу. Мы знаем, зачем нам нужен мозг – чтобы предвидеть, направлять нас, запоминать и усваивать информацию, – но теперь нам нужно понять, каким образом он это делает.
Споры на эту тему не утихают. Писатель Том Вулф (2000) заострил внимание на больном месте, которое провоцирует ожесточенные баталии, озаглавив свое эссе “Мне жаль, но ваша душа скончалась”. Если мы намереваемся вступить на эту опасную территорию – не тратя времени на разглагольствования и разоблачения, – нам нужны инструменты получше. Прежде чем добросовестно взяться за вопрос, таит ли и использует ли наш мозг не поддающиеся пониманию или чудесные феномены, недоступные никаким компьютерам, нам нужно понять, на что способны компьютеры и как именно они функционируют. Единственный удовлетворительный способ продемонстрировать, что наш мозг не тождественен – и не может быть тождественен – компьютеру, заключается в том, чтобы показать либо (1) что ряд его “подвижных частей” участвует в процессах обработки информации, в которых не могут участвовать компьютеры, либо (2) что простые процессы, в которых задействованы его части, не могут быть сконструированы, агрегированы и организованы на компьютерный манер, чтобы сымитировать знакомые и любимые нами умения сознания.
Некоторые эксперты – не только философы, но и нейробиологи, психологи, лингвисты и даже физики – утверждают, что “компьютерная метафора” для описания работы человеческого мозга или сознания категорически неверна, а мозгу – что важнее – под силу такие вещи, на которые не способны компьютеры. Обычно, но не всегда, такая критика предполагает весьма наивное представление о том, что такое компьютер или каким он должен быть, и в итоге лишь доказывает очевидную (и не относящуюся к делу) истину, что мозг умеет делать множество вещей, которых не умеет ваш ноутбук (учитывая ограниченное количество его преобразователей и эффекторов, ничтожный объем памяти и низкую скорость работы). Если оценивать эти громкие скептические заявления о возможностях компьютеров в принципе, нужно понимать, откуда в принципе берется вычислительная мощность, как она используется и как может использоваться.
Блестящую идею создания регистровой машины на заре компьютерной эры предложил логик Хао Ван (1957), между прочим, студент Курта Гёделя и философ. Это изящный инструмент мышления, который вам стоит иметь в своем наборе. Он далеко не так известен, как должен бы. Регистровая машина – это идеализированный, воображаемый компьютер (который вполне можно сконструировать), состоящий из некоторого (конечного) числа регистров и блока обработки данных.
Регистры – это ячейки памяти, каждая из которых имеет уникальный адрес (регистр 1, регистр 2, регистр 3 и так далее) и может содержать одно целое число (0, 1, 2, 3…). Каждый регистр можно представить в виде большого ящика, содержащего произвольное количество бобов, от 0 до …, вне зависимости от размеров ящика. Обычно мы считаем, что в ящике может содержаться любое целое число, поэтому ящики, само собой, должны быть бесконечно большими. Для наших целей подойдут и просто очень большие ящики.
Блок обработки данных имеет всего три простых компетенции, три “инструкции”, которым он может “следовать” пошагово, выполняя одну зараз. Любая последовательность этих инструкций представляет собой программу, и каждой инструкции присвоен номер, чтобы ее идентифицировать. Инструкции таковы:
Конец работы. Машина может остановиться или выключиться.Инкремент регистра n (прибавить 1 к содержимому регистра n; положить один боб в ящик n) и переход на следующий шаг, шаг m.Декремент регистра n (отнять 1 от содержимого регистра n; вынуть один боб из ящика n) и переход на следующий шаг, шаг m.
Инструкция “декремент” работает точно так же, как инструкция “инкремент”, но между ними есть одно принципиально важное различие: что делать, если в регистре n содержится число 0? Машина не может отнять 1 от этого содержимого (в регистрах не могут содержаться отрицательные числа; боб из пустого ящика не вынуть), поэтому, оказавшись в безвыходном положении, машина должна сделать “переход”. Иными словами, она должна обратиться к другому фрагменту программы, чтобы получить следующую инструкцию. В связи с этим каждая инструкция “декремент” должна определять, к какому фрагменту программы обращаться, если в текущий момент в регистре содержится 0. Таким образом, полное определение инструкции “декремент” звучит так:
Декремент регистра n (отнять 1 от содержимого регистра n), если это возможно, и переход на шаг m ИЛИ, если декрементировать регистр n невозможно, переход на шаг p.
Теперь снабдим все возможности регистровой машины короткими названиями: Кон, Инк и Деп (декремент-или-переход).
На первый взгляд может показаться, что такая простая машина не способна ни на что особенно интересное, ведь она умеет лишь класть боб в ящик или вынимать боб из ящика (если там есть боб – и переходить к другой инструкции, если его нет). Но на самом деле она может производить такие же вычисления, которые умеет производить любой другой компьютер.
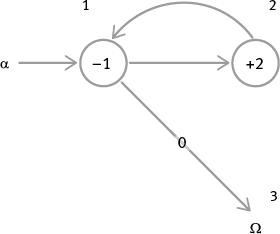
Начнем с простого сложения. Допустим, вы хотите, чтобы регистровая машина прибавила содержимое одного регистра (скажем, регистра 1) к содержимому другого регистра (регистра 2). Таким образом, если в регистре 1 содержится [3], а в регистре 2 содержится [4], мы хотим, чтобы в итоге программа сделала так, чтобы содержимое регистра 2 стало равняться [7], потому что 3 + 4 = 7. Вот программа, которая справится с этой задачей, написанная на простом языке РПА (регистровое программирование на ассемблере):
программа 1: ADD [1,2]

Первые две инструкции образуют простой цикл, в рамках которого регистр 1 декрементируется, а регистр 2 инкрементируется снова и снова, пока регистр 1 не опустеет. Это “заметит” блок обработки данных, который в результате сделает переход на шаг 3, останавливающий программу. Блок обработки данных не может сказать, каково содержимое регистра, если только это содержимое не 0. Если снова представить ящики с бобами, можно сказать, что блок обработки данных слеп и не видит, что находится в регистре, пока он не опустеет, потому что отсутствие содержимого он может определить на ощупь. Несмотря на то что, в принципе, он не может сказать, каково содержимое регистров, если задать ему программу 1, он всегда будет прибавлять содержимое регистра 1 (какое бы число ни содержалось в регистре 1) к содержимому регистра 2 (какое бы число ни содержалось в регистре 2), а затем останавливаться. (Вы понимаете, почему так должно происходить всегда? Разберите несколько примеров, чтобы удостовериться.) Вот любопытный способ на это взглянуть: регистровая машина мастерски умеет складывать числа, не зная, какие именно числа она складывает (а также что такое числа и что такое сложение)!
упражнение 1
а. Сколько шагов потребуется регистровой машине, чтобы сложить 2 + 5 и получить 7, выполняя программу 1 (считая Кон отдельным шагом)?б. Сколько шагов потребуется машине, чтобы сложить 5 + 2?(Какой из этого можно сделать вывод?)
Этот процесс можно изобразить наглядно, построив так называемый граф потока. Каждый кружок обозначает инструкцию. Число в кружке обозначает адрес регистра, с которым необходимо произвести манипуляции (а не содержимое регистра), “+” обозначает инструкцию Инк, а “–” – инструкцию Деп. Программа всегда начинается с α, альфы, и завершается, когда достигает Ω, омеги. Стрелки показывают переход к следующей инструкции. Обратите внимание, что каждая инструкция Деп имеет две исходящих стрелки, одну для направления, в котором двигаться, если декрементировать содержимое регистра возможно, а другую – если невозможно, потому что содержимое регистра 0 (переход на ноль).
Теперь давайте напишем программу, которая просто перемещает содержимое одного регистра в другой регистр:
программа 2: MOVE [4,5]

Вот граф потока:
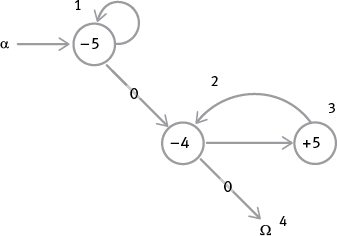
Обратите внимание, что первый цикл этой программы очищает регистр 5, так что, каким бы ни было его содержимое в самом начале, оно никак не повлияет на то, что окажется в регистре 5 ко второму циклу (циклу сложения, в ходе которого содержимое регистра 4 прибавляется к 0 в регистре 5). Этот начальный шаг называется обнулением регистра и представляет собой весьма употребительную стандартную операцию. Вы постоянно будете использовать ее, чтобы готовить регистры к использованию.
Третья простая программа копирует содержимое одного регистра в другой регистр, оставляя изначальное содержимое нетронутым. Изучите граф потока, а затем саму программу:
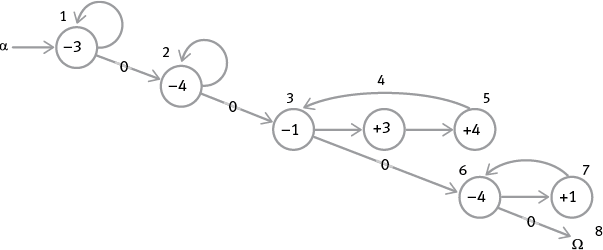
программа 3: COPY [1,3]
Это явно не самый очевидный способ копирования, поскольку мы осуществляем операцию, сначала перемещая содержимое регистра 1 в регистр 3, затем делая копию в регистре 4 и, наконец, перемещая эту копию обратно в регистр 1. Но это работает. Всегда. Каким бы ни было содержимое регистров 1, 3 и 4 в самом начале, когда программа остановится, содержимое регистра 1 останется на месте, а копия этого содержимого – в регистре 3.
Если принцип работы этой программы вам не очевиден, возьмите несколько чашек, чтобы сделать регистры (подпишите номер каждой чашки, ее адрес), и горстку монеток (или бобов) и “вручную смоделируйте” весь процесс. Положите по несколько монеток в каждый из регистров и обратите внимание, сколько именно монеток вы положили в регистр 1 и регистр 3. Если вы будете в точности следовать программе, когда вы закончите, количество монеток в регистре 1 будет таким же, каким оно было изначально, и такое же количество монеток будет лежать в регистре 3. Очень важно, чтобы вы усвоили базовый принцип работы регистровой машины и вам не пришлось больше ломать над ним голову, поскольку мы собираемся использовать этот новый навык в дальнейшем. Выделите несколько минут и станьте регистровой машиной (как актер может стать Гамлетом).
Я замечаю, что некоторые мои студенты совершают простую ошибку: им кажется, что при декрементировании регистра монетку, которую они только вынули из регистра n, нужно положить в какой-нибудь другой регистр. Нет. Декрементированные монетки просто возвращаются в общую кучу, в ваш “бесконечный” запас монеток для использования в этих простых операциях сложения и вычитания.
Научившись перемещать, копировать и обнулять содержимое регистров, мы можем улучшить нашу программу сложения. Программа 1 помещает верный ответ на задачу на сложение в регистр 2, но в процессе уничтожает изначальное содержимое регистров 1 и 2. Возможно, нам нужна более сложная программа сложения, которая сохраняет эти значения для последующего использования, помещая ответ в другой регистр. Попробуем прибавить содержимое регистра 1 к содержимому регистра 2, поместить ответ в регистр 3 и оставить содержимое регистров 1 и 2 нетронутым.
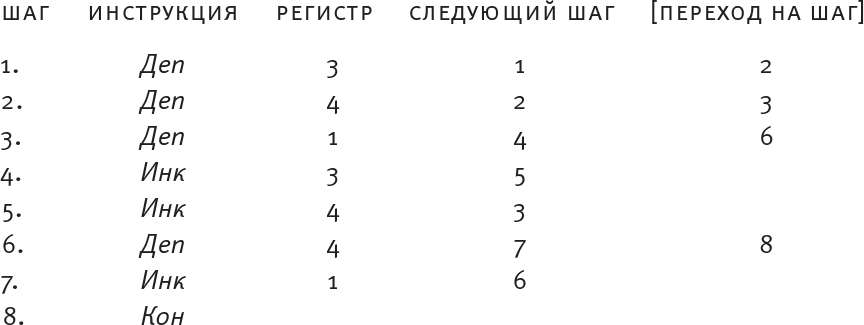
Вот граф потока, показывающий, как этого добиться:
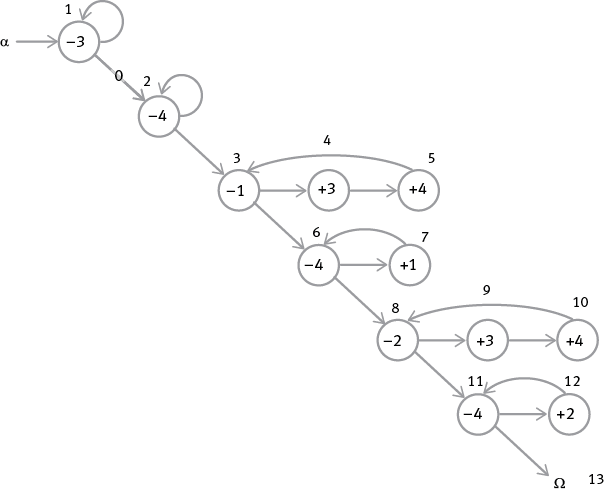
Проанализируем циклы, чтобы понять, что делает каждый из них. Сначала мы обнуляем регистр ответа, регистр 3, а затем обнуляем дополнительный регистр (регистр 4), который станет временным хранилищем, или буфером. После этого мы копируем содержимое регистра 1 в регистры 3 и 4 и перемещаем это содержимое обратно из буфера в регистр 1, восстанавливая его (и в процессе обнуляя регистр 4, чтобы снова использовать его в качестве буфера). Затем мы повторяем эту операцию с регистром 2, фактически прибавляя содержимое регистра 2 к содержимому, которое мы уже переместили в регистр 3. Когда программа останавливается, буфер 4 снова оказывается пуст, ответ находится в регистре 3, а два числа, которые мы складывали, – на своих изначальных местах, в регистрах 1 и 2.
Вот написанная на РПА 13-шаговая программа, которая переводит всю информацию с графа потока на язык, понятный блоку обработки данных:
программа 4: ADD [1,2,3] без разрушения
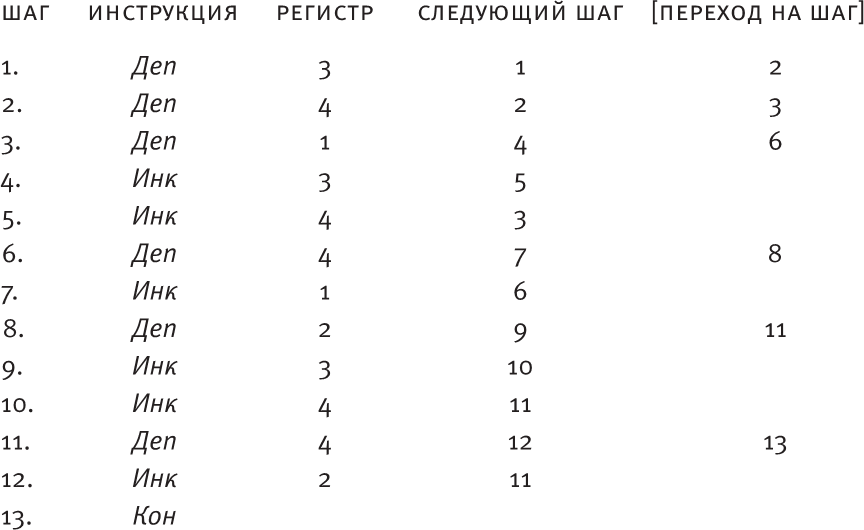
Я не буду советовать вам вручную смоделировать эту программу, используя чашки и монетки. Жизнь коротка, поэтому, когда вы усвоите все базовые процессы, вам можно будет пользоваться вспомогательным устройством RodRego, регистровой машиной, которую можно скачать по ссылке http://sites.tufts.edu/rodrego/.
Есть версии RodRego для Windows и для Mac. Мы разработали этот инструмент мышления более двадцати лет назад в Мастерской учебных программ, и с тех пор сотни студентов и других заинтересованных людей воспользовались им, чтобы поднатореть в программировании регистровых машин. Вводя программы на РПА, вы можете наблюдать за их исполнением, выбирая режим с цифрами или бобами в регистрах. На той же странице представлена анимированная PowerPoint-презентация, в которой показан путь блока обработки данных по графу потока при совершении, к примеру, операции сложения. Эта анимация позволяет увидеть, как инструкции РПА соотносятся с кружками графа потока.

Теперь обратимся к вычитанию. Вот первый фрагмент графа потока для вычитания содержимого регистра 2 из содержимого регистра 1 и помещения ответа в регистр 4. Можете сказать, что с ним не так?
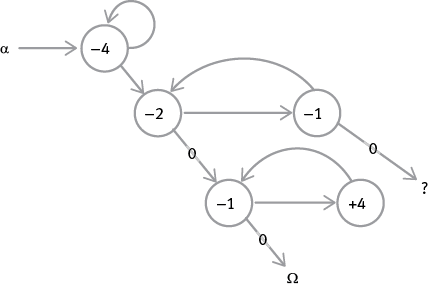
Такая программа сработает, только если содержимое регистра 1 больше содержимого регистра 2. Но что если это не так? Регистр 1 “обнулится” на середине цикла вычитания, когда вычитание еще не будет закончено. И что тогда? Мы не можем просто велеть компьютеру завершить выполнение программы, поскольку ответ в регистре 4 окажется неверным (0). Мы не можем использовать это обнуление, чтобы начать новый процесс, который сначала возвращается на половину цикла и отменяет временное декрементирование регистра 2. На этом этапе содержимое регистра 2 (а не регистра 1) даст нам верный ответ, если мы интерпретируем его в качестве отрицательного числа, так что вы можете просто переместить это содержимое в регистр 4 (который уже обнулен) и где-нибудь обозначить, что число в ответе отрицательное. Логично зарезервировать для этой задачи отдельный регистр – скажем, регистр 3. В самом начале его необходимо обнулить вместе с регистром 4, а затем поставить в регистре 3 “метку”, определяющую, положительное число в ответе или отрицательное, при условии что 0 означает +, а 1 означает –. Ниже представлен граф потока с комментариями, объясняющими, что происходит на каждом шаге цикла. (Вы можете добавлять такие комментарии в свои программы РПА, ограничивая их знаками #. Они предназначены для вас и других людей; RodRego их просто проигнорирует.)
упражнение 2
а. Напишите РПА-программу для этого графа потока. (Обратите внимание: поскольку программа разветвляется, вы можете пронумеровать шаги несколькими способами. Неважно, какой из них вы выберете: главное, чтобы на верные следующие шаги указывали команды безусловного перехода.)
б. Что происходит, когда программа пытается вычесть 3 из 3 или 4 из 4?
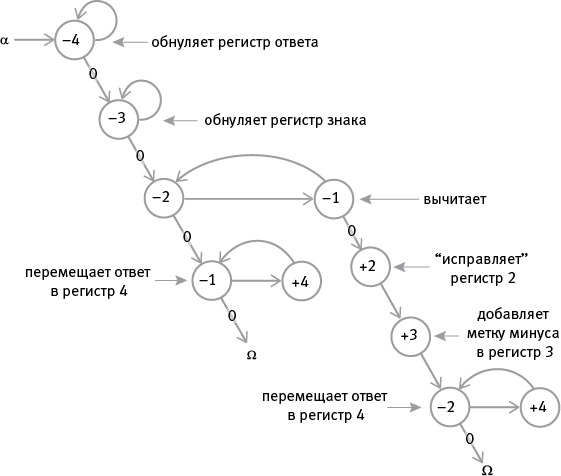
в. Какая возможная ошибка предотвращается обнулением регистра 3 перед попыткой вычитания на шаге 3 вместо шага 4?
Умея складывать и вычитать, мы легко можем разработать программы для умножения и деления. Чтобы умножить n на m, нужно просто прибавить n к самому себе m раз. Мы можем запрограммировать компьютер сделать это, используя один регистр как счетчик, который считает от m до 0, осуществляя одну операцию декрементирования по завершении каждого цикла сложения.
упражнение 3
а. Нарисуйте граф потока (и напишите РПА-программу) для умножения содержимого регистра 1 на содержимое регистра 3, поместив ответ в регистр 5.
б. (По желанию) Используя копирование и перемещение, улучшите программу умножения, созданную в задаче а: когда она закончит работу, изначальное содержимое регистра 1 и регистра 3 восстановится, так что вы сможете легко проверить исходные данные и ответы на правильность по завершении программы.
в. (По желанию) Нарисуйте граф потока и напишите РПА-программу, которая изучает содержимое регистра 1 и регистра 3 (не разрушая их!) и записывает адрес (1 или 3) регистра с большим содержимым в регистр 2 или помещает 2 в регистр 2, если содержимое регистров 1 и 3 равно. (После выполнения этой программы содержимое регистра 1 и регистра 3 должно остаться неизменным, а регистр 2 должен показывать, равно ли их содержимое, а если нет, то в каком из регистров содержимое больше.)
Деление можно выполнять подобным образом, снова и снова вычитая делитель из делимого и считая, сколько раз мы можем провести эту операцию. Остаток – при наличии – можно поместить в специальный регистр для остатка. Но здесь обязательно нужно ввести важную меру предосторожности: на ноль делить нельзя (или можно?), поэтому перед началом деления необходимо провести простую проверку делителя, попробовав его декрементировать. Если его получилось декрементировать, нужно один раз его инкрементировать (чтобы восстановить его исходное значение), а затем провести деление. Если же в регистре ноль, после неудачной попытки декремента нужно поднять тревогу. Можно сделать это, зарезервировав регистр для метки ошибка: 1 в регистре 5 может означать “тревога! Меня только что попросили поделить на ноль!”.
Ниже представлен граф потока для деления содержимого регистра 1 на содержимое регистра 2, помещения ответа в регистр 3 и остатка в регистр 4 и резервирования регистра 5 для “сообщения об ошибке” (1 означает “меня попросили поделить на ноль”).
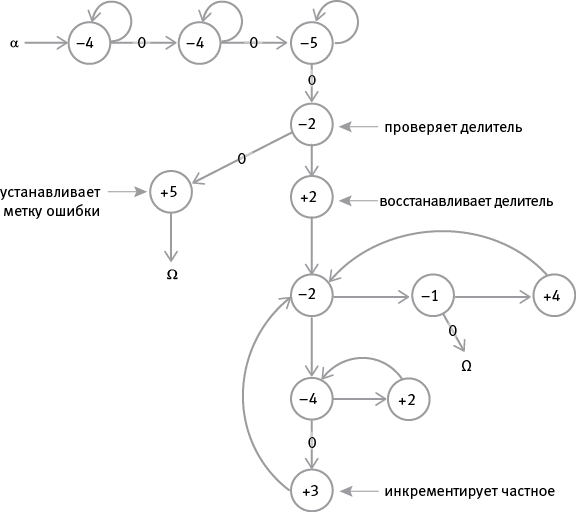
Изучите граф и обратите внимание, что ноль в делителе прерывает операцию и выдает сообщение об ошибке. Кроме того, заметьте, что регистр 4 служит двум целям: он не только выполняет роль копии делителя для восстановления делителя после каждой следующей операции вычитания, но и зарезервирован для потенциального остатка. Если регистр 1 обнуляется, прежде чем регистр 4 получает возможность вернуть свое содержимое обратно в регистр 2 для следующей операции вычитания, это содержимое и становится остатком, оказавшемся на своем месте.
секрет 1. Компетентность без понимания. Нечто – например, регистровая машина – может точно выполнять арифметические действия, не понимая, что делает.
Регистровая машина не тождественна сознанию. Она ничего не понимает, но вроде как понимает три простые вещи – Инк, Деп и Кон – в том смысле, что всякий раз слепо выполняет три этих “инструкции”. Само собой, это не настоящие инструкции, а лишь вроде как инструкции. Они кажутся нам инструкциями, и регистровая машина выполняет их так, как если бы они были инструкциями, так что нам более чем удобно называть их инструкциями.
Как вы теперь видите, эффективность регистровой машины объясняется существованием инструкции Деп, декремент-или-переход. Только эта инструкция позволяет компьютеру “замечать” (вроде как замечать) что-то в мире и использовать свои наблюдения для выбора следующего шага. Фактически существованием этой команды условного перехода объясняется эффективность всех компьютеров с хранимой в памяти программой, на что Ада Лавлейс обратила внимание еще в девятнадцатом веке, когда написала блестящий комментарий к описанию аналитической машины Чарльза Бэббиджа, которая стала прототипом всех компьютеров.
Когда вы наловчитесь собирать программы по частям, это станет для вас обычным делом. Однажды написав арифметические программы, мы можем использовать их снова и снова. Допустим, мы пронумеруем их: ADD станет операцией 0, SUBTRACT – операцией 1, MULTIPLY – операцией 2 и так далее. COPY может стать операцией 5, MOVE – операцией 6 и т. д. Теперь мы сможем использовать регистр, чтобы хранить в нем инструкцию, обозначая ее присвоенным номером.
упражнение 4 (по желанию)
Нарисуйте граф потока и напишите РПА-программу, которая превращает регистровую машину в простой карманный калькулятор, следующим образом:
а. Используйте регистр 2 для операции:
0 = ADD
1 = SUBTRACT
2 = MULTIPLY
3 = DIVIDE
б. Поместите числа, с которыми будут производиться манипуляции, в регистры 1 и 3.
(Таким образом, 3 0 6 будет означать 3 + 6; 5 1 3 будет означать 5–3; 4 2 5 будет означать 4 * 5; а 9 3 3 будет означать 9 ÷ 3.) Затем поместите результаты операции в регистры 4–7, используя регистр 4 для знака (где 0 означает +, а 1 означает –), регистр 5 для численного ответа, регистр 6 для возможного остатка в случае деления, а регистр 7 для сообщения об ошибке ввода (либо требовании делить на ноль, либо неопределенной операции в регистре 2).
Обратите внимание, что в этом примере содержимое регистров (которое всегда представляет собой число) используется для обозначения четырех совершенно разных вещей: числа, арифметической операции, знака числа и метки ошибки.
секрет 2. Что именно обозначает число в регистре, определяет созданная нами программа.
Используя уже созданные структурные элементы, можно конструировать более сложные операции. Если запастись терпением, можно нарисовать граф потока и написать программу для возведения в квадрат – SQUARE – числа из регистра 7, или программу для вычисления среднего – FIND THE AVERAGE – содержимого регистров 1–20, или программу для разложения на множители – FACTOR – содержимого регистра 6 и помещения 1 в регистр 5, если 5 – искомый простой множитель, или программу сравнения – COMPARE – содержимого регистра 3 и регистра 4 и помещения большего содержимого в регистр 5, если только – UNLESS – оно не ровно в два раза больше, потому что в таком случае необходимо поместить метку в регистр 7. И так далее.
Особенно полезна программа, которая будет осуществлять поиск – SEARCH – по содержимому регистров, чтобы проверить, есть ли среди них регистр с конкретным содержимым, и поместить адрес этого регистра в регистр 101. (Как она будет работать? Поместите искомое число – TARGET – в регистр 102, а копию искомого числа – в регистр 103. Обнулите регистр 101, а затем, начиная с регистра 1, вычитайте содержимое регистров из содержимого регистра 103 [после инкрементирования регистра 101], ища нулевую разность. Если регистр 1 не дал нулевой разницы, переходите к регистру 2 и так далее. Если в каком-либо из регистров найдется искомое число, остановите программу; адрес этого регистра окажется в регистре 101.) Благодаря примитивной “чувствительности”, заключенной в инструкции Деп, – ее способности “замечать” нули, когда она пытается декрементировать регистр, – “глаза” регистровой машины можно обратить на нее саму, чтобы она изучала собственные регистры, перемещала между ними содержимое и меняла операции в зависимости от того, что и где она обнаруживает.
секрет 3. Поскольку число в регистре может означать что угодно, регистровая машина, в принципе, может быть сконструирована таким образом, чтобы “замечать” что угодно, или “отличать” любой признак либо черту, которую можно связать с числом – или несколькими числами.
К примеру, черно-белое изображение – любое черно-белое изображение, включая изображение этой страницы, – может быть представлено в виде огромного количества регистров, по одному регистру на пиксель, где 0 означает белую точку, а 1 – черную. Теперь напишите для регистровой машины программу, которая будет искать среди тысяч изображений изображение прямой черной горизонтальной линии на белом фоне. (Не пытайтесь сделать это на самом деле. Жизнь коротка. Просто более или менее живо представьте весь сложный и трудоемкий процесс, который справится с этой задачей.) Сконструировав – в воображении – определитель горизонтальных линий, определитель вертикальных линий и определитель полуокружностей, представьте, как скомпоновать эти фрагменты с несколькими другими полезными распознавателями (возможно, их понадобятся десятки) и написать программу, которая будет находить (заглавную) букву “А” в сотнях разных шрифтов! Программы оптического распознавания символов (OCR) – один из относительно недавних триумфов компьютерного программирования – могут сканировать печатные страницы и достаточно точно преобразовывать их в текстовый файл (в котором каждый буквенный или численный символ представлен числом в кодировке ASCII, так что по тексту можно осуществлять поиск, а также подвергать его другим чудесам текстовой обработки, не используя ничего, кроме арифметики.) Может ли программа OCR читать? Не то чтобы. Она не понимает, что видит. Она вроде как читает, и это удивительно полезная способность, которую можно добавить в нашу богатую коллекцию структурных элементов.
секрет 4. Поскольку число может означать что угодно, оно может означать инструкцию или адрес.
Числом в регистре можно обозначать инструкцию, например ADD, SUBTRACT, MOVE или SEARCH, и адреса (регистров в компьютере), поэтому мы можем хранить всю последовательность инструкций в ряде регистров. Если наша основная программа (программа А) велит машине переходить от регистра к регистру, выполняя содержащиеся в регистре инструкции, тогда в эти регистры можно поместить и вторую программу, программу Б. Когда машина начинает выполнение программы А, первым делом она обращается к регистрам, которые велят ей выполнять программу Б, что машина и делает. Это означает, что можно раз и навсегда поместить программу А в центральный блок обработки данных регистровой машины, зарезервировав для нее ряд регистров (она может стать “встроенной программой”, вшитой в ПЗУ – постоянное запоминающее устройство), а затем использовать программу А, чтобы запускать программы Б, В, Г и так далее, в зависимости от того, какие числа мы помещаем в обычные регистры. Устанавливая программу А на нашу регистровую машину, мы превращаем эту машину в компьютер с хранимой в памяти программой.
Программа А наделяет регистровую машину способностью добросовестно выполнять любые инструкции, которые мы помещаем (по номерам) в регистры. Любая подлежащая выполнению программа состоит из упорядоченной последовательности чисел, к которым по порядку обращается программа А, исполняющая инструкции, обозначенные этими числами. Если разработать систему, которая будет унифицировать эти инструкции (к примеру, присваивать им имена одинаковой длины – скажем, двузначные), можно будет считать всю серию чисел, составляющих программу Б, скажем
86, 92, 84, 29, 08, 50, 28, 54, 90, 28, 54, 90
одним большим и длинным числом:
869284290850285490285490
Это число одновременно представляет собой уникальное “имя” программы, программы Б, и саму программу, которая пошагово выполняется программой А. Вот другая программа:
28457029759028752907548927490275424850928428540423
и третья:
8908296472490284952498856743390438503882459802854544254789653985,
но самые интересные программы имеют гораздо более длинные имена, включающие миллионы знаков. Программы, хранимые в памяти вашего ноутбука, например текстовый процессор и браузер, представляют собой именно такие длинные числа, состоящие из многих миллионов (двоичных) знаков. Программа размером 10 мегабит – это последовательность из восьмидесяти миллионов нулей и единиц.
секрет 5. Всем возможным программам в качестве имени может быть присвоено уникальное число, которое затем можно считать списком инструкций для универсальной машины.
Блестящий теоретик и философ Алан Тьюринг вывел эту схему, используя другой простой воображаемый компьютер, который движется по разделенной на ячейки бумажной ленте. Поведение этого компьютера зависит (ага! – условный переход) от того, считывает он ноль или единицу из той ячейки, которую обрабатывает в данный момент. Машина Тьюринга умеет только менять бит (стирать 0, записывать 1 – и наоборот) или оставлять бит нетронутым, а затем перемещаться влево или вправо на одну ячейку и переходить к следующей инструкции. Думаю, вы согласитесь, что создание программ сложения, вычитания и других функций для машины Тьюринга при использовании только двоичных чисел 0 и 1 вместо всех натуральных чисел (0, 1, 2, 3, 4, 5 и т. д.) и перемещении лишь на одну ячейку зараз – гораздо более трудоемкий процесс, чем наши упражнения с регистровой машиной, но смысл при этом одинаков. Универсальная машина Тьюринга – это устройство с программой А (если хотите, встроенной), которая позволяет ему “считывать” программу Б с бумажной ленты и затем выполнять ее, используя остальную информацию с ленты в качестве вводных данных для программы Б. Регистровая машина Хао Вана способна выполнить любую программу, которую можно свести к арифметике и условным переходам, и таковы же возможности машины Тьюринга. Обе машины обладают чудесной способностью брать номер любой другой программы и выполнять этот номер. Вместо того чтобы конструировать сотни разных вычислительных машин, каждая из которых будет прошита для выполнения конкретной сложной задачи, достаточно создать единственную многоцелевую универсальную машину (с предустановленной программой А) и заставить ее исполнять наши запросы, пополняя ее программами – программным обеспечением, – создающими виртуальные машины.
Иными словами, универсальная машина Тьюринга представляет собой универсальный имитатор. То же самое можно сказать и о менее известной универсальной регистровой машине. И о вашем ноутбуке. Ваш ноутбук не делает ничего такого, что не могла бы сделать универсальная регистровая машина, и наоборот. Но не обольщайтесь. Никто не говорит, что все машины работают с одинаковой скоростью. Мы увидели, как ужасно медленно наша регистровая машина выполняет такую кропотливую операцию, как деление, которое она – мама дорогая! – осуществляет путем последовательного вычитания. Неужели нет способа ускорить процесс? Конечно есть. Фактически история компьютеров со времен Тьюринга до сегодняшнего дня – это как раз история поиска все более быстрых способов делать то, что делает регистровая машина, и ничего более.
секрет 6. Все усовершенствования компьютеров с момента изобретения воображаемой машины Тьюринга, движущейся по бумажной ленте, просто ускоряют их работу.
К примеру, Джон фон Нейман создал архитектуру для первого серьезного работающего компьютера, и чтобы ускорить его работу, он расширил окно головки записи-чтения машины Тьюринга, чтобы она читала зараз не один бит, а много. Многие ранние компьютеры читают 8-битные, 12-битные и даже 16-битные “слова”. Сегодня часто используются 32-битные слова. Это все еще узкое место – узкое место фон Неймана, – но оно в 32 раза шире узкого места машины Тьюринга! Прибегнув к некоторому упрощению, можно сказать, что слова по очереди копируются – COPY – из памяти в особый регистр (регистр инструкции), где эта инструкция читается – READ – и исполняется. Как правило, слово состоит из двух частей, кода операции (например, ADD, MULTIPLY, MOVE, COMPARE, JUMP-IF-ZERO) и адреса, который говорит компьютеру, к какому регистру обращаться за содержимым для проведения операции. Таким образом, 10101110 11101010101 может говорить компьютеру выполнять операцию 10101110 на содержимом регистра 11101010101, всегда помещая ответ в специальный регистр, называемый аккумулятором. Существенное различие между регистровой машиной и машиной фон Неймана заключается в том, что регистровая машина может осуществлять операции на любом регистре (само собой, только операции Инк и Деп), а машина фон Неймана выполняет всю арифметическую работу в аккумуляторе и просто копирует и перемещает – COPY и MOVE – содержимое в регистры памяти (или накапливает его – STORE – в этих регистрах). Все эти дополнительные перемещения и копирования окупаются возможностью осуществлять большое количество аппаратно-реализованных базовых операций. Иначе говоря, существует одна электронная схема для операции ADD, другая – для операции SUBTRACT, третья – для операции JUMP-IF-ZERO и так далее. Код операции напоминает код города в телефонной системе или индекс в почтовом адресе: он отправляет то, над чем работает, в верное место для исполнения. Так программное обеспечение встречается с аппаратным.
Сколько примитивных операций содержится сегодня в настоящих компьютерах? Сотни и даже тысячи. Кроме того, как в старые добрые времена, компьютер может быть наделен сокращенным набором команд (работать на архитектуре RISC): такой компьютер умеет выполнять лишь несколько десятков примитивных операций, но при этом работает молниеносно. (Если инструкции Инк и Деп можно исполнять в миллион раз быстрее, чем аппаратно-реализованную операцию ADD, будет целесообразно составить программу ADD, используя Инк и Деп, как мы делали ранее, и для всех операций сложения, предполагающих менее миллиона шагов, мы останемся в выигрыше.)
Сколько регистров содержится сегодня в настоящих компьютерах? Миллионы и даже миллиарды (но все они конечны, так что огромные числа должны распределяться по большому числу регистров). Байт состоит из 8 бит. Имея на своем компьютере 64 мегабайта RAM (оперативной памяти), вы имеете шестнадцать миллионов 32-битных регистров – или их эквивалент. Мы знаем, что содержимое регистров может обозначать не только положительные целые числа. Действительные числа (например, π, √2 или ⅓) хранятся в форме чисел “с плавающей запятой”. Эта форма представления разбивает число на две части, мантиссу и порядок, как в экспоненциальной записи (“1,495 × 1041”), что позволяет компьютеру производить арифметические действия, чтобы работать с числами (в приближенном представлении), которые натуральными не являются. Операции с плавающей запятой – это обычные арифметические операции (в частности, умножение и деление) над числами с плавающей запятой, и самый быстрый суперкомпьютер, который можно было купить двадцать лет назад (когда я написал первую версию этой главы), имел производительность более 4 мегафлопс (от англ. floating point operations per second), то есть мог выполнять более 4 миллионов операций с плавающей запятой в секунду.
Если вам этого мало, можно параллельно подключить друг к другу большое количество таких машин, чтобы все они работали одновременно, а не последовательно, не ожидая в очереди результатов для их последующей обработки. Функционал параллельного компьютера не отличается от функционала последовательного компьютера, но работает он быстрее. Фактически большинство параллельных машин, изучавшихся в последние двадцать лет, было виртуальными машинами, смоделированными на стандартных (непараллельных) машинах фон Неймана. Было разработано параллельное аппаратное обеспечение особого назначения, а конструкторы вычислительных машин изучают стоимость и перспективы расширения узкого места фон Неймана и ускорения проходящего сквозь него трафика всевозможными способами – с использованием сопроцессоров, кэш-памяти и различных других подходов. Сегодня японский компьютер Fujitsu K имеет производительность 10,51 петафлопс, то есть более десяти тысяч триллионов операций с плавающей запятой в секунду.
Возможно, этого почти достаточно, чтобы смоделировать вычислительную активность вашего мозга в реальном времени. Ваш мозг – образцовый параллельный процессор, имеющий около сотни миллиардов нейронов, каждый из которых представляет собой сложного маленького агента, имеющего конкретную задачу. Полоса пропускания зрительного “нерва”, по которому визуальная информация передается из глаза в мозг, составляет несколько миллионов каналов (нейронов). Но нейроны работают гораздо медленнее компьютерных микросхем. Нейрон может изменить состояние и отправить сигнал (фактически свою вариацию инструкции Инк или Деп) за несколько миллисекунд – тысячных, а не миллионных и не миллиардных долей секунды. Компьютеры перемещают биты со скоростью, близкой к скорости света, поэтому чем меньше компьютер, тем быстрее он работает: свет преодолевает 30 см примерно за одну миллиардную долю секунды, поэтому если вы хотите, чтобы два процесса коммуницировали быстрее, они должны проистекать ближе друг к другу.
секрет 7. Больше секретов нет!
Вероятно, самое удивительное свойство компьютеров заключается в том, что они составляются – простыми шагами – из элементов (операций), которые также предельно просты, а потому им просто негде хранить секреты. В них нет ни эктоплазмы, ни “морфических резонансов”, ни невидимых силовых полей, ни неизвестных прежде законов физики, ни чудо-ткани. Вы знаете, что если вы сумели написать компьютерную программу, которая моделирует какой-либо феномен, то эта модель не задействует ничего, кроме различных конфигураций арифметических операций.
Что насчет квантовых компьютеров, которые сейчас на пике популярности? Разве квантовые компьютеры умеют что-то такое, что не умеют обычные? И да и нет. Они умеют одновременно решать множество задач и вычислять множество значений, благодаря “квантовой суперпозиции”, причудливому и необычному свойству, которое гласит, что ненаблюдаемая сущность может одновременно пребывать во “всех возможных” состояниях, пока наблюдение не приведет к “коллапсу волновой функции”. (Подробнее об этом почитайте в своей любимой научно-популярной книге по физике или на познавательном сайте.) По сути, квантовый компьютер не что иное, как последняя и весьма впечатляющая инновация – можно сказать, квантовый скачок – в скорости обработки данных. Машина Тьюринга, движущаяся по бумажной ленте, и регистровая машина, неутомимо инкрементирующая и декрементирующая отдельные регистры, крайне ограничены в том, что они могут сделать за короткое время – минуты, часы или дни. Суперкомпьютер вроде Fujitsu K может делать все то же самое в триллионы раз быстрее, но для решения некоторых задач, особенно из области криптографии, этой скорости все равно недостаточно. Именно в этой сфере может пригодиться сверхбыстрый квантовый компьютер – если, конечно, люди сумеют решить невероятно сложные инженерные проблемы, возникающие при попытке создания стабильного и практичного квантового компьютера. Возможно, создать его так и не удастся, и тогда нам придется довольствоваться какими-то квадриллионами флопс.
Назад: IV. Интерлюдия о компьютерах
Дальше: 25. Виртуальные машины

