95
Собственное значение уравнения для оператора объема.
96
Поскольку квантовые состояния гравитации выражаются как, где n относится к узлам, а l – к ребрам графа.
97
Результат расчета прост. Я продемонстрирую его здесь, чтобы вы увидели, как работает дираковский спектр. Возможные значения площади A даются следующей формулой, где j принимает полуцелые значения, то есть 0, 1/2, 1, 3/2, 2, 5/2, 3…
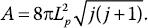
Здесь A – площадь, которую может иметь поверхность, разделяющая два «зерна» пространства; 8 – это обычное число восемь, ничего особенного; π – греческая буква пи, которая, как мы учили в школе, означает отношение длины любой окружности к ее диаметру; эта величина почему-то постоянно появляется в разных разделах физики. Lp – это планковская длина, то есть предельно малый размер, на котором проявляются эффекты квантовой гравитации. L2p – это квадрат величины Lp, который соответствует (чрезвычайно малой) площади крошечного квадрата со сторонами, равными планковской длине. Таким образом, 8πL2p – это просто «маленькая» площадь, площадь микроскопического квадрата со стороной примерно в одну миллионную миллиардной миллиардной миллиардной доли сантиметра (10–66 см2). Интересная особенность этой формулы – квадратный корень в ней. Ключевой момент здесь – то, что j принимает полуцелые значения, то есть кратные 1/2. Например, для каждого из них данный корень приобретает определенные значения, которые в приближенном виде даны в табл. 6.1.
Таблица 6.1. Спин (полуцелый) и соответствующие значения площади в единицах минимальной площади

Умножая числа из правой колонки на площадь 8πL2p, мы получаем возможные значения площади поверхности. Эти особые значения подобны тем, что появляются при изучении орбит электронов в атомах, где квантовая механика допускает лишь определенные орбиты. Ключевой момент состоит в том, что не существует никаких других площадей, кроме тех, значения которых выводятся из этого уравнения. Никакая поверхность не может иметь площадь в одну десятую 8πL2p.

