Механика 7. Шанс
Седьмая и последняя игровая механика – это шанс. Мы разбираем ее в последнюю очередь, потому что она касается взаимодействий между остальными шестью механиками: пространством, временем, объектами, действиями, правилами и навыками.
Шанс является неотъемлемой частью увлекательной игры, ведь он подразумевает неопределенность, а неопределенность подразумевает сюрпризы. И, как мы уже выяснили ранее, сюрпризы являются важным источником человеческого удовольствия и секретным ингредиентом фана.
С этого момента мы должны двигаться осторожно. Если не хотите обмануться, никогда не воспринимайте шанс как должное. Он представляет собой следствие сложных математических расчетов, поэтому полагаться на интуицию не стоит. Но хороший геймдизайнер должен стать хозяином шанса и вероятности, подчиняя их своей воле и создавая опыт, наполненный напряженными решениями и интересными сюрпризами. Проблемы понимания шанса отлично проиллюстрированы в рассказе об изобретении в математике такого понятия, как вероятность, которая, что совсем неудивительно, повсеместно применяется в геймдизайне.
Изобретение Вероятности
Он отличный парень, но, к сожалению, не математик.Паскаль Ферма о шевалье де Мере
Шел 1654 год, а у французского дворянина Антуана Гомбальда, шевалье де Мере, была проблема – он был заядлым игроком. Он раз за разом ставил на то, что при броске одного игрального кубика четыре раза подряд хотя бы один раз выпадет шестерка. На этой игре он заработал неплохие деньги, но его друзьям надоело проигрывать, и впредь они отказывались с ним играть. В поисках новых способов обобрать своих друзей шевалье изобрел еще одну игру, которая, как он считал, использовала то же правило вероятности, что и предыдущая. В новой игре он ставил на то, что при броске двух кубиков двадцать четыре раза подряд один раз выпадет двенадцать. Сначала друзья отнеслись к новой игре с подозрением, но вскоре она начала им нравиться, ведь шевалье стремительно терял свои накопления! Он не мог понять, что происходит, ведь, по его подсчетам, обе игры использовали одно и то же правило вероятности. Обоснование шевалье было следующим:
Первая игра: бросая одну кость четыре раза, шевалье выигрывал, если выпадала по крайней мере одна шестерка.
Шевалье объяснял, что вероятность выпадения 6 на одной кости равняется 1/6 и поэтому, если он бросит кость четыре раза, шанс на выигрыш будет
4 × (1/6) = 4/6 = 66 %, что объясняет, почему он так часто побеждал.
Вторая игра: бросая две кости двадцать четыре раза, шевалье выигрывал, если по крайней мере один раз выпадало 12.
Шевалье посчитал, что шанс выпадения 12 (две шестерки) на двух костях равен 1/36. Затем он пришел к тому, что, если бросить кости 24 раза, вероятность будет следующей:
24 × (1/36) = 24/36 = 2/3 = 66 %. Та же вероятность, что и в первой игре.
Запутавшийся и разоренный, он написал письмо математику Блезу Паскалю, у которого попросил совета. Паскаль нашел проблему интригующей – официальная математика не могла ответить на эти вопросы. И тогда Паскаль обратился за помощью к другу своего отца, Пьеру де Ферма. Это положило начало долгой переписке между Паскалем и Ферма, в которой они обсуждали эту и другие похожие проблемы, пытались найти методы их решения и в итоге основали новый раздел математики – теорию вероятности.
Так каковы же реальные шансы в играх шевалье? Чтобы это понять, нам потребуются математические познания – не волнуйтесь, это простая математика, понятная всем. Всецело погружаться в теорию вероятности геймдизайнеру не нужно, но ее основы могут вам пригодиться. Если вы математический гений, можете пропустить эту часть или по крайней мере не сильно в нее вдумываться. А для всех остальных я представляю:
Правила вероятности, которые должен знать каждый геймдизайнер
Правило 1: Дроби и проценты
Если вы – один из тех, кто никогда не ладил с дробями и процентами, пришло время столкнуться с ними лицом к лицу и победить, потому что они являются языком вероятности. Не переживайте – всегда можно воспользоваться калькулятором, никто не смотрит. Вам нужно понять, что простые дроби, десятичные дроби и проценты – это все одно и то же, то есть они взаимозаменяемы. Иными словами, ½ = 0,5 = 50 %. Это не разные числа, это просто разные способы записать одно и то же число.
Переводить простые дроби в десятичные очень просто. Нужен десятичный эквивалент 33/50? Просто разделите 33 на 50 на калькуляторе, и вы получите 0,66. А что делать с процентами? С ними тоже все просто. Если вы поищете слово Percent в словаре, то увидите, что буквально это означает «на 100» (per 100). Значит, 66 % на самом деле означает 66 на 100, или 66/100, или 0,66. Если посмотреть на подсчеты шевалье, можно понять, зачем нужно так часто переводить числа – людям свойственно говорить на языке процентов, но мы так же часто говорим «один шанс из шести» – так что мы должны уметь сопоставлять эти формулировки. Если у вас никогда не ладилось с математикой, просто расслабьтесь и попрактикуйтесь немного с калькулятором, и вы сразу всему научитесь.
Правило 2: От нуля до единицы – вот и все!
Тут все предельно просто. Вероятность может быть только от 0 до 100 %, то есть от 0 до 1 (смотри правило 1), не больше и не меньше. Мы можем сказать, что что-то случится с вероятностью 10 %, но вероятности –10 % или 110 % не существует. 0 % вероятности события означает, что это событие точно не произойдет, 100 % – что определенно случится. Все это может показаться очевидным, но именно такие очевидные вещи были основной проблемой подсчетов шевалье. Давайте посмотрим на его первую игру. Он был уверен в том, что, бросая одну кость четыре раза, он имел шанс, равный 4 × (1/6), или 4/6, или 0,66, или 66 %, на то, что выпадет шестерка. А если бы он бросал кость семь раз? Тогда у него получилась бы вероятность, равная 7 × (1/6), или 7/6, или 1,17, или 117 %! А такого определенно не могло быть – если вы бросаете кость семь раз, вероятно, что шестерка все-таки выпадет один раз, но вы не можете быть в этом уверены (на самом деле, шанс равен приблизительно 72 %). Если при расчете вероятности у вас получается число больше, чем 100 % (или меньше, чем 0 %), можете быть уверены: вы что-то сделали не так.
Правило 3: «Искомое значение», разделенное на «возможные результаты», равняется вероятности
Первые два правила описывают лишь основы, но теперь пришло время поговорить о том, чем на самом деле является вероятность, – и в этом нет ничего сложного. Вы просто берете количество «желаемых» результатов и делите его на количество возможных результатов (при условии, что результаты равновозможные), и вот у вас уже есть вероятность. Каков шанс выпадения шестерки, когда вы бросаете кость? Так, у нас есть шесть возможных результатов и один желаемый, значит, шанс получить шестерку равен 1/6, или около 17 %. Какой шанс, что выпадет парное число, когда вы бросаете кость? На кубике 3 парных числа, а это значит, что ответ 3/6, или 50 %. Каков шанс вытащить из колоды «фигурную» карту (валет, дама, король)? В колоде есть 12 фигурных карт, а всего в ней 52 карты, значит, шанс вытянуть фигурную карту равняется 12/52, или 23 %. Если вы понимаете это, вы понимаете основы вероятности.
Правило 4: Перечисляйте!
Если правило 3 такое простое, каким кажется на первый взгляд (а так оно и есть), то почему же тогда вероятность такая сложная? Причина кроется в том, что те два числа, которые нам нужны (число «желаемых» результатов и число ожидаемых результатов), не всегда бывают очевидными. Например, если я спрошу вас, каким будет шанс выпадения по крайней мере двух «орлов» при трех попытках подбрасывания монеты и каким в этом случае будет число «желаемых» результатов? Я бы удивился, если бы вы смогли ответить на этот вопрос, не делая никаких записей. Самый простой способ решить эту задачу – перечислить все возможные результаты.
1. ООО
2. ООР
3. ОРО
4. ОРР
5. РОО
6. РОР
7. РРО
8. РРР
Как видим, у нас есть восемь возможных результатов. В каких из них «орел» выпадает по крайней мере дважды? 1, 2, 3 и 5. Это четыре результата из восьми возможных, то есть ответ – 4/8, или 50 %. Но почему тогда у шевалье не получилось сделать то же со своими играми? В первой игре он бросал кость четыре раза, что означает 6 × 6 × 6 × 6, или 1296 возможных вариантов. Перечислить все возможные результаты – довольно скучное занятие, но, если взяться за него, можно управиться примерно за час (список выглядел бы примерно так: 1111, 1113, 1114, 1115, 1116, 1121, 1122, 1123 и т. д.), плюс еще пара минут на то, чтобы посчитать количество комбинаций, содержащих шестерки (671). И в конце разделить это количество на 1296, чтобы получить ответ на свой вопрос. Подобный подсчет поможет вам решить любую проблему, связанную с вероятностью, если у вас, конечно, есть на это время. А теперь давайте взглянем на вторую игру, где шевалье бросал две кости 24 раза. Для двух костей существуют 36 возможных результатов, то есть, посчитав количество результатов при 24 бросках, нам нужно будет записать количество комбинаций, равное 36 в 24-й степени (число, состоящее из 37 цифр). Даже если шевалье смог бы писать по одной комбинации в секунду, составление такого списка заняло бы больше времени, чем возраст самой Вселенной. Перечисление может быть очень удобным подходом, но, если оно занимает чересчур много времени, нужно искать иные пути – именно для этого нужны следующие правила.
Правило 5: В некоторых случаях «или» означает сложение
Очень часто нам нужно определить шанс «того ИЛИ иного» события, например какой шанс вытащить из колоды фигурную карту ИЛИ туз? Когда два события, о которых мы говорим, являются взаимоисключающими, иными словами, когда они оба не могут произойти одновременно, вы можете сложить их индивидуальные вероятности, чтобы получить общую вероятность. Например, шанс вытянуть фигурную карту составляет 12/52, а шанс вытянуть туз – 4/52. Поскольку эти события взаимоисключающие (они не могут произойти одновременно), мы можем их суммировать: 12/52 + 4/52 = 16/52, или около 31 % вероятности.
Но что, если задать другой вопрос: каковы шансы вытащить из колоды туз или бубну? Если суммировать эти вероятности, мы получаем 4/52 + 13/52 (13 бубновых карт в колоде) = 17/52. Но если мы перечислим результаты, то увидим, что это неправильный ответ; правильный ответ – 16/52. Почему? Потому что эти два случая не являются взаимоисключающими – я могу вытащить бубновый туз! Поскольку этот случай не взаимоисключающий, «или» не означает сложение.
Давайте посмотрим на первую игру шевалье. Кажется, что он использует это правило для своих костей – сложение вероятностей: 1/6 + 1/6 + 1/6 + 1/6. Но он получает неправильный ответ, потому как эти четыре события не взаимоисключающие. Правило сложения весьма полезное, но только если вы уверены в том, что события являются взаимоисключающими.
Правило 6: В некоторых случаях «и» означает умножение
Это правило практически противоположно предыдущему! Если мы хотим знать, чему равняется вероятность двух происходящих одновременно событий, для получения ответа мы можем умножить их вероятности – но только если эти два события НЕ взаимоисключающие! Возьмем две игральные кости. Если мы хотим узнать вероятность выпадения двух шестерок, нам нужно умножить вероятность двух событий: шанс получить 6 на одной кости равняется 1/6, а также шанс получить 6 на второй кости, который тоже равняется 1/6. Выходит, что шанс выпадения двух шестерок – 1/6 × 1/6 = 1/36. Вы могли бы одинаково успешно прийти к этому выводу путем перечисления, но это отняло бы у вас намного больше времени. В правиле 5 мы пытались узнать вероятность вытянуть туз ИЛИ бубну из колоды – правило не подействовало, потому что эти события не были взаимоисключающими. Теперь давайте попробуем узнать вероятность вытащить туза И любую карту бубновой масти. Иными словами, какая вероятность вытащить бубнового туза? Интуитивно мы понимаем, что этот шанс равен 1/52, но мы можем проверить это при помощи правила 6, поскольку знаем, что оба события не являются взаимоисключающими. Шанс вытащить туза равняется 4/52, а шанс вытащить бубну – 13/52. Умножим их: 4/52 × 13/52 = 52/2704 = 1/52. То есть правило работает и соответствует нашим умозаключениям.
Достаточно ли нам этих правил, чтобы решить проблему шевалье? Давайте взглянем на первую игру.
Первая игра: бросая одну кость четыре раза, шевалье выигрывал, если выпадала по крайней мере одна шестерка.
Мы уже пришли к тому, что могли пересчитать все результаты и получить ответ 671/1296, но это заняло бы целый час. Можно ли сделать это быстрее, используя те правила, которые мы уже знаем?
(Я хочу вас предупредить: дальше все будет несколько сложнее. Если вам это не сильно нужно, избавьте себя от лишней головной боли и просто пропустите правило 7. Если вам действительно интересна разгадка, приготовьтесь – оно того стоит.)
Если бы вопрос был о том, каковы шансы выпадения четырех шестерок при кидании одной кости четыре раза, это был бы вопрос с «И» для четырех не взаимоисключающих событий, что позволило бы нам обойтись правилом 6: 1/6 × 1/6 × 1/6 × 1/6 = 1/1296. Но в нашей задаче другое условие. Перед нами стоит вопрос с «ИЛИ» для четырех не взаимоисключающих событий (возможно, что шевалье получит больше, чем одну шестерку за четыре броска). Так что же нам делать? Первый способ – выделить взаимоисключающие события и суммировать их. Но есть и другой способ описать словами эту игру.
Какой шанс бросить кость и получить следующие результаты:
1. Четыре шестерки, ИЛИ
2. Три шестерки и одна не-шестерка, ИЛИ
3. Две шестерки и две не-шестерки, ИЛИ
4. Одна шестерка и три не-шестерки?
Звучит сложновато, но мы имеем четыре взаимоисключающих события, и, если сможем узнать вероятность каждого из них, то сможем просто суммировать их и получить ответ на свой вопрос. Мы уже узнали вероятность события 1, используя правило 6: 1/1296. А что насчет 2? На самом ли деле 2 – это четыре разных взаимоисключающих события:
a) 6, 6, 6, не-шесть;
b) 6, 6, не-шесть, 6;
c) 6, не-шесть, 6, 6;
d) не-шесть, 6, 6, 6?
Вероятность выпадения шестерки равна 1/6, а вероятность выпадения не-шестерки – 5/6. То есть вероятность каждого из этих событий – 1/6 × 1/6 × 1/6 × 5/6 = 5/1296. Теперь, если суммировать все четыре, получается 20/1296. Выходит, что вероятность 2 – 20/1296.
Что насчет 3? Здесь все так же, как и в предыдущем случае, но с большим количеством комбинаций. Сложно посчитать точное количество комбинаций с двумя шестерками и двумя не-шестерками, но эта цифра равна шести:
a) 6, 6, не-шесть, не-шесть;
b) 6, не-шесть, 6, не-шесть;
c) 6, не-шесть, не-шесть, 6;
d) не-шесть, 6, 6, не-шесть;
e) не-шесть, 6, не-шесть, 6;
f) не-шесть, не-шесть, 6, 6.
И вероятность каждой из них – 1/6 × 1/6 × 5/6 × 5/6 = 25/1296. Суммируем все шесть и получаем 150/1296.
Осталось только 4, что является противоположностью 1:
a) не-шесть, не-шесть, не-шесть, 6;
b) не-шесть, не-шесть, 6, не-шесть;
c) не-шесть, 6, не-шесть, не-шесть;
d) 6, не-шесть, не-шесть, не-шесть.
Вероятность каждого из вариантов – 5/6 × 5/6 × 5/6 × 1/6 = 125/1296. Складываем все четыре и получаем 500/1296.
Выходит, мы высчитали вероятность для четырех взаимоисключающих событий:
1. Четыре шестерки – (1/1296);
2. Три шестерки и одна не-шестерка – (20/1296);
3. Две шестерки и две не-шестерки – (150/1296);
4. Одна шестерка и три не-шестерки – (500/1296).
Суммируя эти четыре вероятности (в соответствии с правилом 5), мы получаем общую вероятность 671/1296, или около 51,77 %. Таким образом, мы можем видеть, насколько выгодной была эта игра для шевалье. Побеждая чаще, чем в 50 % случаев, он в конечном счете имел неплохие шансы на выигрыш, но вероятность была достаточно близка к середине, чтобы его друзья верили, что у них был шанс победить, – по крайней мере какое-то время. Но этот результат определенно отличается от тех 66 %, на которые рассчитывал шевалье.
Тот же ответ мы могли бы получить путем перечисления, но это заняло бы слишком много времени. Некое перечисление все же имело место, но правила сложения и умножения позволяют нам перечислять все намного быстрее. Сможем ли мы таким путем получить ответ на вопрос о второй игре шевалье? Можем, но с 24 бросками двух костей мы потратили бы на это больше часа. Такой подход определенно быстрее перечисления, но, если проявить немного смекалки, можно еще ускорить процесс – и здесь на помощь приходит правило 7.
Правило 7: Один минус «да» = «нет»
Это больше интуитивное правило. Если шанс какого-то события равен 10 %, то шанс, что это событие не произойдет, – 90 %. Почему это полезно? Потому что иногда вычислить вероятность возникновения какого-то события сложнее, чем вероятность того, что оно НЕ произойдет.
Посмотрим на вторую игру шевалье. Вычислить вероятность выпадения по крайней мере одной двойной шестерки при 24 бросках было бы крайне трудно потому, что тогда бы нам пришлось сложить слишком много событий (1 двойная шестерка, 23 не-шестерки, 2 двойные шестерки, 22 не-шестерки и т. д.). Но что, если мы поставим вопрос иначе: какой шанс бросить две кости двадцать четыре раза и НЕ выбросить ни одной двойной шестерки? Теперь это вопрос с «И» для не взаимоисключающих событий, так что мы можем применить правило 6, чтобы узнать ответ. Но сначала мы еще два раза используем правило 7 – смотрите.
Шанс, что двойная шестерка выпадет после одного броска, равен 1/36. Итак, согласно правилу 7, вероятность того, что двойная шестерка не выпадет, – 1 – 1/36, или 35/36.
То есть, если применить правило 6 (умножение), шанс на то, что двойная шестерка не выпадет ни разу при 24 бросках, составит 35/36 × 35/36 двадцать четыре раза, или, чтобы было понятнее, 35/36 в 24-й степени. Вы вряд ли захотите делать все эти подсчеты вручную, но если взять калькулятор, то вы увидите, что ответ – 0,5086, или 50,86 %. Но это вероятность проигрыша шевалье. Чтобы вычислить вероятность его выигрыша, нам нужно применить правило 7 еще раз: 1 – 0,5086 = 49,14 %. Теперь понятно, почему он проигрывал. Шанс на победу был настолько близким к половине, что его трудно было отличить от шанса на поражение, но после большого количества игровых сессий стало понятно, что поражение было более вероятным исходом.
Несмотря на то что все вопросы, связанные с вероятностью, можно решить посредством перечисления, правило 7 поможет вам сохранить много времени. На самом деле, это же правило мы могли бы применить и для первой игры шевалье.
Правило 8: Сумма нескольких линейных случайных исходов – это НЕ линейный случайный исход!
Не паникуйте. Как бы сложно это ни звучало, на самом деле все просто. «Линейный случайный исход» – это просто случайное событие, в котором все результаты имеют одинаковую вероятность. Бросание игральной кости – это отличный пример линейного случайного выбора. Хотя, если бросить несколько игральных костей, то возможные результаты НЕ будут иметь одинаковую вероятность. Если вы, например, бросаете две кости, то шанс получить семь довольно высок, в то время как шанс получить 12 намного меньше. Перечислив все возможности, вы поймете, почему так получается:

Посмотрите, как много в этой таблице 7 и всего одно 12! Мы можем продемонстрировать это на диаграмме под названием «Кривая распределения вероятности», чтобы увидеть шансы каждого из результатов.

Правило 8 кажется довольно очевидным, но я часто вижу, как начинающие дизайнеры составляют вместе два случайно выбранных числа, не понимая эффекта этого сложения. А иногда это именно тот эффект, который вам нужен, например, в игре Dungeons and Dragons игрок зарабатывает (виртуальные) очки навыков достоинством от 3 до 18, бросая три обычные (шестигранные) игральные кости. В результате в игре доминируют навыки достоинством 10 или 11, а 3 или 18 встречаются крайне редко, и это именно то, чего хотел дизайнер. А теперь представьте, насколько сильно игра отличалась бы от оригинальной версии, если бы, зарабатывая очки, игроки бросали один двадцатигранный кубик?
Геймдизайнеры, собирающиеся использовать механику шанса как инструмент для создания своих игр, должны понимать, какая кривая распределения вероятности нужна именно им, а также знать, как ее получить. С опытом к вам придет понимание того, насколько ценными инструментами могут быть кривые распределения вероятности.
Правило 9: Бросайте кости
Все вероятности, о которых мы говорили до этого, были теоретическими вероятностями, иными словами, тем, что должно случиться. Существует также практическая вероятность, которая является мерой того, что уже случилось. Например, если бросить кость, теоретическая вероятность выпадения шестерки составит ровно 1/6, или около 16,67 %. Но я мог бы вычислить практическую вероятность, бросив игральную кость 100 раз и записав, сколько раз мне попадались шестерки. Мне могут выпасть 20 шестерок из 100. В этом случае практическая вероятность составит 20 %, что не слишком сильно отличается от теоретической вероятности. Конечно, с увеличением количества попыток практическая вероятность все больше приближается к теоретической. Это правило получило название «метод Монте-Карло» в честь знаменитого казино.
Положительной чертой использования метода Монте-Карло для вероятности является то, что он не требует сложных математических подсчетов – вы проделываете одно и то же действие много раз и просто записываете результаты. Иногда результаты подобных тестов могут быть полезнее теоретической вероятности потому, что здесь мы имеем дело с реальными сущностями. Если существуют факторы, которые нельзя учесть при математических подсчетах (возможно, центр тяжести вашего кубика немного смещен к шестерке), или же эти подсчеты настолько сложные, что вы не можете составить теоретическую картину вашей ситуации, метод Монте-Карло – это то, что вам нужно. Шевалье мог бы легко ответить на свой вопрос, бросая кости снова и снова, считая количество побед и разделяя их на число сделанных попыток.
Сегодня, в компьютерную эру, если вы хоть немного умеете программировать (или знаете того, кто умеет, – смотрите правило 10), вы можете без труда создать симуляцию миллиона попыток всего за несколько минут. На самом деле, это совсем не трудно – написать симуляцию игры и получить ответы на вопросы, касающиеся вероятности. Например, на какую клетку в «Монополии» фишки игроков встают чаще всего? Теоретически это невозможно выяснить – но, используя компьютер и метод Монте-Карло, вы с легкостью выясните это, написав симуляцию бросания кубика и передвижения фишки по игровому полю несколько миллионов раз.
Правило 10: Гики любят хвастаться (Закон Гомбо)
Это самое важное из всех правил вероятности. Вам будет достаточно одного этого правила, даже если вы забудете все остальные. У вероятности есть много сложных аспектов, в подробности которых мы вдаваться не будем, но если вам все же пришлось столкнуться с ними – проще всего найти человека, который считает себя «математическим гением». Обычно этим людям просто необходимо знать, что их помощь кому-то нужна, поэтому они вылезут из кожи вон, лишь бы вам помочь. Я много раз использовал правило 10 для решения самых сложных вопросов геймдизайна, связанных с вероятностью. Если у вас нет знакомых математиков, оставляйте ваши вопросы на специализированных форумах или на других подобных сервисах. Если вы хотите получить быстрый ответ, начните ваш пост фразой «Наверное, эту проблему решить невозможно, но я думаю, что спросить все-таки стоит», потому что многие математики любят поднимать собственную самооценку, решая задачи, которые до них никто решить не смог. Ваша сложная задача для них в некотором смысле игра. Так почему бы не воспользоваться геймдизайнерскими приемами, чтобы сделать ваш пост привлекательнее?
Возможно, вы даже окажете этим услугу своему гику! Я называю правило 10 Законом Гомбо, в честь Антуана Гомбо, шевалье де Мере, который, пользуясь этим принципом, не только решил свою игровую проблему, но и непреднамеренно положил начало теории вероятности.
Некоторые не применяют правило 10, боясь задавать глупые вопросы. Если это ваш случай, вспомните, что Паскаль и Ферма находятся в большом долгу перед шевалье – без его глупых вопросов они бы никогда не сделали своих фундаментальных открытий. Ваш глупый вопрос может привести к рождению грандиозной истины, но вы никогда не узнаете об этом, если не попробуете его задать.
Ожидаемое значение
В вашем дизайне вам придется по-разному использовать вероятность, но полезнее всего будет подсчитать ожидаемое значение. Очень часто каждое ваше действие в игре имеет значение, которое может быть либо позитивным, либо негативным. Это могут быть очки, медали, деньги, которые вы можете получить или потерять. Ожидаемое значение в игре – это среднее арифметическое всех возможных значений, присущих конкретной игре.
Например, в настольной игре может быть правило, согласно которому ступающий на зеленое поле игрок может бросить кубик и получить количество очков, соответствующее значению на нем. Ожидаемое значение этого события – это среднее арифметическое всех возможных результатов. Чтобы узнать среднее арифметическое в этом случае, при условии что все вероятности тождественны, мы можем сложить все возможные значения игральной кости: 1 + 2 + 3 + 4 + 5 + 6 = 21, что, разделенное на 6, дает нам результат 3,5. Как геймдизайнеру, вам очень важно знать, что каждый раз, когда кто-то оказывается на зеленом поле, он в среднем зарабатывает 3,5 очка.
Но не все примеры такие простые – в некоторых встречаются негативные результаты или результаты, которые не являются равновозможными. Возьмем игру, где игрок бросает два кубика. Если на кубиках выпадает 7 или 11, игрок получает 5 долларов, но, если выпадает что-то другое, он теряет 1 доллар. Как мы можем вычислить ожидаемое значение для этой игры?
Шанс выпадения 7 – 6/36.
Шанс выпадения 11 – 2/36.
Согласно правилу 8 шанс всех остальных результатов – 1 – 8/36, или 28/36.
Итак, чтобы посчитать все возможные значения, мы умножаем вероятности на их значения, а затем суммируем их, как вот здесь.
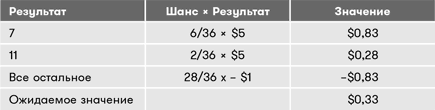
Как видно из таблицы, это хорошая игра, потому что при продолжительной игре вы будете выигрывать в среднем $0,33 за каждый раунд. Но что будет, если только 7 останется выигрышным числом? Это повлияет на ожидаемое значение следующим образом.
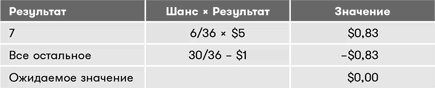
Ноль в графе ожидаемого значения говорит о том, что эта игра похожа на подбрасывание монеты на протяжении долгого времени. Шансы на победу и на поражение абсолютно равны. Давайте теперь вновь изменим правила так, чтобы победной комбинацией было только 11.
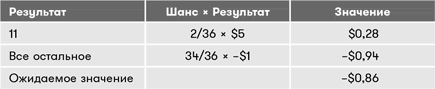
Как вы могли догадаться, в этой игре вы будете обречены на поражение. Вы будете терять в среднем 86 центов за каждый раунд. Конечно, вы можете увеличить свои шансы остаться в плюсе, повысив награду за выпадение 11.
Внимательно взвешивайте значения
Ожидаемое значение – это прекрасный инструмент для настройки игрового баланса, о котором мы поговорим подробнее в следующей главе, но если вы будете не слишком внимательны, рассматривая значения полученных результатов, вы можете пойти по неправильному пути.
Возьмем три типа атаки, которые могут быть частью одной фэнтезийной ролевой игры.

Каким будет ожидаемое значение каждой из этих атак? С ветром все просто – он всегда наносит 4 очка урона, поэтому его ожидаемое значение равно 4. Огненный шар попадает в 80 % случаев и промахивается в 20 %, поэтому его ожидаемое значение (5 × 0,8) + (0 × 0,2) = 4 очка, то есть такое же, как и у ветра. Атака молнией редко достигает цели, но когда все-таки достигает, то разрушает все вокруг. Ее ожидаемое значение – (40 × 0,2) + (0 × 0,8) = 8 очков.
Теперь, исходя из этих значений, можно сделать вывод, что игроки будут всегда использовать атаку молнией, поскольку в среднем она причиняет в два раза больше урона, чем все остальные. И если вам противостоит враг со значением урона 500, такая стратегия себя оправдывает. Но как насчет врагов с уроном 15? Большинство игроков в этом случае не станут использовать молнию, они предпочтут ей что-то слабее, но надежное. Почему так? Ответ таков: несмотря на то что молнией можно нанести 40 очков урона, только 15 из них будут использованы в данной ситуации. Настоящее ожидаемое значение молнии в бою с врагом с 15 очками здоровья – (0,20 × 15) + 0,8 × 0) = 3, что ниже урона, наносимого ветром и огненным шаром.
Вам необходимо иметь четкое представление о реальных значениях для действий в вашей игре. Если что-то дает преимущество, которым игрок не может воспользоваться, или оно подразумевает скрытое наказание, это обязательно нужно учитывать в расчетах.
Человеческий фактор
Также необходимо иметь в виду, что ожидаемые расчеты значений не могут предсказать поведение человека. Вы можете предположить, что игроки будут выбирать преимущественно опцию с самым высоким ожидаемым значением, но так происходит далеко не всегда. В некоторых случаях причина в незнании – игроки просто не знают, что такое ожидаемое значение. Например, не открыв игрокам информацию об относительных шансах ветра, огненного шара и молнии, а предоставив им возможность самостоятельно добывать эту информацию методом проб и ошибок, вы можете заметить, что применившие несколько раз молнию и ни разу не попавшие в цель игроки придут к выводу, что «молния всегда бьет мимо» и поэтому ее ожидаемое значение равняется нулю. Выводы игроков относительно частоты событий как правило бывают ошибочными. Вы должны знать, как игроки воспринимают вероятности в вашей игре, потому что именно они определяют игровой опыт.
Но иногда, даже обладая полной информацией, игроки все равно игнорируют опции с самым высоким ожидаемым значением. Два психолога, Канеман и Тверски, провели интересный эксперимент, в котором спрашивали респондентов о том, в какую игру они хотели бы сыграть.
Игра А
66 % – шанс выиграть $2400
33 % – шанс выиграть $2500
1 % – шанс выиграть $0
Игра Б
100 % – шанс выиграть $2400
Обе игры отличные. Но одинаково ли они хороши? Если сделать расчеты ожидаемого значения…
Ожидаемое значение игры А:0,66 × $2400 + 0,33 × $2500 + 0,01 × 0 = $2409Ожидаемое значение игры Б:1,00 × 2400 = $2400
Как видите, ожидаемое значение игры А чуть выше, чем у игры Б. Но только 18 % участников опроса выбрали этот вариант, тогда как остальные 82 % отдали свое предпочтение игре Б.
Почему? Причина кроется в том, что в расчетах ожидаемого значения нельзя учесть важный человеческий фактор: сожаление. Люди не только склоняются к вариантам, которые доставляют им больше всего удовольствия, но и пытаются избегать тех, которые подразумевают большую вероятность разочарования. Если вы играли в игру А (при условии, что вы играли в нее только раз) и получили $0, вас это сильно расстроит. Люди часто готовы заплатить за то, чтобы уменьшить вероятность разочарования, – «покупают больше мозгов», как говорят продавцы страховых полисов. Несмотря на то что они готовы платить, чтобы избежать разочарования, они еще и готовы рисковать. Поэтому игрок, проигравший немного денег, нередко берет на себя еще больший риск в попытке отыграть деньги обратно. Тверски описал это таким образом: «Когда дело касается заработка, все люди – консерваторы. Вероятному заработку они предпочтут заработок наверняка. Но мы также обнаружили, что, когда люди выбирают между гарантированной потерей и относительно небольшим шансом проиграть по-крупному, они более склонны к риску». Это человеческое свойство сыграло не последнюю роль в успехе условно бесплатной игры Puzzle & Dragons. По мере продвижения через подземелья игроки решают серии головоломок и собирают сокровища. Иногда, правда, они могут погибнуть в подземелье и получить сообщение от игры «Так жаль, что вы погибли. Посмотрите, сколько сокровищ вы сейчас потеряете. Как насчет заплатить немного реальных денег, чтобы сохранить все эти сокровища?» И многие платят, чтобы избежать гарантированной потери своих сокровищ.
Порой человеческий мозг излишне сильно раздувает вероятность некоторых рисков. В одном исследовании Тверски попросил людей оценить вероятность различных причин смерти и получил следующие результаты.
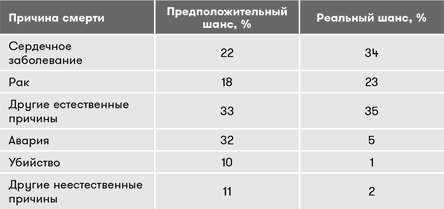
Любопытно, что респонденты в своих оценках недооценили три верхние категории (естественные причины смерти) и значительно переоценили нижние три (неестественные причины смерти). Это искажение реальности можно считать отражением личных страхов респондентов. Но как это можно использовать в геймдизайне? Как дизайнер вы должны иметь контроль не только над реальными вероятностями событий в вашей игре, но и над воспринимаемыми вероятностями, которые не всегда будут соответствовать вашим ожиданиям.
При расчете ожидаемого значения вам нужно будет принять во внимание как настоящие, так и воспринимаемые вероятности, поэтому обратите внимание на призму 35.
Призма 35: Призма ожидаемого значенияЧтобы воспользоваться этой призмой, подумайте о том, каков шанс возникновения тех или иных событий в вашей игре и что они будут значить для игрока. Спросите себя:• Какой шанс возникновения конкретного события?• Какой воспринимаемый шанс?• Какое значение имеет результат события? Можно ли определить это значение? Есть ли у этого значения скрытые аспекты, которые я не учитываю?• Каждое действие, которое игрок может совершить, имеет разное ожидаемое значение, когда я суммирую возможные результаты. Нравятся ли мне эти значения? Они ставят игрока перед интересным выбором? Не несут ли они за собой слишком большое вознаграждение или чрезмерно строгое наказание?Ожидаемое значение – это один из самых важных инструментов геймдизайнера, когда дело касается анализа игрового баланса. Сложность использования этого приема состоит в нахождении способа выразить в виде цифр все, что может произойти с игроком. Получение и потерю денег выразить легко. Но каким будет числовое выражение «ускорения», позволяющего бежать быстрее, или «портала», дающего возможность пропустить два уровня? Эти аспекты трудно измерить, но это не значит, что вы не должны пробовать. В следующей главе мы поговорим о том, что во время тестирования вашей игры и корректировки ее параметров вы измените и собственные оценки значимости различных исходов. Определив количество этих менее заметных элементов, вы сможете понять, что именно имеет большое значение для игрока и почему, – и это понимание позволит вам самостоятельно контролировать баланс вашей игры.
Навыки и шанс объединяются
Какими бы сложными вам ни казались вероятность и разница между настоящими и воспринимаемыми значениями, игровая механика может озадачить вас еще больше. Мы с вами привыкли полагать, что шанс и навыки – это две отдельные механики, но на самом деле их объединяют важные взаимодействия, которые мы не можем игнорировать. Вот список из пяти самых важных взаимодействий между шансом и навыками, которые должен знать каждый геймдизайнер.
1. Оценка шанса – это навык. Во многих играх игрок с высоким навыком отличается от игрока с низким тем, что способен предугадать события в игре, часто благодаря вычислению вероятности. Например, блек-джек – это игра, построенная на знании о вероятности. Некоторые игроки даже ведут подсчет карт, отслеживая, какие карты уже были сыграны, поскольку каждая сыгранная карта изменяет вероятность выпадения последующих карт. Воспринимаемая вероятность в вашей игре может варьироваться в зависимости от уровня навыков игрока.
2. Навыки имеют вероятность успеха. Некоторые люди наивно полагают, что в играх типа шахмат или бейсбола, основывающихся исключительно на навыках, нет места случайностям и риску. Но, с точки зрения игрока, подобные заявления не имеют смысла. Каждому действию присущ некий уровень риска, а игроки постоянно принимают решения по поводу ожидаемого значения, решая, когда нужно играть осторожно, а когда – с долей риска. Иногда эти риски тяжело определить (какова вероятность того, что я смогу забрать ферзя оппонента, чтобы он не заметил?), но тем не менее это тоже риск. При создании своей игры вам необходимо убедиться в сбалансированности этих «чистых случайностей».
3. Оценка навыков оппонента – это навык. Способность игрока определять свои шансы на успех – это также способность оценивать навыки оппонента. Увлекательность многих игр состоит в том, чтобы убедить соперника, что уровень ваших навыков выше, чем он есть на самом деле. Если это удается, противник теряет уверенность в собственных силах. Но существует и обратная стратегия: в некоторых играх убеждение соперника в том, что ваш уровень ниже, чем он есть на самом деле, может привести к потере бдительности со стороны противника, и тот, возможно, будет предпринимать чрезмерно рискованные действия.
4. Предсказание чистой случайности – это воображаемый навык. Люди, как на сознательном, так и на подсознательном уровне, постоянно пытаются вывести закономерности, помогающие им предсказать или предугадать что-либо. Из-за нашей любви к закономерностям мы часто ищем и находим закономерности, которых на самом деле не существует. Два самых распространенных примера «фальшивых закономерностей» – «псевдоудачная полоса» (luckystreak fallacy) (Я выиграл несколько раз подряд, и поэтому я, скорее всего, выиграю еще раз) и «азартное заблуждение» (gambler’s fallacy) (Я проиграл несколько раз подряд, поэтому теперь я должен выиграть). Можно легко посмеяться на этим, но для игрока определение этих «фальшивых закономерностей» является самым настоящим навыком, поэтому вы как дизайнер должны найти способы использовать его в своих целях.
5. Контроль над чистой случайностью – это воображаемый навык. Наш мозг, конечно, пытается во всем находить закономерности, но не менее активно и отчаянно он ищет и причинно-следственные связи. Невозможно контролировать результат, когда мы имеем дело с чистой случайностью, но это не останавливает людей от замысловатых бросков кубика, ношения талисманов и прочих «магических» обрядов. Отчасти именно это мнимое ощущение власти над происходящим делает азартные игры такими интересными. Головой мы понимаем, что это невозможно, но когда ты вот-вот бросишь кубики, шепча про себя «давай, давай…», ты чувствуешь, что контролируешь реальность, особенно если тебе при этом еще и везет! Если, играя в построенную на чистой случайности игру, вы откажетесь от идеи, что ваши действия и мысли могут влиять на результат, большая часть фана этой игры просто пропадет. Наше естественное стремление контролировать судьбу может превращать азартные игры, где все случайно, в игры, где, как нам кажется, мы сами можем все контролировать благодаря нашим навыкам.
Шанс – это сложное хитросплетение математики, человеческой психологии и всех основных игровых механик. Но благодаря этим связям многие игры получают необходимую сложность и глубину. Последняя из списка игровых механик открывает нам призму 36.
Призма 36: Призма шансаЧтобы воспользоваться этой призмой, сосредоточьтесь на тех частях вашей игры, в которых присутствуют случайность и риск, не забывая о том, что это два отдельных понятия. Спросите себя:• Что в моей игре на самом деле случайно? Что кажется случайным?• Случайность дает игроку положительные чувства волнения или отрицательные чувства недостатка контроля?• Моя игра станет лучше от изменения кривой распределения вероятности?• Оставляет ли моя игра возможности для интересного риска?• Как шанс и навыки взаимодействуют в моей игре? Могу ли я как-то добавить к случайным элементам долю демонстрации навыков? Могу ли я увеличить долю риска при демонстрации навыков?Риск и случайность – это как приправы. Игра, в которой эти элементы отсутствуют напрочь, может показаться безвкусной, но, если с ними переборщить, они убьют вкус всего остального. Добавив их в меру, вы только подчеркнете вкус всех остальных составляющих вашей игры. К сожалению, добавить их в игру не так просто, как добавить в суп щепотку соли. Чтобы использовать их в своих целях, вы должны заглянуть внутрь игры и увидеть, где возникают элементы риска и случайности. Но не попадите в ловушку собственных заблуждений, полагая, что элементы вероятности присущи только игральным костям или генератору случайных чисел. На самом деле, эти элементы встречаются везде, где игрок сталкивается с чем-то неизвестным.
Наконец-то мы с вами дошли до конца обсуждения шести основных игровых механик. Вскоре нам придется разобраться с более сложными механиками, такими как головоломки и структуры интерактивных историй, формирующимися на основе шести основных механик. Но сначала нам предстоит научиться тому, как создавать баланс между игровыми механиками.
Назад: Механика 6. Навык
Дальше: Дополнительное чтение

