Книга: Гиппократ не рад. Путеводитель в мире медицинских исследований
Назад: Медицинская статистика
Дальше: Это страшное слово «эпидемиология»
Статистические критерии и заветный p-value
Перед тем как проводить какое-то исследование, нужно чётко определить его цель. Именно она задаёт тон всей остальной работе, ведь, исходя из неё, исследователь сможет представить достижение цели в виде шагов. Эти шаги называются задачами. Допустим, вы хотите исследовать распространённость гриппа типа А среди школьников начальных классов школы № 1. Для этого нужно собрать все школьников, взять у них биологические образцы на анализы, провести эти анализы, а дальше уже сделать какие-то выводы. Всё это – последовательность шагов. Исходя из этой последовательности шагов и того, какие результаты мы хотим получить, выбираются соответствующие статистические методы обработки данных. Все школьники вместе образуют выборку, то есть это люди, которые были выбраны для проведения нашего эксперимента, наблюдения, опроса. Например, в этом случае нам будет вполне достаточно данных о том, сколько всего учеников учится в начальных классах и сколько из них заражены гриппом А.
Ситуация немного усложняется, если мы хотим проверить: кто же болеет гриппом чаще? Мальчики или девочки? Второклассники или третьеклассники? То есть теперь нам нужно ещё и сравнить результаты между группами испытуемых. Для того, чтобы тому, кто потом будет читать наш отчёт, было понятно, по какому признаку мы разделяли учеников, мы должны как-то охарактеризовать всю выборку школьников. Нужно будет указать информацию о том, сколько девочек, сколько мальчиков, сколько учеников какого класса вошло в итоговый статистический анализ. Тут важно помнить, что изначально мы принимаем, что никаких различий между группами не существует. Такое утверждение иначе называется нулевой гипотезой, Н0. В зависимости от цели исследования мы можем пытаться или доказать нулевую гипотезу, или опровергнуть её. Если окажется, что разница в заболеваемости гриппом между мальчиками и девочками всё же существует, мы напишем в отчёте, что нулевая гипотеза была отвергнута. Если же разницы в результатах не будет наблюдаться, мы напишем, что нулевая гипотеза была принята.
Но и это ещё не всё. Согласитесь, будет странно делать выводы о различиях в распространённости гриппа А в разных группах, если в одну группу входит только один человек, а в другую – двадцать. То есть наши группы должны быть каким-то образом сопоставимы. В них необязательно должно быть одинаковое количество человек. Допустимая разница в группах рассчитывается отдельно. Но если в одну группу войдёт 25 человек, а в другую – 26, мы всё равно сможем обработать такую информацию.
Сколько же человек должно вообще нужно исследовать для того, чтобы наши выводы стали корректными и могли применяться повсеместно? По данным сайта Statdata на 1 января 2017 года в России проживает около 8.5 млн детей в возрасте от 5 до 9 лет. Можно ли будет распространить наши результаты на все эти 8.5 млн детей? Нет, ведь наша выборка неидеальна. Мы выбрали только учеников из одной школы. Ситуация улучшится, если мы выберем для анализа данные об учениках из школы № 2? Совсем немного, ведь мы всё ещё находимся в одном городе. Мы хотим получить результаты, которые можно будет распространить на всю страну целиком, значит, нам надо подключить и другие города к нашему анализу.
То, что мы сейчас с вами проговорили, – это мысленная часть эксперимента, всего лишь подготовка к нему. Несмотря на то, что наше исследование казалось совсем простым, в итоге оказалось, что и в этом случае надо аккуратно подходить к делу. Анализ объёма выборки, который необходим для получения результатов исследования, – это крайне важный этап планирования эксперимента. Без проведения вычислений на этапе планирования исследователь может получить слишком маленький объём данных на выходе. В результате наше исследование будет ненадёжным. Если же исследователь, напротив, проводит исследование на очень большой выборке, то он рискует получить слишком много данных. Избыточность данных для статистического анализа не беда, но вот потраченное время и ресурсы могут быть очень ценными. Если речь идёт о клинических испытаниях, то здесь к вопросу о высчитывании необходимой выборки подходят со всем тщанием (конечно, если речь идёт о добросовестных исследователях).
Кроме того, планирование эксперимента позволяет исследователю определить, какова вероятность того, что выбранные им статистические методы будут обнаруживать различия? Насколько велика вероятность ошибки? К сожалению, полностью избавиться от ошибок не удаётся. Как известно, всегда существует вероятность того, что что-то пошло не так. В нашем случае с исследованием распространённости гриппа А добавляется ещё один элемент ошибки. Действительно ли мы можем распространить наши результаты на всех учеников начальных классов в стране? Экономически провести интересующие нас анализы у 8.5 млн детей совершенно невыгодно. То есть мы изначально принимаем, что какая-то вероятность ошибки наших суждений всё же будет существовать. С этим, к сожалению, надо смириться. Но вот второй вопрос более важен: какова величина той ошибки, с которой мы готовы смириться? Пусть мы получили данные о том, что третьеклассники болеют чаще, чем второклассники. Готовы ли мы смириться с тем, что мы ошибаемся в некоторых случаях?
Если вы начнёте читать какие-то биомедицинские исследования, вы практически в любой статье наткнётесь на такой параметр, как p. В английской литературе он называется p-value, в русской – уровень значимости, p-критерий, p-значение. Суть его заключается в том, что он показывает вероятность того, что мы ошиблись. Говоря совсем точно и сухими определениями: это вероятность того, что нулевая гипотеза верна, а мы её отвергли, получив данные, которые мы сочли отличающимися.
В зависимости от типа исследования выбирается определённое значение p. Например, в биоинформатических исследованиях работают с большими объёмами данных. Если выборка составляет 10 000 000, то 1 % ошибки будет для нас слишком велик, ведь 1 % от 10 000 000 равен 100 000. Именно столько раз мы ошибёмся. Поэтому в биоинформатике, как правило, значение p устанавливается совсем маленьким. Если в сравнении в каких-то статистических тестах программа ругается и говорит, что значение p больше установленного числа, означает, что нулевая гипотеза принимается, то есть отличий нет.
В биомедицинских исследованиях критическое значение р, как правило, равно 0.01 или 0.05, что означает 1 % и 5 % ошибок соответственно. Если при сравнении мы обнаружим, что p больше или равно установленному нами порогу, мы смело принимают нулевую гипотезу. На самом деле многими исследователями сейчас критикуется такой подход к оценке полученных результатов. Это связано с тем, что иногда самое по себе значение меньше 0.01 или 0.05 может ни о чём не говорить. Грубое принятие альтернативной гипотезы без каких-то других подтверждающих данных в клинических исследованиях подвергается критике. То есть необходимо учитывать «контекст», а именно остальные данные об исследовании: выборка, используемые методы, качество данных, обоснованность гипотез и выводов. Таким образом, посмотреть в результаты, увидеть заветное «p<0.01», далеко не всегда достаточно для того, чтобы делать выводы о результатах исследования. Более того, в некоторых случаях на одинаковых выборках разные статистические тесты могут давать разные данные, поэтому обычно часть статьи посвящают описанию статистической обработки данных.
О статистических тестах и о том, какие они бывают, мы поговорим немного позднее, а сейчас давайте вспомним, что нам ещё надо для того, чтобы охарактеризовать нашу выборку детей? Допустим, мы всё же заморочились и напрягли коллег из других городов. Коллеги собрали данные, прислали их нам. Теперь мы хотим понять, какая же у нас получилась выборка. Для этого её надо описать: распределение по полу, возрасту, классу, месту проживания, возможно, мы захотим узнать какого роста дети, что они едят, какие секции дополнительно посещают. Для этого нам надо будет вычислять процентные соотношения, средние значения, возможно, строить специальные графики и определять, что же у нас получились за наборы данных. Всё это – описательные статистики. С их помощью мы можем легко донести до читателя все данные о выборке.
После того, как мы всё это проделали, необходимо понять, какой статистический тест надо применять в нашем случае. Для этого надо провести так называемую проверку на нормальность. Суть тут вовсе не в том, что выборка у нас хорошая или плохая, нормальность в статистике обозначает кое-что другое.
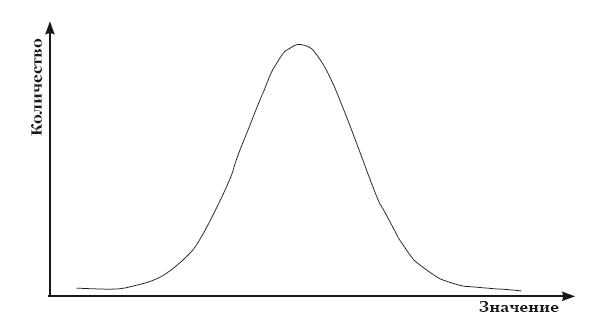
Наверняка вам знакома изображённая выше кривая. По вертикальной оси в нашем случае отложена вероятность какого-то исхода, а по горизонтальной – значение или количество наблюдений, которым соответствует данная вероятность. Кривая такого вида представляет из себя изображение распределения Гаусса, или нормального распределения. Она задаётся определённой функцией, которая нам для рутинной работы не особо важна (хотя как исследователям нам не следует про неё забывать).
Зачем же нам эта кривая? После того, как мы получили результаты, мы оперируем какими-то наборами данных. Мы не можем сравнивать между собой рост и массу тела, потому что это разные категории данных. Но мы хотим сравнить, отличаются ли группы школьников по интересующим нас параметрам, поэтому все эти данные мы должны проверить на нормальность.
Возьмём небольшую выборку из десяти школьников, у которых следующие значения массы тела:
42, 43, 43, 42, 45, 46, 40, 41, 41, 42.
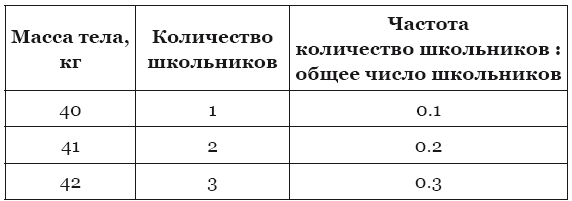
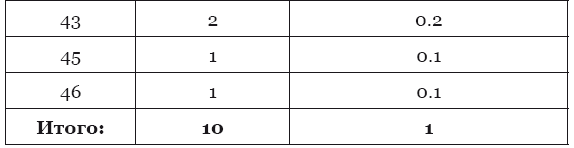
Теперь мы можем построить график по нашей таблице. По горизонтальной оси отложим массу тела, а по вертикальной – частоту встречаемости той или иной массы тела.
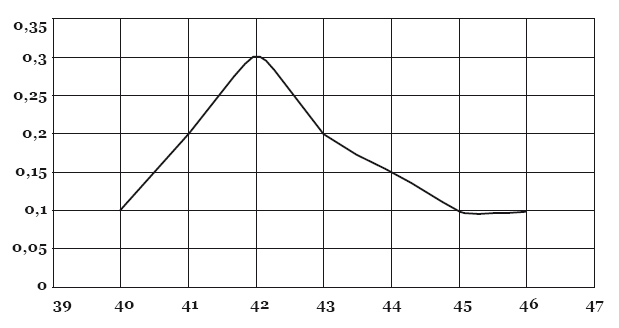
С помощью определённых статистических тестов (как правило, никто, кроме студентов, не делает это вручную, все считают на компьютере) можно определить, насколько получившаяся картина близка к виду нормального распределения. Чем больше точек поставлено на график, тем он, соответственно, будет точнее.
Если результат статистического теста говорит о том, что распределение близко к нормальному, мы должны применять группу статистических тестов, названных параметрическими. Если же распределение отличается от нормального, следует применять непараметрические методы.
Параметрические методы
Что же это за параметры, на которых будет базироваться обработка наших данных? Нашу выборку мы можем описать определённым образом, используя для этого ряд характеристик. Самое простое, что проходят даже в школе, – это среднее. Из нашей выборки 42, 43, 43, 42, 45, 46, 40, 41, 41, 42 мы можем легко найти среднее, просто сложив все числа и поделив их на количество элементов в выборке: 42+43+43+42+45+46+40+41+41+42 = 425, 425: 10 = 42.5. Чуть сложнее находится среднеквардратическое отклонение и ряд других параметров. Параметрические методы названы параметрическими, так как они основываются на оценке полученного распределения.
Однако иногда среднее может нам ничего не сказать. Самая простая ситуация – средняя температура по больнице. Если выборка будет достаточно большой, то средняя температура в любом отделении больницы может оказаться в норме, но это вовсе не будет говорить о том, что пациенты здоровы. Однако температура человека находится в строго определённых пределах и, безусловно, будет подчиняться закону нормального распределения. Что же мы тогда сможем узнать, найдя среднюю температуру в больнице? Мы только опишем наше распределение: температура человека, как правило, будет близка к 37 °C.
Среднеквадратическое отклонение (СКО) в статистике показывает, насколько широк разброс в нашей выборке. Например, для нашей выборки оно будет равно примерно 1.75. Как правило, СКО записывается через знак ±. Тогда мы получаем, что нашу выборку можно описать как минимум так: 42.50±1.75. Это означает, что большая часть элементов выборки находится в пределах от 42.50-1.75 = 40.75 до 42.50+1.75=44.25. В данном случае мы записываем именно 42.50, а не 42.5, так как этого требуют правила математической записи: в СКО у нас получилось 2 знака после запятой.
Среднее и СКО не всегда хорошо описывают выборку, об этом надо помнить. Если распределение асимметрично, данные будут искажены. Для описания таких выборок есть медиана. Если вновь провести аналогию с геометрией, как мы делали ранее для доказательств, то медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис. 6).
Рис. 6. В треугольнике ABC отрезок AM является медианой, то есть разделяет сторону BC пополам
Аналогичную функцию медиана выполняет в статистике применительно к распределению величин. Медиана в статистике – это такое значение, которое разделяет распределение пополам, то есть половина значений распределения больше медианы, а половина – меньше (рис. 7). Мода – ещё один статистический параметр, обозначающий значение, которое встречается наиболее часто в нашей выборке.
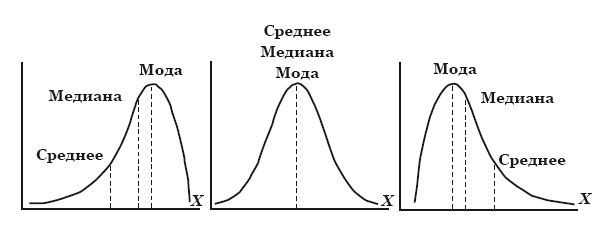
Рис. 7. Среднее, медиана и мода. Слева направо: ассимметричное распределение, нормальное распределение и ассимметричное распределение
Как видно из рис. 7, для идеального нормального распределения среднее и медиана должны совпасть (как и в случае с равнобедренным треугольником), однако если нам нужна информация о том, какое именно значение находится в середине асимметричного распределения, медиана будет гораздо предпочтительнее. Кроме медианы, существуют так называемые процентили, наиболее часто из них используются квартили, то есть 25-й и 75-й процентили. Эти показатели показывают четверть наибольших и наименьших показателей в распределении. Сама медиана считается 50-м процентилем (рис. 8).
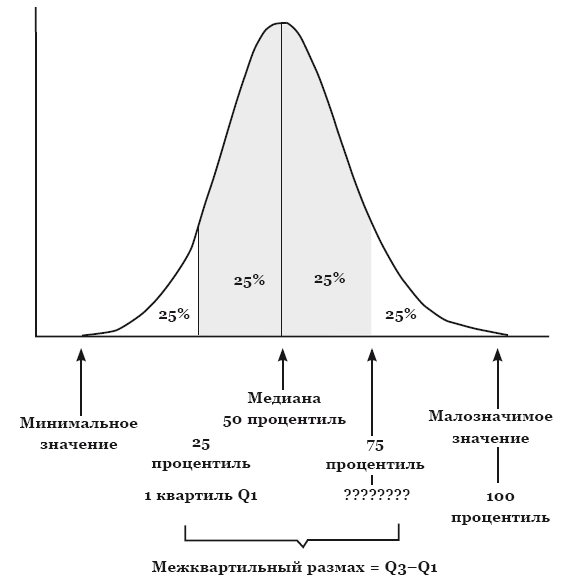
Рис. 8. Распределение с обозначенными минимальным и максимальным значениями, а также медианой и 25-м и 75-м процентилями
Итак, получается, что если наше распределение имеет вид идеальной гауссианы, мы легко можем оперировать параметрами распределения, но если распределение отличается от нормального, нам начинает не хватать среднего и СКО, необходимо вводить другие характеристики, такие как процентили и медиана.
Так как эти статистические характеристики наиболее понятны и просты, параметрические методы в статистике получили большую популярность. Практически ни одно исследование не обходится без их применения. Возраст, масса тела, рост, некоторые биохимические показатели – эти характеристики вполне соответствуют нормальному распределению, а значит, данные можно обрабатывать параметрикой. К параметрическим методам относятся, например, t-критерий Стьюдента, знакомый многим студентам, например по выполнению лабораторных по физике.
Критерий Стьюдента. Самый любимый и самый понятный! По сути он является частным случаем более сложного метода анализа, однако при изучении статистики рациональнее всегда начинать с изучения именно критерия Стьюдента. Данный метод позволяет нам сравнить, насколько отличаются две выборки друг от друга. В англоязычной литературе чаще называется просто t test (подозреваю, что это из-за сходства в написании Student [Стьюдент] и student [студент], что значительно усложняет поиск в Интернете).
Существует два типа t-теста:
• для независимых выборок, когда две сравниваемые группы никак друг от друга не зависят;
• парный (paired) для зависимых выборок, когда две сравниваемые группы зависят друг от друга.
Как правило, критерий применяется в тех случаях, когда испытуемых разделяют на две независимые группы, именно об этом мы и поговорим. Например, пациентов могут разделить на две группы: контрольную, которой дают плацебо, и ту, на которой испытывают реальные лекарства (экспериментальная группа). Таким образом, мы можем получить сразу много данных о каждой группе: какими были интересующие нас показатели (например уровень глюкозы в плазме крови) в группе плацебо до «лечения» и после? А в экспериментальной? Можно сравнить результаты исследований до начала активной фазы исследований и после. Тогда мы поймём, влияет ли как-то наше вмешательство на исследуемые параметры или нет.
Например, наше лекарство должно снижать уровень глюкозы в плазме крови. Если мы честные исследователи, то пациентов в каждую из групп, контрольную и экспериментальную, мы выбирали одинаково по тем же самым параметрам. Значит, и различий между группами по показателю содержания глюкозы в плазме крови до приёма плацебо и лекарства соответственно быть не должно. Но если наше лекарство действует лучше, чем ничего (пустышка-плацебо), значит, после лечения уровень глюкозы должен будет отличаться между группами. Так как глюкоза у нас в организме содержится в строго определённых пределах (меньше и больше определённых значений, к сожалению, означает смерть), а в норме натощак встречается в пределах примерно от 3.5 до 5.5 ммоль/л, можно заранее предположить нормальное распределение. Конечно, наше предположение никак не освобождает нас от необходимости проверки на нормальность: вдруг мы какие-то аномалии получили? Но если нормальность распределения подтверждается, можно использовать t-критерий Стьюдента.
Парный t-тест используется в тех случаях, когда исследователь не разделяет испытуемых на две группы. Они все изначально принадлежат сначала одной группе и проходят через одни и те же процедуры. Исследователь документирует все изменения, которые происходили до и после этих процедур с пациентами. После того, как все эффекты пропадают, пациентов начинают лечить по второй схеме. Все изменения фиксируются и на этом этапе. Парный критерий Стьюдента используется для перекрёстного сравнения таких двух подходов на одних и тех же пациентов, при этом оцениваются одни и те же величины.
Благодаря своей простоте и возможности применения даже на смартфоне при помощи калькулятора этот метод является одним из самых популярных в научной среде. Более того, повсеместность использования t-критерия позволяет вам как исследователю не только сравнивать что-то там у себя в больнице, но и обмениваться данными с коллегами по всему миру. Ведь если вы используете одни и те же методы для обработки данных, которые были собраны одинаково, вы имеете полное право сравнивать их между собой (а потом хвастаться, что у ваших пациентов, мол, показатели куда лучше, чем в соседней поликлинике). Однако не следует забывать, что верные данные и представления о результатах проведённого исследования можно получить тогда и только тогда, когда была правильно проведена вся подготовительная работа.
Для тех, кто захочет самостоятельно что-то вычислить, рекомендую начать с обыкновенных вычислений в Microsoft Excel. Все необходимые формулы легко можно найти в Гугле, только не забудьте заранее найти критические значения t по таблице. Для этого вам необходимо будет выбрать уровень значимости α и знать размер выборки. Этот случай – один из тех, когда первым ссылкам в поиске можно с лёгкостью доверять (рис. 9).
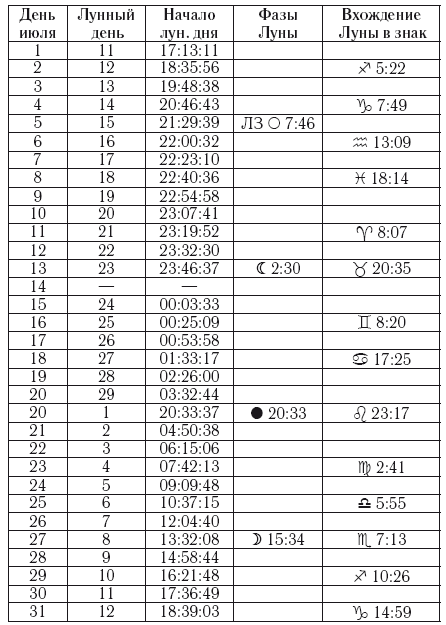
Рис. 9. Фрагмент таблицы со значениями t-критерия для разных уровней значимости и размеров выборки (n)
Множественные сравнения. Наверное, это самая больная мозоль многих исследований, к сожалению, чаще отечественных. Очень часто критерий Стьюдента неверно используется для того, чтобы оценить различия в большем числе групп. Напоминаю, что с помощью t-теста мы можем сравнить только две группы. Некоторые неопытные исследователи (ну или недобросовестные, чего уж греха таить) начинают сравнивать группы попарно. Например, всего было 3 группы, значит, можно сравнить 1 с 2, 2 с 3 и 1 с 3, после чего радостно публиковаться в не самом лучшем журнале (потому что в хороший не возьмут). Если в каких-то сравнениях такой исследователь получает заветное p < 0.05, он с уверенностью заверяет читателей в отличиях между группами, однако не учитывает факта множественных сравнений. По сути-то мы наши выборки использовали не в одном сравнении, а сразу в трёх! Для одного сравнения мы принимали вероятность ошибки в 5 %, но если количество сравнений увеличивается, на том же уровне значимости необходимое значение p также изменяется. Если прикидывать грубо, то в случае горе-исследователя вероятность ошибиться хотя бы в одном сравнении будет примерно 15 %.
Для избегания таких ошибок нужно применять специальные поправки на множественные сравнения. Их существует большое количество, для каждого конкретного случая лучше выбирать определённые поправки вручную с учётом целей исследования и полученных выборок. Самой грубой и простой является поправка Бонферрони, когда новый уровень значимости вычисляется простым делением начального уровня значимости на количество сравнений. То есть в случае с тремя группами (и тремя сравнениями) при уровне значимости 0.05 мы получим: 0.05: 3 = 0.017. Значит, значение p должно быть меньше, чем 0.017, чтобы отличия между группами считались значимыми, иначе вероятность ошибки слишком велика. Поправка Бонферрони применяется не всегда, так как является простейшей и довольно грубой, она довольно резко отсекает верные ненулевые гипотезы. Считается, что она неплохо работает тогда, когда мы проводим небольшое количество попарных сравнений.
Корреляция. Существует такое понятие как корреляция, по-простому это как один параметр зависит от другого, и зависит ли вообще, если да, то в какой степени. Например, с увеличением роста, как правило, увеличивается масса тела, следовательно, эти две характеристики коррелируют между собой. Коэффициент корреляции Пирсона используют для того, чтобы описывать количественные признаки, которые подчиняются нормальному распределению. Существует также коэффициент корреляции Спирмена, который используют в тех случаях, когда о распределении ничего неизвестно.
Тут только нужно особенно отметить тот факт, что «correlation does not imply causation» – корреляция не подразумевает причинно-следственную связь. Самый, к слову, простой пример может показаться довольно банальным. Некоторые дети, которые совершали жестокие преступления, много смотрели телевизор, очевидно, что телевизионные программы делают детей более жестокими. Но на самом деле всё может быть совсем не так, а может и с точностью до наоборот: возможно, жестоким детям просто нравится смотреть телевизор больше, чем нежестоким.
Ещё один пример – вши[29]. Сейчас мы осознаём, что вши – это опасные существа, разносящие опасные заболевания, но наши предки из средневековой Европы очень удивились бы такому повороту событий. Европейские аристократы наряду с прочими правилами этикета изучали также правильные по этикету способы избавления от вшей. Многие считали, что вши и вовсе оказывают положительное влияние на здоровье человека, так как у больных людей этих паразитов обнаруживали реже. Предполагали, что болезнь приходила тогда, когда человек избавлялся от вшей, но на самом же деле эти членистоногие просто очень чувствительны к температуре. Таким образом, корреляция «больше вшей – здоровее человек» никак не поможет нам установить причинно-следственную связь, а, может, даже и натолкнёт на неправильные выводы о том, что вши полезны для здоровья.
Непараметрические методы
Мы уже примерно поняли, когда нужно использовать параметрические методы. Чем же отличаются от них непараметрические? Например, вам нужно исследовать какой-то признак, который нельзя описать числами, какой-нибудь цвет или признак, который подразумевает дихотомичный ответ «да-нет». Подробнее мы остановимся на критерии Манна-Уитни и его многомерном расширении – критерии Краскела-Уоллиса. Интересно в этих методах то, что они являются ранговыми. Это означает, что каждому результату присваивается определённый «ранг». В итоге мы можем сказать о любых двух значениях только то, что одно из них больше или меньше другого, возможно, эти значения равны. Но мы никогда и ни при каких условиях не сможем сказать, на сколько именно одно значение больше или меньше другого. По факту мы всё начинаем измерять «в попугаях».
Такое упрощение даёт нам возможность вообще не заморачиваться о том, какое у нас получилось распределение, и просто наслаждаться жизнью. Мы вообще не интересуемся какими-то там средними, дисперсиями и прочей чепухой, нас интересует только то, чтобы всё как-то магически обрабатывалось. Как говорил известный английский писатель Артур Кларк: «Любая достаточно развитая технология неотличима от магии». В случае применения непараметрических методов эта фраза – наше жизненное кредо. Современные технологии позволяют нам не корпеть над вычислениями, а решать все вопросы двумя нажатиями клавиш на клавиатуре. Непараметрика на бумаге требовала бы от нас многих шагов, но мы избавились от этого, ещё и считаем «в попугаях», ну не сказка ли?
Использовать непараметрические методы необходимо довольно часто. Взгляните вновь на рис. 7: два из трёх распределений асимметричны, они далеко от нормального. Иногда такое распределение можно наблюдать даже тогда, когда, казалось бы, по всем предсказаниям и предположениям распределение должно соответствовать гауссиане. Но жизнь всегда вносит свои коррективы, поэтому повторюсь: мы не освобождены от проверки на нормальность.
Самое интересное, что далеко не факт, что непараметрические методы, применённые на нормальных выборках, покажут исследователю какой-то сущий бред. Есть такой термин, чувствительность теста. Определение этого термина интуитивно понятно: то, насколько тот или иной критерий чувствителен к выявлению различий. Забавный факт в том, что непараметрические методы будут также чувствительны и на нормальных выборках, но чувствительность параметрических методов на таких выборках будет больше. Верно и обратное, хотя параметрика показывает себя на ненормальных распределениях куда хуже.
Кто не рискует, тот не пьёт лекарства
Очень часто в медицинских исследованиях можно увидеть такие непонятные аббревиатуры, как OR и RR. После этого обычно идут какие-то непонятные числа, потом какая-то непонятная аббревиатура CI, а потом ещё какие-то числа… Что это такое и что с этим делать, как оно вписывается в наши представления о статистике?
Дело в том, что в медицине очень важно оценивать риски. Врачи делают это регулярно. Да даже если вы возьмёте в руки инструкцию к какому-то препарату, в очень многих случаях вы сможете увидеть фразу: «…если вероятная польза от лечения превышает возможный риск…» Чаще всего эту фразу можно встретить в разделе инструкции, посвящённом применению препарата беременными женщинами. Ведь некоторые лекарства могут быть опасны для плода, как мы с вами знаем на примере талидомида, поэтому существуют специальные категории, которые определяют класс опасности лекарства для плода.
Риск – это тоже своего рода вероятность. Только в данном случае, как правило, подразумевается что-то не очень хорошее, например наступление болезни или её осложнения. Как и любая другая вероятность, риск принимает значения от нуля до единицы. Под нулём понимают такой исход, когда условная болезнь ни при каких условиях не наступает. Если же риск равен единице, то болезнь наступает всегда, во всех случаях. В медицинских исследованиях оценка рисков позволяет, например, определять, насколько применение лекарств безопасно в тех или иных случаях.
Относительный риск в русскоязычной литературе обычно сокращается до ОР (но не следует путать с отношением рисков), в англоязычной литературе сокращается как RR (relative risk). Представьте, что в исследовании вы проверяете, как марсианская голубика действует на состояние ваших пациентов. Часть пациентов при этом ест марсианскую голубику, а вторая часть не ест её. В каждой из этих групп пациентов будут случаться какие-то неблагоприятные исходы, например, кто-то руку сломает, у кого-то давление скакать будет. В зависимости от того, связаны эти события с вашим исследованием или нет, вы будете их учитывать или не учитывать в конечном анализе данных. Допустим, в группе пациентов, которые ели голубику, частота неблагоприятных исходов, связанных с исследуемым вами состоянием, составила 120 пациентов из 200, а в группе пациентов, которые никакой голубики не ели, – 60 пациентов из 200. Построим такую вот табличку:
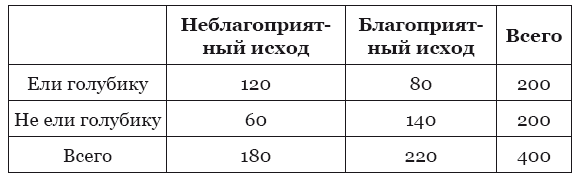
Тогда относительный риск легко найти по такой формуле:

После того, как мы нашли значение относительного риска, нужно ещё найти границы так называемого 95 % доверительного интервала (в русскоязычной литературе сокращается до ДИ, а в англоязычной – до CI от confidence interval). Доверительный интервал на определённом уровне (в нашем случае – 95 %) означает, что с определённой вероятностью (в нашем случае – 95 %) значения исследуемой нами величины (в нашем случае – относительного риска) попадут в посчитанный диапазон. Доверительные интервалы рассчитываются по более сложным формулам, которые имеют отдельный вид для верхней и нижней границы интервала соответственно. Любая программа для обработки данных, однако, посчитает вам доверительный интервал в два счёта, поэтому я не буду приводить эти формулы. В нашем случае верхняя граница получится равной примерно 2.54, а нижняя – примерно 1.57.
Итак, относительный риск получился равен 2. Это позволяет вам сделать вывод о том, что поедание марсианской голубики увеличивает частоту неблагоприятных исходов, грубо говоря, есть эту голубику опасно для здоровья. Так как и нижняя, и верхняя граница доверительного интервала больше единицы, можно сказать, что на уровне значимости p<0.05 наши умозаключения будут статистически верны.
Хорошо, с RR стало понятно, а что же такое OR? Это тоже риск? Нет, OR – это сокращение от odds ratio, или отношение шансов (ОШ). Это тоже статистический показатель, он довольно тесно связан по смыслу с риском, так как также используется для оценки связи между фактором риска и каким-либо исходом. С его помощью можно сравнивать группы пациентов по частотам проявления какого-то интересующегося нас фактора риска. Если грубо, то отношение шансов – это то, насколько присутствие или отсутствие голубики в рационе связано с развитием неблагоприятных исходов в какой-то из групп. В нашем случае отношение шансов можно будет посчитать следующим образом:
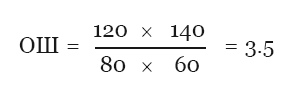
Для оценки статистической значимости также используется доверительный интервал, однако в этом случае он будет вычисляться немного по другим формулам. Значение в 3.5 означает, что наш фактор риска (марсианская голубика в рационе) чаще встречается в группе с наличием неблагоприятного исхода. Если бы значение было меньше единицы, то это говорило бы о наличии обратной связи: голубика бы тогда предотвращала неблагоприятный исход.
Возьмём в качестве примера одну из статей, написанную китайскими исследователями[30], и посвящённую таким прекрасным ферментам, как алкогольдегидрогеназа (алкогольДГ) и альдегиддегидрогеназа (альдегидДГ). Эти ферменты отвечают за переработку этилового спирта и его метаболита ацетальдегида. От их активности зависит то, насколько быстро человек пьянеет и трезвеет, а также то, насколько сильным у него будет с утра похмелье и будет ли оно вообще. Так, если у человека чересчур активен фермент алкогольДГ, то получится, что этиловый спирт будет очень быстро перерабатываться в ацетальдегид. Если при этом альдегидДГ будет плохо работать, то ацетальдегид будет плохо метаболизироваться, что в результате скажется на состоянии человека, и он будет ощущать головную боль и прочие «прелести» алкогольных возлияний.
В принципе, нас не особо сейчас будет интересовать сама методология исследования, наша главная задача – понять, что же китайские учёные написали у себя в аннотации статьи. Итак, исследователи пишут в статье, что есть данные о том, что небольшие изменения в генах этих ферментов могут играть определённую роль в повышении риска ишемической болезни сердца и инфаркта миокарда, но есть также данные, которые опровергают эту информацию. Поэтому китайские учёные решили провести свой собственный анализ всех имеющихся данных на текущий момент и посчитать статистические показатели. В результатах, описанных в аннотации, мы видим такую страшную запись для мутантных генотипов одного из генов, а именно – альдегидДГ:
CAD: RR=1.20, 95%CI: 1.03–1.40, P=0.021;
MI: RR=1.32, 95%CI: 1.11–1.57, P=0.002
CAD – англоязычная версия ишемической болезни сердца (или коронарной недостаточности), а MI – англоязычная версия инфаркта миокарда. Разберёмся, что получили авторы статьи. И для ишемической болезни сердца, и для инфаркта миокарда относительные риски получились больше единицы, 95 % доверительные интервалы также больше единицы, а значение p меньше 0.05. Это означает, что согласно проведённому учёными анализу определённые изменения в гене альдегидДГ связаны с повышенным риском развития этих сердечно-сосудистых заболеваний. А что же с алкогольДГ?
CAD: RR=0.92, 95%CI: 0.73–1.15, P=0.445;
MI: RR=0.93, 95%CI: 0.84–1.03, P=0.148
Исследованные авторами изменения в гене алкогольДГ, согласно этим данным, не связаны с развитием ишемической болезни сердца и инфаркта миокарда.
Назад: Медицинская статистика
Дальше: Это страшное слово «эпидемиология»

