Часы, сделанные человеком, действуют по удивительно простому принципу — считают число циклов осциллятора. Устройство осциллятора может быть самым разным — качающийся маятник, вибрирующий кристалл кварца, циклы «вибрации» электромагнитного излучения, но суть одна: такие часы просто считают циклы периодических процессов. Учитывая невероятную успешность этой стратегии, невольно задумаешься о том, что мозг для определения времени мог бы использовать аналогичный механизм.

Пожалуй, это искушение слишком велико.

Самая популярная теория, объясняющая механизм отсчета времени мозгом в диапазоне от миллисекунд до секунд, называется моделью внутренних часов; впервые эта теория была выдвинута в начале 1960-х гг. Как следует из названия, данная модель предполагает, что часы мозга работают по тому же принципу, что и часы, сделанные человеком: нейроны или группы нейронов пульсируют с какой-то фиксированной частотой, а другая группа нейронов считает эти пульсации. Это кажется вполне реалистичным, тем более что многие нейроны действительно осциллируют — возбуждаются снова и снова через определенные интервалы времени. Вообще говоря, мозговые волны, дыхание, ходьба и сердцебиение — примеры ритмичных биологических процессов, основанных на биологических осцилляциях с периодом от десятков миллисекунд до нескольких секунд.

Но в часах, сделанных руками человека, кроме хорошего осциллятора есть еще механизм, способный подсчитывать осцилляции — шестеренки в механических часах или цифровые схемы в кварцевых часах. Здесь-то и кроется проблема: хотя нейроны могут быть прекрасными осцилляторами, в подсчетах они не сильны.

Возможно, вы сейчас думаете: подождите-ка, мы уже видели, что циркадные ритмы основаны на действии биологического осциллятора, работающего по принципу саморегулирующейся транскрипционно-трансляционной петли обратной связи. Более того, как мы только что отметили, ритм дыхания, сердцебиения или ходьбы тоже основан на действии осцилляторов. Так что для отсчета времени организм действительно использует тот же принцип, что заложен в основу работы механических или кварцевых часов! Однако такая линия рассуждений справедлива лишь отчасти, поскольку существует одно важное различие между вышеуказанными физиологическими процессами и работой часов, изготовленных человеком. В приведенных выше примерах интервалы времени, измеряемые «биологическими часами», меньше или равны периоду осцилляций, тогда как для часов, изготовленных человеком, ситуация обратная: такие часы способны определять время только в диапазоне времени, превышающем период осцилляций. Биологические осцилляторы обычно хронометрируют события, длительность которых меньше периода колебаний, а часы, изготовленные руками человека, работают с отрезками времени, длительность которых превышает период колебаний.

Молекулярный механизм циркадного ритма, обсуждавшийся в главе 3, имеет период около 24 ч. Концентрация белков циркадного ритма, таких как Period, соответствует фазам этого 24- часового цикла (например, утро, день, ночь). Но циркадные часы наших супрахиазматических ядер не имеют ни малейшего представления о том, сколько дней прошло с того или иного момента времени! Каждый день показатели этих «часов» возвращаются к нулевому значению; представьте себе маятник, не связанный ни с каким часовым механизмом: глядя на него, нельзя установить, сколько колебаний он уже совершил.

Аналогичным образом осцилляции нейронов, обеспечивающие дыхание, позволяют дышать с более или менее регулярной частотой, скажем, 0,25 Гц (каждые 4 с). Для каждого цикла вдоха и выдоха необходимо совершить ряд хронометрированных движений. Поэтому можно сказать, что нервные центры, контролирующие дыхание, отсчитывают время в пределах 4 с, но после этого механизм вновь возвращается в исходное положение. Сети нейронов, контролирующие дыхание, не имеют никакого представления о том, совершили ли они тысячу, миллион или миллион и один цикл дыхательных движений.

Сети нейронов интегрируют временную информацию (количество осцилляций), но не обладают точностью и памятью часов с маятником или цифровых сетей кварцевых или атомных часов. После тренировки человек может различить интервалы времени длительностью 100 и 105 мс. Но чтобы обнаружить эту разницу в 5 мс, осциллятор должен работать с частотой 200 Гц, а приемное устройство должно уметь отличать 20 осцилляций от 21, что весьма непросто, учитывая механизм действия нейронов. Вполне в соответствии с этими теоретическими рассуждениями у нас совсем немного экспериментальных данных, которые подтверждали бы справедливость модели внутренних часов.

Однако отсутствие экспериментальных данных в поддержку модели внутренних часов вовсе не означает, что осцилляции нервных клеток мозга не связаны с хронометрированием событий, длящихся дольше периода колебаний. Например, было выдвинуто предположение, что некоторые формы определения времени могут основываться на активности нейронов, осциллирующих с разной частотой. При таком сложном механизме осцилляций разные субпопуляции нейронов с какой-то периодичностью синхронизируются, но в остальное время действуют не в фазе. Расчеты показывают, что путем определения этих синхронных пульсаций модель нейронных осцилляций позволяет дискриминировать интервалы времени меньше периода колебаний любой группы осцилляторов.

Как мы уже обсудили, отсчет времени в диапазоне от сотен миллисекунд до нескольких секунд играет для нас очень важную роль. Речь идет не только о чрезвычайно точном определении интервалов между событиями, но и об оценке контекста, учете временно́й иерархии и восприятии временны́х образов. В этой «зоне обитаемости» мы можем оценивать длительность событий и длительность промежутков между ними, а также отслеживать общую структуру последовательности фонем, музыкальных звуков, точек и тире азбуки Морзе. По этой причине для объяснения принципов отсчета времени в диапазоне от нескольких миллисекунд до нескольких секунд нам следует заглянуть за пределы общепринятой теории осциллирующих нейронов.

Посмотрите на разбегающиеся по воде круги, образованные двумя каплями дождя (рис. 6.1). Какая капля упала первой? Одна из задач данной главы заключается в том, чтобы продемонстрировать, что для определения времени теоретически подходит любое физическое явление, которое можно повторить воспроизводимым образом (об этом нам напоминает цитата из книги Эйнштейна и его коллеги Леопольда Инфельда, использованная в качестве эпиграфа к данной главе).

Если все капли дождя падают на поверхность воды с одинаковым импульсом, все они создают примерно одинаковые серии концентрических кругов. Эти круги — пример пространственно-временно́го рисунка: пространственного образа, изменяющегося во времени. Моментальный снимок этого рисунка в любой момент времени не только показывает, какая капля упала раньше, но и позволяет (с применением несложной математики) рассчитать интервал времени между падением капель.

Рис. 6.1. Круги на воде. По определению динамические системы — это системы, состояние которых зависит от фактора времени. Глядя на эту фотографию, легко определить, какая капля упала первой, и можно оценить интервал времени между падением двух капель.

Давайте рассмотрим еще один простой пример изменяющейся во времени системы, которую теоретически можно использовать для определения времени. Представьте себе ребенка, спускающегося с водяной горки в бассейне: если каждый раз он начинает спускаться с одного и того же места, он достигает дна примерно через один и тот же промежуток времени. Мы можем пометить отрезки, которые ребенок проезжает за одну секунду: вверху эти отрезки будут короче, внизу — длиннее, поскольку скорость движения увеличивается. В результате, по мере того как ребенок пересекает каждую следующую линию, можно определить, сколько времени прошло от момента старта.

Таймер «ребенок на горке» запускается силой тяжести, как водяные или песочные часы. Возможно, такие часы кажутся вам не очень точными, но знайте, что восемь сильнейших спортсменов в соревнованиях по скоростному спуску на лыжах во время Зимней Олимпиады 2014 г. показали результаты с разницей в пределах полсекунды — от 2:06:75 до 2:06:23. Эта точность (погрешность менее 0,4 %) выше точности любых часов, изобретенных до маятника Гюйгенса.

В большинстве физических систем (спускающийся с горы лыжник, скатывающийся с горки мяч, биохимическая реакция в клетке, круги на воде) развитие процессов во времени определяется законами физики, т. е. эти системы теоретически можно использовать для определения времени. Головной мозг — самая сложная на свете динамическая система, так что кажется логичным, что для определения времени мозг использует протекающие в нем самом динамические процессы. Ведь каждый раз, когда нейрон возбуждается, в нем запускается серия воспроизводимых изменений, во многом напоминающих изменения, вызываемые падением дождевой капли в пруд.

В главе 2 мы обсуждали, что нейроны соединены друг с другом через синапсы, и что сила синапса определяет степень влияния пресинаптического нейрона на постсинаптический нейрон. Более того, сила синапсов может меняться (слабый может стать сильным), и это явление синаптической пластичности — один из механизмов, позволяющих мозгу воспринимать и хранить информацию.

Нейробиологи упрощают ситуацию, когда говорят, что в отсутствие обучения сила синапсов остается более или менее постоянной. Большинство синапсов становятся сильнее или слабее при каждом использовании, т. е. после каждого пресинаптического «спайка». Такие зависимые от использования изменения силы синапса называют кратковременной синаптической пластичностью; они длятся во временном диапазоне от десятков миллисекунд до нескольких секунд.

Некоторые синапсы коры головного мозга испытывают кратковременную фасилитацию (облегчение); например, если пресинаптический нейрон последовательно генерирует два «спайка» с интервалом 100 мс, второй «спайк» приводит к более сильному изменению потенциала постсинаптического нейрона, чем первый (рис. 6.2), так что «вес» сообщения, переданного пресинаптическим нейроном постсинаптическому нейрону, увеличивается.

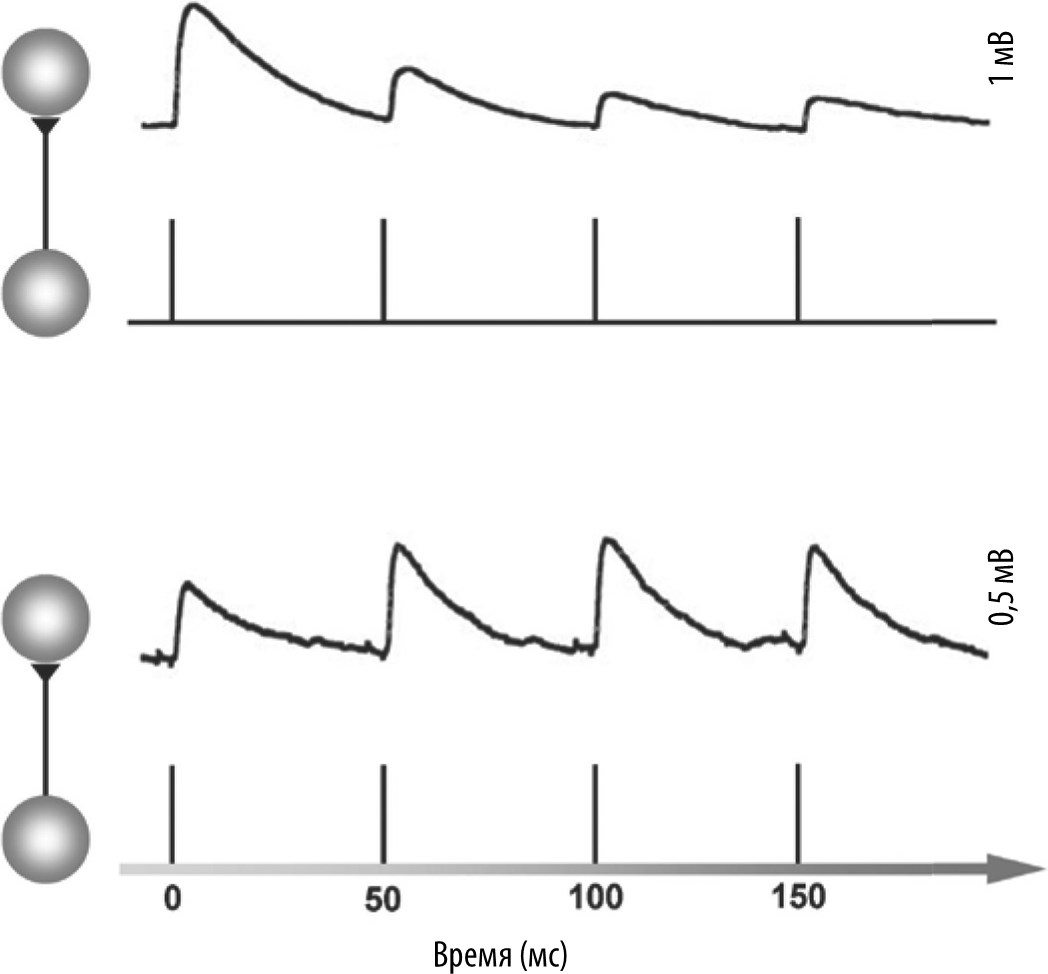
Рис. 6.2. Кратковременная синаптическая пластичность. В диапазоне миллисекунд сила синапса может испытывать кратковременную депрессию (вверху) или кратковременную фасилитацию (внизу); воспроизводится в соответствии со статьей Reyes and Sakmann, 1999.

Однако большинство синапсов коры испытывают кратковременную депрессию: второй «спайк» из пары «спайков», возникших с интервалом 100 мс, вызовет меньшее изменение потенциала в постсинаптическом нейроне.

Но в любом случае степень изменения потенциала зависит от времени между «спайками». Обычно максимальный эффект достигается при промежутке времени меньше 100 мс, и практически исчезает, если «спайки» разделены во времени несколькими сотнями миллисекунд. Следовательно, подобно тому, как диаметр внешнего кольца от капли воды, упавшей на поверхность пруда, содержит информацию о том, как давно упала капля, так сила синапса в любой момент времени содержит информацию о том, как давно этот синапс использовался в последний раз.

Мы предположили, что кратковременная синаптическая пластичность и другие зависящие от времени свойства нейронов могут вносить вклад в способность мозга определять время в диапазоне порядка сотен миллисекунд. Давайте рассмотрим простейшую сеть нейронов: два нейрона, соединенные единственным синапсом (рис. 6.3). Допустим, что пресинаптический нейрон возбуждается в одном из трех возможных режимов, когда два пиковых потенциала («спайка») наблюдаются с интервалом 50, 100 или 200 мс. Эти интервалы можно считать временны́ми стимулами. Например, некоторые животные общаются между собой посредством «щелчков» — коротких серий звуков, интервалы между которыми несут определенную информацию. Во всех трех случаях первый «спайк» вызывает одно и то же изменение потенциала (допустим, 1 мВ). За счет кратковременной синаптической пластичности сила синапса в момент прохождения второго «спайка» будет изменяться. Если второй «спайк» проходит через 50 мс, изменение напряжения может достигать 1,5 мВ, а если он проходит через 100 и 200 мс, напряжение составляет 1,25 и 1,1 мВ соответственно. Допустим, наша сеть действует таким образом, что постсинаптический нейрон возбуждается только в том случае, если получает сигнал не слабее 1,5 мВ, и в таком случае мы имеем своеобразный таймер: нейрон, возбуждающийся при получении двух сигналов с интервалом 50 мс.

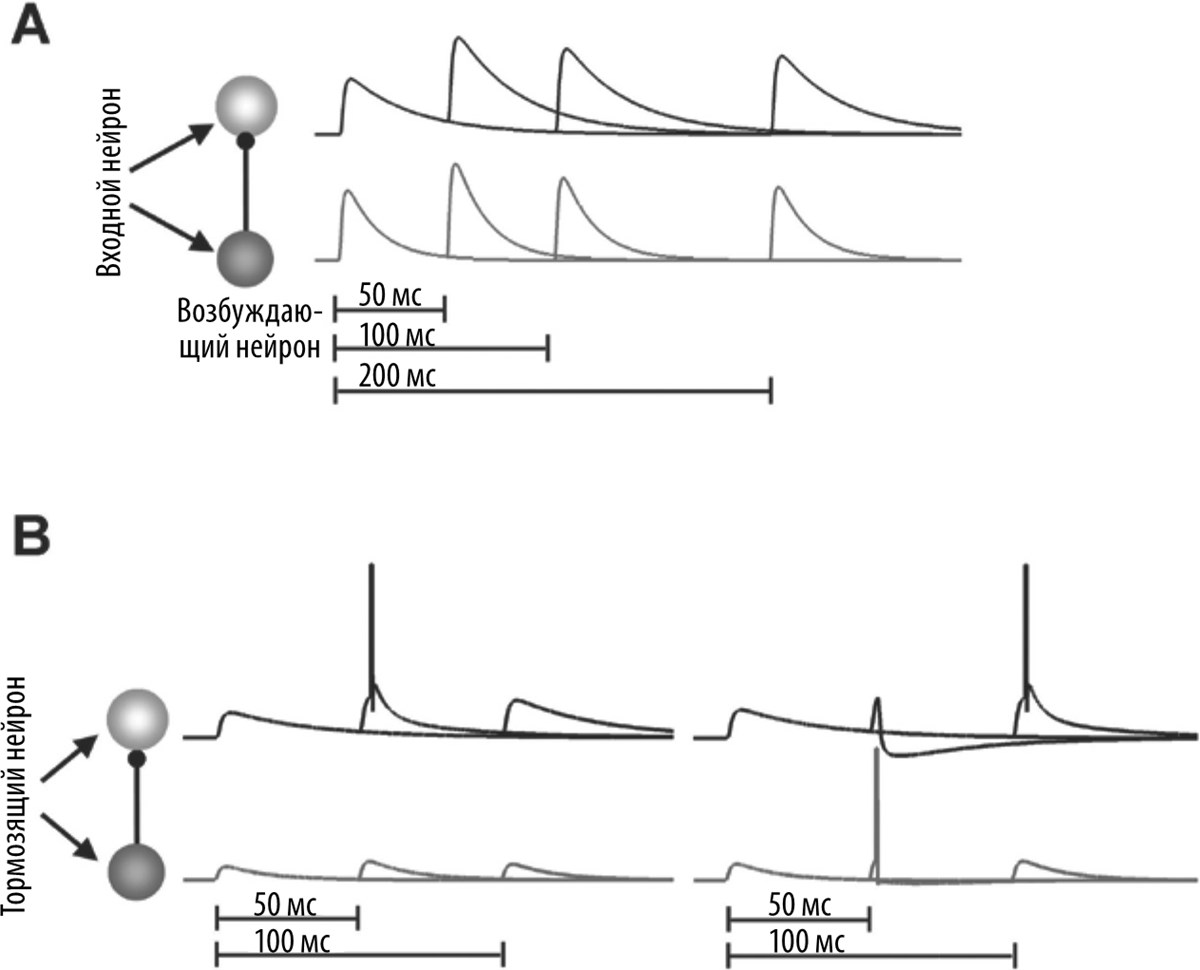
Рис. 6.3. Селекция интервалов, основанная на кратковременной синаптической пластичности

А. В этой простой нейронной сети входной нейрон контактирует с возбуждающим (вверху) и тормозящим (внизу) нейроном. Графики показывают изменения потенциала при трех интервалах времени между пиковыми потенциалами («спайками») входного нейрона — 50, 100 и 200 мс. Синапсы между пресинаптическим и двумя постсинаптическими нейронами испытывают кратковременную фасилитацию: например, амплитуда второго пикового потенциала, возникающего через 50 мс, больше амплитуды первого пикового потенциала.

В. В зависимости от силы синапсов между пресинаптическим и постсинаптическими нейронами возбуждающий постсинаптический нейрон может избирательным образом реагировать на интервал 50 (слева) или 100 (справа) мс. Таким образом, этот возбуждающий нейрон в самой простой сети в некотором смысле может отсчитывать время.

Компьютерные модели нейронных сетей показывают, что простые сети возбуждающих и тормозящих нейронов, демонстрирующих кратковременную синаптическую пластичность, могут избирательным образом реагировать на разные интервалы времени: например, отвечать на интервал длительностью 100 мс, но не 50 или 200 мс. Такие настроенные на определенный интервал нейроны в принципе могут служить для определения времени начала озвончения фонем, интервалов между знаками в азбуке Морзе или между музыкальными нотами.

Исследователи обнаружили такие нейроны, избирательным образом реагирующие на разные интервалы времени, в мозге многих животных — от кур и крыс до электрических рыб. Мы пока не знаем точно, как возникает этот избирательный ответ, но некоторые исследования показывают, что как минимум отчасти это связано с кратковременной синаптической пластичностью.

Понятно, что представленная выше упрощенная схема, состоящая из двух нейронов, чрезвычайно сильно отличается от реальной ситуации в мозге. В кубическом миллиметре ткани коры головного мозга могут содержаться сотни тысяч нейронов и сотни миллионов синапсов. Существуют гораздо более общие модели, объясняющие, каким образом сети нейронов коры мозга обрабатывают сложные пространственные и временны́е образы. В частности, наша лаборатория, а позднее австрийский математик Вольфганг Маасс и его коллеги предложили так называемую модель сети, зависящей от состояния. Чтобы понять суть модели, нужно понять концепцию состояния кортикальной сети.

В физике под состоянием системы понимают набор параметров, дающих существенную информацию о текущей «конфигурации» системы. Представьте себе несколько шаров на бильярдном столе. Состояние такой системы можно описать положением и импульсом (произведением массы на скорость) каждого шара. В принципе, знание состояния шара в какой-то момент времени позволяет предсказать не только, что произойдет в следующий момент, но и что происходило недавно: зная состояние системы в момент времени t, в соответствии с законами физики можно определить ее состояние в моменты времени t-1 и t+1. Каков эквивалентный набор параметров, который мог бы позволить нам определять состояние группы нейронов головного мозга?

Обычно состояние сети нейронов в конкретный момент времени определяется тем, какие нейроны находятся в возбужденном состоянии. Я буду называть это активным состоянием, поскольку по нему можно определить, какие именно нейроны активно передают информацию своим партнерам. Однако это далеко не полное описание состояния сети, поскольку только на основании активного состояния нельзя предсказать, как будет вести себя сеть в следующий момент. На поведение сети в будущем влияют многие другие свойства нейронов. Одно такое свойство — кратковременная синаптическая пластичность. Понятно, что состояние группы нейронов в следующий момент зависит не только от того, какие нейроны возбуждены в настоящий момент, но и от эффективной силы каждого синапса в каждый момент времени, а это, в свою очередь, зависит от того, что эти синапсы делали в прошлом. Кратковременная синаптическая пластичность — лишь одно из многих свойств нейронов, способных изменяться в диапазоне времени порядка сотен миллисекунд. Такие свойства описывают скрытое состояние сети: «скрытое» по той причине, что электроды нейробиологов не могут их проанализировать.

Активное состояние сети в момент времени t определяется входным сигналом и состоянием (активным и скрытым) в момент времени t-1. Можно еще раз воспользоваться аналогией с кругами на воде. Представьте себе, что на поверхность пруда падают две капли дождя: первая в момент времени t = 0, вторая — в момент времени t = 100 мс. Состояние поверхности пруда в момент времени t = 101 мс будет зависеть от взаимодействия между вторым сигналом (второй каплей) и текущим состоянием (волнами, созданными на поверхности пруда первой каплей). Важно, что характер волн от падения второй капли будет разным, если она упадет через 100 и через 200 мс после первой. Вывод таков, что, глядя на моментальный снимок поверхности пруда в момент времени t = 400 мс, мы сможем определить не только, сколько капель упало, но и оценить интервал времени между их падением (если их было две): недавнее прошлое поверхности пруда отражается в его настоящем. Аналогичным образом ответ сети нейронов определяется текущим входным сигналом и состоянием системы в недавнем прошлом, которое каким-то образом закодировано в настоящем. Таким образом, «ответ» поверхности пруда и сети нейронов зависит от состояния. Действительно, мониторинг активности зрительной и слуховой коры показывает, что ответ сети нейронов на стимул сильно зависит от предыдущих стимулов и от времени, которое прошло после их действия. Компьютерное моделирование показывает, что зависящие от состояния сети нейронов могут различать не только интервалы времени, но и сложные пространственно-временны́е образы, такие как разговорная речь.

Говорим ли мы о кругах на воде или об изменении состояния сети нейронов как о механизме определения времени, мы пока не ответили на главный вопрос: как работает этот механизм? Как перевести круги на воде или состояние сети нейронов в единицы времени? Экспериментальные и теоретические исследования позволяют предположить, что один из способов кодирования времени заключается в том, что мозг определяет, какие нейроны активны в каждый конкретный момент времени.

Мы уже рассмотрели простой вариант этой концепции, когда обсуждали активность нейронов в специфическом отделе мозга (HVC) у певчих птиц. Время, прошедшее от начала песни, можно определить по тому, какой конкретно нейрон возбужден в данный момент — подобно тому, как по номеру падающей в данный момент костяшки домино можно узнать, когда упала первая костяшка из стопки. Однако это очень примитивный линейный код. В более общем виде идея заключается в том, что в каждый момент времени активной является большая группа (субпопуляция) нейронов. Я буду называть эту модель моделью популяционных часов.

Впервые эту важную идею выдвинул нейробиолог Майкл Маук, тогда работавший в Университете Техаса в Хьюстоне. В 1990-х гг. Маук предположил, что какие-то формы отсчета времени основаны на активности динамически изменяющихся популяций нейронов мозжечка — анатомически различимой части мозга, участвующей в координации движений. Например, давайте предположим, что в момент t = 0 некий звуковой стимул вызывает возбуждение нейронов мозжечка. Тогда через 100 мс может активироваться субпопуляция нейронов, состоящая из нескольких тысяч клеток, а еще через 100 мс активируется другая субпопуляция. Даже если какие-то нейроны активны в оба момента времени, и ни один нейрон напрямую не сообщает время, такие популяционные часы все равно позволяют понять, сколько времени прошло от момента t = 0: 100 или 200 мс.

В качестве аналогии представьте себе многоэтажный дом со светящимися окнами. Вы смотрите на окна дома и видите, где горит свет, а где нет. Теперь представьте себе, что люди в этом доме живут по странному расписанию. В одном окне свет зажигается на закате, в другом — через час после заката, в третьем свет зажигается на закате, потом выключается через час, а потом вновь зажигается через три часа. Если в доме 100 окон, с помощью двоичной цифровой системы можно записать состояние окон дома в каждый момент времени: 1 0 1 … на закате, 0 1 1 … через час после заката, и т. д. (в данном случае каждая цифра означает, включен свет (1) или выключен (0)).

Распределение включенных и выключенных окон описывает состояние дома в каждый момент времени (эквивалент активного состояния сети нейронов). Это состояние можно изобразить в виде точек на графике, на котором каждая ось соответствует одному окну. Проблема заключается в том, что нам в таком случае понадобится построить график с 100 осями. На рис. 6.4 показано, как бы мы описали состояние здания в разные моменты времени, если бы у нас было всего три измерения, соответствующих осям x, y и z. Хотя мы не можем изобразить такой график в 100-мерном пространстве, принцип был бы точно таким же. Соединяя точки, соответствующие каждому моменту времени, можно воссоздать траекторию здания — изменение состояния окон во времени. И хотя здание совсем не предназначено для того, чтобы служить в качестве часов, благодаря этой внутренней динамике (изменению рисунка освещенности окон) с его помощью можно определять время.

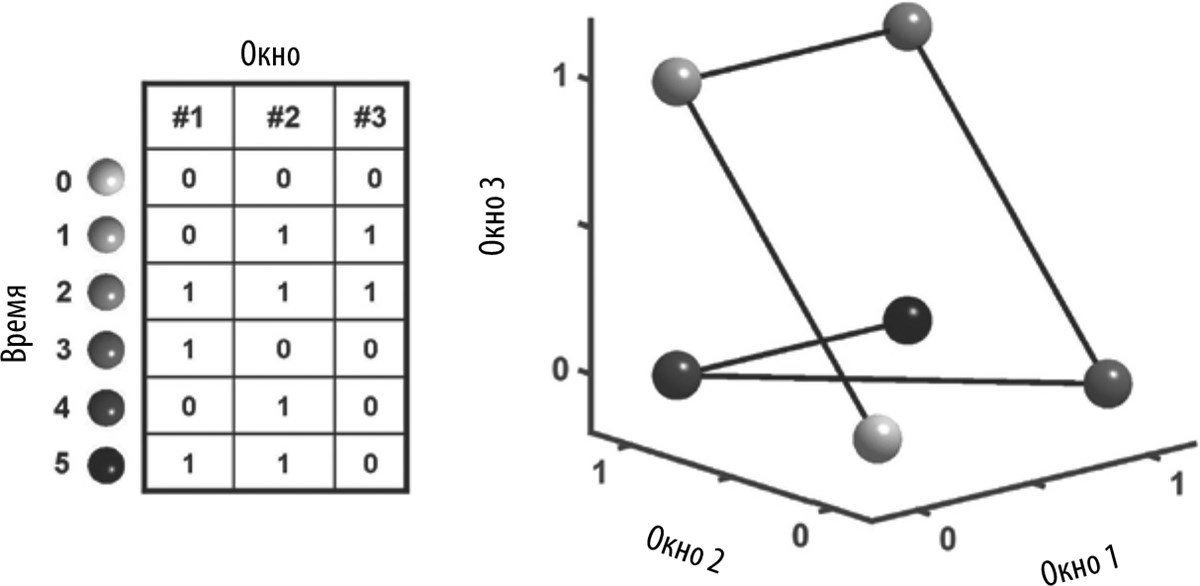
Рис. 6.4. Кодирование времени с помощью изменения освещенности окон здания. Состояние трех окон здания в каждый момент времени (таблица слева) можно представить в виде траектории в трехмерном пространстве (справа).

Теперь мы можем представить себе, каким образом изменение картины активации нейронов теоретически может служить в качестве часов. Однако важнейший вывод, который следует из теории Майкла Маука, заключается в том, что сеть из большого числа нейронов представляет собой не одни часы, а множество. Возможно, нам не сразу понятны преимущества использования одной и той же сети в качестве нескольких разных часов, однако такая стратегия создает основу для более мощного вычислительного аппарата.

Допустим, у вас на кухне есть таймер, который можно запрограммировать на определенное время, необходимое для приготовления яйца всмятку, варки макарон или выпечки пирога. Другая стратегия — купить три таймера, по одному для каждой задачи, и у каждого свой звонок. Да, эти три таймера будут занимать на кухонном столе много места, но у этой системы, специфической для каждого действия, есть важное преимущество: когда вы входите в кухню и слышите звонок, вы сразу знаете, нужно ли что-то снять с плиты или выключить духовку. Другими словами, часы, реагирующие на специфические события, одновременно закладывают в память информацию о текущих событиях.

Чтобы лучше понять преимущество наличия множества часов в одной сети нейронов, давайте представим себе новогоднюю елку с гирляндой из тысячи светодиодных ламп. Допустим, при каждом включении гирлянды лампочки начинают светиться по-другому, чем раньше. Вариантов может быть множество: лампочки могут поочередно мигать или исполнять сложный танец, как окна в гипотетическом многоэтажном доме из нашего предыдущего примера. Преимущество первого режима заключается в том, что его легко расшифровать: первая лампочка включается в момент времени t = 1, вторая — в момент времени t = 2 и т. д. Недостаток таков, что такой режим всего один, так что и таймер всего один. Напротив, сложный режим трудно расшифровать, зато один и тот же набор лампочек можно использовать для создания огромного множества таймеров.

Допустим, наша гирлянда имеет два переключателя: один у Элис, другой у Боба. Представим себе, что переключатель Элис активирует следующий режим включения лампочек с интервалом в 1 с (номера соответствуют положению каждой лампочки в цепи):

А переключатель Боба запускает другую последовательность (заметьте, что в этом случае алгоритмы включения лампочек в разные моменты времени разные):

В таком случае, если вы смотрите на елку и видите, что включены лампочки под номером 8, 16, 24, 32 и т. д., вы знаете не только, что прошло четыре секунды после включения гирлянды, но и что ее включила Элис. Таким образом, наши новогодние лампочки описывают и время, и пространство, поскольку определяют, сколько времени прошло от момента включения, и какой переключатель был активирован. Зачем мозгу часы, действующие по такому принципу? По той причине, что в диапазоне времени от нескольких миллисекунд до нескольких секунд ему нужно не только определять время, но и выполнять определенные действия в определенные моменты времени.

Один известный пример хронометрированного движения у животных представляет собой классический условный рефлекс: если через 250 мс после звукового сигнала на сетчатку глаза направлять струю воздуха, постепенно человек и другие животные обучаются моргать в ответ на звуковой сигнал. Однако они мигают не в тот момент, когда слышат звук, а тогда, когда предчувствуют появление воздушной струи. Другими словами, животные не просто учатся моргать, они учатся, когда именно моргать. Это важный навык, поскольку в ситуации, когда опасное воздействие может повредить сетчатку, держать глаза закрытыми слишком долго — тоже не самый лучший выход.

А могут ли животные научиться моргать в разные моменты времени в ответ на разные звуки? Именно это продемонстрировали эксперименты Майкла Маука. Сотрудники его лаборатории показали, что кролики могут научиться моргать примерно через 150 мс после низкочастотного звукового сигнала и через 750 мс после высокочастотного сигнала. Кроме того, повреждение мозжечка приводило к исчезновению этой способности, так что, вероятно, эти нейронные часы располагаются где-то в мозжечке.

Вот еще один пример, раскрывающий преимущество множества часов. Представьте себе пианиста, умеющего играть на пианино две песни. В первой песне через секунду после начала должна звучать нота до, а в другой — нота ми. Обычные часы подскажут вам, когда пройдет секунда, но они не скажут, какую клавишу нужно нажимать. Однако использование в качестве таймера динамического пространственно-временного режима (как различные режимы переключения гирлянды в примере с Элис и Бобом) поможет решить не только проблему определения времени, но и подскажет, что в какой момент нужно делать. Мозг может использовать эту стратегию, связывая популяцию нейронов, активных на протяжении секунды в первой песне, с двигательными нейронами, отвечающими за нажатие ноты до, а популяцию нейронов, активных на протяжении секунды во второй песне, с двигательными нейронами, ответственными за нажатие ноты ми.

Ученые проанализировали множество примеров простых и сложных картин активности нейронов, которые, возможно, отвечают за определение времени. Нейробиолог Джо Пейтон из Центра изучения неизвестного (фонд Шампалимо) в Лиссабоне натренировал крыс тыкаться носом в одну из двух «дверей» в зависимости от длительности временного интервала между звуками. Крысы слышали два звука, разделенные интервалом времени от 0,6 до 2,4 с. Если они тыкались носом в левую дверь после интервала короче 1,5 с и в правую дверь после интервала длиннее 1,5 с, они получали вознаграждение. Крысы довольно хорошо справлялись с заданием. Например, временны́е интервалы длительностью 1 и 2 с они распознавали с вероятностью около 90 %.

Пока крысы занимались этим важным делом, исследователи анализировали состояние нейронов полосатого тела их мозга — отдела головного мозга, задействованного в выполнении движений и в некоторых формах обучения. Многие нейроны этого отдела мозга возбуждались во время упражнения. Например, в эксперименте с интервалом времени длительностью 2,4 с некоторые нейроны возбуждались рано, другие позже, так что возникала своеобразная цепочка возбуждения A→B→C→D→E (эта схема сильно упрощает реальную ситуацию). В экспериментах с интервалом времени вблизи пограничного значения 1,5 с крысы, как и ожидалось, совершали больше ошибок. Интересно, что по динамике поведения нейронов эти ошибки можно было предсказать. Например, когда цепочка активности развивалась «слишком быстро», крысы с большей вероятностью решали, что интервал был длинным, и наоборот.

В целом данные эксперименты показывают, что нейроны этой области мозга задействованы в определении времени, хотя, как чаще всего и бывает в нейробиологии, одно отдельно взятое исследование не может доказать, что какие-то конкретные нейроны ответственны за определение длительности интервала между звуками.

Аналогичный цепной характер активности нейронов наблюдается и в других отделах мозга. Например, нейроны гипоталамуса крысы возбуждаются в специфические моменты времени в процессе выполнения задачи, такой как бег в колесе или выжидание необходимого времени до выполнения механического действия с целью получения вознаграждения. Интересно, что в разных исследованиях были обнаружены разные цепи активации нейронов в зависимости от конкретных условий. Например, одни и те же нейроны могут возбуждаться в разное время в зависимости от обонятельного стимула, с которого начиналось выполнение задачи. Это означает, что данные нейроны не только отсчитывают абсолютное время, но, как и в примере с гирляндой Элис и Боба, отслеживают время и «запоминают» стимул, вызвавший их активацию.

При выполнении животными различных временны́х задач возникают и гораздо более сложные картины активации нейронов. При работе сложных популяционных часов разные нейроны могут возбуждаться в разные моменты и на разное время, а иногда могут возбуждаться повторно и еще раз через какие-то промежутки времени. Такие пространственно-временны́е картины активации нейронов воспроизводятся в повторных экспериментах, но на первый взгляд могут показаться случайными. В некоторых случаях кажется странным отсутствие понятного ритма или причины подобного поведения. Но в этом-то, возможно, и заключается все дело. Говоря о том, что ритм возбуждения нейронов «случайный», мы подразумеваем, что все нейроны могут возбуждаться и отключаться в тот или иной момент времени практически с равной вероятностью.

Но из теории информации известно, что кодовые системы, в которых все символы или элементы могут использоваться с одинаковой вероятностью, предлагают больше возможностей для хранения или передачи информации. Например, английский язык — не очень эффективный код, поскольку разные буквы используются с очень разной частотой. Печатая текст на английском языке, вы, вполне вероятно, используете клавишу «e» с частотой около 12,5 %, а клавишу «q» не чаще 0,1 %. Сложные и случайные на вид пространственно-временны́е картины возбуждения нейронов могут показаться «некрасивыми», но мозгу они, возможно, предлагают наиболее эффективный способ создания большого числа популяционных часов. Более того, возможно, что сложные режимы активации нейронов в одних областях мозга используются для запуска более простых цепных процессов в других областях.

Вполне вероятно, что даже в диапазоне от сотен миллисекунд до нескольких секунд мозг использует разные механизмы определения времени. У животных, решавших временны́е задачи, были выявлены и другие формы активности нейронов. Возможно, чаще всего встречается механизм активации нейронов, называемый повышением частоты разрядов: как в нижней части песочных часов постепенно увеличивается количество песка, так и количество разрядов («спайков») некоторых нейронов линейно увеличивается со временем. Такая картина обычно наблюдается в тех случаях, когда животных тренируют производить какое-то действие после определенного интервала времени. Но пока мы не знаем, сами ли эти нейроны отсчитывают время, или они считывают показания с других сетей нейронов, чтобы в нужный момент запустить ожидаемый ответ.

До сих пор мы с вами принимали как должное одно важнейшее свойство любых часов — воспроизводимость показаний. Если пространственно-временна́я активность популяции нейронов используется для отсчета времени, она должна воспроизводиться из раза в раз в ответ на одну и ту же ситуацию или один и тот же стимул. В описанных выше экспериментальных исследованиях это условие соблюдалось: каждый раз, когда певчая птица исполняет свою песню, обнаруживается одна и та же нейронная траектория (хотя в каждом исследовании варьируется множество параметров). Однако загадка все еще остается загадкой: как именно мозгу удается вновь и вновь воспроизводить одну и ту же последовательность действий?

Компьютерное моделирование показывает, что схемы активации нейронов в рекуррентных сетях могут постоянно эволюционировать, что теоретически может использоваться для кодирования времени. Проблема заключается в том, что такие эволюционирующие схемы часто не воспроизводятся, а такие сети ведут себя хаотически.

В математике слово «хаос» используется для описания систем, чрезвычайно чувствительных к «шуму» и начальным условиям (состоянию системы в момент начала конкретного эксперимента). Классический пример — погода и так называемый «эффект бабочки», когда самое незначительное событие в какой-то точке пространства и в какой-то момент времени способно вызвать «эффект домино»: например, взмах крыльев бабочки в долине Амазонки в полдень 1 февраля может привести к изменению погоды в Нью-Йорке через неделю.

Хаотические процессы часто наблюдаются в нелинейных физических системах с обратной связью, таких как погода или поведение бильярдных шаров. Сети нейронов обладают обоими этими свойствами. Во-первых, поведение нейронов нелинейно: отклик нейрона не пропорционален полученному им стимулу. Во-вторых, как указывалось выше, кортикальные сети характеризуются высокой степенью рекуррентности: это означает, что активность нейрона в момент времени t₁ влияет на поведение других нейронов в момент времени t₂, что, в свою очередь, влияет на поведение первого нейрона в момент времени t₃.

Чтобы понять, почему хаотические процессы мешают определять время в нелинейных динамических системах, рассмотрим простое математическое уравнение, называемое логистическим уравнением (рис. 6.5). Это уравнение описывает эволюцию параметра x (в пределах от 0 до 1) через определенные временны́е интервалы. На каждой следующей стадии значение параметра x полностью определяется его значением на предыдущей стадии. Несмотря на простоту задачи, результат выглядит достаточно сложно, и минимальные вариации значения x могут вызвать чрезвычайно сильные изменения этого параметра в дальнейшем.

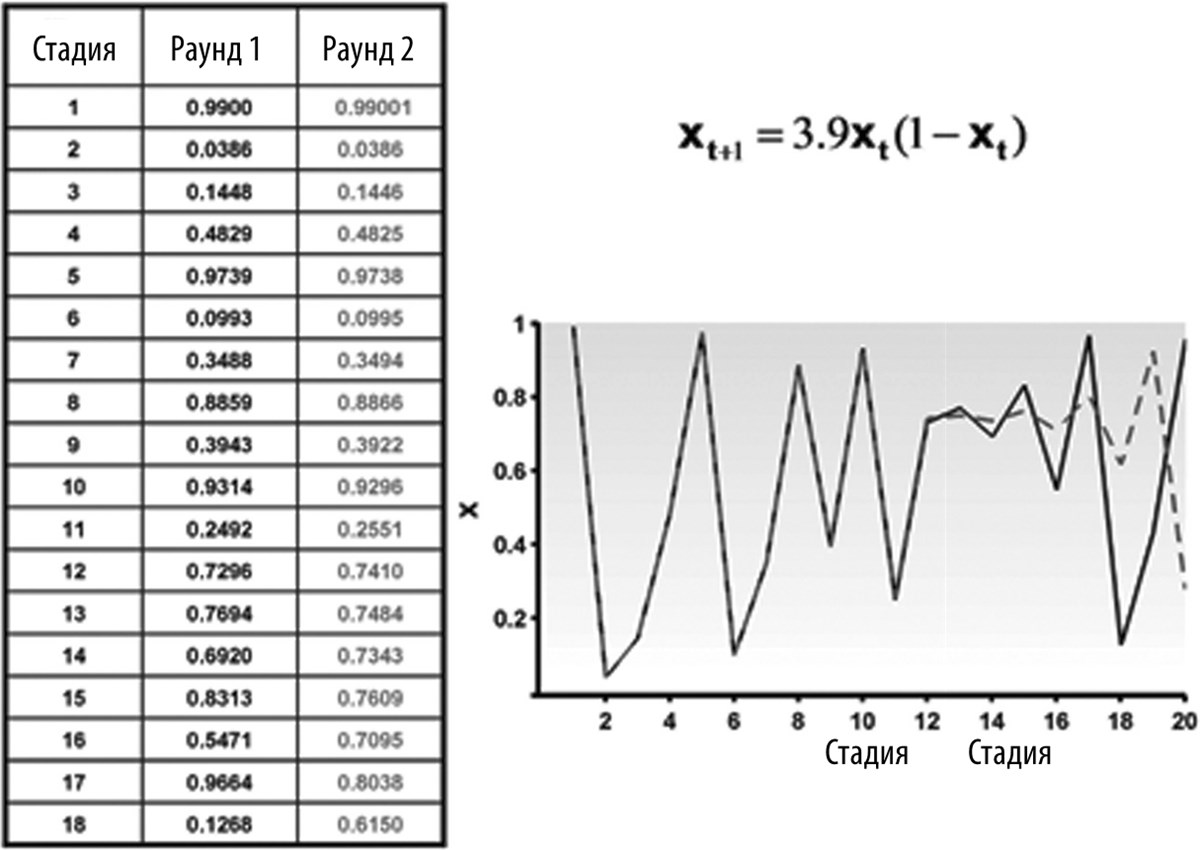
Рис. 6.5. Пример хаотической системы. Значение параметра x на каждой последующей стадии (в момент времени t+1) определяется значением x на текущей стадии. Даже если в двух раундах процесс начинается с очень близких значений x (0,99 и 0,99001), со временем значения x начинают расходиться, что видно из таблицы и из графика. Поначалу это расхождение незаметно, но примерно после 18-й стадии значения x в двух раундах не имеют между собой ничего общего

Заметьте, что представленную на рис. 6.5 таблицу можно использовать в качестве своеобразного таймера. Если известно, что исходное значение x равнялось 0,9900, а текущее значение составляет 0,5471, можно определить, что от начала раунда прошло 16 стадий. Таким образом, в принципе, физические системы, подчиняющиеся такому логистическому уравнению, можно использовать в качестве часов.

Однако проблема заключается в том, что эти системы чрезвычайно чувствительны к помехам или самым незначительным погрешностям измерений. Например, если во втором раунде исходное значение x равно не 0,9900, а 0,99001, на 16-й стадии мы вместо 0,5471 получим 0,7095. Состояние хаотической системы (в данном примере значение параметра x) быстро изменяется в результате самых ничтожных пертурбаций, а это означает, что из раза в раз система ведет себя по-разному. Поэтому хаотические системы — довольно скверные часы.

Компьютерное моделирование систем со случайным распределением связей между нейронами показывает, что такие рекуррентные сети со случайными связями между нейронами могут создавать самовоспроизводящиеся схемы активности, в которых в каждый следующий момент времени сеть находится в ином состоянии. В принципе, такие пространственно-временны́е схемы могут использоваться для определения времени. Однако в 1980-х гг. израильский физик, информатик и нейробиолог Хаим Сомполинский и его коллеги доказали, что во многих случаях такие рекуррентные сети со случайной связью нейронов создают хаотические схемы активности. Это поставило нейробиологов в сложную ситуацию. С одной стороны, кора головного мозга состоит из рекуррентных сетей нейронов, способных создавать воспроизводимые динамические схемы активности — в противном случае мы не могли бы несколько раз сыграть на пианино одну и ту же пьесу или воспроизводить собственную подпись. С другой стороны, теоретические исследования показывают, что кортикальные сети являются хаотическими.

Мы пока еще не знаем, как сети нейронов мозга решают проблему хаоса. Было выдвинуто несколько гипотез, объясняющих способность рекуррентных нейросетей создавать сложные нехаотические образы — такие, которые можно воспроизвести вновь и вновь. Одна модель предполагает, что сети нейронов могут избегать хаоса и воспроизводить специфические траектории возбуждения благодаря обучению синапсов. По крайней мере, в теории, при правильной настройке синапсов в модельной сети нейронов удается получать сложные и нехаотические схемы возбуждения. Как продемонстрировано на рис. 6.6, такой подход является мощным инструментом для создания сложных изменяющихся во времени схем двигательной активности.

Данная модель иллюстрирует характер активности десяти нейронов из сети, состоящей из 800 связанных между собой нейронов, в серии многочисленных испытаний. Каждое испытание начинается с короткого импульса, приводящего все нейроны модельной сети в исходное состояние. Начиная с этой исходной позиции, система изменяется динамическим образом: сеть автономным образом изменяется вдоль траектории, выстроенной в 800-мерном пространстве. Мы наблюдаем упрощенную версию процесса в трехмерном пространстве. Чтобы оценить потенциал данной модельной сети, мы можем соединить все 800 нейронов всего лишь с двумя выходными нейронами и предположить, что эти двигательные нейроны контролируют движение карандаша на листе бумаги относительно осей координат X и Y.

Возможно, это не очень понятно на интуитивном уровне, но если рекуррентная сеть заставляет два двигательных нейрона создавать сложный (точнее, многомерный) динамический образ, то эти выходные нейроны могут создавать практически любой рисунок (что достигается путем настройки силы синапсов между рекуррентной сетью и выходными нейронами). В данном примере два выходных нейрона «написали» слово chaos.

Важно отметить, что рекуррентные связи были соответствующим образом настроены, и поэтому сеть не является хаотической. Можно нарушить активность сети в середине траектории, но она все равно возвращается к тому, что делала раньше. Грубо говоря, эта система обладает памятью. У рекуррентных сетей есть интересное свойство: они способны запоминать свои действия. И даже если сбить систему с исходной траектории, она может «вернуться» и закончить начатую работу.

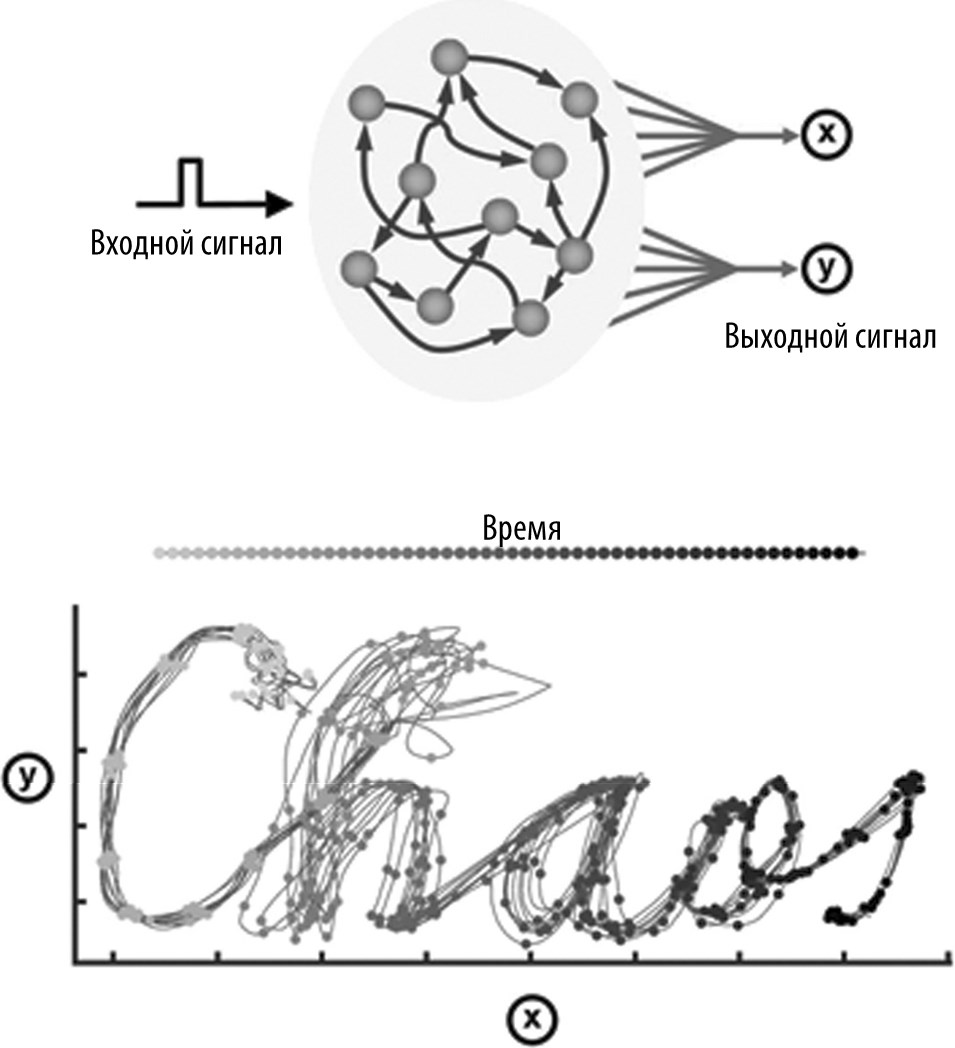
Рис. 6.6. Рекуррентная нейросеть с динамической схемой активности. Данная модельная сеть состоит из взаимосвязанных элементов, имитирующих нейроны (схематично изображено в середине верхней панели). Эти элементы рекуррентной сети получают краткий входной сигнал и передают его двум выходным элементам. Активность этих выходных элементов соответствует положению карандаша по осям X и Y на нижнем графике. Тренировка заключается в настройке весомости связей между элементами сети и выходными элементами в соответствии с правилами обучения. После тренировки в ответ на краткий входной сигнал рекуррентная сеть создает сложную схему активности с такими выходными сигналами, которые заставляют карандаш написать слово «Chaos». Двигательные образы, такие как написанные от руки знаки, являются временны́ми образами, так что данная сеть в каком-то смысле кодирует еще и время. Точки на линиях отмечают время. Эта сеть не является хаотической, поскольку после пертурбаций на подъеме при написании буквы «h» образы воспроизводимо накладываются друг на друга (представлены результаты десяти испытаний). Воспроизводится с модификациями в соответствии со статьей Laje and Buonomano, 2013.

Кроме того, как вы видите, написание слова chaos требует хронометрированного контроля движений, так что движение карандаша можно использовать для определения времени.

Жирные точки на рисунке — это отметки времени: зная текущее положение карандаша, можно определить, сколько времени прошло от момента получения входного сигнала. Таким образом, хаотические рекуррентные сети нейронов можно «приручить» путем настройки силы синаптических связей.

Теперь не помешает на минутку остановиться и задать вопрос: как именно эта нейросеть написала слово «хаос»? (или, точнее, где хранится информация, создающая двумерный образ, который человеческий мозг распознает как слово «хаос»?) Это серьезный вопрос, для ответа на который нужно отвлечься от традиционных представлений о вычислениях и памяти. Информация, на основе которой формируется слово «хаос», одновременно находится повсюду и нигде. В формировании этого образа участвует каждый синапс и каждый активированный нейрон, но ни один конкретный синапс или нейрон не является строго обязательным для формирования образа. Этот образ — эмерджентное свойство системы: общий результат больше суммы составных частей.

Описанная выше сеть — довольно простая компьютерная модель с множеством встроенных допущений. И даже если с ее помощью удается лучше понять какие-то принципы функционирования коры мозга, она слишком проста и негибка, чтобы объяснить удивительную способность мозга обучаться распознавать и создавать такие сложные образы, как речь или музыка. Тем не менее все большее количество экспериментальных данных подтверждает, что многие производимые мозгом вычисления, особенно связанные с отсчетом времени, основаны на способности мозга активизировать в нейросетях сложные динамические траектории, которые могут использоваться для создания пространственно-временны́х образов, лежащих в основе нашей способности быстро пробегать глазами книгу или играть на фортепьяно.

Необходимость отсчитывать время возникает практически во всех решаемых мозгом задачах, причем разные задачи требуют разных способностей: мозгу приходится различать длительность половины и четверти музыкальной ноты, отправлять сообщение с помощью азбуки Морзе, определять время начала озвончения при произнесении согласных звуков «б» или «п» или предугадывать время переключения сигнала светофора. Чтобы решать столь разнообразные задачи, мозг использует набор взаимосвязанных механизмов отсчета времени, распределенных в сетях нейронов. Однако интересно, что часы мозга имеют мало общего с часами, созданными с помощью человеческого мозга.

Сила синапсов со временем изменяется, число возбужденных нейронов увеличивается и уменьшается, частота осцилляций нейронов колеблется, и активность сетей нейронов динамически меняется со временем, поскольку одна из задач, для решения которой эволюционировали нейроны, заключается в определении времени. Так что вопрос, какие именно нейроны или нейросети мозга определяют время, можно сравнить с вопросом, какие именно транзисторы из миллиарда транзисторов в процессоре вашего компьютера отвечают за двоичную логику. В этом процессе участвуют они все, и именно в этом заключается их задача.